27.2.1 相似三角形的判定 第2课时 课件(共26张PPT)
文档属性
| 名称 | 27.2.1 相似三角形的判定 第2课时 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 06:26:17 | ||
图片预览




文档简介
(共26张PPT)
27.2.1相似三角形的判定
---第2课时
人教版
九年级下
教学目标
1.
掌握三角形相似的判定定理二,即三边对应成比例来判定两个三角形相似.(重点)
2.
利用三边对应成比例来判定两个三角形相似的方法进行相关计算.
(重点、难点)
回顾旧知
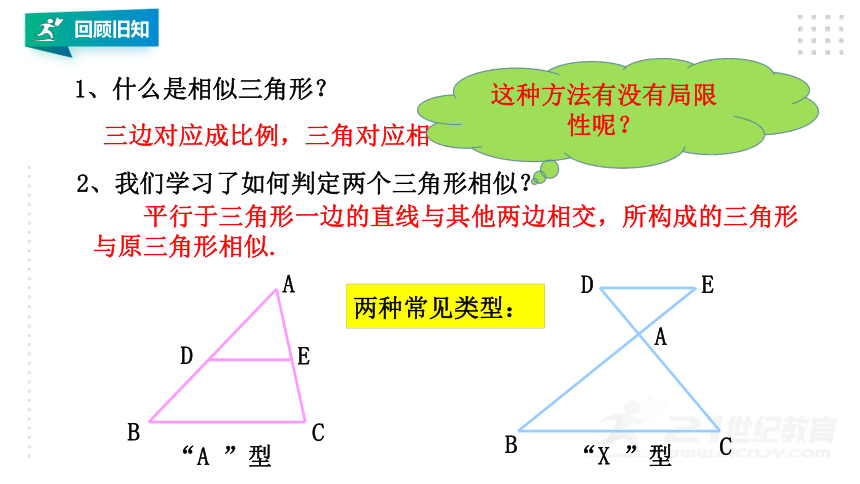
1、什么是相似三角形?
三边对应成比例,三角对应相等的三角形是相似三角形。
2、我们学习了如何判定两个三角形相似?
两种常见类型:
“A
”型
“X
”型
D
E
A
B
C
A
B
C
D
E
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
这种方法有没有局限性呢?
合作探究
我们已经学习了判定两个三角形全等的方法,除了可以验证它们的所有边和角对应相等外,我们还寻求了简便的判定方法,SSS、SAS、ASA、AAS。类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?我们来探究一下!
类似于判定三角形全等的
SSS
方法,我们能不能通
过三边来判定两个三角形相似呢?
合作探究
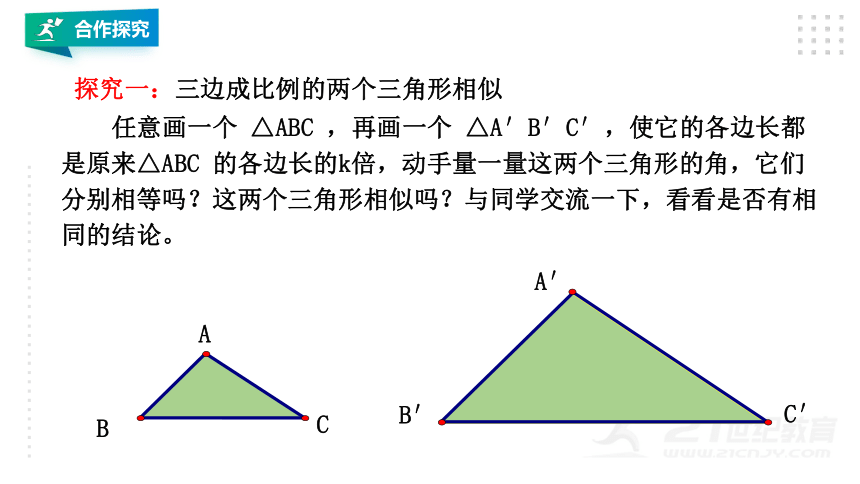
任意画一个
△ABC
,再画一个
△A′B′C′,使它的各边长都是原来△ABC
的各边长的k倍,动手量一量这两个三角形的角,它们分别相等吗?这两个三角形相似吗?与同学交流一下,看看是否有相同的结论。
A′
B′
C′
C
B
A
探究一:三边成比例的两个三角形相似
合作探究
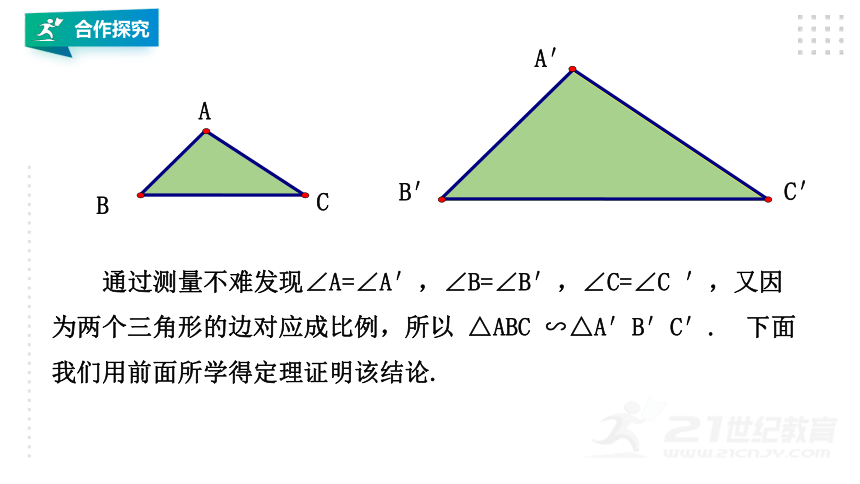
通过测量不难发现∠A=∠A′,∠B=∠B′,∠C=∠C
′,又因为两个三角形的边对应成比例,所以
△ABC
∽△A′B′C′.
下面我们用前面所学得定理证明该结论.
A′
B′
C′
C
B
A
合作探究
∴
C
B
A
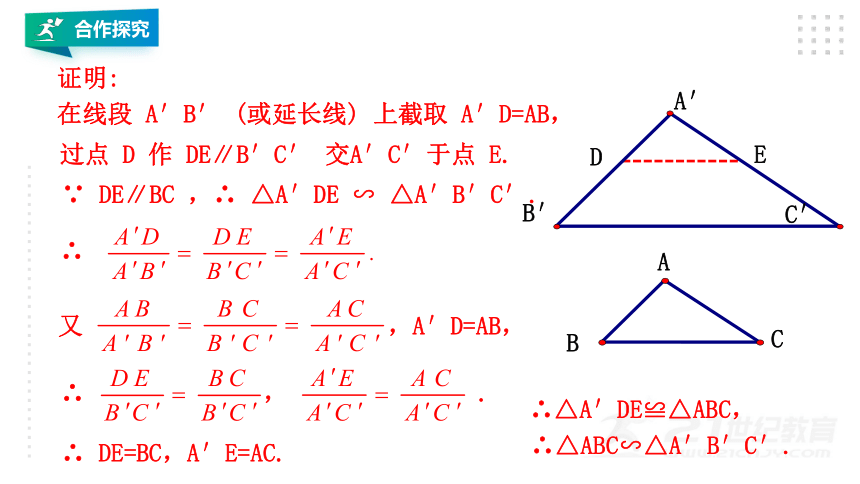
证明:
在线段
A′B′
(或延长线)
上截取
A′D=AB,
过点
D
作
DE∥B′C′
交A′C′于点
E.
∵
DE∥BC
,∴
△A′DE
∽
△A′B′C′.
∴
DE=BC,A′E=AC.
∴△A′DE≌△ABC,
∴△ABC∽△A′B′C′.
B′
C′
A′
D
E
又
,A′D=AB,
∴
,
.
合作探究
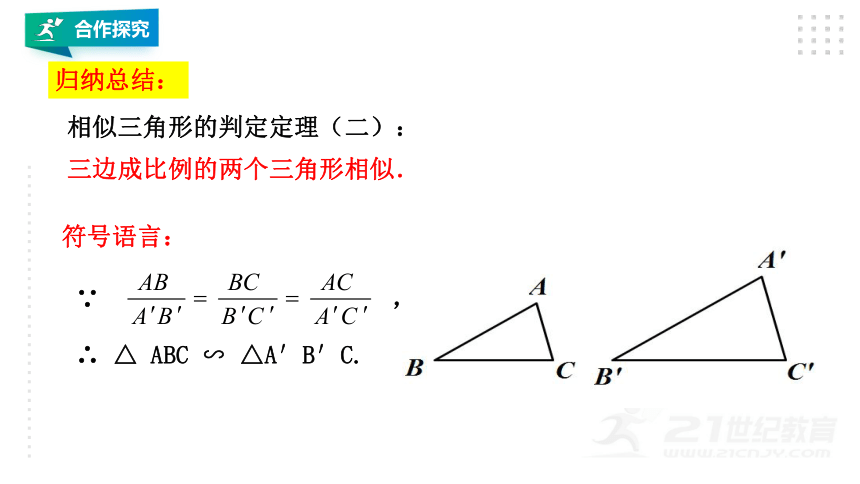
相似三角形的判定定理(二):
三边成比例的两个三角形相似.
归纳总结:
∵
,
∴
△
ABC
∽
△A′B′C.
符号语言:
典例精析
例1
、根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
AB=4
cm
,BC
=6
cm
,AC
=8
cm,
A′B′=12
cm
,B′C′=18
cm
,A′C′=24
cm.
解:相似.理由如下:
∵
∴
∴△ABC∽△A′B′C′.
趁热打铁
1、根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由:AB=
10
cm,BC
=
8
cm,AC
=
16
cm,
A′B′=
16
cm,B′C′=
12.
8
cm,A′C′=
25.
6
cm.
解:相似
知识点拨:这个判定三角形相似的方法与三角形全等的判定方法“边边边”十分相似,所不同的是在相似的判定方法中的
“三边”要求的是“比相等”.
三边的对应关系是“短∶短”“中∶中”“长∶长”.
∴△ABC∽△A′B′C′.
合作探究
归纳总结:
利用三边成比例判定三角形相似的“三步骤”:
(1)排序:将三角形的边按大小顺序排列;
(2)计算:分别计算它们对应边的比值;
(3)判断:通过比值是否相等判断两个三角形是否相似.
趁热打铁
2、图中的两个三角形是否相似?为什么?
相似
理由如下:∵
∴两个三角形的三边成比例.
∴这两个三角形相似.
解:
趁热打铁
3、要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为
4
cm,5
cm和6
cm,另一个三角形框架的一边长为2
cm,它的另外两条边长
应当是多少?你有几种制作方案?
设另外两条边长分别是x
cm和y
cm(x因此另外两条边长应当分别是
cm和3
cm或
cm和
cm或
cm和
cm,即有3种制作方案.
解:
趁热打铁
4、如图,在
Rt△ABC
与
Rt△A′B′C′中,∠C
=∠C
′
=
90°,且
求证:△
A′B′C′∽△ABC.
证明:由已知条件得
AB
=
2
A′B′,AC
=
2
A′C′,
∴
BC
2
=
AB
2-AC
2
=
(
2
A′B′
)2-(
2
A′C′
)2
=
4
A′B′
2-
4
A′C′
2
=
4
(
A′B′
2-A′C′
2
)
=
4
B′C′
2
=
(
2
B′C′
)2.
∴
△
A′B′C′∽△ABC.
∴
BC=2B′C′,
综合演练
1、若△ABC和△A′B′C′满足下列条件,其中使△ABC∽△A′B′C′
的是( )
A.AB=2.5
cm,BC=2
cm,AC=3
cm;
A′B′=3
cm,B′C′=4
cm,A′C′=6
cm
B.AB=2
cm,BC=3
cm,AC=4
cm;
A′B′=3
cm,
B′C′=4.5
cm,A′C′=6
cm
C.AB=10
cm,BC=AC=3
cm;
A′B′=
cm,B′C′=A′C=
cm
D.AB=1
cm,BC=
cm,AC=3
cm;
A′B′=
cm,B′C′=
cm,A′C′=
cm
B
综合演练
2、一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边的长是21,则其他两边长的和是( )
A.19
B.17
C.24
D.21
C
3、若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )
A.增加了10%
B.减少了10%
C.增加了(1+10%)
D.没有改变
D
综合演练
4、图1,图2中小正方形的边长均为1,则图2中的哪一个三角形(阴影部分)与图1中的△ABC相似?
图1
图2
综合演练
解:由勾股定理知AC=
,BC=2,AB=
图2(1)中,三角形的三边长分别为1,
图2
(2)中,三角形的三边长分别为1,
图2
(3)中,三角形的三边长分别为
图2
(4)中,三角形的三边长分别为2,
∴图2
(2)中的三角形与△ABC相似.
综合演练
∴∠BAC=∠DAE,
∴∠BAC
-∠DAC
=
∠DAE
-∠DAC,
即
∠BAD=∠CAE.
∵∠BAD=25°,
∴∠CAE=25°.
∴
△ABC
∽△ADE
(三边成
比例的两个三角形相似).
5、如图,在
△ABC
和
△ADE
中,
,∠BAD=25°,
求∠CAE的度数.
A
B
C
D
E
解:∵
综合演练
6、
如图,∠APD=90°,AP=PB=BC=CD=1,求证:△ABC∽△DBA.
A
C
B
P
D
∵
AB
:
BC
=
BD
:
AB
=
AD
:
AC,
∴△ABC∽△DBA.
证明:
∵∠APD=90°,AP=PB=BC=CD=1,
∴AB=
,AC=
,AD=
.
综合演练
7、如图,△ABC中,点
D,E,F
分别是
AB,BC,CA
的中点,
求证:△ABC∽△EFD.
∴
△ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,
∴
∴
提能训练
8、如图,某地四个乡镇
A,B,C,D
之间建有公路,已知
AB
=
14
千米,AD
=
28
千米,BD
=
21
千米,DC
=
31.5
千米,公路
AB
与
CD
平行吗?说出你的理由.
A
C
B
D
28
14
21
42
31.5
解:公路
AB
与
CD
平行.
∴
∴
△ABD∽△BDC,
∴∠ABD=∠BDC,
∴AB∥DC.
课堂总结
说一说:
1、本节课我们又学习了判定三角形相似的什么方法?
2、需要注意的事项有哪些?
本节课你有哪些收获?
作业布置
习题27.2
P42页:2(1)、6
https://www.21cnjy.com/help/help_extract.php
27.2.1相似三角形的判定
---第2课时
人教版
九年级下
教学目标
1.
掌握三角形相似的判定定理二,即三边对应成比例来判定两个三角形相似.(重点)
2.
利用三边对应成比例来判定两个三角形相似的方法进行相关计算.
(重点、难点)
回顾旧知
1、什么是相似三角形?
三边对应成比例,三角对应相等的三角形是相似三角形。
2、我们学习了如何判定两个三角形相似?
两种常见类型:
“A
”型
“X
”型
D
E
A
B
C
A
B
C
D
E
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
这种方法有没有局限性呢?
合作探究
我们已经学习了判定两个三角形全等的方法,除了可以验证它们的所有边和角对应相等外,我们还寻求了简便的判定方法,SSS、SAS、ASA、AAS。类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?我们来探究一下!
类似于判定三角形全等的
SSS
方法,我们能不能通
过三边来判定两个三角形相似呢?
合作探究
任意画一个
△ABC
,再画一个
△A′B′C′,使它的各边长都是原来△ABC
的各边长的k倍,动手量一量这两个三角形的角,它们分别相等吗?这两个三角形相似吗?与同学交流一下,看看是否有相同的结论。
A′
B′
C′
C
B
A
探究一:三边成比例的两个三角形相似
合作探究
通过测量不难发现∠A=∠A′,∠B=∠B′,∠C=∠C
′,又因为两个三角形的边对应成比例,所以
△ABC
∽△A′B′C′.
下面我们用前面所学得定理证明该结论.
A′
B′
C′
C
B
A
合作探究
∴
C
B
A
证明:
在线段
A′B′
(或延长线)
上截取
A′D=AB,
过点
D
作
DE∥B′C′
交A′C′于点
E.
∵
DE∥BC
,∴
△A′DE
∽
△A′B′C′.
∴
DE=BC,A′E=AC.
∴△A′DE≌△ABC,
∴△ABC∽△A′B′C′.
B′
C′
A′
D
E
又
,A′D=AB,
∴
,
.
合作探究
相似三角形的判定定理(二):
三边成比例的两个三角形相似.
归纳总结:
∵
,
∴
△
ABC
∽
△A′B′C.
符号语言:
典例精析
例1
、根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
AB=4
cm
,BC
=6
cm
,AC
=8
cm,
A′B′=12
cm
,B′C′=18
cm
,A′C′=24
cm.
解:相似.理由如下:
∵
∴
∴△ABC∽△A′B′C′.
趁热打铁
1、根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由:AB=
10
cm,BC
=
8
cm,AC
=
16
cm,
A′B′=
16
cm,B′C′=
12.
8
cm,A′C′=
25.
6
cm.
解:相似
知识点拨:这个判定三角形相似的方法与三角形全等的判定方法“边边边”十分相似,所不同的是在相似的判定方法中的
“三边”要求的是“比相等”.
三边的对应关系是“短∶短”“中∶中”“长∶长”.
∴△ABC∽△A′B′C′.
合作探究
归纳总结:
利用三边成比例判定三角形相似的“三步骤”:
(1)排序:将三角形的边按大小顺序排列;
(2)计算:分别计算它们对应边的比值;
(3)判断:通过比值是否相等判断两个三角形是否相似.
趁热打铁
2、图中的两个三角形是否相似?为什么?
相似
理由如下:∵
∴两个三角形的三边成比例.
∴这两个三角形相似.
解:
趁热打铁
3、要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为
4
cm,5
cm和6
cm,另一个三角形框架的一边长为2
cm,它的另外两条边长
应当是多少?你有几种制作方案?
设另外两条边长分别是x
cm和y
cm(x
cm和3
cm或
cm和
cm或
cm和
cm,即有3种制作方案.
解:
趁热打铁
4、如图,在
Rt△ABC
与
Rt△A′B′C′中,∠C
=∠C
′
=
90°,且
求证:△
A′B′C′∽△ABC.
证明:由已知条件得
AB
=
2
A′B′,AC
=
2
A′C′,
∴
BC
2
=
AB
2-AC
2
=
(
2
A′B′
)2-(
2
A′C′
)2
=
4
A′B′
2-
4
A′C′
2
=
4
(
A′B′
2-A′C′
2
)
=
4
B′C′
2
=
(
2
B′C′
)2.
∴
△
A′B′C′∽△ABC.
∴
BC=2B′C′,
综合演练
1、若△ABC和△A′B′C′满足下列条件,其中使△ABC∽△A′B′C′
的是( )
A.AB=2.5
cm,BC=2
cm,AC=3
cm;
A′B′=3
cm,B′C′=4
cm,A′C′=6
cm
B.AB=2
cm,BC=3
cm,AC=4
cm;
A′B′=3
cm,
B′C′=4.5
cm,A′C′=6
cm
C.AB=10
cm,BC=AC=3
cm;
A′B′=
cm,B′C′=A′C=
cm
D.AB=1
cm,BC=
cm,AC=3
cm;
A′B′=
cm,B′C′=
cm,A′C′=
cm
B
综合演练
2、一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边的长是21,则其他两边长的和是( )
A.19
B.17
C.24
D.21
C
3、若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )
A.增加了10%
B.减少了10%
C.增加了(1+10%)
D.没有改变
D
综合演练
4、图1,图2中小正方形的边长均为1,则图2中的哪一个三角形(阴影部分)与图1中的△ABC相似?
图1
图2
综合演练
解:由勾股定理知AC=
,BC=2,AB=
图2(1)中,三角形的三边长分别为1,
图2
(2)中,三角形的三边长分别为1,
图2
(3)中,三角形的三边长分别为
图2
(4)中,三角形的三边长分别为2,
∴图2
(2)中的三角形与△ABC相似.
综合演练
∴∠BAC=∠DAE,
∴∠BAC
-∠DAC
=
∠DAE
-∠DAC,
即
∠BAD=∠CAE.
∵∠BAD=25°,
∴∠CAE=25°.
∴
△ABC
∽△ADE
(三边成
比例的两个三角形相似).
5、如图,在
△ABC
和
△ADE
中,
,∠BAD=25°,
求∠CAE的度数.
A
B
C
D
E
解:∵
综合演练
6、
如图,∠APD=90°,AP=PB=BC=CD=1,求证:△ABC∽△DBA.
A
C
B
P
D
∵
AB
:
BC
=
BD
:
AB
=
AD
:
AC,
∴△ABC∽△DBA.
证明:
∵∠APD=90°,AP=PB=BC=CD=1,
∴AB=
,AC=
,AD=
.
综合演练
7、如图,△ABC中,点
D,E,F
分别是
AB,BC,CA
的中点,
求证:△ABC∽△EFD.
∴
△ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,
∴
∴
提能训练
8、如图,某地四个乡镇
A,B,C,D
之间建有公路,已知
AB
=
14
千米,AD
=
28
千米,BD
=
21
千米,DC
=
31.5
千米,公路
AB
与
CD
平行吗?说出你的理由.
A
C
B
D
28
14
21
42
31.5
解:公路
AB
与
CD
平行.
∴
∴
△ABD∽△BDC,
∴∠ABD=∠BDC,
∴AB∥DC.
课堂总结
说一说:
1、本节课我们又学习了判定三角形相似的什么方法?
2、需要注意的事项有哪些?
本节课你有哪些收获?
作业布置
习题27.2
P42页:2(1)、6
https://www.21cnjy.com/help/help_extract.php
