2021-2022学年人教版数学九年级上册24.4.1 弧长和扇形面积 课件(35张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.4.1 弧长和扇形面积 课件(35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 634.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 16:57:44 | ||
图片预览






文档简介
(共35张PPT)
24.4.1弧长和扇形面积
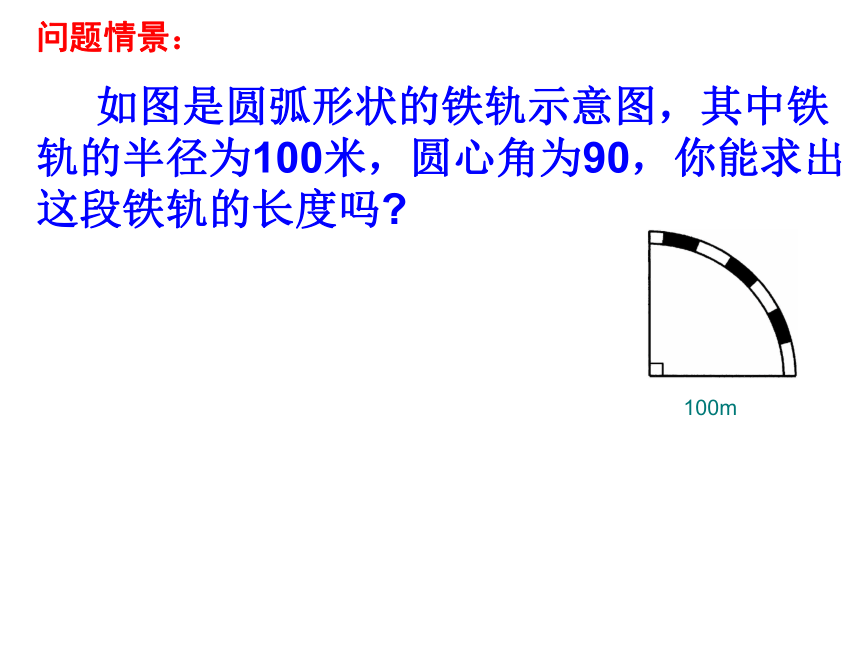
如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90,你能求出这段铁轨的长度吗?
问题情景:
100m
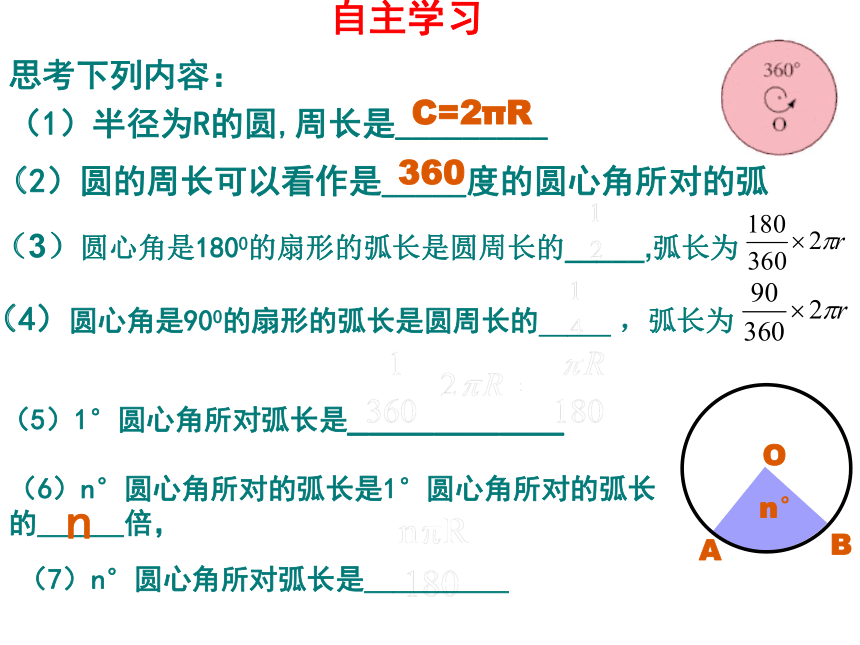
(1)半径为R的圆,周长是_________
C=2πR
A
B
O
n°
(6)n°圆心角所对的弧长是1°圆心角所对的弧长的______倍,
n
(7)n°圆心角所对弧长是__________
自主学习
思考下列内容:
(2)圆的周长可以看作是_____度的圆心角所对的弧
360
(5)1°圆心角所对弧长是__________
(3)圆心角是1800的扇形的弧长是圆周长的_____,弧长为
(4)圆心角是900的扇形的弧长是圆周长的_____
,弧长为
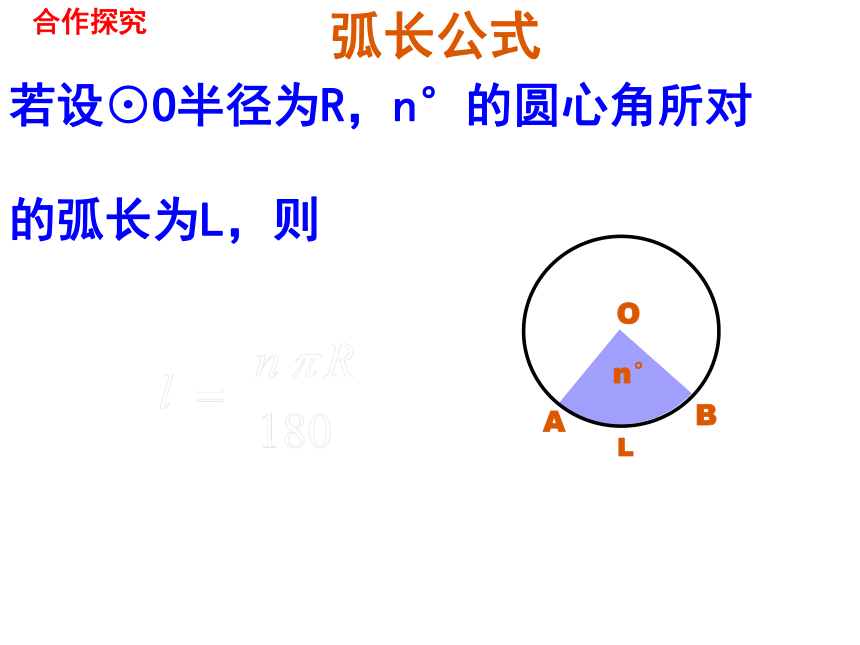
弧长公式
若设⊙O半径为R,n°的圆心角所对
的弧长为L,则
L
A
B
O
n°
合作探究
(1)已知圆的半径为10cm,半圆的弧长为(
)
(2)已知圆的半径为9cm
,60°圆心角所对的弧长为(
)
(3)已知半径为3,则弧长为π的弧所对的圆心角为_______
(4)已知圆心角为150°,所对的弧长为20π,则圆的半径为_______。
10πcm
600
24
牛刀小试
3πcm
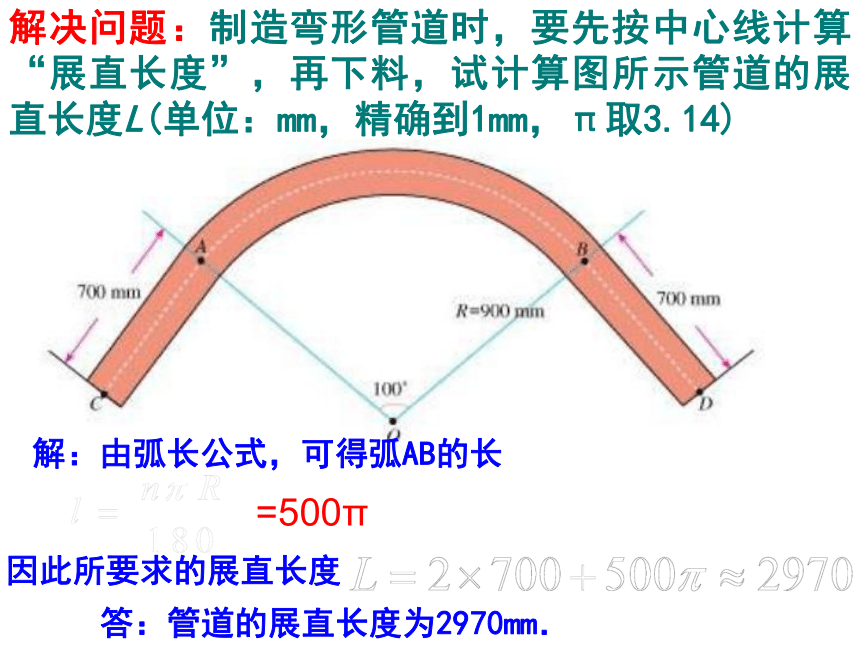
例1:制造弯形管道时,要先按中心线计算“展直长度”(中心虚线的长度),再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
实际应用
合作探究
解决问题:制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm,π取3.14)
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
答:管道的展直长度为2970mm.
=500π
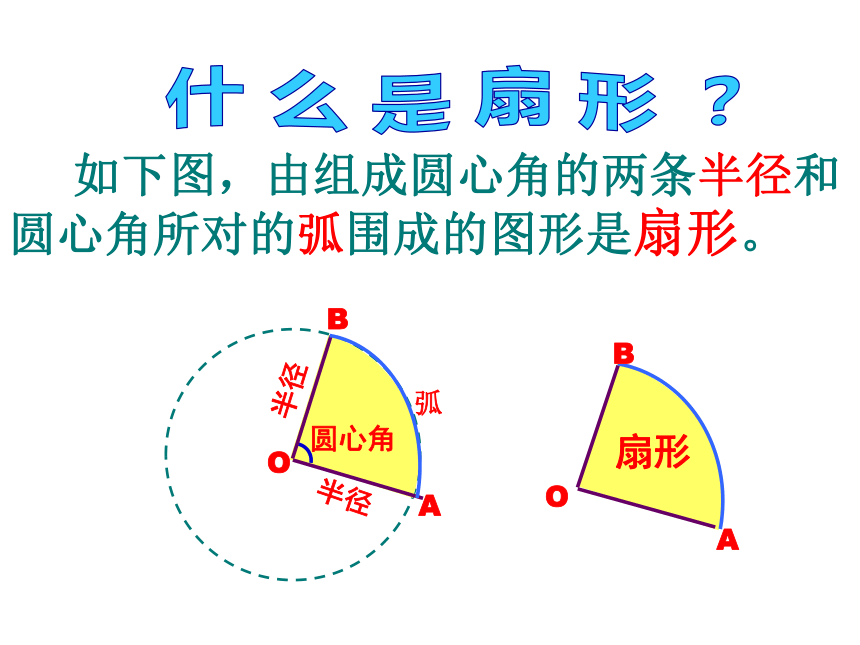
什
么
是
扇
形
?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
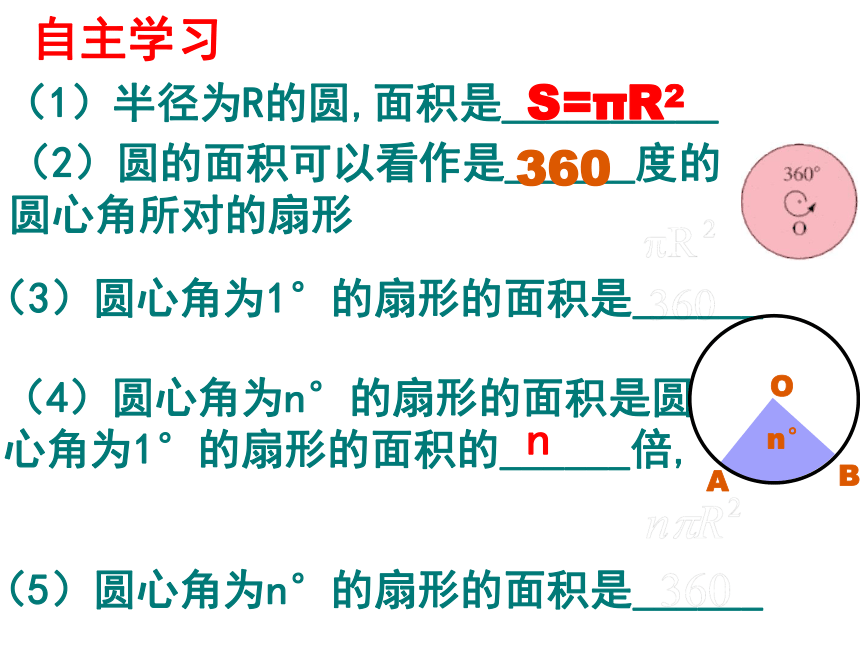
(1)半径为R的圆,面积是__________
S=πR2
(3)圆心角为1°的扇形的面积是______
(4)圆心角为n°的扇形的面积是圆
心角为1°的扇形的面积的______倍,
n
(5)圆心角为n°的扇形的面积是______
自主学习
A
B
O
n°
(2)圆的面积可以看作是______度的圆心角所对的扇形
360
扇形面积公式
若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形,则
已知扇形的圆心角为120°,半径为2,则这个扇形的面积为多少?
练习1
已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2,
练习2
问题:扇形的弧长公式与面积公式有联系吗?
自主探究
公式2:
已知扇形的半径为3cm,扇形的弧长为
πcm,则该扇形的面积是______cm2,
回顾思考
综合应用
1.如图,扇形纸扇完全打开后,外侧两竹条AB、AC夹角为120°,AB的长为30cm,贴纸部分BD的长为20cm,求贴纸部分的面积.
解:
2.在圆O中,圆心O到弦AB的距离等于弦长的
一半,该弦所对的弧长是47πcm,求圆O的半径。
例2:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。
0
B
A
C
D
弓形的面积
=
S扇-
S⊿AOB
变式:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。(精确到0.01cm)。
0
A
B
D
C
E
弓形的面积
=
S扇+
S△
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
规律提升
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
如图是一段弯型管道,其中∠O=∠O‘=90?,中心线的两条圆弧半径都为1000mm,求图中管道的展直长度(π取3.142).p115
试试你能行
试一试
例2:如图,在△AOC中,∠AOC=900,∠C=150,以O为圆心,AO为半径的圆交AC于B点,若OA=6,
求弧AB的长。
A
C
B
O
8.
(2006,武汉)如图,⊙A、⊙B、⊙C、⊙D它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的弧长之和是
点击中考
2π
想一想
no
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的一端栓着一只狗。
(1)这只狗的活动范围是个什么图形?
(2)这只狗的最大活动区域有多大?
(3)如果这只狗只能绕柱子转过n度的角,那么它的最大活动区域有多大?
9πm2
1、已知扇形的圆心角为120°,半径为2,
则这个扇形的面积S扇形=_
.
练习
2、已知扇形面积为
,圆心角为60°,则
这个扇形的半径
R=____.
3、已知半径为2cm的扇形,其弧长为
,则这个扇形的面积是(
).
4、(2007,四川内江)如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为1200,OC长为8cm,CA长为12cm,则贴纸部分的面积为(
)
A.
B.
C.
D.
练习
(1)已知圆的半径为10cm,半圆的弧长为(
)
(2)已知圆的半径为9cm
,60°圆心角所对的弧长为(
)
(3)已知半径为3,则弧长为π的弧所对的圆心角为_______
(4)已知圆心角为150°,所对的弧长为20π,则圆的半径为_______。
10πcm
600
24
牛刀小试
3πcm
试一试
例2:如图,在△AOC中,∠AOC=900,∠C=150,以O为圆心,AO为半径的圆交AC于B点,若OA=6,
求弧AB的长。
A
C
B
O
将以边长为1的等边三角形木板沿水平线翻滚(如图所示),那么点B从开始至结束所经过的路径的长度为____。
试一试
变式:边长为2的正方形木块在水平地面上翻滚两周(如图所示)后,顶点A所经过的路径总长为_______。
8.
(2006,武汉)如图,⊙A、⊙B、⊙C、⊙D它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的弧长之和是
点击中考
2π
通过本节课的学习,
我知道了……
学到了……感受到了……
体会分享
自我小结
:
2.
扇形面积公式与弧长公式的区别:
S扇形=
S圆
360
n
l弧=
C圆
360
n
1.扇形的弧长和面积大小与哪些因素有关?
(2)与半径的长短有关
(1)与圆心角的大小有关
再见
24.4.1弧长和扇形面积
如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90,你能求出这段铁轨的长度吗?
问题情景:
100m
(1)半径为R的圆,周长是_________
C=2πR
A
B
O
n°
(6)n°圆心角所对的弧长是1°圆心角所对的弧长的______倍,
n
(7)n°圆心角所对弧长是__________
自主学习
思考下列内容:
(2)圆的周长可以看作是_____度的圆心角所对的弧
360
(5)1°圆心角所对弧长是__________
(3)圆心角是1800的扇形的弧长是圆周长的_____,弧长为
(4)圆心角是900的扇形的弧长是圆周长的_____
,弧长为
弧长公式
若设⊙O半径为R,n°的圆心角所对
的弧长为L,则
L
A
B
O
n°
合作探究
(1)已知圆的半径为10cm,半圆的弧长为(
)
(2)已知圆的半径为9cm
,60°圆心角所对的弧长为(
)
(3)已知半径为3,则弧长为π的弧所对的圆心角为_______
(4)已知圆心角为150°,所对的弧长为20π,则圆的半径为_______。
10πcm
600
24
牛刀小试
3πcm
例1:制造弯形管道时,要先按中心线计算“展直长度”(中心虚线的长度),再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
实际应用
合作探究
解决问题:制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm,π取3.14)
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
答:管道的展直长度为2970mm.
=500π
什
么
是
扇
形
?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
(1)半径为R的圆,面积是__________
S=πR2
(3)圆心角为1°的扇形的面积是______
(4)圆心角为n°的扇形的面积是圆
心角为1°的扇形的面积的______倍,
n
(5)圆心角为n°的扇形的面积是______
自主学习
A
B
O
n°
(2)圆的面积可以看作是______度的圆心角所对的扇形
360
扇形面积公式
若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形,则
已知扇形的圆心角为120°,半径为2,则这个扇形的面积为多少?
练习1
已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2,
练习2
问题:扇形的弧长公式与面积公式有联系吗?
自主探究
公式2:
已知扇形的半径为3cm,扇形的弧长为
πcm,则该扇形的面积是______cm2,
回顾思考
综合应用
1.如图,扇形纸扇完全打开后,外侧两竹条AB、AC夹角为120°,AB的长为30cm,贴纸部分BD的长为20cm,求贴纸部分的面积.
解:
2.在圆O中,圆心O到弦AB的距离等于弦长的
一半,该弦所对的弧长是47πcm,求圆O的半径。
例2:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。
0
B
A
C
D
弓形的面积
=
S扇-
S⊿AOB
变式:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。(精确到0.01cm)。
0
A
B
D
C
E
弓形的面积
=
S扇+
S△
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
规律提升
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
如图是一段弯型管道,其中∠O=∠O‘=90?,中心线的两条圆弧半径都为1000mm,求图中管道的展直长度(π取3.142).p115
试试你能行
试一试
例2:如图,在△AOC中,∠AOC=900,∠C=150,以O为圆心,AO为半径的圆交AC于B点,若OA=6,
求弧AB的长。
A
C
B
O
8.
(2006,武汉)如图,⊙A、⊙B、⊙C、⊙D它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的弧长之和是
点击中考
2π
想一想
no
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的一端栓着一只狗。
(1)这只狗的活动范围是个什么图形?
(2)这只狗的最大活动区域有多大?
(3)如果这只狗只能绕柱子转过n度的角,那么它的最大活动区域有多大?
9πm2
1、已知扇形的圆心角为120°,半径为2,
则这个扇形的面积S扇形=_
.
练习
2、已知扇形面积为
,圆心角为60°,则
这个扇形的半径
R=____.
3、已知半径为2cm的扇形,其弧长为
,则这个扇形的面积是(
).
4、(2007,四川内江)如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为1200,OC长为8cm,CA长为12cm,则贴纸部分的面积为(
)
A.
B.
C.
D.
练习
(1)已知圆的半径为10cm,半圆的弧长为(
)
(2)已知圆的半径为9cm
,60°圆心角所对的弧长为(
)
(3)已知半径为3,则弧长为π的弧所对的圆心角为_______
(4)已知圆心角为150°,所对的弧长为20π,则圆的半径为_______。
10πcm
600
24
牛刀小试
3πcm
试一试
例2:如图,在△AOC中,∠AOC=900,∠C=150,以O为圆心,AO为半径的圆交AC于B点,若OA=6,
求弧AB的长。
A
C
B
O
将以边长为1的等边三角形木板沿水平线翻滚(如图所示),那么点B从开始至结束所经过的路径的长度为____。
试一试
变式:边长为2的正方形木块在水平地面上翻滚两周(如图所示)后,顶点A所经过的路径总长为_______。
8.
(2006,武汉)如图,⊙A、⊙B、⊙C、⊙D它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的弧长之和是
点击中考
2π
通过本节课的学习,
我知道了……
学到了……感受到了……
体会分享
自我小结
:
2.
扇形面积公式与弧长公式的区别:
S扇形=
S圆
360
n
l弧=
C圆
360
n
1.扇形的弧长和面积大小与哪些因素有关?
(2)与半径的长短有关
(1)与圆心角的大小有关
再见
同课章节目录
