25.1随机事件与概率 同步练习(含解析)
文档属性
| 名称 | 25.1随机事件与概率 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 225.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 20:17:18 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
25.1随机事件与概率
一、选择题
下列事件中,属于必然事件的是
A.三角形的外心到三边的距离相等
B.某射击运动员射击一次,命中靶心
C.任意画一个三角形,其内角和是
D.抛一枚硬币,落地后正面朝上
下列事件中,是必然事件的是
A.我市夏季的平均气温比冬季的平均气温高.
B.掷一枚均匀硬币,正面一定朝上.
C.打开电视机,正在播放动画片.
D.每周的星期日一定是晴天.
如图,
过矩形
对角线的交点
,且分别交
,
于点
,,矩形
内的一个动点
落在阴影部分的概率是
A.
B.
C.
D.
下列事件:①阴天会下雨;②随机掷一枚均匀的硬币,正面朝上;③
名同学中,有两人的出生月份相同;④济南是山东省的省会.其中不确定事件有
A.
个
B.
个
C.
个
D.
个
一枚质地均匀的骰子,其六个面上分别标有数字
,,,,,,投掷一次,朝上一面的数字是偶数的概率为
A.
B.
C.
D.
在
张形状相同的卡片上,分别写有下列
个命题:
①同位角相等;
②三角形中至少有两个锐角;
③三角形三个外角的和是
;
④三角形中至少有一个角大于
;
⑤如果两条直线平行,那么同旁内角的平分线互相垂直.
从中任意抽取一张卡片,抽取到卡片写有真命题的概率是
A.
B.
C.
D.
二、填空题
某小区共有学生
人,随机抽查
名学生,其中有
人看中央电视台的晚间新闻.在该小区随便问一位学生,他看中央电视台晚间新闻的概率大约是
.
如图,在边长为
的正方形内有一边长为
的小正方形,一只青蛙在该图案内任意跳动,则这只青蛙跳入阴影部分的概率是
.
有三张外观完全相同的卡片,在卡片的正面分别标上数字
,,,将正面朝下放在桌面上,现随机翻开一张卡片,则卡片上的数字为负数的概率为
.
定义一种新运算
,例如
.按照这种运算规定,已知
,当
从
,,,,
这五个数中取值,使得
成立的概率为
.
有
根细木棒,长度分别为
,,,,从中任选
根,恰好能搭成一个三角形的概率是
.
三、解答题
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有
名学生参加决赛,这
名学生同时默写
首古诗词,若每正确默写出一首古诗词得
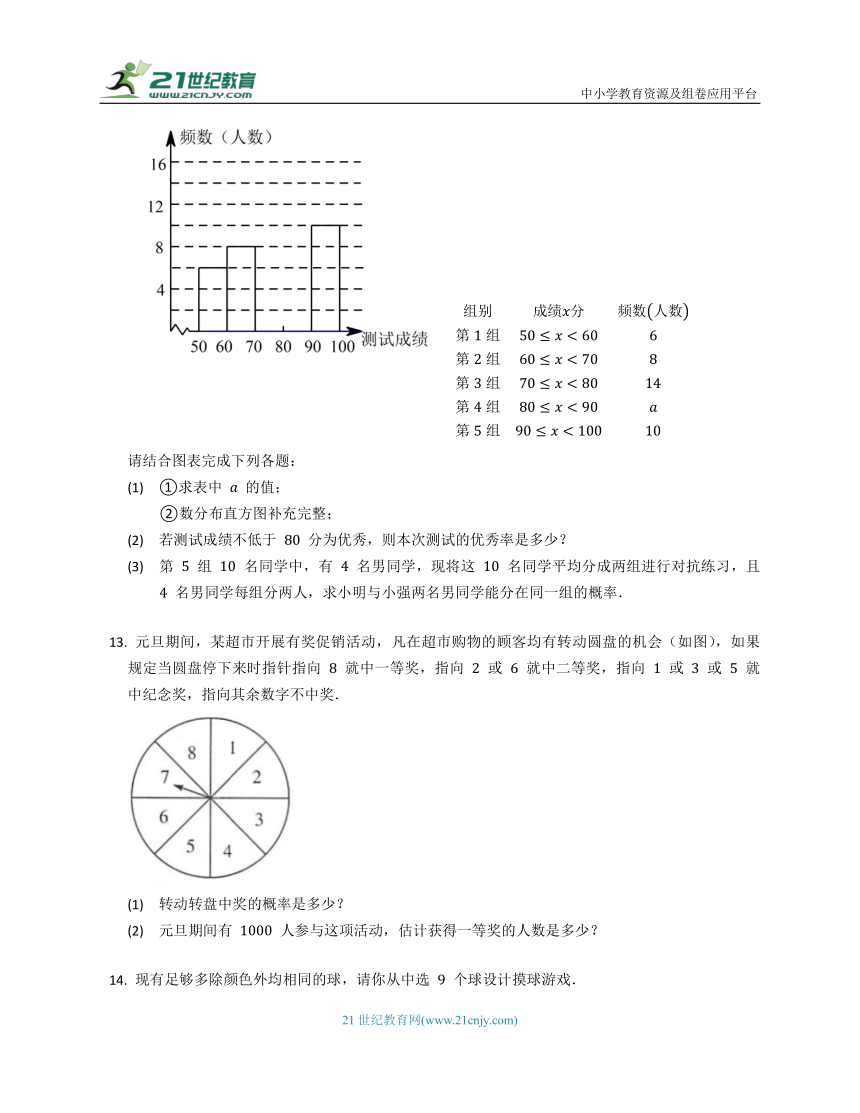
分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)
①求表中
的值;
②数分布直方图补充完整;
(2)
若测试成绩不低于
分为优秀,则本次测试的优秀率是多少?
(3)
第
组
名同学中,有
名男同学,现将这
名同学平均分成两组进行对抗练习,且
名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
元旦期间,某超市开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向
就中一等奖,指向
或
就中二等奖,指向
或
或
就中纪念奖,指向其余数字不中奖.
(1)
转动转盘中奖的概率是多少?
(2)
元旦期间有
人参与这项活动,估计获得一等奖的人数是多少?
现有足够多除颜色外均相同的球,请你从中选
个球设计摸球游戏.
(1)
使摸到红球的概率和摸到白球的概率相等.
(2)
使摸到红球、白球、黑球的概率都相等.
(3)
使摸到红球的概率和摸到白球的概率相等,且都小于摸到黑球的概率.
某路口南北方向红绿灯的设置时间为:红灯
、绿灯
、黄灯
.司机
随机地由南往北开车到达该路口,问:
(1)
他遇到红灯的概率大还是遇到绿灯的概率大?
(2)
他遇到绿灯的概率是多少?
答案
一、选择题
1.
【答案】C
【知识点】事件的分类
2.
【答案】A
【知识点】事件的分类
3.
【答案】B
【知识点】公式求概率
4.
【答案】C
【解析】①阴天会下雨;
②随机掷一枚均匀的硬币,正面朝上;
③
名同学中,有两人的出生月份相同;均为不确定事件;
④济南是山东省的省会为确定事件;
不确定事件有
个.
【知识点】事件的分类
5.
【答案】C
【解析】
一枚质地均匀的骰子,其六个面上分别标有数字
,,,,,,投掷一次,
朝上一面的数字是偶数的概率为:.
【知识点】公式求概率
6.
【答案】B
【解析】同位角不一定相等,①是假命题;
三角形中至少有两个锐角,②是真命题;
三角形三个外角的和是
,③是真命题;
三角形中至少有一个角大于
,④是假命题;
如果两条直线平行,那么同旁内角的平分线互相垂直,⑤是真命题.
五个命题中,真命题的个数是
,则从中任意抽取一张卡片,抽取到卡片写有真命题的概率是
.
【知识点】公式求概率
二、填空题
7.
【答案】
【知识点】公式求概率
8.
【答案】
【解析】求解得图形中空白的面积:,正方形的面积为
,得出阴影部分的面积为:,运用几何概率公式求解即可.
这只青蛙跳入阴影部分的概率等于阴影部分面积与总面积的比是:.
【知识点】公式求概率
9.
【答案】
【知识点】公式求概率
10.
【答案】
【解析】由题意可知:,
,
,
,
解得:
或
,
从
,,,,
这五个数中取值,使得
成立的概率为
.
【知识点】公式求概率
11.
【答案】
【解析】根据题意,从
根细木棒中任取
根,有
,,;,,;,,;,,,共
种取法,
而能搭成一个三角形的有种
,,;,,;,,,
种.
【知识点】公式求概率
三、解答题
12.
【答案】
(1)
①由题意和表格,可得
,
即
的值是
.
②补充完整的频数分布直方图如下图所示.
(2)
测试成绩不低于
分为优秀,
本次测试的优秀率是:.
(3)
设小明和小强分别为
,,另外两名学生为:,,
则所有的可能性为
小明和小强分在一起的概率为:.
【知识点】公式求概率、频数分布表及直方图
13.
【答案】
(1)
指针指向
,,,,,
都获奖,
获奖概率
.
(2)
获得一等奖的概率为
,
(人),
获得一等奖的人数可能是
人.
【知识点】用样本估算总体、公式求概率
14.
【答案】
(1)
个球中,有
个红球,
个白球,
个黑球可使摸到红球的概率和摸到白球的概率相等.
(2)
个球中,有
个红球,
个白球,
个黑球可使摸到红球、白球、黑球的概率都相等.
(3)
个球中,有
个红球,
个白球,
个黑球可使摸到红球的概率和摸到白球的概率相等,且都小于摸到黑球的概率.
【知识点】公式求概率
15.
【答案】
(1)
红灯
、绿灯
、黄灯
,
他遇到绿灯的概率大.
(2)
遇到绿灯的概率
,
故遇到绿灯的概率是
.
【知识点】公式求概率、概率的概念及意义
21世纪教育网(www.21cnjy.com)
25.1随机事件与概率
一、选择题
下列事件中,属于必然事件的是
A.三角形的外心到三边的距离相等
B.某射击运动员射击一次,命中靶心
C.任意画一个三角形,其内角和是
D.抛一枚硬币,落地后正面朝上
下列事件中,是必然事件的是
A.我市夏季的平均气温比冬季的平均气温高.
B.掷一枚均匀硬币,正面一定朝上.
C.打开电视机,正在播放动画片.
D.每周的星期日一定是晴天.
如图,
过矩形
对角线的交点
,且分别交
,
于点
,,矩形
内的一个动点
落在阴影部分的概率是
A.
B.
C.
D.
下列事件:①阴天会下雨;②随机掷一枚均匀的硬币,正面朝上;③
名同学中,有两人的出生月份相同;④济南是山东省的省会.其中不确定事件有
A.
个
B.
个
C.
个
D.
个
一枚质地均匀的骰子,其六个面上分别标有数字
,,,,,,投掷一次,朝上一面的数字是偶数的概率为
A.
B.
C.
D.
在
张形状相同的卡片上,分别写有下列
个命题:
①同位角相等;
②三角形中至少有两个锐角;
③三角形三个外角的和是
;
④三角形中至少有一个角大于
;
⑤如果两条直线平行,那么同旁内角的平分线互相垂直.
从中任意抽取一张卡片,抽取到卡片写有真命题的概率是
A.
B.
C.
D.
二、填空题
某小区共有学生
人,随机抽查
名学生,其中有
人看中央电视台的晚间新闻.在该小区随便问一位学生,他看中央电视台晚间新闻的概率大约是
.
如图,在边长为
的正方形内有一边长为
的小正方形,一只青蛙在该图案内任意跳动,则这只青蛙跳入阴影部分的概率是
.
有三张外观完全相同的卡片,在卡片的正面分别标上数字
,,,将正面朝下放在桌面上,现随机翻开一张卡片,则卡片上的数字为负数的概率为
.
定义一种新运算
,例如
.按照这种运算规定,已知
,当
从
,,,,
这五个数中取值,使得
成立的概率为
.
有
根细木棒,长度分别为
,,,,从中任选
根,恰好能搭成一个三角形的概率是
.
三、解答题
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有
名学生参加决赛,这
名学生同时默写
首古诗词,若每正确默写出一首古诗词得
分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)
①求表中
的值;
②数分布直方图补充完整;
(2)
若测试成绩不低于
分为优秀,则本次测试的优秀率是多少?
(3)
第
组
名同学中,有
名男同学,现将这
名同学平均分成两组进行对抗练习,且
名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
元旦期间,某超市开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向
就中一等奖,指向
或
就中二等奖,指向
或
或
就中纪念奖,指向其余数字不中奖.
(1)
转动转盘中奖的概率是多少?
(2)
元旦期间有
人参与这项活动,估计获得一等奖的人数是多少?
现有足够多除颜色外均相同的球,请你从中选
个球设计摸球游戏.
(1)
使摸到红球的概率和摸到白球的概率相等.
(2)
使摸到红球、白球、黑球的概率都相等.
(3)
使摸到红球的概率和摸到白球的概率相等,且都小于摸到黑球的概率.
某路口南北方向红绿灯的设置时间为:红灯
、绿灯
、黄灯
.司机
随机地由南往北开车到达该路口,问:
(1)
他遇到红灯的概率大还是遇到绿灯的概率大?
(2)
他遇到绿灯的概率是多少?
答案
一、选择题
1.
【答案】C
【知识点】事件的分类
2.
【答案】A
【知识点】事件的分类
3.
【答案】B
【知识点】公式求概率
4.
【答案】C
【解析】①阴天会下雨;
②随机掷一枚均匀的硬币,正面朝上;
③
名同学中,有两人的出生月份相同;均为不确定事件;
④济南是山东省的省会为确定事件;
不确定事件有
个.
【知识点】事件的分类
5.
【答案】C
【解析】
一枚质地均匀的骰子,其六个面上分别标有数字
,,,,,,投掷一次,
朝上一面的数字是偶数的概率为:.
【知识点】公式求概率
6.
【答案】B
【解析】同位角不一定相等,①是假命题;
三角形中至少有两个锐角,②是真命题;
三角形三个外角的和是
,③是真命题;
三角形中至少有一个角大于
,④是假命题;
如果两条直线平行,那么同旁内角的平分线互相垂直,⑤是真命题.
五个命题中,真命题的个数是
,则从中任意抽取一张卡片,抽取到卡片写有真命题的概率是
.
【知识点】公式求概率
二、填空题
7.
【答案】
【知识点】公式求概率
8.
【答案】
【解析】求解得图形中空白的面积:,正方形的面积为
,得出阴影部分的面积为:,运用几何概率公式求解即可.
这只青蛙跳入阴影部分的概率等于阴影部分面积与总面积的比是:.
【知识点】公式求概率
9.
【答案】
【知识点】公式求概率
10.
【答案】
【解析】由题意可知:,
,
,
,
解得:
或
,
从
,,,,
这五个数中取值,使得
成立的概率为
.
【知识点】公式求概率
11.
【答案】
【解析】根据题意,从
根细木棒中任取
根,有
,,;,,;,,;,,,共
种取法,
而能搭成一个三角形的有种
,,;,,;,,,
种.
【知识点】公式求概率
三、解答题
12.
【答案】
(1)
①由题意和表格,可得
,
即
的值是
.
②补充完整的频数分布直方图如下图所示.
(2)
测试成绩不低于
分为优秀,
本次测试的优秀率是:.
(3)
设小明和小强分别为
,,另外两名学生为:,,
则所有的可能性为
小明和小强分在一起的概率为:.
【知识点】公式求概率、频数分布表及直方图
13.
【答案】
(1)
指针指向
,,,,,
都获奖,
获奖概率
.
(2)
获得一等奖的概率为
,
(人),
获得一等奖的人数可能是
人.
【知识点】用样本估算总体、公式求概率
14.
【答案】
(1)
个球中,有
个红球,
个白球,
个黑球可使摸到红球的概率和摸到白球的概率相等.
(2)
个球中,有
个红球,
个白球,
个黑球可使摸到红球、白球、黑球的概率都相等.
(3)
个球中,有
个红球,
个白球,
个黑球可使摸到红球的概率和摸到白球的概率相等,且都小于摸到黑球的概率.
【知识点】公式求概率
15.
【答案】
(1)
红灯
、绿灯
、黄灯
,
他遇到绿灯的概率大.
(2)
遇到绿灯的概率
,
故遇到绿灯的概率是
.
【知识点】公式求概率、概率的概念及意义
21世纪教育网(www.21cnjy.com)
同课章节目录
