冀教版数学九年级上册25.7相似多边形和图形的位似 课件(26张PPT)
文档属性
| 名称 | 冀教版数学九年级上册25.7相似多边形和图形的位似 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 320.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
25.7相似多边形和图形的位似
1.理解相似图形的定义并能判断两图形是否相似。
2.学习并掌握相似多边形的性质与判定方法。(重点、难点)
3.理解并掌握位似图形的相关概念。
4.学习并掌握位似图形的性质并能够运用其解决问题。(重点)
学习目标
问题1
请观察下面几组图片,它们有何共同之处?
观察与思考
相同点:形状相同。
不同点:大小不相同。
相似图形的概念:
形状相同的图形叫做相似图形。
注意:相似图形的大小不一定相同。
归纳
相似多边形的性质
二
图中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系?
由此可以得到两个相似多边形的性质:
实际上这也是我们判定两个多边形是否相似的方法,即如果_______
_______
___
____,
那么这两个多边形相似。
对应边成比例,对应角相等
对应边成比例,对应角相等。
相似多边形的判定
三
A
B
C
A1
B1
C1
缩小
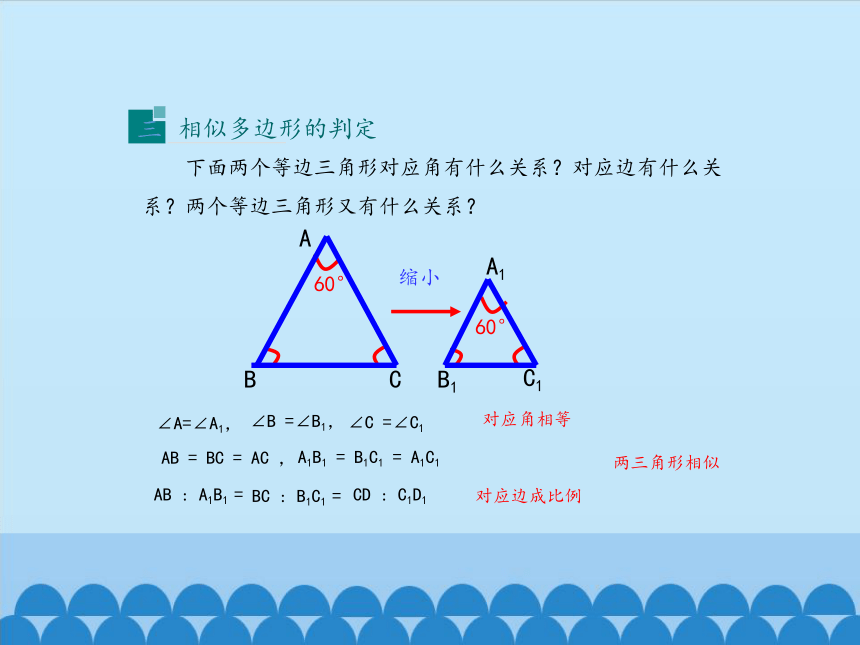
下面两个等边三角形对应角有什么关系?对应边有什么关系?两个等边三角形又有什么关系?
∠A=∠A1,
∠B
=∠B1,
∠C
=∠C1
AB
:
A1B1
=
BC
:
B1C1
=
CD
:
C1D1
AB
=
BC
=
AC
,
A1B1
=
B1C1
=
A1C1
60°
60°
对应角相等
对应边成比例
两三角形相似
放大
120°
120°
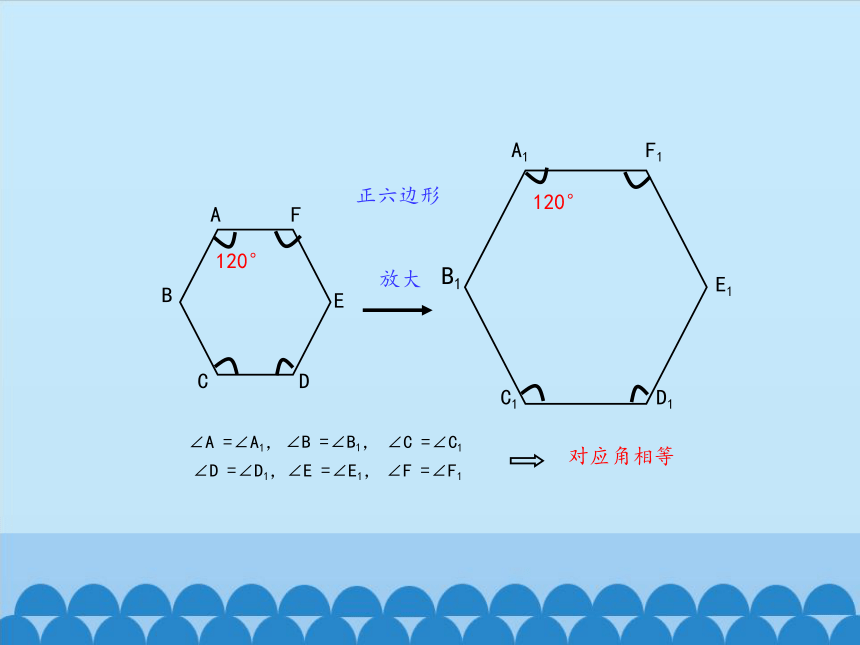
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1
对应角相等
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
∠D
=∠D1,
∠E
=∠E1,
∠F
=∠F1
正六边形
正六边形
放大
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
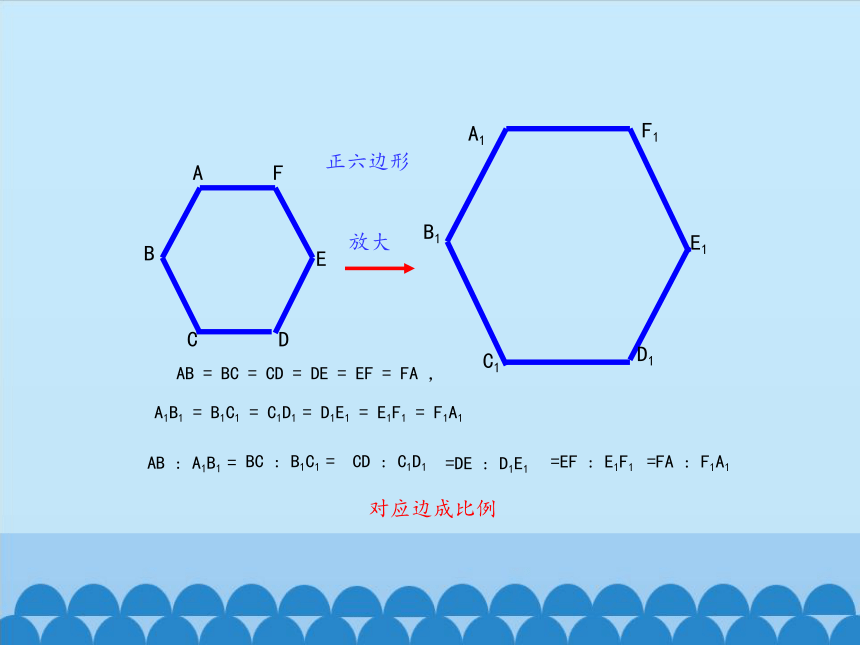
AB
=
BC
=
CD
=
DE
=
EF
=
FA
,
A1B1
=
B1C1
=
C1D1
=
D1E1
=
E1F1
=
F1A1
对应边成比例
AB
:
A1B1
=
BC
:
B1C1
=
CD
:
C1D1
=DE
:
D1E1
=EF
:
E1F1
=FA
:
F1A1
相似比:相似多边形对应边的比
相似多边形的定义:
两个边数相同的多边形,如果各边对应成比例,各角对应相等
,就称这两个多边形相似。
当堂练习
1.根据下图所示,这两个多边形相似吗?说说你的理由。
140
120
75
90
60
80
65
50
不相似,对应边不成比例。
如图所示的两个矩形是否相似?
不相似,大矩形的对应边成比例为20:12=5:3,
但小矩形的对应边成比例为(20-6):(12-6)=14:6=7:3。
当堂练习
课堂小结
3.相似比:相似多边形对应边的比
1.相似多边形的性质:
对应角相等
,对应边成比例(对应边的比相等)。
2.相似多边形的定义:
两个边数相同的多边形,如果各边对应成比例,各角对应相等,就称这两个多边形相似。
位似图形的概念及性质
一
在日常生活中,我们经常见到这样一类相似的图形,例如,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上(如图显示了它工作的原理)。在照相馆中,摄影师通过照相机,把人物的形象缩小在底片上。
这样的放大缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和满意的照片。
图中有多边形相似吗?如果有,那么这种相似有什么特征?
图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,这个点叫做位似中心。
O
O
概念形成:
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比。
探究归纳
位似图形的画法
二
2)
分别在线段OA、OB、OC、OD上取点A'
、B'
、C'
、D'
,使得
3)
顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'
就是所要求的图形。
O
D
A
B
C
A'
B'
C'
D'
利用位似,可以将一个图形放大或缩小。
1)
在四边形外任选一点O(如图),
1.把四边形ABCD
缩小到原来的
。
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A'、B'
、C'
、D'
,使得
呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形。
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
2.如图,△ABC,画△A
'
B
'
C
'
,使△A
'
B
'
C
'
∽△ABC,且使相似比为1.5。
要求:(1)位似中心在△ABC的一条边AB上;
(2)以点C为位似中心。
B
A
C
B
A
B
A
B
A
B
A
(1)位似中心在△ABC的一条边AB上
B
A
C
B
A
B
A
B
A
B
A
(2)以点C为位似中心
B
A
C
B
A
B
A
B
A
B
A
假设位似中心点O在AB上,
相似比1:5,点O位置如图
所示。
o
●
●
A
'
B
'
C
'
●
●
●
A
'
B
'
(C
'
)
●
●
2.利用位似进行作图的关键是确定位似中心和关键点。
3.位似分为内位似和外位似,内位似的位似中心在连接两个对应点的线段上;外位似的位似中心在连接两个对应点的线段之外。
1.画位似图形的一般步骤:
1)确定位似中心;
2)分别连接并延长位似中心和能代表原图的关键点;
3)根据相似比,确定能代表所作的位似图形的关键点;
4)顺次连接上述各点,得到放大或缩小的图形。
归纳
1.如图,△OAB
和△OCD是位似图形,AB与CD平行吗?为什么?
O
A
B
C
D
解:AB∥CD,理由如下:
∵△OAB与△ODC是位似图形,
∴△OAB
∽△OCD,
∴∠OAB=∠C,
AB∥CD。
当堂作业
2.
如图,以O为位似中心,将△ABC放大为原来的两倍。
O
解:①作射线OA、OB、OC
,
②分别在OA、OB
、OC
上取点A'
、B'
、C'
使得
③顺次连接A'
、B'
、C'
就是所要求图形。
A
B
C
A'
B'
C'
3.画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A
'
B
'
C
'
D
'
E
'
E
D
C
O
●
B
A
●
●
●
●
●
A
'
B
'
D
'
C
'
E
'
课堂小结
位似图形:如果两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行或者在一条直线上,像这样的两个图形叫做位似图形,这个点叫做位似中心。
2.位似图的性质:
(1)位似图形一定相似,位似比等于相似比;
(2)位似图形对应点和位似中心在同一条直线上;
(3)任意一对对应点到位似中心的距离之比等于位似比或相似比;
(4)对应线段平行或者在一条直线上。
谢谢
25.7相似多边形和图形的位似
1.理解相似图形的定义并能判断两图形是否相似。
2.学习并掌握相似多边形的性质与判定方法。(重点、难点)
3.理解并掌握位似图形的相关概念。
4.学习并掌握位似图形的性质并能够运用其解决问题。(重点)
学习目标
问题1
请观察下面几组图片,它们有何共同之处?
观察与思考
相同点:形状相同。
不同点:大小不相同。
相似图形的概念:
形状相同的图形叫做相似图形。
注意:相似图形的大小不一定相同。
归纳
相似多边形的性质
二
图中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系?
由此可以得到两个相似多边形的性质:
实际上这也是我们判定两个多边形是否相似的方法,即如果_______
_______
___
____,
那么这两个多边形相似。
对应边成比例,对应角相等
对应边成比例,对应角相等。
相似多边形的判定
三
A
B
C
A1
B1
C1
缩小
下面两个等边三角形对应角有什么关系?对应边有什么关系?两个等边三角形又有什么关系?
∠A=∠A1,
∠B
=∠B1,
∠C
=∠C1
AB
:
A1B1
=
BC
:
B1C1
=
CD
:
C1D1
AB
=
BC
=
AC
,
A1B1
=
B1C1
=
A1C1
60°
60°
对应角相等
对应边成比例
两三角形相似
放大
120°
120°
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1
对应角相等
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
∠D
=∠D1,
∠E
=∠E1,
∠F
=∠F1
正六边形
正六边形
放大
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
AB
=
BC
=
CD
=
DE
=
EF
=
FA
,
A1B1
=
B1C1
=
C1D1
=
D1E1
=
E1F1
=
F1A1
对应边成比例
AB
:
A1B1
=
BC
:
B1C1
=
CD
:
C1D1
=DE
:
D1E1
=EF
:
E1F1
=FA
:
F1A1
相似比:相似多边形对应边的比
相似多边形的定义:
两个边数相同的多边形,如果各边对应成比例,各角对应相等
,就称这两个多边形相似。
当堂练习
1.根据下图所示,这两个多边形相似吗?说说你的理由。
140
120
75
90
60
80
65
50
不相似,对应边不成比例。
如图所示的两个矩形是否相似?
不相似,大矩形的对应边成比例为20:12=5:3,
但小矩形的对应边成比例为(20-6):(12-6)=14:6=7:3。
当堂练习
课堂小结
3.相似比:相似多边形对应边的比
1.相似多边形的性质:
对应角相等
,对应边成比例(对应边的比相等)。
2.相似多边形的定义:
两个边数相同的多边形,如果各边对应成比例,各角对应相等,就称这两个多边形相似。
位似图形的概念及性质
一
在日常生活中,我们经常见到这样一类相似的图形,例如,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上(如图显示了它工作的原理)。在照相馆中,摄影师通过照相机,把人物的形象缩小在底片上。
这样的放大缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和满意的照片。
图中有多边形相似吗?如果有,那么这种相似有什么特征?
图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,这个点叫做位似中心。
O
O
概念形成:
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比。
探究归纳
位似图形的画法
二
2)
分别在线段OA、OB、OC、OD上取点A'
、B'
、C'
、D'
,使得
3)
顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'
就是所要求的图形。
O
D
A
B
C
A'
B'
C'
D'
利用位似,可以将一个图形放大或缩小。
1)
在四边形外任选一点O(如图),
1.把四边形ABCD
缩小到原来的
。
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A'、B'
、C'
、D'
,使得
呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形。
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
2.如图,△ABC,画△A
'
B
'
C
'
,使△A
'
B
'
C
'
∽△ABC,且使相似比为1.5。
要求:(1)位似中心在△ABC的一条边AB上;
(2)以点C为位似中心。
B
A
C
B
A
B
A
B
A
B
A
(1)位似中心在△ABC的一条边AB上
B
A
C
B
A
B
A
B
A
B
A
(2)以点C为位似中心
B
A
C
B
A
B
A
B
A
B
A
假设位似中心点O在AB上,
相似比1:5,点O位置如图
所示。
o
●
●
A
'
B
'
C
'
●
●
●
A
'
B
'
(C
'
)
●
●
2.利用位似进行作图的关键是确定位似中心和关键点。
3.位似分为内位似和外位似,内位似的位似中心在连接两个对应点的线段上;外位似的位似中心在连接两个对应点的线段之外。
1.画位似图形的一般步骤:
1)确定位似中心;
2)分别连接并延长位似中心和能代表原图的关键点;
3)根据相似比,确定能代表所作的位似图形的关键点;
4)顺次连接上述各点,得到放大或缩小的图形。
归纳
1.如图,△OAB
和△OCD是位似图形,AB与CD平行吗?为什么?
O
A
B
C
D
解:AB∥CD,理由如下:
∵△OAB与△ODC是位似图形,
∴△OAB
∽△OCD,
∴∠OAB=∠C,
AB∥CD。
当堂作业
2.
如图,以O为位似中心,将△ABC放大为原来的两倍。
O
解:①作射线OA、OB、OC
,
②分别在OA、OB
、OC
上取点A'
、B'
、C'
使得
③顺次连接A'
、B'
、C'
就是所要求图形。
A
B
C
A'
B'
C'
3.画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A
'
B
'
C
'
D
'
E
'
E
D
C
O
●
B
A
●
●
●
●
●
A
'
B
'
D
'
C
'
E
'
课堂小结
位似图形:如果两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行或者在一条直线上,像这样的两个图形叫做位似图形,这个点叫做位似中心。
2.位似图的性质:
(1)位似图形一定相似,位似比等于相似比;
(2)位似图形对应点和位似中心在同一条直线上;
(3)任意一对对应点到位似中心的距离之比等于位似比或相似比;
(4)对应线段平行或者在一条直线上。
谢谢
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
