福建省永春县第一重点高中2022届高三上学期数学周末训练卷(3)(2021.09.16) (PDF版含答案解析)
文档属性
| 名称 | 福建省永春县第一重点高中2022届高三上学期数学周末训练卷(3)(2021.09.16) (PDF版含答案解析) |

|
|
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 00:00:00 | ||
图片预览



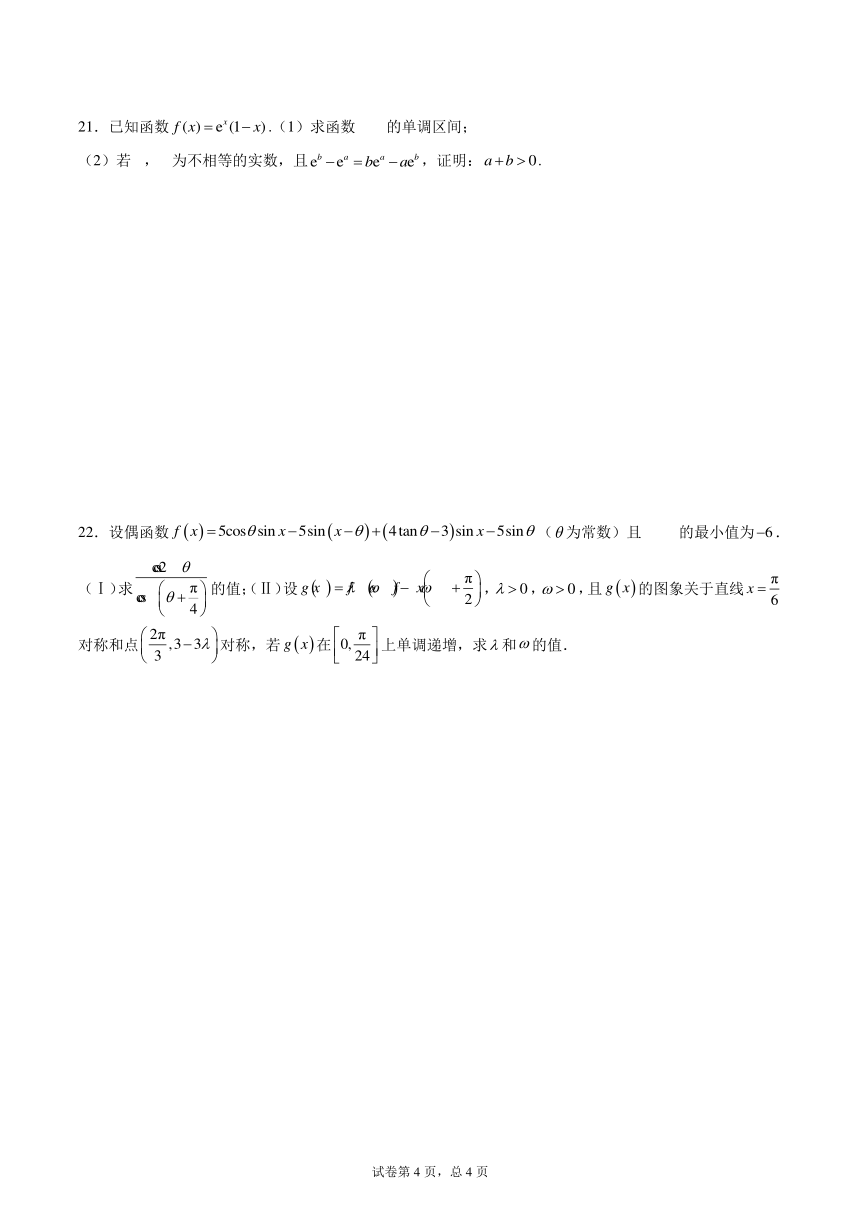

文档简介
高三年数学周末训练卷(3)2021
班级
体ABC
Q分别是棱AB
分别是直线AB,CD
点
迹围成的区域的面积是
最大值为
定义域为R的函数f(x)
)单调递减
得不等式
)<0成立的实数X的取值范
知函数f(x)
实数a的取值
1任意实数,且(a+2)
)2的最小值为
2
32
若直线y=kx+b是曲线
的切线,也是曲线
1的切线,则k+b
函数f(x)=xe-ax-a
零点,则实数a的取值范
8.数学中一般用
b
函数
有如
四个命题:①f(x)的最小正周期为丌
的图像关于直线X=一对称
(x)的值域
单调递增;其中是真命题的个数
9.如图所示,已知平面四边形ABCD,A
∠ADC
线AC将
翻折成
列说法正确
成角余弦
试卷第
点C到平面ABD的
最大值为≌20
知函数f(x)
R),则下列选项正确的是(
A.当
1
x)
的切线方程为y=2X
当a=-1时,函数f(x)在上单调递增
寸,函数
)时,f(x)≥2恒成立,则a≤1
(×)
在区间[-1+∞)上为增函数
定成立的是
设函数f(X)满足:①f(x)
函数f(x)与函数
1)交点的横坐标从左到右依次构成数列{an},则下列结论正确的是()
数f(x)的值域为01
对任意的k,b∈[01),数列{an}的前n项和Sn≠0
(×)是偶函数
2丌
知平
夹角为,且a-
的最小值是
4.如图,四棱锥P-ABCD的底面是边长为
方形,PA
若在四棱锥内挖
体积最大的
几何体的表面积等于
已知e,e2,e3是平面
是互相垂直的单位向量,若对任意A∈R均有
的最
16.已知函数f(
1时,若函数
有一个极值点,则实数的取值范围
若函数
的最大值为1,则
求
(2)设向量x=(
2B,1
X∥y,求in(B-A)的
知数f(xX)
的相邻两对称轴间的距离为
(1)求的解析
函数的图像向右平移。个单位长度
横坐标缩小为原来的-(纵坐
标不变),得到函数y=g(X)的图像,当
求函数
值域
(3)对于第(2
的函数g(X),记方程
依次为×,X
试确
的值,并求
知
1)当
求
(2)若f(×)的最小值为-1,求实数m的值
3)是否存在实数m,使函数9(
四个不同的零
知函数f(X)
求f(X)的单
知函数f(X)=e1-x).(1)求函数的单调区间
为不相等的实数
设偶函数f(x)=5cs0s
(x-0)+(
tan
8-3)sin
x
(为常数
最小值为
值:(Ⅱ)设g)=是和J-x
(×)的图象关于直线
对称和
对称,若
调递增,求4和ω的值
试卷第4
班级
体ABC
Q分别是棱AB
分别是直线AB,CD
点
迹围成的区域的面积是
最大值为
定义域为R的函数f(x)
)单调递减
得不等式
)<0成立的实数X的取值范
知函数f(x)
实数a的取值
1任意实数,且(a+2)
)2的最小值为
2
32
若直线y=kx+b是曲线
的切线,也是曲线
1的切线,则k+b
函数f(x)=xe-ax-a
零点,则实数a的取值范
8.数学中一般用
b
函数
有如
四个命题:①f(x)的最小正周期为丌
的图像关于直线X=一对称
(x)的值域
单调递增;其中是真命题的个数
9.如图所示,已知平面四边形ABCD,A
∠ADC
线AC将
翻折成
列说法正确
成角余弦
试卷第
点C到平面ABD的
最大值为≌20
知函数f(x)
R),则下列选项正确的是(
A.当
1
x)
的切线方程为y=2X
当a=-1时,函数f(x)在上单调递增
寸,函数
)时,f(x)≥2恒成立,则a≤1
(×)
在区间[-1+∞)上为增函数
定成立的是
设函数f(X)满足:①f(x)
函数f(x)与函数
1)交点的横坐标从左到右依次构成数列{an},则下列结论正确的是()
数f(x)的值域为01
对任意的k,b∈[01),数列{an}的前n项和Sn≠0
(×)是偶函数
2丌
知平
夹角为,且a-
的最小值是
4.如图,四棱锥P-ABCD的底面是边长为
方形,PA
若在四棱锥内挖
体积最大的
几何体的表面积等于
已知e,e2,e3是平面
是互相垂直的单位向量,若对任意A∈R均有
的最
16.已知函数f(
1时,若函数
有一个极值点,则实数的取值范围
若函数
的最大值为1,则
求
(2)设向量x=(
2B,1
X∥y,求in(B-A)的
知数f(xX)
的相邻两对称轴间的距离为
(1)求的解析
函数的图像向右平移。个单位长度
横坐标缩小为原来的-(纵坐
标不变),得到函数y=g(X)的图像,当
求函数
值域
(3)对于第(2
的函数g(X),记方程
依次为×,X
试确
的值,并求
知
1)当
求
(2)若f(×)的最小值为-1,求实数m的值
3)是否存在实数m,使函数9(
四个不同的零
知函数f(X)
求f(X)的单
知函数f(X)=e1-x).(1)求函数的单调区间
为不相等的实数
设偶函数f(x)=5cs0s
(x-0)+(
tan
8-3)sin
x
(为常数
最小值为
值:(Ⅱ)设g)=是和J-x
(×)的图象关于直线
对称和
对称,若
调递增,求4和ω的值
试卷第4
同课章节目录
