广东省广东实高2022届高三上学期9月阶段测试数学试题 (Word版含简答)
文档属性
| 名称 | 广东省广东实高2022届高三上学期9月阶段测试数学试题 (Word版含简答) |  | |
| 格式 | doc | ||
| 文件大小 | 852.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 19:14:59 | ||
图片预览




文档简介
广东实验中学2022届高三年级9月阶段性考试
数学
本试卷分选择题和非选择题两部分,共4页,满分150分,考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考号填写在答题卡上.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动用橡皮擦干净后,再选涂其它答案;不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在另发的答题卷各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁,考试结束后,将答题卷和答题卡一并收回.
第一部分选择题(共60分)
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有项是符合题目要求的)
1.
若集合中只有一个元素,则
A.
B.
C.
0
D.
0或
2.
某工厂生产的30个零件编号为01,02,…,19,30,现利用如下随机数表从中抽取5个进行检测.
若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件编号为(
)
34
57
07
86
36
04
68
96
08
23
23
45
78
89
07
84
42
12
53
31
25
30
07
32
86
32
21
18
34
29
78
64
54
07
32
52
42
06
44
38
12
23
43
56
77
35
78
90
56
42
A.
B.
C.
D.
3.
设复数满足(是虚数单位),则最大值为(
)
A.
B.
2
C.
D.
3
4.
已知等比数列中,,则的值为
A.
B.
C.
D.
5.
若函数的大致图像如图所示,则的解析式可以为(
)
A.
B.
C.
D.
6.
数列满足,对任意的m,都有,则
A.
B.
C.
D.
7.
已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A.
B.
C.
D.
8.
分形几何学是一门以不规则几何形态为研究对象的几何学.如图,有一列曲线P0,P1,…,Pn,….已知P0是边长为1的等边三角形,Pk+1是对Pk进行如下操作而得到:将Pk的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉..记Pn的周长为Ln、所围成的面积为Sn.对于,下列结论正确的是(
)
A.
为等差数列
B.
为等比数列
C.
,使
D.
,使
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.
已知等比数列的前项和为,公比,,则(
)
A.
一定是递增数列
B.
可能是递增数列也可能是递减数列
C
、、仍成等比
D.
,
10.
已知a,b是两条不同的直线,α,β,γ是三个不同的平面,下列命题中:
①若α∩β=a,β∩γ=b,且a//b,则α//γ;
②若a,
b相交,且都在α,β外,a//
α,
a//
β,b//α,
b//β,则α//β;
③若α⊥β,α∩β=a,b?β,
a⊥b,则b⊥α;
④若a?α,b?α,l⊥a,l⊥b,则l⊥α.其中正确命题的序号是(
)
A.
①②③
B.
①③
C.
②③
D.
①②③④
11.
已知无穷等差数列公差,且5,17,23是中的三项,则下列结论正确的是(
)
A.
d的最大值是6
B.
C.
一定是奇数
D.
137一定是数列中的项
12.
随着高三毕业日期的逐渐临近,有()个同学组成的学习小组,每人写了一个祝福的卡片准备送给其他同学,小组长收齐所有卡片后让每个人从中随机抽一张作为祝福卡片,则(
)
A.
当时,每个人抽到的卡片都不是自己的概率为
B.
当时,恰有一人抽到自己的卡片的概率为
C.
甲和乙恰好互换了卡片的概率为
D.
记个同学都拿到其他同学的卡片的抽法数为,则
第二部分非选择题(共9分)
二、填空题(本题共4小题,每小题5分,共20分)
13.
设是数列的前项和,且,,则__________.
14.
已知数列满足,且,,则数列的前2017项的和为_________.
15.
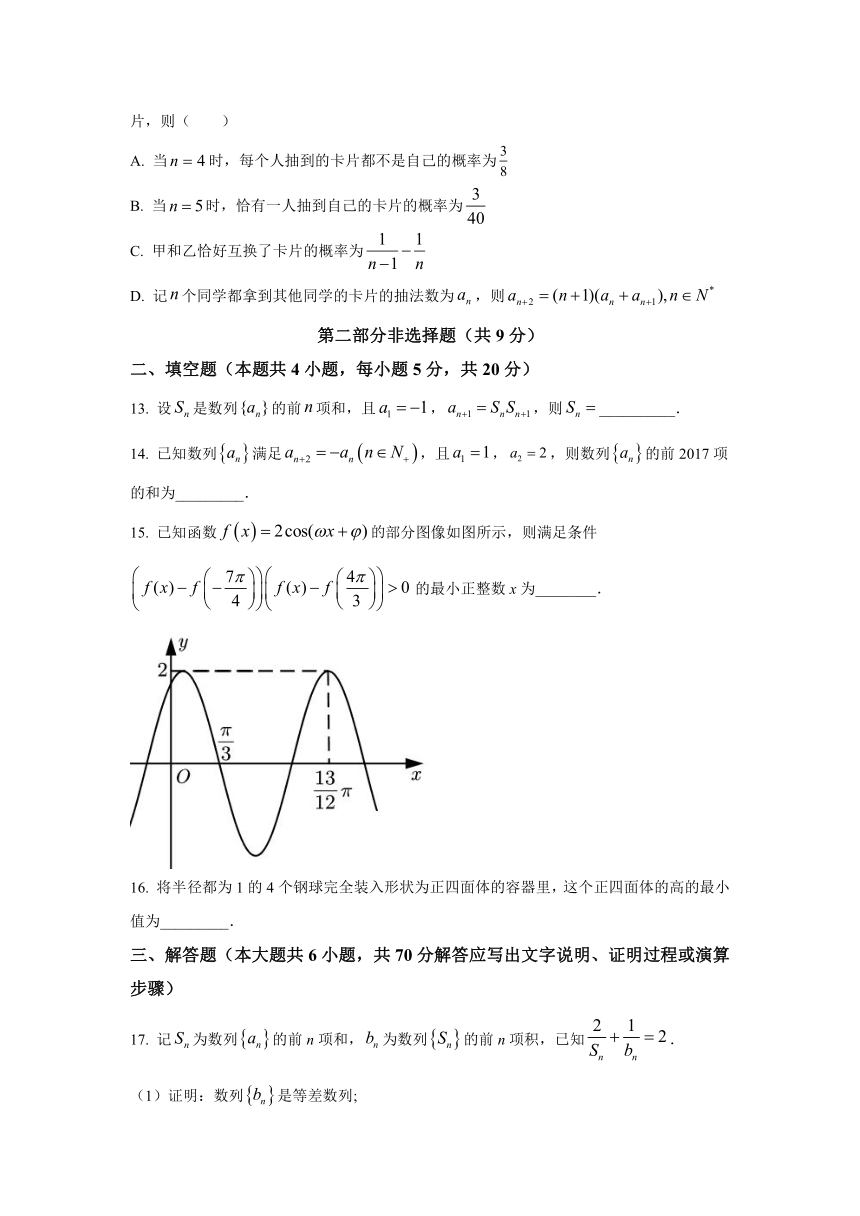
已知函数部分图像如图所示,则满足条件的最小正整数x为________.
16.
将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为_________.
三、解答题(本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤)
17.
记为数列的前n项和,为数列的前n项积,已知.
(1)证明:数列是等差数列;
(2)求的通项公式.
18.
已知数列,满足,对任意均有,.
(1)证明:数列和数列均为等比数列;
(2)设,求数列的前项和.
19.
已知数列,,,,,为数列的前n项和,为数列的前n项和.
(1)求数列的通项公式;
(2)求数列的前n项和;
(3)求证:.
20.
如图,四棱锥中,,,点F是AB的中点,点G在线段DC上,且.
(1)求证:平面CEF;
(2)若平面ABC,,,求锐二面角的余弦值.
21.
在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天)
人数
85
205
310
250
130
15
5
(1)求这1000名患者的潜伏期的样本平均值(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表请将列联表补充完整,并根据列联表判断是否有95%的把捏认为潜伏期与息者年龄有关;
潜伏期天
潜伏期天
总计
50岁以上(含50)
100
50岁以下
55
总计
200
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:,其中.
0.05
0.025
0.010
3841
5.024
6.635
22.
已知函数.
(1)求在点处的切线方程;
(2)若不等式恒成立,求k的取值范围;
(3)求证:当时,不等式成立.
广东实验中学2022届高三年级9月阶段性考试
数学
答案版
本试卷分选择题和非选择题两部分,共4页,满分150分,考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考号填写在答题卡上.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动用橡皮擦干净后,再选涂其它答案;不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在另发的答题卷各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁,考试结束后,将答题卷和答题卡一并收回.
第一部分选择题(共60分)
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有项是符合题目要求的)
1.
若集合中只有一个元素,则
A.
B.
C.
0
D.
0或
答案:D
2.
某工厂生产的30个零件编号为01,02,…,19,30,现利用如下随机数表从中抽取5个进行检测.
若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件编号为(
)
34
57
07
86
36
04
68
96
08
23
23
45
78
89
07
84
42
12
53
31
25
30
07
32
86
32
21
18
34
29
78
64
54
07
32
52
42
06
44
38
12
23
43
56
77
35
78
90
56
42
A.
B.
C.
D.
答案:C
3.
设复数满足(是虚数单位),则最大值为(
)
A.
B.
2
C.
D.
3
答案:C
4.
已知等比数列中,,则的值为
A.
B.
C.
D.
答案:D
5.
若函数的大致图像如图所示,则的解析式可以为(
)
A.
B.
C.
D.
答案:C
6.
数列满足,对任意的m,都有,则
A.
B.
C.
D.
答案:D
7.
已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A.
B.
C.
D.
答案:B
8.
分形几何学是一门以不规则几何形态为研究对象的几何学.如图,有一列曲线P0,P1,…,Pn,….已知P0是边长为1的等边三角形,Pk+1是对Pk进行如下操作而得到:将Pk的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉..记Pn的周长为Ln、所围成的面积为Sn.对于,下列结论正确的是(
)
A.
为等差数列
B.
为等比数列
C.
,使
D.
,使
答案:D
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.
已知等比数列的前项和为,公比,,则(
)
A.
一定是递增数列
B.
可能是递增数列也可能是递减数列
C
、、仍成等比
D.
,
答案:BCD
10.
已知a,b是两条不同的直线,α,β,γ是三个不同的平面,下列命题中:
①若α∩β=a,β∩γ=b,且a//b,则α//γ;
②若a,
b相交,且都在α,β外,a//
α,
a//
β,b//α,
b//β,则α//β;
③若α⊥β,α∩β=a,b?β,
a⊥b,则b⊥α;
④若a?α,b?α,l⊥a,l⊥b,则l⊥α.其中正确命题的序号是(
)
A.
①②③
B.
①③
C.
②③
D.
①②③④
答案:C
11.
已知无穷等差数列公差,且5,17,23是中的三项,则下列结论正确的是(
)
A.
d的最大值是6
B.
C.
一定是奇数
D.
137一定是数列中的项
答案:ABD
12.
随着高三毕业日期的逐渐临近,有()个同学组成的学习小组,每人写了一个祝福的卡片准备送给其他同学,小组长收齐所有卡片后让每个人从中随机抽一张作为祝福卡片,则(
)
A.
当时,每个人抽到的卡片都不是自己的概率为
B.
当时,恰有一人抽到自己的卡片的概率为
C.
甲和乙恰好互换了卡片的概率为
D.
记个同学都拿到其他同学的卡片的抽法数为,则
答案:ACD
第二部分非选择题(共9分)
二、填空题(本题共4小题,每小题5分,共20分)
13.
设是数列的前项和,且,,则__________.
答案:
14.
已知数列满足,且,,则数列的前2017项的和为_________.
答案:1
15.
已知函数部分图像如图所示,则满足条件的最小正整数x为________.
答案:2
16.
将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为_________.
答案:
三、解答题(本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤)
17.
记为数列的前n项和,为数列的前n项积,已知.
(1)证明:数列是等差数列;
(2)求的通项公式.
答案:(1)证明见解析;(2).
18.
已知数列,满足,对任意均有,.
(1)证明:数列和数列均为等比数列;
(2)设,求数列的前项和.
答案:(1)证明见解析;(2).
19.
已知数列,,,,,为数列的前n项和,为数列的前n项和.
(1)求数列的通项公式;
(2)求数列的前n项和;
(3)求证:.
答案:(1);(2);(3)证明见解析.
20.
如图,四棱锥中,,,点F是AB的中点,点G在线段DC上,且.
(1)求证:平面CEF;
(2)若平面ABC,,,求锐二面角的余弦值.
答案:(1)证明见解析;(2).
21.
在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天)
人数
85
205
310
250
130
15
5
(1)求这1000名患者的潜伏期的样本平均值(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表请将列联表补充完整,并根据列联表判断是否有95%的把捏认为潜伏期与息者年龄有关;
潜伏期天
潜伏期天
总计
50岁以上(含50)
100
50岁以下
55
总计
200
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:,其中.
0.05
0.025
0.010
3841
5.024
6.635
答案:(1)天;(2)列联表见解析,没有95%的把捏认为潜伏期与息者年龄有关.(3)潜伏期超过6天最有可能是8人.
22.
已知函数.
(1)求在点处的切线方程;
(2)若不等式恒成立,求k的取值范围;
(3)求证:当时,不等式成立.
答案:(1)(2)(3)证明见解析
数学
本试卷分选择题和非选择题两部分,共4页,满分150分,考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考号填写在答题卡上.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动用橡皮擦干净后,再选涂其它答案;不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在另发的答题卷各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁,考试结束后,将答题卷和答题卡一并收回.
第一部分选择题(共60分)
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有项是符合题目要求的)
1.
若集合中只有一个元素,则
A.
B.
C.
0
D.
0或
2.
某工厂生产的30个零件编号为01,02,…,19,30,现利用如下随机数表从中抽取5个进行检测.
若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件编号为(
)
34
57
07
86
36
04
68
96
08
23
23
45
78
89
07
84
42
12
53
31
25
30
07
32
86
32
21
18
34
29
78
64
54
07
32
52
42
06
44
38
12
23
43
56
77
35
78
90
56
42
A.
B.
C.
D.
3.
设复数满足(是虚数单位),则最大值为(
)
A.
B.
2
C.
D.
3
4.
已知等比数列中,,则的值为
A.
B.
C.
D.
5.
若函数的大致图像如图所示,则的解析式可以为(
)
A.
B.
C.
D.
6.
数列满足,对任意的m,都有,则
A.
B.
C.
D.
7.
已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A.
B.
C.
D.
8.
分形几何学是一门以不规则几何形态为研究对象的几何学.如图,有一列曲线P0,P1,…,Pn,….已知P0是边长为1的等边三角形,Pk+1是对Pk进行如下操作而得到:将Pk的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉..记Pn的周长为Ln、所围成的面积为Sn.对于,下列结论正确的是(
)
A.
为等差数列
B.
为等比数列
C.
,使
D.
,使
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.
已知等比数列的前项和为,公比,,则(
)
A.
一定是递增数列
B.
可能是递增数列也可能是递减数列
C
、、仍成等比
D.
,
10.
已知a,b是两条不同的直线,α,β,γ是三个不同的平面,下列命题中:
①若α∩β=a,β∩γ=b,且a//b,则α//γ;
②若a,
b相交,且都在α,β外,a//
α,
a//
β,b//α,
b//β,则α//β;
③若α⊥β,α∩β=a,b?β,
a⊥b,则b⊥α;
④若a?α,b?α,l⊥a,l⊥b,则l⊥α.其中正确命题的序号是(
)
A.
①②③
B.
①③
C.
②③
D.
①②③④
11.
已知无穷等差数列公差,且5,17,23是中的三项,则下列结论正确的是(
)
A.
d的最大值是6
B.
C.
一定是奇数
D.
137一定是数列中的项
12.
随着高三毕业日期的逐渐临近,有()个同学组成的学习小组,每人写了一个祝福的卡片准备送给其他同学,小组长收齐所有卡片后让每个人从中随机抽一张作为祝福卡片,则(
)
A.
当时,每个人抽到的卡片都不是自己的概率为
B.
当时,恰有一人抽到自己的卡片的概率为
C.
甲和乙恰好互换了卡片的概率为
D.
记个同学都拿到其他同学的卡片的抽法数为,则
第二部分非选择题(共9分)
二、填空题(本题共4小题,每小题5分,共20分)
13.
设是数列的前项和,且,,则__________.
14.
已知数列满足,且,,则数列的前2017项的和为_________.
15.
已知函数部分图像如图所示,则满足条件的最小正整数x为________.
16.
将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为_________.
三、解答题(本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤)
17.
记为数列的前n项和,为数列的前n项积,已知.
(1)证明:数列是等差数列;
(2)求的通项公式.
18.
已知数列,满足,对任意均有,.
(1)证明:数列和数列均为等比数列;
(2)设,求数列的前项和.
19.
已知数列,,,,,为数列的前n项和,为数列的前n项和.
(1)求数列的通项公式;
(2)求数列的前n项和;
(3)求证:.
20.
如图,四棱锥中,,,点F是AB的中点,点G在线段DC上,且.
(1)求证:平面CEF;
(2)若平面ABC,,,求锐二面角的余弦值.
21.
在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天)
人数
85
205
310
250
130
15
5
(1)求这1000名患者的潜伏期的样本平均值(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表请将列联表补充完整,并根据列联表判断是否有95%的把捏认为潜伏期与息者年龄有关;
潜伏期天
潜伏期天
总计
50岁以上(含50)
100
50岁以下
55
总计
200
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:,其中.
0.05
0.025
0.010
3841
5.024
6.635
22.
已知函数.
(1)求在点处的切线方程;
(2)若不等式恒成立,求k的取值范围;
(3)求证:当时,不等式成立.
广东实验中学2022届高三年级9月阶段性考试
数学
答案版
本试卷分选择题和非选择题两部分,共4页,满分150分,考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考号填写在答题卡上.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动用橡皮擦干净后,再选涂其它答案;不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在另发的答题卷各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁,考试结束后,将答题卷和答题卡一并收回.
第一部分选择题(共60分)
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有项是符合题目要求的)
1.
若集合中只有一个元素,则
A.
B.
C.
0
D.
0或
答案:D
2.
某工厂生产的30个零件编号为01,02,…,19,30,现利用如下随机数表从中抽取5个进行检测.
若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件编号为(
)
34
57
07
86
36
04
68
96
08
23
23
45
78
89
07
84
42
12
53
31
25
30
07
32
86
32
21
18
34
29
78
64
54
07
32
52
42
06
44
38
12
23
43
56
77
35
78
90
56
42
A.
B.
C.
D.
答案:C
3.
设复数满足(是虚数单位),则最大值为(
)
A.
B.
2
C.
D.
3
答案:C
4.
已知等比数列中,,则的值为
A.
B.
C.
D.
答案:D
5.
若函数的大致图像如图所示,则的解析式可以为(
)
A.
B.
C.
D.
答案:C
6.
数列满足,对任意的m,都有,则
A.
B.
C.
D.
答案:D
7.
已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A.
B.
C.
D.
答案:B
8.
分形几何学是一门以不规则几何形态为研究对象的几何学.如图,有一列曲线P0,P1,…,Pn,….已知P0是边长为1的等边三角形,Pk+1是对Pk进行如下操作而得到:将Pk的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉..记Pn的周长为Ln、所围成的面积为Sn.对于,下列结论正确的是(
)
A.
为等差数列
B.
为等比数列
C.
,使
D.
,使
答案:D
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.
已知等比数列的前项和为,公比,,则(
)
A.
一定是递增数列
B.
可能是递增数列也可能是递减数列
C
、、仍成等比
D.
,
答案:BCD
10.
已知a,b是两条不同的直线,α,β,γ是三个不同的平面,下列命题中:
①若α∩β=a,β∩γ=b,且a//b,则α//γ;
②若a,
b相交,且都在α,β外,a//
α,
a//
β,b//α,
b//β,则α//β;
③若α⊥β,α∩β=a,b?β,
a⊥b,则b⊥α;
④若a?α,b?α,l⊥a,l⊥b,则l⊥α.其中正确命题的序号是(
)
A.
①②③
B.
①③
C.
②③
D.
①②③④
答案:C
11.
已知无穷等差数列公差,且5,17,23是中的三项,则下列结论正确的是(
)
A.
d的最大值是6
B.
C.
一定是奇数
D.
137一定是数列中的项
答案:ABD
12.
随着高三毕业日期的逐渐临近,有()个同学组成的学习小组,每人写了一个祝福的卡片准备送给其他同学,小组长收齐所有卡片后让每个人从中随机抽一张作为祝福卡片,则(
)
A.
当时,每个人抽到的卡片都不是自己的概率为
B.
当时,恰有一人抽到自己的卡片的概率为
C.
甲和乙恰好互换了卡片的概率为
D.
记个同学都拿到其他同学的卡片的抽法数为,则
答案:ACD
第二部分非选择题(共9分)
二、填空题(本题共4小题,每小题5分,共20分)
13.
设是数列的前项和,且,,则__________.
答案:
14.
已知数列满足,且,,则数列的前2017项的和为_________.
答案:1
15.
已知函数部分图像如图所示,则满足条件的最小正整数x为________.
答案:2
16.
将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为_________.
答案:
三、解答题(本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤)
17.
记为数列的前n项和,为数列的前n项积,已知.
(1)证明:数列是等差数列;
(2)求的通项公式.
答案:(1)证明见解析;(2).
18.
已知数列,满足,对任意均有,.
(1)证明:数列和数列均为等比数列;
(2)设,求数列的前项和.
答案:(1)证明见解析;(2).
19.
已知数列,,,,,为数列的前n项和,为数列的前n项和.
(1)求数列的通项公式;
(2)求数列的前n项和;
(3)求证:.
答案:(1);(2);(3)证明见解析.
20.
如图,四棱锥中,,,点F是AB的中点,点G在线段DC上,且.
(1)求证:平面CEF;
(2)若平面ABC,,,求锐二面角的余弦值.
答案:(1)证明见解析;(2).
21.
在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天)
人数
85
205
310
250
130
15
5
(1)求这1000名患者的潜伏期的样本平均值(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表请将列联表补充完整,并根据列联表判断是否有95%的把捏认为潜伏期与息者年龄有关;
潜伏期天
潜伏期天
总计
50岁以上(含50)
100
50岁以下
55
总计
200
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:,其中.
0.05
0.025
0.010
3841
5.024
6.635
答案:(1)天;(2)列联表见解析,没有95%的把捏认为潜伏期与息者年龄有关.(3)潜伏期超过6天最有可能是8人.
22.
已知函数.
(1)求在点处的切线方程;
(2)若不等式恒成立,求k的取值范围;
(3)求证:当时,不等式成立.
答案:(1)(2)(3)证明见解析
同课章节目录
