2021-2022学年华东师大版数学八年级下册17.4.1反比例函数课件(14张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版数学八年级下册17.4.1反比例函数课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 414.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
反比例函数
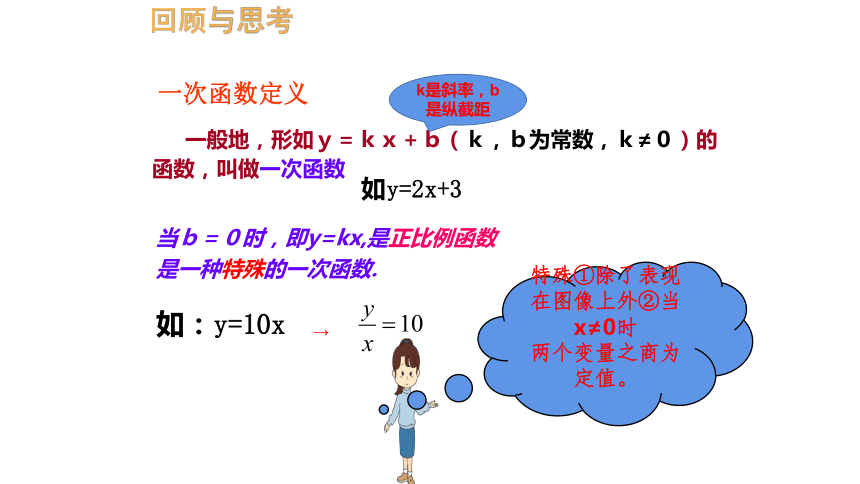
一次函数定义
一般地,形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数
当b=0时,即y=kx,是正比例函数
是一种特殊的一次函数.
回顾与思考
特殊①除了表现在图像上外②当x≠0时
两个变量之商为定值。
如y=2x+3
如:y=10x
k是斜率,b是纵截距
→
?
?
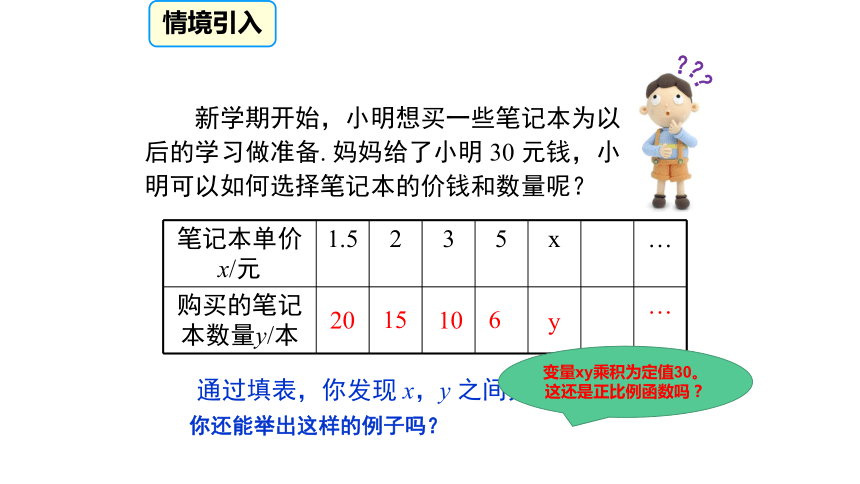
情境引入
新学期开始,小明想买一些笔记本为以后的学习做准备.
妈妈给了小明
30
元钱,小明可以如何选择笔记本的价钱和数量呢?
笔记本单价x/元
1.5
2
3
5
x
…
购买的笔记本数量y/本
…
通过填表,你发现
x,y
之间具有怎样的关系?
20
15
10
6
y
?
变量xy乘积为定值30。这还是正比例函数吗?
你还能举出这样的例子吗?
请你观察这两个式子的共同特点?
3、都能写成形如
(k是常数,k≠0)的式子。
2、等式右边是个分式,自变量位于分母位置,次数为1次;
1、自变量与函数值的积是一个定值。
称之为反比例
函数
形如
(k是常数,k≠0)的函数
叫做反比例函数。
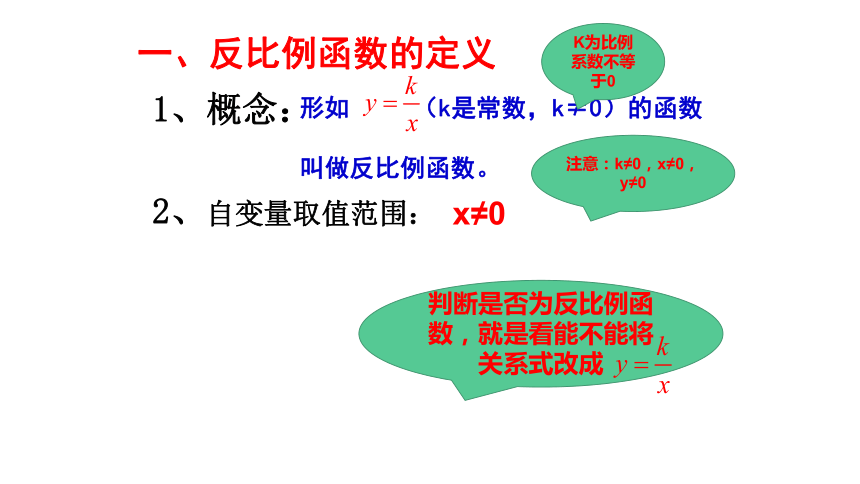
一、反比例函数的定义
1、概念:
2、自变量取值范围:
x≠0
判断是否为反比例函数,就是看能不能将关系式改成
注意:k≠0,x≠0,y≠0
K为比例系数不等于0
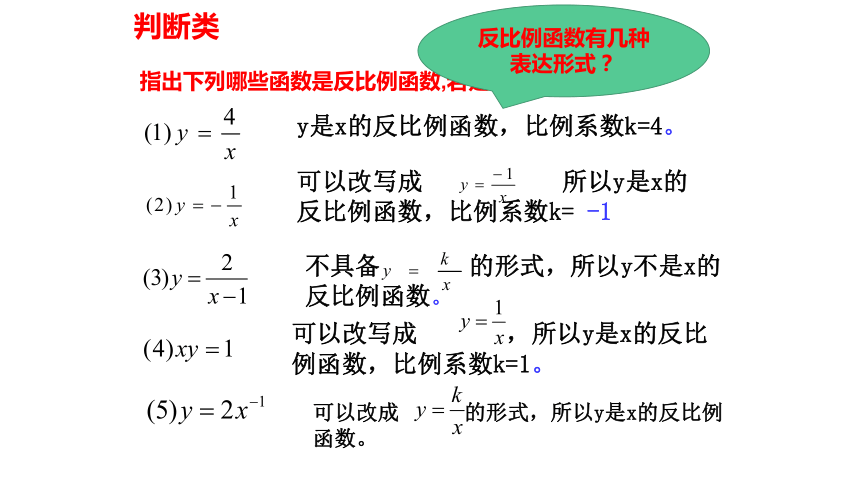
可以改写成
,所以y是x的反比例函数,比例系数k=1。
可以改成
的形式,所以y是x的反比例函数。
y是x的反比例函数,比例系数k=4。
不具备
的形式,所以y不是x的反比例函数。
可以改写成
所以y是x的
反比例函数,比例系数k=
-1
指出下列哪些函数是反比例函数,若是,请指出K值
判断类
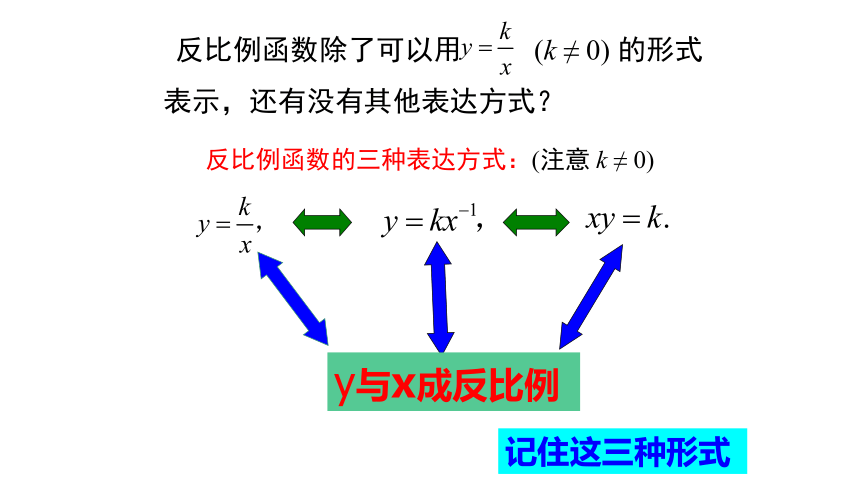
反比例函数有几种表达形式?
反比例函数除了可以用
(k
≠
0)
的形式表示,还有没有其他表达方式?
反比例函数的三种表达方式:(注意
k
≠
0)
y与x成反比例
记住这三种形式
例1:
例2:若函数
是反比例函数,求出m的值并写出解析式.
分析:
要求m的值
则需要建立关于m的方程,则需寻求一个等量关系式,而题中的信息只有反比例函数,它是那种形式来呈现了?
解:由
得m=±2,
又∵m-2≠0,
即
m≠2
∴
m=-2
∴解析式为
或
含参类
注意:不要漏掉K不为0.
若函数
是反比例
函数,求m的值。
a=-2
练习:
二
待定系数法求反比例函数的解析式
已知y是x的反比例函数,当x=2时,y=6
(1)求y与x的函数关系式;(2)求当x=4时,y的值。
例1:
解(1)设
由题意得:
解得:k=12
∴
(2)把x=4代入
得
y
=3
待定系数法的步骤:设--代--解--写
例2:已知y与x-1成反比例,当x
=
2时,y
=
4.
(1)用含有x的代数式表示y;
(2)当x=3时,求y的值.
解:(1)设y
=
(k≠0),
因为当
x=2时,y=4,所以4=
,
解得
k
=
4.
所以y
与
x
的函数表达式是
;
(2)当x
=
3时,y=
=2.
变式:
思考2:y是x的反比例函数,x是z的反比例函数,那么y是z的什么函数?
思考1若y与x
的成反比例关系则可设为(
)
若y+b与x的成反比例关系,则设为(
)
你有哪些收获?
一:课堂总结:
例1:若函数
是反比例函数,求k的值,并写出该反比例函数的解析式.
解:由题意得4-k2=0,且k-2≠0
,解得k=-2.
因此该反比例函数的解析式为
合力挑战
反比例函数
一次函数定义
一般地,形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数
当b=0时,即y=kx,是正比例函数
是一种特殊的一次函数.
回顾与思考
特殊①除了表现在图像上外②当x≠0时
两个变量之商为定值。
如y=2x+3
如:y=10x
k是斜率,b是纵截距
→
?
?
情境引入
新学期开始,小明想买一些笔记本为以后的学习做准备.
妈妈给了小明
30
元钱,小明可以如何选择笔记本的价钱和数量呢?
笔记本单价x/元
1.5
2
3
5
x
…
购买的笔记本数量y/本
…
通过填表,你发现
x,y
之间具有怎样的关系?
20
15
10
6
y
?
变量xy乘积为定值30。这还是正比例函数吗?
你还能举出这样的例子吗?
请你观察这两个式子的共同特点?
3、都能写成形如
(k是常数,k≠0)的式子。
2、等式右边是个分式,自变量位于分母位置,次数为1次;
1、自变量与函数值的积是一个定值。
称之为反比例
函数
形如
(k是常数,k≠0)的函数
叫做反比例函数。
一、反比例函数的定义
1、概念:
2、自变量取值范围:
x≠0
判断是否为反比例函数,就是看能不能将关系式改成
注意:k≠0,x≠0,y≠0
K为比例系数不等于0
可以改写成
,所以y是x的反比例函数,比例系数k=1。
可以改成
的形式,所以y是x的反比例函数。
y是x的反比例函数,比例系数k=4。
不具备
的形式,所以y不是x的反比例函数。
可以改写成
所以y是x的
反比例函数,比例系数k=
-1
指出下列哪些函数是反比例函数,若是,请指出K值
判断类
反比例函数有几种表达形式?
反比例函数除了可以用
(k
≠
0)
的形式表示,还有没有其他表达方式?
反比例函数的三种表达方式:(注意
k
≠
0)
y与x成反比例
记住这三种形式
例1:
例2:若函数
是反比例函数,求出m的值并写出解析式.
分析:
要求m的值
则需要建立关于m的方程,则需寻求一个等量关系式,而题中的信息只有反比例函数,它是那种形式来呈现了?
解:由
得m=±2,
又∵m-2≠0,
即
m≠2
∴
m=-2
∴解析式为
或
含参类
注意:不要漏掉K不为0.
若函数
是反比例
函数,求m的值。
a=-2
练习:
二
待定系数法求反比例函数的解析式
已知y是x的反比例函数,当x=2时,y=6
(1)求y与x的函数关系式;(2)求当x=4时,y的值。
例1:
解(1)设
由题意得:
解得:k=12
∴
(2)把x=4代入
得
y
=3
待定系数法的步骤:设--代--解--写
例2:已知y与x-1成反比例,当x
=
2时,y
=
4.
(1)用含有x的代数式表示y;
(2)当x=3时,求y的值.
解:(1)设y
=
(k≠0),
因为当
x=2时,y=4,所以4=
,
解得
k
=
4.
所以y
与
x
的函数表达式是
;
(2)当x
=
3时,y=
=2.
变式:
思考2:y是x的反比例函数,x是z的反比例函数,那么y是z的什么函数?
思考1若y与x
的成反比例关系则可设为(
)
若y+b与x的成反比例关系,则设为(
)
你有哪些收获?
一:课堂总结:
例1:若函数
是反比例函数,求k的值,并写出该反比例函数的解析式.
解:由题意得4-k2=0,且k-2≠0
,解得k=-2.
因此该反比例函数的解析式为
合力挑战
