第2章 对称性——圆单元测试(三) 2021—2022学年苏科版数学九年级上册(word版无答案)
文档属性
| 名称 | 第2章 对称性——圆单元测试(三) 2021—2022学年苏科版数学九年级上册(word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 379.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 09:51:13 | ||
图片预览

文档简介
2021年苏科版对称性——圆单元测试(三)(无答案)
一.选择题
1.若的半径为,点到圆心的距离为,那么点与的位置关系是(
)
A.点在圆外
B.点在圆上
C.点在圆内
D.不能确定
2.下列命题中,不正确的是(
)
A.垂直平分弦的直线经过圆心
B.平分弦的直径一定垂直于弦
C.平行弦所夹的两条弧相等
D.垂直于弦的直径必平分弦所对的弦
3.已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.不能确定
4.如图,在半圆中,是直径,是的中点,,则的度数为(
)
A.
B.
C.
D.
5.如图,在正十边形中,∠BAC的度数是( )
A.10°
B.18°
C.22.5°
D.36°
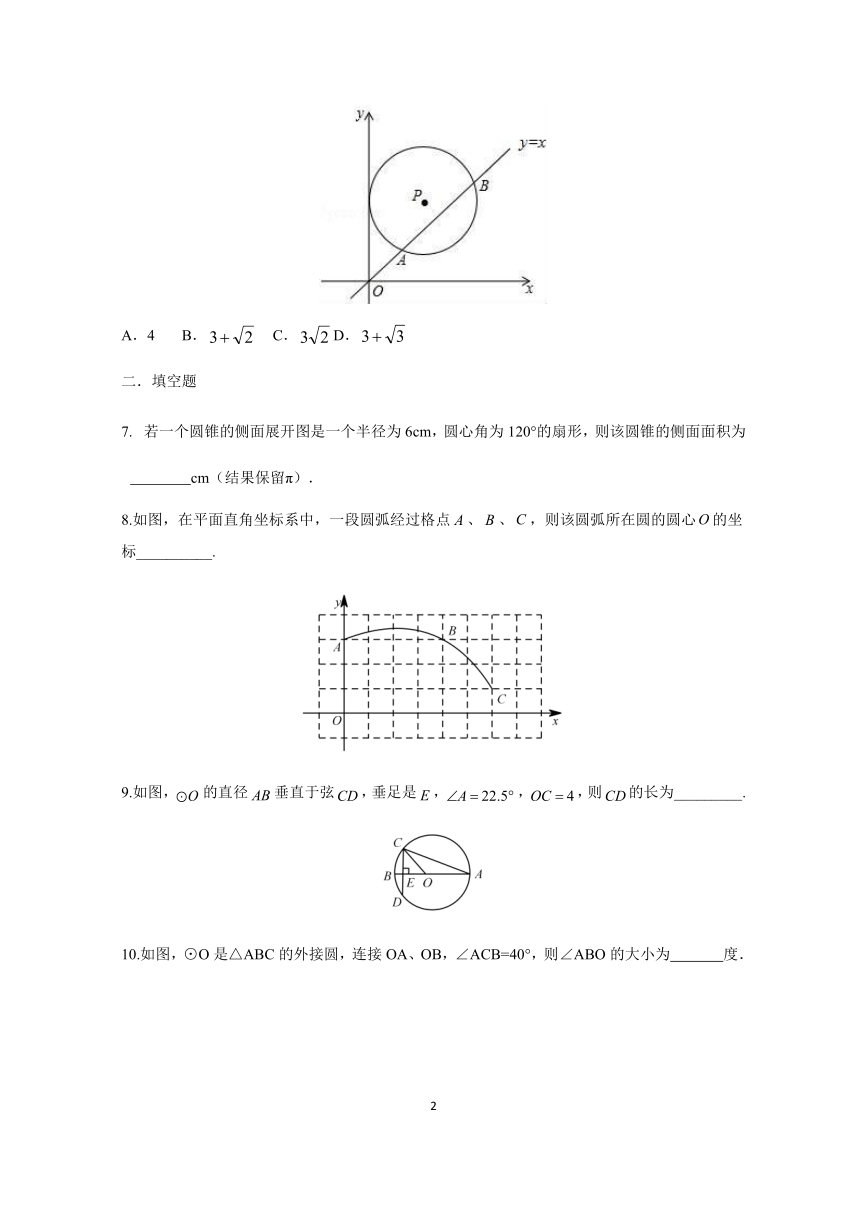
6.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4
B.
C.
D.
填空题
若一个圆锥的侧面展开图是一个半径为6cm,圆心角为120°的扇形,则该圆锥的侧面面积为
cm(结果保留π).
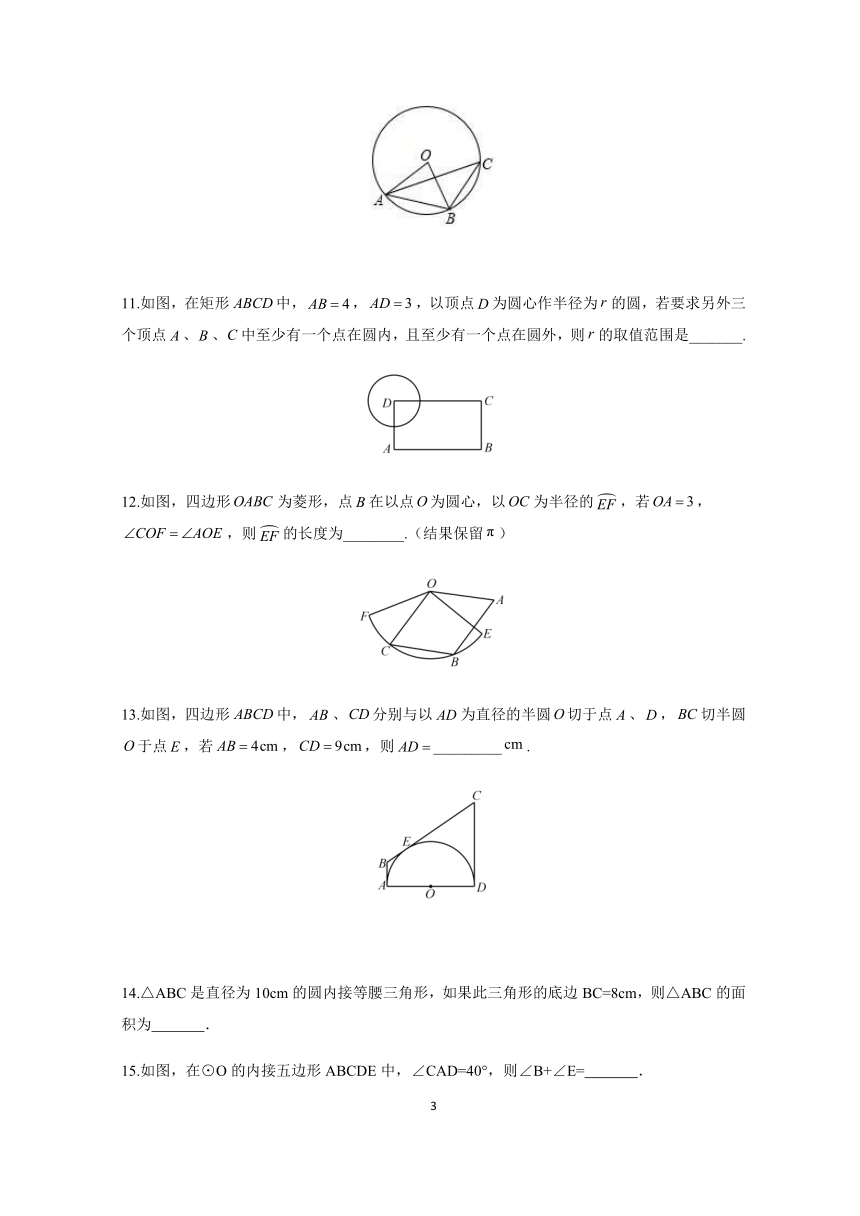
8.如图,在平面直角坐标系中,一段圆弧经过格点、、,则该圆弧所在圆的圆心的坐标__________.
9.如图,的直径垂直于弦,垂足是,,,则的长为_________.
10.如图,⊙O是△ABC的外接圆,连接OA、OB,∠ACB=40°,则∠ABO的大小为
度.
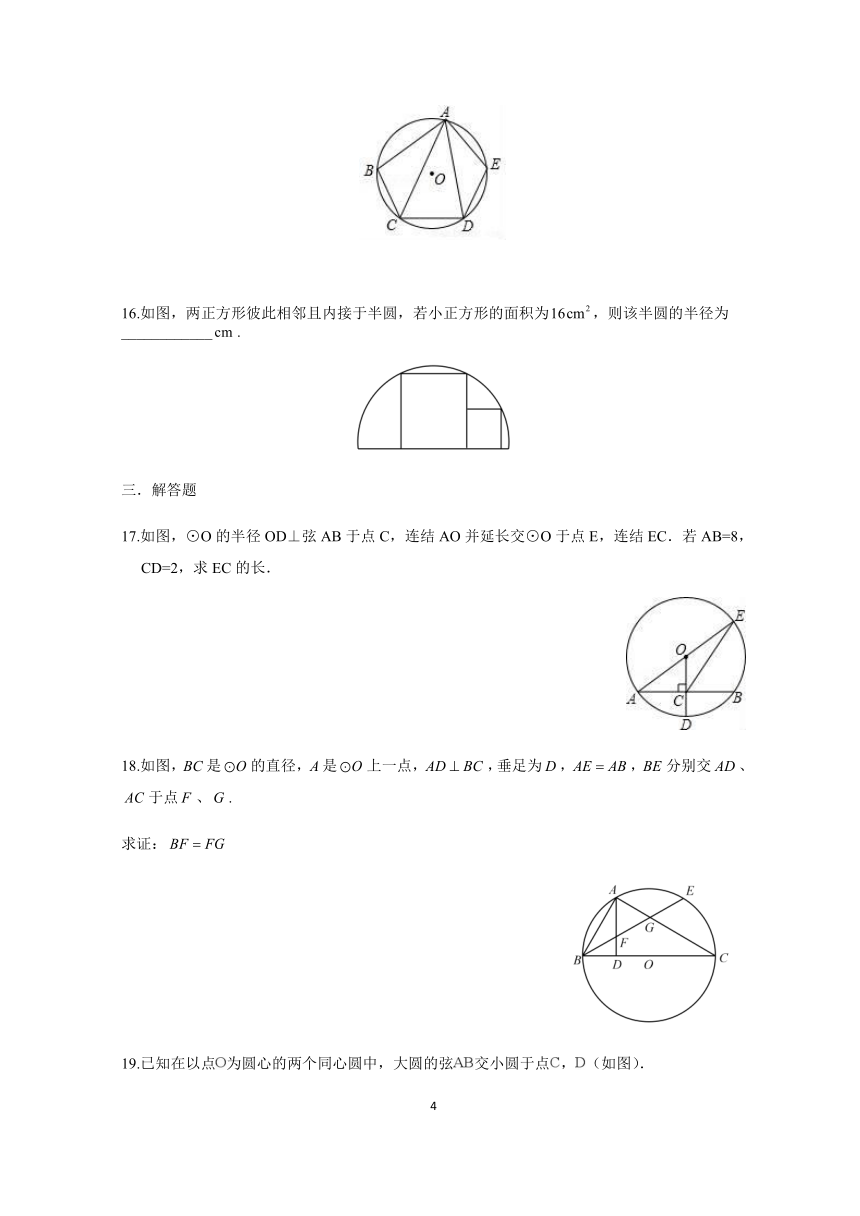
11.如图,在矩形中,,,以顶点为圆心作半径为的圆,若要求另外三个顶点、、中至少有一个点在圆内,且至少有一个点在圆外,则的取值范围是_______.
12.如图,四边形为菱形,点在以点为圆心,以为半径的,若,,则的长度为________.(结果保留)
13.如图,四边形中,、分别与以为直径的半圆切于点、,切半圆于点,若,,则_________.
14.△ABC是直径为10cm的圆内接等腰三角形,如果此三角形的底边BC=8cm,则△ABC的面积为
.
15.如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E=
.
16.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为,则该半圆的半径为____________.
三.解答题
17.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,求EC的长.
18.如图,是的直径,是上一点,,垂足为,,分别交、于点、.
求证:
19.已知在以点为圆心的两个同心圆中,大圆的弦交小圆于点,(如图).
()求证:.
()若大圆的半径,小圆的半径,且圆心到直线的距离为,求的长.
20.如图,是的外接圆,,是上一点.
(1)请你只用无刻度的直尺,分别画出图①和图②中的平分线;
(2)结合图②,说明你这样画的理由.
21.如图,在中,,点在上,以为直径的⊙与交于点,且平分.
()求证:是⊙的切线.
()若,,求⊙的半径.
22.如图,是的直径,、为上位于异侧的两点,连接并延长至点,使得,连接交于点,连接、、.
(1)证明:;
(2)若,求的度数;
(3)连接,若的直径为,,求的长.
23.如图,O为菱形ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M.
(1)求证:CD与⊙O相切;
(2)若菱形ABCD的边长为1,∠ABC=60°,求⊙O的半径.
24.如图①,是的一条弦,点是优弧上一点.
(1)若,点是上一点(不与、重合),则
(2)如图②,若点是弦与所围成的弓形区域(不含弦与)内一点.
求证:;
(3)请在图③中直接用阴影部分表示出在弦所围成的弓形区域内满足的点所在的范围.
25.是圆的内接三角形:
()如图,若,,,求圆的半径.
()如图,若,,,求的度数及圆的半径.
()如图,是圆的内接三角形,是边上的高,连结.
①请证明:.
②若,,,请求出圆的半径.
一.选择题
1.若的半径为,点到圆心的距离为,那么点与的位置关系是(
)
A.点在圆外
B.点在圆上
C.点在圆内
D.不能确定
2.下列命题中,不正确的是(
)
A.垂直平分弦的直线经过圆心
B.平分弦的直径一定垂直于弦
C.平行弦所夹的两条弧相等
D.垂直于弦的直径必平分弦所对的弦
3.已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.不能确定
4.如图,在半圆中,是直径,是的中点,,则的度数为(
)
A.
B.
C.
D.
5.如图,在正十边形中,∠BAC的度数是( )
A.10°
B.18°
C.22.5°
D.36°
6.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4
B.
C.
D.
填空题
若一个圆锥的侧面展开图是一个半径为6cm,圆心角为120°的扇形,则该圆锥的侧面面积为
cm(结果保留π).
8.如图,在平面直角坐标系中,一段圆弧经过格点、、,则该圆弧所在圆的圆心的坐标__________.
9.如图,的直径垂直于弦,垂足是,,,则的长为_________.
10.如图,⊙O是△ABC的外接圆,连接OA、OB,∠ACB=40°,则∠ABO的大小为
度.
11.如图,在矩形中,,,以顶点为圆心作半径为的圆,若要求另外三个顶点、、中至少有一个点在圆内,且至少有一个点在圆外,则的取值范围是_______.
12.如图,四边形为菱形,点在以点为圆心,以为半径的,若,,则的长度为________.(结果保留)
13.如图,四边形中,、分别与以为直径的半圆切于点、,切半圆于点,若,,则_________.
14.△ABC是直径为10cm的圆内接等腰三角形,如果此三角形的底边BC=8cm,则△ABC的面积为
.
15.如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E=
.
16.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为,则该半圆的半径为____________.
三.解答题
17.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,求EC的长.
18.如图,是的直径,是上一点,,垂足为,,分别交、于点、.
求证:
19.已知在以点为圆心的两个同心圆中,大圆的弦交小圆于点,(如图).
()求证:.
()若大圆的半径,小圆的半径,且圆心到直线的距离为,求的长.
20.如图,是的外接圆,,是上一点.
(1)请你只用无刻度的直尺,分别画出图①和图②中的平分线;
(2)结合图②,说明你这样画的理由.
21.如图,在中,,点在上,以为直径的⊙与交于点,且平分.
()求证:是⊙的切线.
()若,,求⊙的半径.
22.如图,是的直径,、为上位于异侧的两点,连接并延长至点,使得,连接交于点,连接、、.
(1)证明:;
(2)若,求的度数;
(3)连接,若的直径为,,求的长.
23.如图,O为菱形ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M.
(1)求证:CD与⊙O相切;
(2)若菱形ABCD的边长为1,∠ABC=60°,求⊙O的半径.
24.如图①,是的一条弦,点是优弧上一点.
(1)若,点是上一点(不与、重合),则
(2)如图②,若点是弦与所围成的弓形区域(不含弦与)内一点.
求证:;
(3)请在图③中直接用阴影部分表示出在弦所围成的弓形区域内满足的点所在的范围.
25.是圆的内接三角形:
()如图,若,,,求圆的半径.
()如图,若,,,求的度数及圆的半径.
()如图,是圆的内接三角形,是边上的高,连结.
①请证明:.
②若,,,请求出圆的半径.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
