2020-2021学年华东师大新版九年级上册《第23章 图形的相似》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版九年级上册《第23章 图形的相似》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 333.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 00:00:00 | ||
图片预览



文档简介
2020-2021学年华东师大新版九年级上册《第23章
图形的相似》单元测试卷
一.选择题
1.在平面直角坐标系中,下列各点属于第四象限的是( )
A.(1,2)
B.(﹣4,8)
C.(﹣3,﹣9)
D.(6,﹣7)
2.已知,那么下列式子中一定成立的是( )
A.x+y=5
B.2x=3y
C.
D.
3.已知=,那么下列等式中不一定正确的是( )
A.2x=5y
B.=
C.=
D.=
4.太原市轨道交通2号线一期于2020年12月26日12:00开通初期运营,从此山西驶入地铁时代.全线23个站厅的设计,有机融合了“晋阳古八景”、“锦绣太原城”等文化元素,打造成一条亮丽的“地下艺术走廊”在一幅比例尺为1:200000的设计图纸上,测得地铁线路全长约11.8cm,则地铁线路的实际长度约为( )
A.5.9km
B.11.8km.
C.23.6km
D.57.2km
5.如图,在△ABC中,DE∥AB,且,则的值为( )
A.
B.
C.
D.
6.如图,在△ABC中,DE∥BC,AD=4,DB=2,AE=3,则EC的长为( )
A.
B.1
C.2
D.
7.若2a=3b,则的值为( )
A.
B.
C.
D.
8.已知五边形ABCDE∽五边形FGHIJ,相似比为1:2,若五边形ABCDE的周长和面积分别为6和15,则五边形FGHIJ的周长和面积分别为( )
A.12和30
B.12和60
C.24和30
D.24和60
9.下列两个图形一定相似的是( )
A.任意两个矩形
B.任意两个等腰三角形
C.任意两个正方形
D.任意两个菱形
10.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(,称为黄金分割比例),著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例,且肚脐至足底的长度为108cm,则小凡的身高约为( )
A.155cm
B.165cm
C.175cm
D.185cm
二.填空题
11.已知点P(a,b)在第四象限,点P到x轴、y轴的距离分别为3、5,则a为
.
12.若,则的值为
.
13.已知,则的值是
.
14.已知=,则=
.
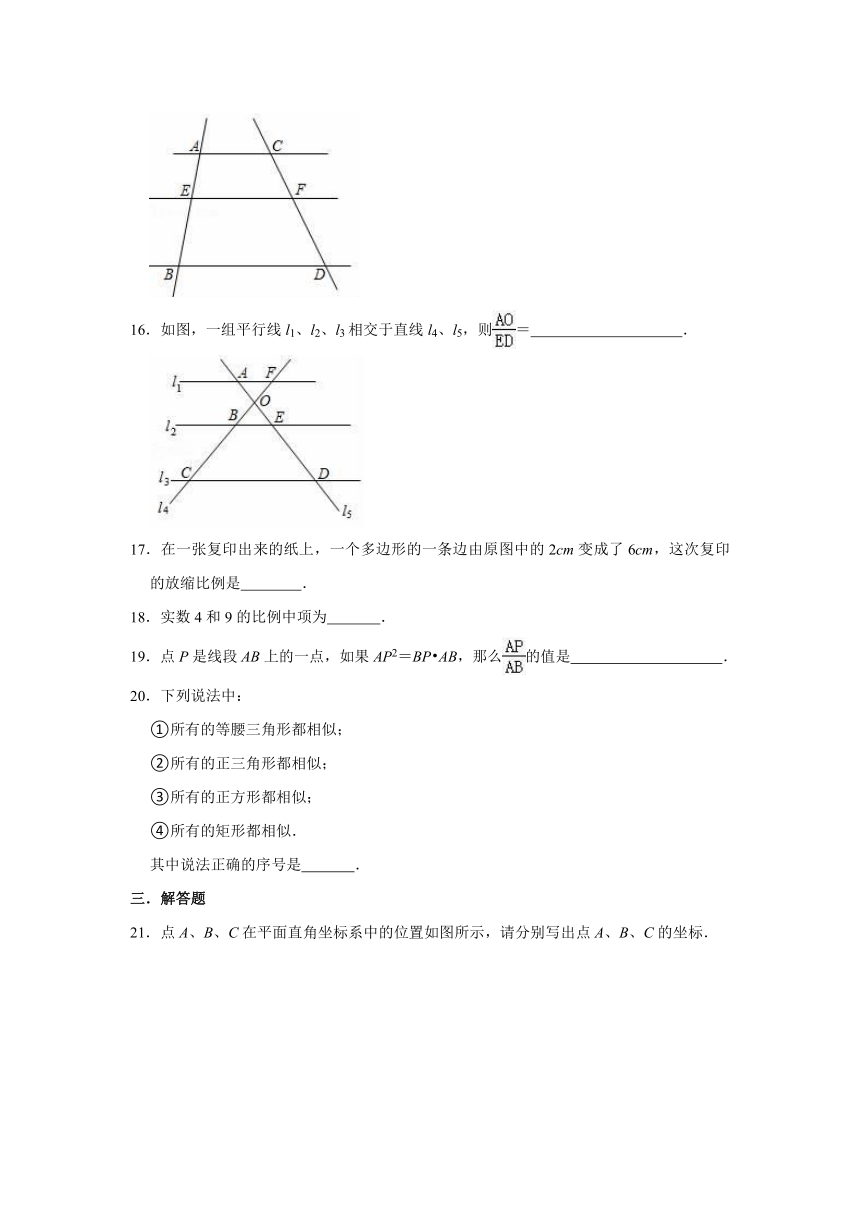
15.如图,已知AC∥EF∥BD,如果AE:EB=2:3,CD=6.那么CF的长等于
.
16.如图,一组平行线l1、l2、l3相交于直线l4、l5,则=
.
17.在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是
.
18.实数4和9的比例中项为
.
19.点P是线段AB上的一点,如果AP2=BP?AB,那么的值是
.
20.下列说法中:
①所有的等腰三角形都相似;
②所有的正三角形都相似;
③所有的正方形都相似;
④所有的矩形都相似.
其中说法正确的序号是
.
三.解答题
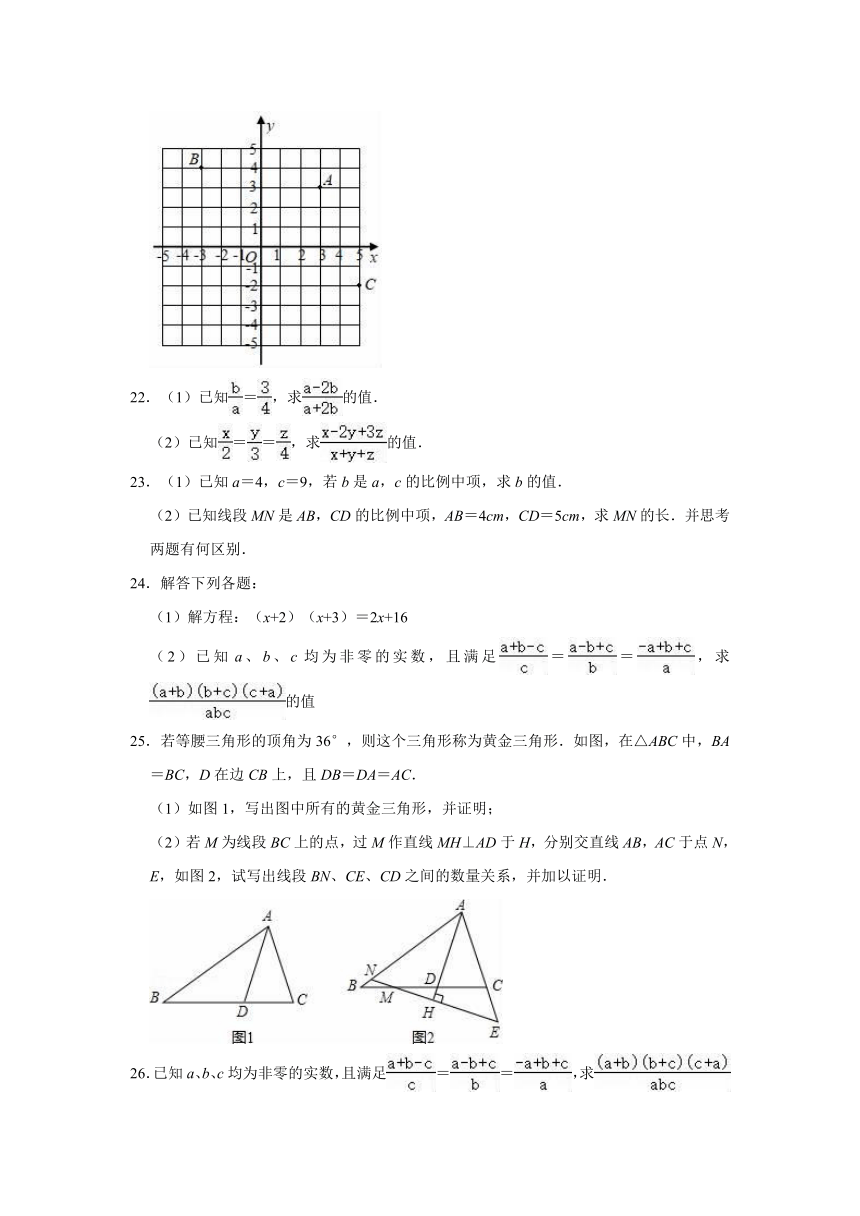
21.点A、B、C在平面直角坐标系中的位置如图所示,请分别写出点A、B、C的坐标.
22.(1)已知=,求的值.
(2)已知==,求的值.
23.(1)已知a=4,c=9,若b是a,c的比例中项,求b的值.
(2)已知线段MN是AB,CD的比例中项,AB=4cm,CD=5cm,求MN的长.并思考两题有何区别.
24.解答下列各题:
(1)解方程:(x+2)(x+3)=2x+16
(2)已知a、b、c均为非零的实数,且满足==,求的值
25.若等腰三角形的顶角为36°,则这个三角形称为黄金三角形.如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB,AC于点N,E,如图2,试写出线段BN、CE、CD之间的数量关系,并加以证明.
26.已知a、b、c均为非零的实数,且满足==,求的值.
参考答案与试题解析
一.选择题
1.解:A.(1,2)在第一象限,故本选项不合题意;
B.(﹣4,8)在第二象限,故本选项不合题意;
C.(﹣3,﹣9)在第三象限,故本选项不合题意;
D.(6,﹣7)在第四象限,故本选项符合题意;
故选:D.
2.解:∵,∴x+y=5不一定成立,A错误;
∵,∴3x=2y,∴2x=3y不成立,B错误;
∵,∴=,C错误,D正确,
故选:D.
3.解:∵=,
∴2x=5y,,,
∴A、B、C正确,D不一定正确;
故选:D.
4.解:设地铁线路的实际长度约为是x厘米,由题意,得
1:200000=11.8:x,
解得:x=2360000,
2360000厘米=23.6km.
故选:C.
5.解:∵=,
∴=,
∵DE∥AB,
∴==,
故选:A.
6.解:∵DE∥BC,AD=4,DB=2,AE=3,
∴=,即=,
解得,EC=,
故选:D.
7.解:∵2a=3b,
∴将等式两边都除以2b得=.
故选:D.
8.解:∵五边形ABCDE∽五边形FGHIJ,相似比为1:2,
∴五边形ABCDE和五边形FGHIJ的周长比是1:2,面积比是1:4,
∵五边形ABCDE的周长和面积分别为6和15,
∴五边形FGHIJ的周长和面积分别为12和60,
故选:B.
9.解:任意两个矩形,对应角对应相等、边的比不一定相等,不一定相似,A错误;
任意两个等腰三角形,形状不一定相同,不一定相似,B错误;
任意两个正方形对应角对应相等、边的比相等,所以相似,C正确;
任意两个菱形,边的比相等、对应角不一定相等,不一定相似,D错误,
故选:C.
10.解:设小凡的头顶至肚脐的长度为xcm,则小凡的身高为(x+108)cm,
由题意得:=,
∴x≈0.618×108=66.744(cm),
∴x+108≈175(cm),
即小凡的身高约为175cm,
故选:C.
二.填空题
11.解:∵点P在第四象限,且点P到x轴和y轴的距离分别为3,5,
∴点P的横坐标是5,纵坐标是﹣3,即点P的坐标为(5,﹣3),
∴a=5.
故答案为:5.
12.解:∵=,
∴==,
故答案为:.
13.解:∵
∴设a=2k,则b=3k.
∴==.
故答案为:.
14.解:∵=,
∴可设a=2k,b=3k(k≠0),
∴==.
故答案为.
15.解:∵AC∥EF∥BD,
∴=,即=,
解得,CF=,
故答案为:.
16.解:∵l1∥l2,
∴=①,
∵l2∥l3,
∴=②,
①×②,得=,
故答案为:.
17.解:由题意可知,相似多边形的边长之比=相似比=6:2=3:1,
故答案为:3:1;
18.解:根据比例中项的概念结合比例的基本性质得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是x,则
x2=4×9,
解得x=±6.
故答案为:±6.
19.解:∵点P是线段AB上的一点,AP2=BP?AB,
∴=,
∴点P是线段AB的黄金分割点,
∴AP=AB,
∴=,
故答案为:.
20.解:①所有的等腰三角形都相似,错误;
②所有的正三角形都相似,正确;
③所有的正方形都相似,正确;
④所有的矩形都相似,错误.
故答案为:②③.
三.解答题
21.解:由题意可知,点A的坐标为(3,3);点B的坐标为(﹣3,4);点C的坐标为(5,﹣2).
22.解:(1)∵=,
∴2b=1.5a,
∴==﹣;
(2)设===k(k≠0),则x=2k,y=3k,z=4k,
∴==.
23.解:(1)∵b是a,c的比例中项,
∴a:b=b:c,
∴b2=ac;
b=±,
∵a=4,c=9,
∴b=±=±6,即b=±6;
(2)∵MN是线段,
∴MN>0;
∵线段MN是AB,CD的比例中项,
∴AB:MN=MN:CD,
∴MN
2=AB?CD,
∴MN=±;
∵AB=4cm,CD=5cm,
∴MN=±=±2;
MN不可能为负值,则MN=2,
通过解答(1)、(2)发现,c、MN同时作为比例中项出现,c可以取负值,而MN不可以取负值.
24.解:(1)(x+2)(x+3)=2x+16,
x2+5x+6=2x+16,
x2+3x﹣10=0,
(x﹣2)(x+5)=0,
解得x1=2,x2=﹣5;
(2)若a+b+c≠0,由等比定理有====1,
所以a+b﹣c=c,a﹣b+c=b,﹣a+b+c=a,
于是有==8.
若a+b+c=0,则a+b=﹣c,b+c=﹣a,c+a=﹣b,
于是有==﹣1.
25.解:(1)△ABC和△ADC都是黄金三角形,理由如下:
∵BA=BC,
∴∠BAC=∠BCA,
∵DB=DA,
∴∠BAD=∠B,
∵DA═AC,
∴∠ADC=∠C=∠BAC=2∠B,
又∵∠B+∠BAC+∠C=180°,
∴∠B+2∠B+2∠B=180°,
∴∠B=∠DAC=36°,
∴△ABC和△ADC都是黄金三角形;
(2)CD=BN+CE,理由如下;
由(1)知,∠BAD=∠B=36°,∠CAD=36°=∠BAD,
∴AD是∠BAC的平分线,
在△ANH和△AEH中
∴△ANH≌△AEH(ASA),
∴AN=AE,
即AB﹣BN=AC+CE,
又∵BA=BC=BD+DC,AC=AD=BD,
∴BC﹣BN=AD+CE
∴BD+CD﹣BN=AD+CE,
又∵AD=BD,
∴CD﹣BN=CE,
即CD=BN+CE.
26.解:当a+b+c≠0时,
利用比例的性质化简已知等式得:=====1,
即a+b﹣c=c,a﹣b+c=b,﹣a+b+c=a,
整理得:a+b=2c,a+c=2b,b+c=2a,
此时原式==8;
当a+b+c=0时,可得:a+b=﹣c,a+c=﹣b,b+c=﹣a,
则原式=﹣1.
综上可知,的值为8或﹣1.
图形的相似》单元测试卷
一.选择题
1.在平面直角坐标系中,下列各点属于第四象限的是( )
A.(1,2)
B.(﹣4,8)
C.(﹣3,﹣9)
D.(6,﹣7)
2.已知,那么下列式子中一定成立的是( )
A.x+y=5
B.2x=3y
C.
D.
3.已知=,那么下列等式中不一定正确的是( )
A.2x=5y
B.=
C.=
D.=
4.太原市轨道交通2号线一期于2020年12月26日12:00开通初期运营,从此山西驶入地铁时代.全线23个站厅的设计,有机融合了“晋阳古八景”、“锦绣太原城”等文化元素,打造成一条亮丽的“地下艺术走廊”在一幅比例尺为1:200000的设计图纸上,测得地铁线路全长约11.8cm,则地铁线路的实际长度约为( )
A.5.9km
B.11.8km.
C.23.6km
D.57.2km
5.如图,在△ABC中,DE∥AB,且,则的值为( )
A.
B.
C.
D.
6.如图,在△ABC中,DE∥BC,AD=4,DB=2,AE=3,则EC的长为( )
A.
B.1
C.2
D.
7.若2a=3b,则的值为( )
A.
B.
C.
D.
8.已知五边形ABCDE∽五边形FGHIJ,相似比为1:2,若五边形ABCDE的周长和面积分别为6和15,则五边形FGHIJ的周长和面积分别为( )
A.12和30
B.12和60
C.24和30
D.24和60
9.下列两个图形一定相似的是( )
A.任意两个矩形
B.任意两个等腰三角形
C.任意两个正方形
D.任意两个菱形
10.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(,称为黄金分割比例),著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例,且肚脐至足底的长度为108cm,则小凡的身高约为( )
A.155cm
B.165cm
C.175cm
D.185cm
二.填空题
11.已知点P(a,b)在第四象限,点P到x轴、y轴的距离分别为3、5,则a为
.
12.若,则的值为
.
13.已知,则的值是
.
14.已知=,则=
.
15.如图,已知AC∥EF∥BD,如果AE:EB=2:3,CD=6.那么CF的长等于
.
16.如图,一组平行线l1、l2、l3相交于直线l4、l5,则=
.
17.在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是
.
18.实数4和9的比例中项为
.
19.点P是线段AB上的一点,如果AP2=BP?AB,那么的值是
.
20.下列说法中:
①所有的等腰三角形都相似;
②所有的正三角形都相似;
③所有的正方形都相似;
④所有的矩形都相似.
其中说法正确的序号是
.
三.解答题
21.点A、B、C在平面直角坐标系中的位置如图所示,请分别写出点A、B、C的坐标.
22.(1)已知=,求的值.
(2)已知==,求的值.
23.(1)已知a=4,c=9,若b是a,c的比例中项,求b的值.
(2)已知线段MN是AB,CD的比例中项,AB=4cm,CD=5cm,求MN的长.并思考两题有何区别.
24.解答下列各题:
(1)解方程:(x+2)(x+3)=2x+16
(2)已知a、b、c均为非零的实数,且满足==,求的值
25.若等腰三角形的顶角为36°,则这个三角形称为黄金三角形.如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB,AC于点N,E,如图2,试写出线段BN、CE、CD之间的数量关系,并加以证明.
26.已知a、b、c均为非零的实数,且满足==,求的值.
参考答案与试题解析
一.选择题
1.解:A.(1,2)在第一象限,故本选项不合题意;
B.(﹣4,8)在第二象限,故本选项不合题意;
C.(﹣3,﹣9)在第三象限,故本选项不合题意;
D.(6,﹣7)在第四象限,故本选项符合题意;
故选:D.
2.解:∵,∴x+y=5不一定成立,A错误;
∵,∴3x=2y,∴2x=3y不成立,B错误;
∵,∴=,C错误,D正确,
故选:D.
3.解:∵=,
∴2x=5y,,,
∴A、B、C正确,D不一定正确;
故选:D.
4.解:设地铁线路的实际长度约为是x厘米,由题意,得
1:200000=11.8:x,
解得:x=2360000,
2360000厘米=23.6km.
故选:C.
5.解:∵=,
∴=,
∵DE∥AB,
∴==,
故选:A.
6.解:∵DE∥BC,AD=4,DB=2,AE=3,
∴=,即=,
解得,EC=,
故选:D.
7.解:∵2a=3b,
∴将等式两边都除以2b得=.
故选:D.
8.解:∵五边形ABCDE∽五边形FGHIJ,相似比为1:2,
∴五边形ABCDE和五边形FGHIJ的周长比是1:2,面积比是1:4,
∵五边形ABCDE的周长和面积分别为6和15,
∴五边形FGHIJ的周长和面积分别为12和60,
故选:B.
9.解:任意两个矩形,对应角对应相等、边的比不一定相等,不一定相似,A错误;
任意两个等腰三角形,形状不一定相同,不一定相似,B错误;
任意两个正方形对应角对应相等、边的比相等,所以相似,C正确;
任意两个菱形,边的比相等、对应角不一定相等,不一定相似,D错误,
故选:C.
10.解:设小凡的头顶至肚脐的长度为xcm,则小凡的身高为(x+108)cm,
由题意得:=,
∴x≈0.618×108=66.744(cm),
∴x+108≈175(cm),
即小凡的身高约为175cm,
故选:C.
二.填空题
11.解:∵点P在第四象限,且点P到x轴和y轴的距离分别为3,5,
∴点P的横坐标是5,纵坐标是﹣3,即点P的坐标为(5,﹣3),
∴a=5.
故答案为:5.
12.解:∵=,
∴==,
故答案为:.
13.解:∵
∴设a=2k,则b=3k.
∴==.
故答案为:.
14.解:∵=,
∴可设a=2k,b=3k(k≠0),
∴==.
故答案为.
15.解:∵AC∥EF∥BD,
∴=,即=,
解得,CF=,
故答案为:.
16.解:∵l1∥l2,
∴=①,
∵l2∥l3,
∴=②,
①×②,得=,
故答案为:.
17.解:由题意可知,相似多边形的边长之比=相似比=6:2=3:1,
故答案为:3:1;
18.解:根据比例中项的概念结合比例的基本性质得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是x,则
x2=4×9,
解得x=±6.
故答案为:±6.
19.解:∵点P是线段AB上的一点,AP2=BP?AB,
∴=,
∴点P是线段AB的黄金分割点,
∴AP=AB,
∴=,
故答案为:.
20.解:①所有的等腰三角形都相似,错误;
②所有的正三角形都相似,正确;
③所有的正方形都相似,正确;
④所有的矩形都相似,错误.
故答案为:②③.
三.解答题
21.解:由题意可知,点A的坐标为(3,3);点B的坐标为(﹣3,4);点C的坐标为(5,﹣2).
22.解:(1)∵=,
∴2b=1.5a,
∴==﹣;
(2)设===k(k≠0),则x=2k,y=3k,z=4k,
∴==.
23.解:(1)∵b是a,c的比例中项,
∴a:b=b:c,
∴b2=ac;
b=±,
∵a=4,c=9,
∴b=±=±6,即b=±6;
(2)∵MN是线段,
∴MN>0;
∵线段MN是AB,CD的比例中项,
∴AB:MN=MN:CD,
∴MN
2=AB?CD,
∴MN=±;
∵AB=4cm,CD=5cm,
∴MN=±=±2;
MN不可能为负值,则MN=2,
通过解答(1)、(2)发现,c、MN同时作为比例中项出现,c可以取负值,而MN不可以取负值.
24.解:(1)(x+2)(x+3)=2x+16,
x2+5x+6=2x+16,
x2+3x﹣10=0,
(x﹣2)(x+5)=0,
解得x1=2,x2=﹣5;
(2)若a+b+c≠0,由等比定理有====1,
所以a+b﹣c=c,a﹣b+c=b,﹣a+b+c=a,
于是有==8.
若a+b+c=0,则a+b=﹣c,b+c=﹣a,c+a=﹣b,
于是有==﹣1.
25.解:(1)△ABC和△ADC都是黄金三角形,理由如下:
∵BA=BC,
∴∠BAC=∠BCA,
∵DB=DA,
∴∠BAD=∠B,
∵DA═AC,
∴∠ADC=∠C=∠BAC=2∠B,
又∵∠B+∠BAC+∠C=180°,
∴∠B+2∠B+2∠B=180°,
∴∠B=∠DAC=36°,
∴△ABC和△ADC都是黄金三角形;
(2)CD=BN+CE,理由如下;
由(1)知,∠BAD=∠B=36°,∠CAD=36°=∠BAD,
∴AD是∠BAC的平分线,
在△ANH和△AEH中
∴△ANH≌△AEH(ASA),
∴AN=AE,
即AB﹣BN=AC+CE,
又∵BA=BC=BD+DC,AC=AD=BD,
∴BC﹣BN=AD+CE
∴BD+CD﹣BN=AD+CE,
又∵AD=BD,
∴CD﹣BN=CE,
即CD=BN+CE.
26.解:当a+b+c≠0时,
利用比例的性质化简已知等式得:=====1,
即a+b﹣c=c,a﹣b+c=b,﹣a+b+c=a,
整理得:a+b=2c,a+c=2b,b+c=2a,
此时原式==8;
当a+b+c=0时,可得:a+b=﹣c,a+c=﹣b,b+c=﹣a,
则原式=﹣1.
综上可知,的值为8或﹣1.
