2021-2022学年九年级数学鲁教版(五四制)上册第1章反比例函数单元能力达标测评(word版 含答案)
文档属性
| 名称 | 2021-2022学年九年级数学鲁教版(五四制)上册第1章反比例函数单元能力达标测评(word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 371.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 20:23:04 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学上册《第1章反比例函数》单元能力达标测评(附答案)
一.选择题(共12小题,满分48分)
1.下列函数中,y是x的反比例函数的是( )
A.
B.
C.
D.
2.若函数y=(m2﹣3m+2)x|m|﹣3是反比例函数,则m的值是( )
A.1
B.﹣2
C.2或﹣2
D.2
3.若反比例函数的图象经过点(﹣1,2),则它的解析式是( )
A.
B.
C.
D.
4.如图,双曲线y=与直线y=mx相交于A、B两点,B点坐标为(﹣2,﹣3),则A点坐标为( )
A.(﹣2,﹣3)
B.(2,3)
C.(﹣2,3)
D.(2,﹣3)
5.函数y=﹣kx+k和函数y=在同一坐标系内的图象可能是( )
A.B.C.D.
6.若点A(﹣1,y1),B(2,y2),C(3,y3)都在反比例函数y=﹣的图象上,则下列关系式正确的是( )
A.y2<y3<y1
B.y3<y2<y1
C.y1<y3<y2
D.y1<y2<y3
7.若图中反比例函数的表达式均为,则阴影面积为4的有( )
A.1个
B.2个
C.3个
D.4个
8.已知反比例函数y=﹣,当y≤且y≠0时,自变量x的取值范围为( )
A.x<0
B.x≤﹣9
C.﹣9≤x<0
D.x≤﹣9或x>0
9.已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),下面四个判断正确的有( )
①反比例函数y2的解析式是y2=﹣
②两个函数图象还有另一交点,且坐标为(﹣2,﹣4)
③当x<﹣2或0<x<2时,y1<y2
④正比例函数y1与反比例函数y2都随x的增大而增大
A.1个
B.2个
C.3个
D.4个
10.一次函数y1=kx+b(k≠0)与反比例函数y2=(m≠0)在同一平面直角坐标系中的图象如图所示,若y1<y2,则x的取值范围是( )
A.﹣2<x<0或x>1
B.x<﹣2或0<x<1
C.x>1
D.x>﹣2
11.如图,A、B是反比例函数y=的图象上关于原点O对称的任意两点,过点A作AC⊥x轴于点C,连接BC,则△ABC的面积为( )
A.1
B.2
C.3
D.4
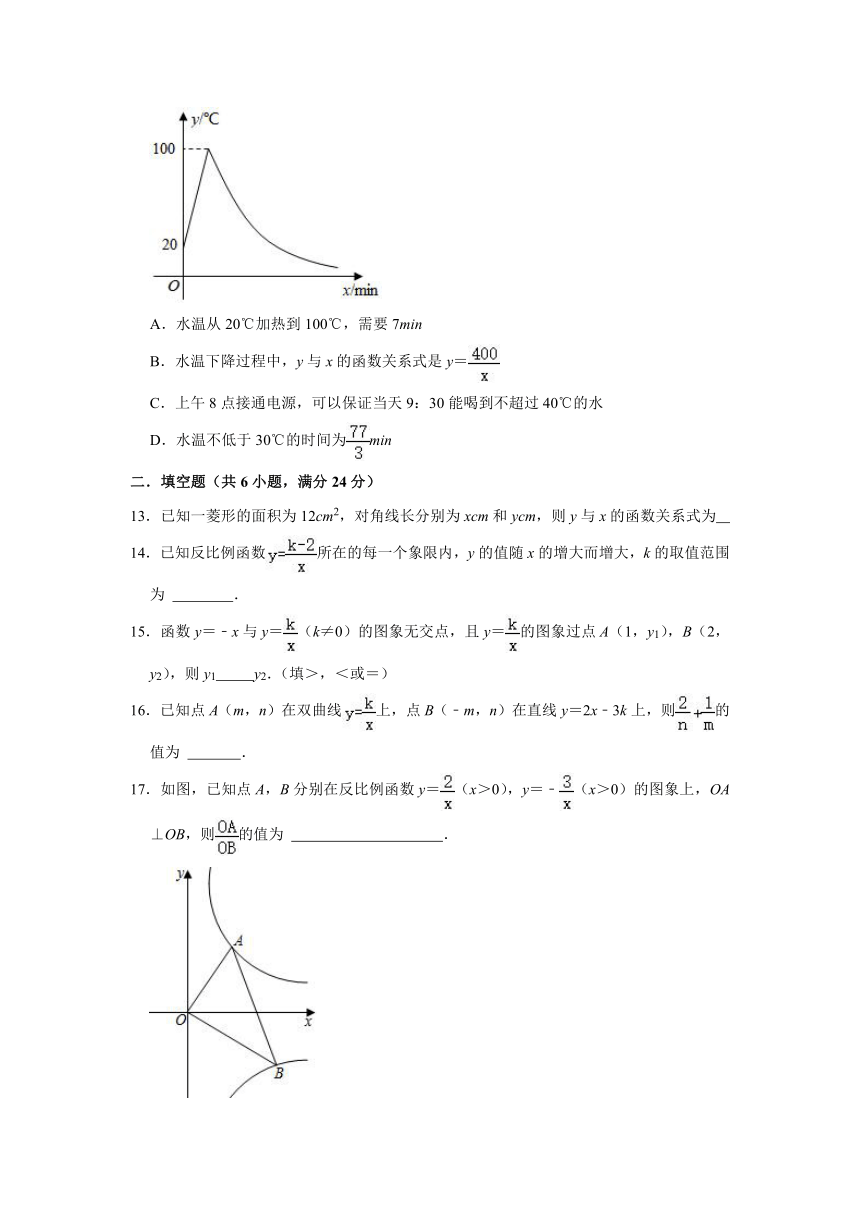
12.学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温y(℃)与通电时间x(min)成反比例关系.当水温将至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
A.水温从20℃加热到100℃,需要7min
B.水温下降过程中,y与x的函数关系式是y=
C.上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水
D.水温不低于30℃的时间为min
二.填空题(共6小题,满分24分)
13.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
14.已知反比例函数所在的每一个象限内,y的值随x的增大而增大,k的取值范围为
.
15.函数y=﹣x与y=(k≠0)的图象无交点,且y=的图象过点A(1,y1),B(2,y2),则y1
y2.(填>,<或=)
16.已知点A(m,n)在双曲线上,点B(﹣m,n)在直线y=2x﹣3k上,则的值为
.
17.如图,已知点A,B分别在反比例函数y=(x>0),y=﹣(x>0)的图象上,OA⊥OB,则的值为
.
18.如图,已知直线y=k1x+b(k1≠0)与x轴、y轴相交于Q、P两点,与y=(k2≠0)的图象相交于A(x1,y1),B(x2,y2)两点,连接OA、OB,现有以下4个结论:①k1k2>0;②不等式k1x+b>的解集是x1<x<x2;③x1+x2=﹣;④S△AOP=S△BOQ.其中正确结论的序号是
.(填上你认为正确的所有结论的序号)
三.解答题(共7小题,满分48分)
19.已知y=y1+2y2,y1与(x﹣2)成正比例,y2与x成反比例,且当x=1时,y=﹣1;当x=2时,y=3.
(1)求y关于x的函数解析式;
(2)当x=3时,求y的值.
20.如图,反比例函数y=的图象与正比例函数y=x的图象交于点A(m,﹣1)和B(4,n),点P(1,b)在反比例函数y=的图象上.
(1)求反比例函数的解析式和点P的坐标;
(2)连接AP,求△AOP的面积.
21.如图,已知直线y1=x+m与x轴、y轴分别交于点A,B,与双曲线y2=(x<0)分别交于点C,D,且点C的坐标为(﹣1,4).
(1)分别求直线、双曲线的函数表达式;
(2)求点D的坐标;
(3)利用函数图象直接写出:当x在什么范围内取值时y2<y1.
22.如图,A是反比例函数y=图象上一点,过点A作AB⊥y轴于点B,点C在x轴上,△ABC的面积为2.
(1)求反比例函数的解析式;
(2)已知OB=BA,点P(m,1)在该反比例函数的图象上,点Q是x轴上一动点,若QA+QP最小,求点Q的坐标.
23.如图,OA⊥OB,AB⊥x轴于C,点A(,1)在反比例函数y=的图象上.
(1)求反比例函数y=的表达式;
(2)在x轴的负半轴上存在一点P,使S△AOP=S△AOB,求点P的坐标.
24.已知一次函数y=kx+b的图象与反比例函数y=的图象在第一象限交于点A,与x轴交于点B,与y轴交于点C(0,﹣8),若CB=AB,且S△OAB=8.
(1)求反比例函数与一次函数的解析式;
(2)直接写出kx+b﹣<0的解集;
(3)若点P为y轴上一点,求使∠APB=90°的点P的坐标.
参考答案
一.选择题(共12小题,满分48分)
1.解:A.是反比例函数,故本选项符合题意;
B.不是反比例函数,故本选项不符合题意;
C.不是反比例函数,故本选项不符合题意;
D.不是反比例函数,故本选项不符合题意;
故选:A.
2.解:∵函数y=(m2﹣3m+2)x|m|﹣3是反比例函数,
∴|m|﹣3=﹣1,且m2﹣3m+2≠0,
∴m=±2,
当m=2时,m2﹣3m+2=0,不合题意舍去,
当m=﹣2时,m2﹣3m+2=12≠0,
∴m=﹣2,
故选:B.
3.解:设反比例函数解析式为y=,
∵反比例函数的图象经过点(﹣1,2),
∴k=﹣1×2=﹣2,
∴反比例函数解析式为y=﹣,
故选:B.
4.解:∵点A与B关于原点对称,
∴A点的坐标为(2,3).
故选:B.
5.解:①当k>0时,y=﹣kx+k过一、二、四象限;y=过一、三象限;
②当k<0时,y=﹣kx+k过一、三、四象象限;y=过二、四象限.
观察图形可知只有A符合.
故选:A.
6.解:将点A(﹣1,y1),B(2,y2),C(3,y3)分别代入y=﹣得,
y1=5,y2=﹣3,y3=﹣2,
故y2<y3<y1.
故选:A.
7.解:图1中,阴影面积为4;
图2中,阴影面积为×4=2;
图3中,阴影面积为2××4=4;
图4中,阴影面积为4××4=8;
则阴影面积为4的有2个.
故选:B.
8.解:如图所示:
∵反比例函数y=﹣,
k=﹣12,图像在二四象限,在每个象限内y随x的增大而增大,
当y=时,则x=﹣9,
故y≤且y≠0时,x≤﹣9或x>0.
故选:D.
9.解:由正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),可求出,
y1=2x,y2=,
因此①不正确;
由函数的对称性可得,两个函数图象还有另一交点,且坐标为(﹣2,﹣4)
因此②正确;
由两个函数的交点坐标以及函数的性质可得,当x<﹣2或0<x<2时,y1<y2,
因此③正确;
因为反比例函数,在每个象限内,y随x的增大而减小,
因此④不正确;
综上所述,正确的有②③,有两个,
故选:B.
10.解:由函数图象可知,当x<﹣2或0<x<1时,一次函数的图象在反比例函数图象的下方,
∴若y1<y2,则x的取值范围是x<﹣2或0<x<1.
故选:B.
11.解:由题意可知:△AOC的面积为1,
∵A、B关于原点O对称,
∴△AOC与△BOC的面积相等,
∴S△ABC=2S△AOC=2,
故选:B.
12.解:∵开机加热时每分钟上升10℃,
∴水温从20℃加热到100℃,所需时间为:=8min,
故A选项不合题意;
由题可得,(8,100)在反比例函数图象上,
设反比例函数解析式为y=,
代入点(8,100)可得,k=800,
∴水温下降过程中,y与x的函数关系式是y=,
故B选项不合题意;
令y=20,则=20,
∴x=40,
即饮水机每经过40分钟,要重新从20℃开始加热一次,
从8点9点30分钟,所用时间为90分钟,
而水温加热到100分钟,仅需要8分钟,
故当时间是9点30时,饮水机第三次加热,从20℃加热了10分钟,
令x=10,则y==80℃>40℃,
故C选项不符合题意;
水温从20℃加热到30℃所需要时间为:min,
令y=30,则=30,
∴,
∴水温不低于30℃的时间为=min,
故选:D.
二.填空题(共6小题,满分24分)
13.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
14.解:由题意得k﹣2<0,
∴k<2.
故答案为:k<2.
15.解:由于函数y=﹣x的图象经过二、四象限,而函数y=﹣x与y=(k≠0)的图象无交点,
所以k>0,
所以y=中,在每个象限内,y随x的增大而减小,
由1<2,
所以y1>y2,
故答案为:>.
16.解:∵点A(m,n)在双曲线上,
∴k=mn,
∴直线为y=2x﹣3mn,
∵点B(﹣m,n)在直线y=2x﹣3mn上,
∴n=﹣2m﹣3mn,
∴2m+n=﹣3mn,
∴===﹣3,
故答案为﹣3.
17.解:过点A作AM⊥y轴于点M,过点B作BN⊥y轴于点N,
∴∠AMO=∠BNO=90°,
∴∠AOM+∠OAM=90°,
∵OA⊥OB,
∴∠AOM+∠BON=90°,
∴∠OAM=∠BON,
∴△AOM∽△OBN,
∵点A,B分别在反比例函数y=(x>0),y=﹣(x>0)的图象上,
∴()2===,
∴=.
故答案为:.
18.解:①如图所示,直线y=kx1+b(k1≠0)经过第一、三象限,则k1>0.
双曲线y=(k2≠0)经过第一、三象限,则k2>0.
所以k1k2>0.
故结论①正确;
②如图所示:不等式kx1+b>的解集是x1<x<0或x>x2;
故结论②不正确;
③把A(x1,y1),B(x2,y2)的坐标代入y=k1x+b得,,
∴,
把A(x1,y1),B(x2,y2)的坐标代入,得x1y1=x2y2,
∴,
∴k1(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[k1(x1+x2)+b]=0,
∵x1≠x2,
∴k1(x1+x2)+b=0,
∴;
故结论③正确;
④把A(x1,y1),B(x2,y2)的坐标代入y=k1x+b得,,
解得,
∴直线解析式为,
∴点,,
把A(x1,y1),B(x2,y2)的坐标代入,得x1y1=x2y2,
∴,=
∴S△POB=S△QOA,
∴S△AOP=S△BOQ.
故结论④正确.
故答案是:①③④.
三.解答题(共7小题,满分48分)
19.解:(1)设y1=k1(x﹣2)(k1≠0),y2=(k2≠0),
∴y=k1(x﹣2)+.
∵当x=1时,y=﹣1.当x=2时,y=3,
∴,
∴,
∴y关于x的函数解析式是:y=7(x﹣2)+;
(2)由(1)知,y=7(x﹣2)+.则当x=3时,y=7+2=9.
20.解:(1)把点A(m,﹣1)和B(4,n)代入y=x得,﹣1=m,n=×4,
∴m=﹣4,n=1,
∴点A(﹣4,﹣1),B(4,1),
∵反比例函数y=的图象与正比例函数y=x的图象交于点A(﹣4,﹣1)和B,
∴k=﹣4×(﹣1)=4,
∴反比例函数的解析式为y=,
∵点P(1,b)在反比例函数的图象上.
∴b==4,
∴P(1,4);
(2)设直线AP的解析式为y=ax+d,
∵点A(﹣4,﹣1),P(1,4),
∴,解得,
∴直线AP为y=x+3,
设直线AP与y轴的交点为C,则C(0,3),
∴S△AOP=S△AOC+S△POC=+=.
21.解:(1)∵点C(﹣1,4)在直线y1=x+m上,
∴4=﹣1+m,
∴m=5,
∴直线的解析式为y1=x+5,
∵点C(﹣1,4)在双曲线,
∴4=,
∴k=﹣4,
∴双曲线的解析式为y2=;
(2)联立两函数解析式组成方程组,,
解得:或,
∴点D的坐标为(﹣4,1);
(3)观察函数图象,可知:当﹣4<x<﹣1时,y2<y1.
22.解:(1)连接OA,
∵△AOB的面积=△ABC的面积=3,△AOB的面积=|k|,
∴|k|=2,
∴k=±4;
又∵反比例函数的图象的一支位于第一象限,
∴k>0.
∴k=4.
∴这个反比例函数的解析式为y=;
(2)∵OB=BA,
∴设A(a,a),
∵反比例函数y=经过点A,
∴a2=4,
∴a=2,
∴A(2,2),
把y=1代入y=得,x=4,
∴P(4,1).
作点P关于x轴的对称点P′(4,﹣1),连接AP′与x轴交于点Q,此时QA+QP最小,
设过A,P′的直线表达式为y=mx+n,
∴,解得,
∴过A,P′的直线表达式为.
由,得.
∴点Q的坐标为.
23.解:(1)把A(,1)代入反比例函数y=得:k=1×=,
所以反比例函数的表达式为y=;
(2)∵A(,1),OA⊥AB,AB⊥x轴于C,
∴OC=,AC=1,
OA===2,
∵tanA==,
∴∠A=60°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠B=30°,
∴OB=2OC=2,
∴S△AOB===2,
∵S△AOP=S△AOB,
∴,
∵AC=1,
∴OP=2,
∴点P的坐标为(﹣2,0).
24.解:(1)如图1,过点A作AD⊥y轴于点D,则∠ADO=∠BOC=90°,
∴BO∥AD,
∴,
∵CB=AB,C(0,﹣8),
∴CO=DO=8,D(0,8),
∵S△OCB=S△OAB=8,
∴×CO×AD=S△OAC=16,
∴×8AD=16,
解得,AD=4,
∴A(4,8),
把A(4,8)代入y=,得8=,
解得,m=32,
把A(4,8)、C(0,﹣8)代入y=kx+b,
得,解得,
∴反比例函数与一次函数的解析式分别为y=和y=4x﹣8.
(2)如图2,设直线y=4x﹣8交双曲线y=的另一个交点是点E,
由得,或,
∴E(﹣2,﹣16),
由函数图象可知,当直线y=4x﹣8在双曲线y=的下方时,则x<﹣2
或0<x<4,
∴不等式kx+b<的解集是x<﹣2
或0<x<4,
由kx+b<得,kx+b﹣<0,
∴kx+b﹣<0的解集是x<﹣2
或0<x<4.
(3)如图3,设点P的坐标为(0,y),则PO=y,DP=8﹣y;
对于直线y=4x﹣8,当y=0时,由4x﹣8=0,得x=2,
∴B(2,0),
过点A作AD⊥y轴于点D,
则∠ADP=∠POB=∠APB=90°,
∴∠APD=90°﹣∠BPO=∠PBO,
∴△ADP∽△POB,
∴,
∴,
解得,y1=,y2=,
∴点P的坐标为(0,)或(0,).
一.选择题(共12小题,满分48分)
1.下列函数中,y是x的反比例函数的是( )
A.
B.
C.
D.
2.若函数y=(m2﹣3m+2)x|m|﹣3是反比例函数,则m的值是( )
A.1
B.﹣2
C.2或﹣2
D.2
3.若反比例函数的图象经过点(﹣1,2),则它的解析式是( )
A.
B.
C.
D.
4.如图,双曲线y=与直线y=mx相交于A、B两点,B点坐标为(﹣2,﹣3),则A点坐标为( )
A.(﹣2,﹣3)
B.(2,3)
C.(﹣2,3)
D.(2,﹣3)
5.函数y=﹣kx+k和函数y=在同一坐标系内的图象可能是( )
A.B.C.D.
6.若点A(﹣1,y1),B(2,y2),C(3,y3)都在反比例函数y=﹣的图象上,则下列关系式正确的是( )
A.y2<y3<y1
B.y3<y2<y1
C.y1<y3<y2
D.y1<y2<y3
7.若图中反比例函数的表达式均为,则阴影面积为4的有( )
A.1个
B.2个
C.3个
D.4个
8.已知反比例函数y=﹣,当y≤且y≠0时,自变量x的取值范围为( )
A.x<0
B.x≤﹣9
C.﹣9≤x<0
D.x≤﹣9或x>0
9.已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),下面四个判断正确的有( )
①反比例函数y2的解析式是y2=﹣
②两个函数图象还有另一交点,且坐标为(﹣2,﹣4)
③当x<﹣2或0<x<2时,y1<y2
④正比例函数y1与反比例函数y2都随x的增大而增大
A.1个
B.2个
C.3个
D.4个
10.一次函数y1=kx+b(k≠0)与反比例函数y2=(m≠0)在同一平面直角坐标系中的图象如图所示,若y1<y2,则x的取值范围是( )
A.﹣2<x<0或x>1
B.x<﹣2或0<x<1
C.x>1
D.x>﹣2
11.如图,A、B是反比例函数y=的图象上关于原点O对称的任意两点,过点A作AC⊥x轴于点C,连接BC,则△ABC的面积为( )
A.1
B.2
C.3
D.4
12.学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温y(℃)与通电时间x(min)成反比例关系.当水温将至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
A.水温从20℃加热到100℃,需要7min
B.水温下降过程中,y与x的函数关系式是y=
C.上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水
D.水温不低于30℃的时间为min
二.填空题(共6小题,满分24分)
13.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
14.已知反比例函数所在的每一个象限内,y的值随x的增大而增大,k的取值范围为
.
15.函数y=﹣x与y=(k≠0)的图象无交点,且y=的图象过点A(1,y1),B(2,y2),则y1
y2.(填>,<或=)
16.已知点A(m,n)在双曲线上,点B(﹣m,n)在直线y=2x﹣3k上,则的值为
.
17.如图,已知点A,B分别在反比例函数y=(x>0),y=﹣(x>0)的图象上,OA⊥OB,则的值为
.
18.如图,已知直线y=k1x+b(k1≠0)与x轴、y轴相交于Q、P两点,与y=(k2≠0)的图象相交于A(x1,y1),B(x2,y2)两点,连接OA、OB,现有以下4个结论:①k1k2>0;②不等式k1x+b>的解集是x1<x<x2;③x1+x2=﹣;④S△AOP=S△BOQ.其中正确结论的序号是
.(填上你认为正确的所有结论的序号)
三.解答题(共7小题,满分48分)
19.已知y=y1+2y2,y1与(x﹣2)成正比例,y2与x成反比例,且当x=1时,y=﹣1;当x=2时,y=3.
(1)求y关于x的函数解析式;
(2)当x=3时,求y的值.
20.如图,反比例函数y=的图象与正比例函数y=x的图象交于点A(m,﹣1)和B(4,n),点P(1,b)在反比例函数y=的图象上.
(1)求反比例函数的解析式和点P的坐标;
(2)连接AP,求△AOP的面积.
21.如图,已知直线y1=x+m与x轴、y轴分别交于点A,B,与双曲线y2=(x<0)分别交于点C,D,且点C的坐标为(﹣1,4).
(1)分别求直线、双曲线的函数表达式;
(2)求点D的坐标;
(3)利用函数图象直接写出:当x在什么范围内取值时y2<y1.
22.如图,A是反比例函数y=图象上一点,过点A作AB⊥y轴于点B,点C在x轴上,△ABC的面积为2.
(1)求反比例函数的解析式;
(2)已知OB=BA,点P(m,1)在该反比例函数的图象上,点Q是x轴上一动点,若QA+QP最小,求点Q的坐标.
23.如图,OA⊥OB,AB⊥x轴于C,点A(,1)在反比例函数y=的图象上.
(1)求反比例函数y=的表达式;
(2)在x轴的负半轴上存在一点P,使S△AOP=S△AOB,求点P的坐标.
24.已知一次函数y=kx+b的图象与反比例函数y=的图象在第一象限交于点A,与x轴交于点B,与y轴交于点C(0,﹣8),若CB=AB,且S△OAB=8.
(1)求反比例函数与一次函数的解析式;
(2)直接写出kx+b﹣<0的解集;
(3)若点P为y轴上一点,求使∠APB=90°的点P的坐标.
参考答案
一.选择题(共12小题,满分48分)
1.解:A.是反比例函数,故本选项符合题意;
B.不是反比例函数,故本选项不符合题意;
C.不是反比例函数,故本选项不符合题意;
D.不是反比例函数,故本选项不符合题意;
故选:A.
2.解:∵函数y=(m2﹣3m+2)x|m|﹣3是反比例函数,
∴|m|﹣3=﹣1,且m2﹣3m+2≠0,
∴m=±2,
当m=2时,m2﹣3m+2=0,不合题意舍去,
当m=﹣2时,m2﹣3m+2=12≠0,
∴m=﹣2,
故选:B.
3.解:设反比例函数解析式为y=,
∵反比例函数的图象经过点(﹣1,2),
∴k=﹣1×2=﹣2,
∴反比例函数解析式为y=﹣,
故选:B.
4.解:∵点A与B关于原点对称,
∴A点的坐标为(2,3).
故选:B.
5.解:①当k>0时,y=﹣kx+k过一、二、四象限;y=过一、三象限;
②当k<0时,y=﹣kx+k过一、三、四象象限;y=过二、四象限.
观察图形可知只有A符合.
故选:A.
6.解:将点A(﹣1,y1),B(2,y2),C(3,y3)分别代入y=﹣得,
y1=5,y2=﹣3,y3=﹣2,
故y2<y3<y1.
故选:A.
7.解:图1中,阴影面积为4;
图2中,阴影面积为×4=2;
图3中,阴影面积为2××4=4;
图4中,阴影面积为4××4=8;
则阴影面积为4的有2个.
故选:B.
8.解:如图所示:
∵反比例函数y=﹣,
k=﹣12,图像在二四象限,在每个象限内y随x的增大而增大,
当y=时,则x=﹣9,
故y≤且y≠0时,x≤﹣9或x>0.
故选:D.
9.解:由正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),可求出,
y1=2x,y2=,
因此①不正确;
由函数的对称性可得,两个函数图象还有另一交点,且坐标为(﹣2,﹣4)
因此②正确;
由两个函数的交点坐标以及函数的性质可得,当x<﹣2或0<x<2时,y1<y2,
因此③正确;
因为反比例函数,在每个象限内,y随x的增大而减小,
因此④不正确;
综上所述,正确的有②③,有两个,
故选:B.
10.解:由函数图象可知,当x<﹣2或0<x<1时,一次函数的图象在反比例函数图象的下方,
∴若y1<y2,则x的取值范围是x<﹣2或0<x<1.
故选:B.
11.解:由题意可知:△AOC的面积为1,
∵A、B关于原点O对称,
∴△AOC与△BOC的面积相等,
∴S△ABC=2S△AOC=2,
故选:B.
12.解:∵开机加热时每分钟上升10℃,
∴水温从20℃加热到100℃,所需时间为:=8min,
故A选项不合题意;
由题可得,(8,100)在反比例函数图象上,
设反比例函数解析式为y=,
代入点(8,100)可得,k=800,
∴水温下降过程中,y与x的函数关系式是y=,
故B选项不合题意;
令y=20,则=20,
∴x=40,
即饮水机每经过40分钟,要重新从20℃开始加热一次,
从8点9点30分钟,所用时间为90分钟,
而水温加热到100分钟,仅需要8分钟,
故当时间是9点30时,饮水机第三次加热,从20℃加热了10分钟,
令x=10,则y==80℃>40℃,
故C选项不符合题意;
水温从20℃加热到30℃所需要时间为:min,
令y=30,则=30,
∴,
∴水温不低于30℃的时间为=min,
故选:D.
二.填空题(共6小题,满分24分)
13.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
14.解:由题意得k﹣2<0,
∴k<2.
故答案为:k<2.
15.解:由于函数y=﹣x的图象经过二、四象限,而函数y=﹣x与y=(k≠0)的图象无交点,
所以k>0,
所以y=中,在每个象限内,y随x的增大而减小,
由1<2,
所以y1>y2,
故答案为:>.
16.解:∵点A(m,n)在双曲线上,
∴k=mn,
∴直线为y=2x﹣3mn,
∵点B(﹣m,n)在直线y=2x﹣3mn上,
∴n=﹣2m﹣3mn,
∴2m+n=﹣3mn,
∴===﹣3,
故答案为﹣3.
17.解:过点A作AM⊥y轴于点M,过点B作BN⊥y轴于点N,
∴∠AMO=∠BNO=90°,
∴∠AOM+∠OAM=90°,
∵OA⊥OB,
∴∠AOM+∠BON=90°,
∴∠OAM=∠BON,
∴△AOM∽△OBN,
∵点A,B分别在反比例函数y=(x>0),y=﹣(x>0)的图象上,
∴()2===,
∴=.
故答案为:.
18.解:①如图所示,直线y=kx1+b(k1≠0)经过第一、三象限,则k1>0.
双曲线y=(k2≠0)经过第一、三象限,则k2>0.
所以k1k2>0.
故结论①正确;
②如图所示:不等式kx1+b>的解集是x1<x<0或x>x2;
故结论②不正确;
③把A(x1,y1),B(x2,y2)的坐标代入y=k1x+b得,,
∴,
把A(x1,y1),B(x2,y2)的坐标代入,得x1y1=x2y2,
∴,
∴k1(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[k1(x1+x2)+b]=0,
∵x1≠x2,
∴k1(x1+x2)+b=0,
∴;
故结论③正确;
④把A(x1,y1),B(x2,y2)的坐标代入y=k1x+b得,,
解得,
∴直线解析式为,
∴点,,
把A(x1,y1),B(x2,y2)的坐标代入,得x1y1=x2y2,
∴,=
∴S△POB=S△QOA,
∴S△AOP=S△BOQ.
故结论④正确.
故答案是:①③④.
三.解答题(共7小题,满分48分)
19.解:(1)设y1=k1(x﹣2)(k1≠0),y2=(k2≠0),
∴y=k1(x﹣2)+.
∵当x=1时,y=﹣1.当x=2时,y=3,
∴,
∴,
∴y关于x的函数解析式是:y=7(x﹣2)+;
(2)由(1)知,y=7(x﹣2)+.则当x=3时,y=7+2=9.
20.解:(1)把点A(m,﹣1)和B(4,n)代入y=x得,﹣1=m,n=×4,
∴m=﹣4,n=1,
∴点A(﹣4,﹣1),B(4,1),
∵反比例函数y=的图象与正比例函数y=x的图象交于点A(﹣4,﹣1)和B,
∴k=﹣4×(﹣1)=4,
∴反比例函数的解析式为y=,
∵点P(1,b)在反比例函数的图象上.
∴b==4,
∴P(1,4);
(2)设直线AP的解析式为y=ax+d,
∵点A(﹣4,﹣1),P(1,4),
∴,解得,
∴直线AP为y=x+3,
设直线AP与y轴的交点为C,则C(0,3),
∴S△AOP=S△AOC+S△POC=+=.
21.解:(1)∵点C(﹣1,4)在直线y1=x+m上,
∴4=﹣1+m,
∴m=5,
∴直线的解析式为y1=x+5,
∵点C(﹣1,4)在双曲线,
∴4=,
∴k=﹣4,
∴双曲线的解析式为y2=;
(2)联立两函数解析式组成方程组,,
解得:或,
∴点D的坐标为(﹣4,1);
(3)观察函数图象,可知:当﹣4<x<﹣1时,y2<y1.
22.解:(1)连接OA,
∵△AOB的面积=△ABC的面积=3,△AOB的面积=|k|,
∴|k|=2,
∴k=±4;
又∵反比例函数的图象的一支位于第一象限,
∴k>0.
∴k=4.
∴这个反比例函数的解析式为y=;
(2)∵OB=BA,
∴设A(a,a),
∵反比例函数y=经过点A,
∴a2=4,
∴a=2,
∴A(2,2),
把y=1代入y=得,x=4,
∴P(4,1).
作点P关于x轴的对称点P′(4,﹣1),连接AP′与x轴交于点Q,此时QA+QP最小,
设过A,P′的直线表达式为y=mx+n,
∴,解得,
∴过A,P′的直线表达式为.
由,得.
∴点Q的坐标为.
23.解:(1)把A(,1)代入反比例函数y=得:k=1×=,
所以反比例函数的表达式为y=;
(2)∵A(,1),OA⊥AB,AB⊥x轴于C,
∴OC=,AC=1,
OA===2,
∵tanA==,
∴∠A=60°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠B=30°,
∴OB=2OC=2,
∴S△AOB===2,
∵S△AOP=S△AOB,
∴,
∵AC=1,
∴OP=2,
∴点P的坐标为(﹣2,0).
24.解:(1)如图1,过点A作AD⊥y轴于点D,则∠ADO=∠BOC=90°,
∴BO∥AD,
∴,
∵CB=AB,C(0,﹣8),
∴CO=DO=8,D(0,8),
∵S△OCB=S△OAB=8,
∴×CO×AD=S△OAC=16,
∴×8AD=16,
解得,AD=4,
∴A(4,8),
把A(4,8)代入y=,得8=,
解得,m=32,
把A(4,8)、C(0,﹣8)代入y=kx+b,
得,解得,
∴反比例函数与一次函数的解析式分别为y=和y=4x﹣8.
(2)如图2,设直线y=4x﹣8交双曲线y=的另一个交点是点E,
由得,或,
∴E(﹣2,﹣16),
由函数图象可知,当直线y=4x﹣8在双曲线y=的下方时,则x<﹣2
或0<x<4,
∴不等式kx+b<的解集是x<﹣2
或0<x<4,
由kx+b<得,kx+b﹣<0,
∴kx+b﹣<0的解集是x<﹣2
或0<x<4.
(3)如图3,设点P的坐标为(0,y),则PO=y,DP=8﹣y;
对于直线y=4x﹣8,当y=0时,由4x﹣8=0,得x=2,
∴B(2,0),
过点A作AD⊥y轴于点D,
则∠ADP=∠POB=∠APB=90°,
∴∠APD=90°﹣∠BPO=∠PBO,
∴△ADP∽△POB,
∴,
∴,
解得,y1=,y2=,
∴点P的坐标为(0,)或(0,).
