2021-2022学年八年级数学人教版上册14.2.1平方差公式同步习题(word版、含解析)
文档属性
| 名称 | 2021-2022学年八年级数学人教版上册14.2.1平方差公式同步习题(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 310.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 13:25:18 | ||
图片预览



文档简介
2021-2022学年八年级数学上册同步(人教版)
14.2.1平方差公式
时间:60分钟,
一、单选题
1.计算的结果是
A.2
B.
C.
D.1
2.下列多项式的乘法中用平方差公式计算的是
A.
B.
C.
D.
3.在下列计算中,不能用平方差公式计算的是(
)
A.
B.
C.
D.
4.下列各式中,不能用平方差公式计算的是(
)
A.(-x-y)(x-y)
B.(x-y)(-x+y)
C.(x+y)(-x+y)
D.(-x+y)(-x-y)
5.如果用平方差公式计算,则可将原式变形为(
)
A.
B.
C.
D.
6.若,,则的值为(
)
A.
B.
C.
D.2
7.在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是(
)
A.
B.
C.
D.
8.在边长为a的正方形中挖去一个边长为b的小正方形()(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A.
B.
C.
D.
二、填空题
9.一个正方形的面积为,如果边长增加,则面积增加了________.
10.计算:__________.
11.已知:且,则__.
12.已知,,则__.
13.计算:=__________.
14.____.
15.如图,从图①到图②的变化过程中可以发现的数学公式是_______.
16.某公园原来有一块长方形草坪,经规划后,南面要缩短12米,东面要加长12米,结果改造后的草坪刚好是一个边长为x米的正方形.则改造后草坪面积______(填“增加”或“减少”)了_____平方米.
三、解答题
17.
18.
19.(1)
(2)
20.已知三角形的底边是,高是,求这个三角形的面积.若,,则这个三角形的面积是多少?
21.先化简,再求值:,其中,.
22.图①所示是边长为的大正方形中有一个边长为的小正方形.图②是由图①中阴影部分拼成的一个长方形.
(1)设图①中阴影部分的面积为,图②中阴影部分的面积为,请用含的式子表示:
,
;(不必化简)
(2)以上结果可以验证的乘法公式是
;
(3)利用(2)中得到的公式,计算:.
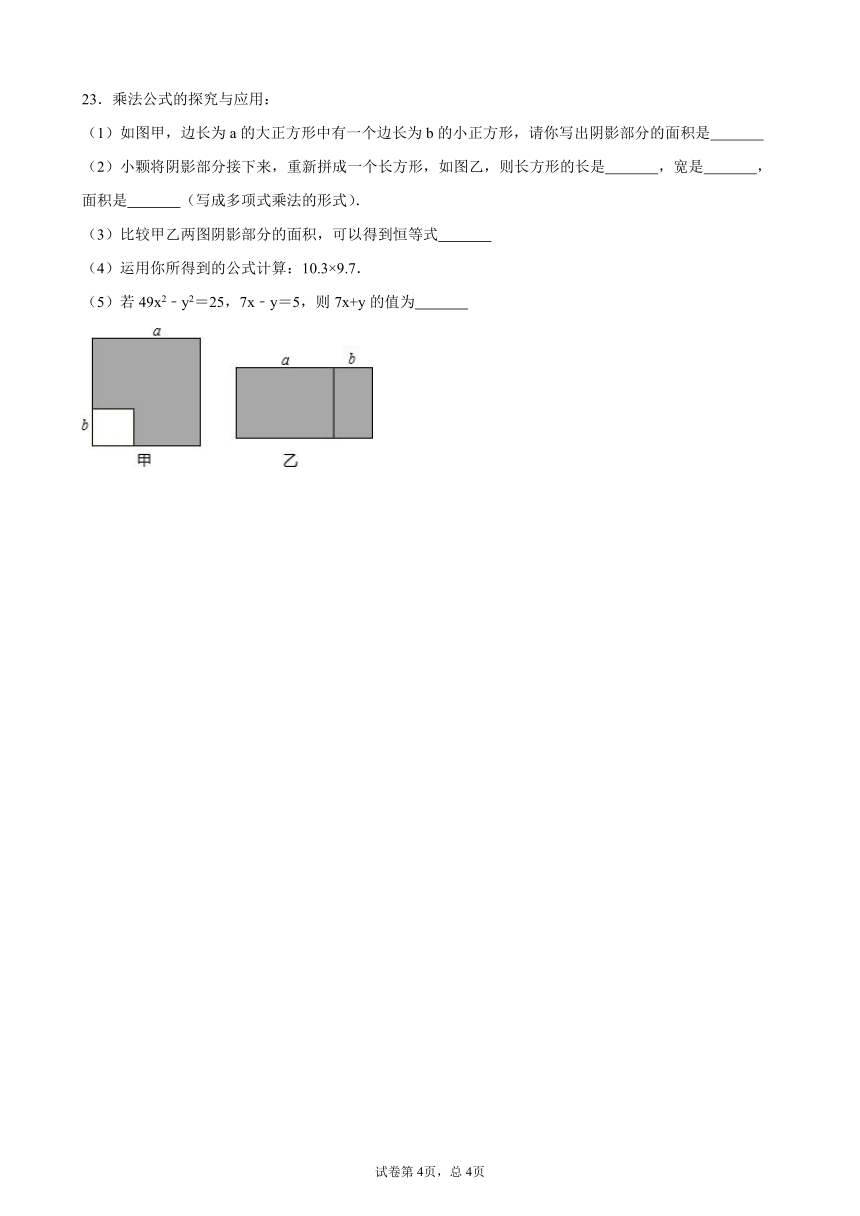
23.乘法公式的探究与应用:
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分的面积是
(2)小颗将阴影部分接下来,重新拼成一个长方形,如图乙,则长方形的长是
,宽是
,面积是
(写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到恒等式
(4)运用你所得到的公式计算:10.3×9.7.
(5)若49x2﹣y2=25,7x﹣y=5,则7x+y的值为
试卷第2页,总2页
参考答案
1.D
【解析】解:
.
故选:.
2.A
【解析】解:平方差公式的使用条件:两个二项式相乘,其中两项相同,两项互为相反数.
符合这个条件的只有.
故选:.
3.A
【解析】解:∵平方差公式为,
两个因式中都是两项式,一项相同,另一项互为相反数;
A.
两项都是互为相反数,不能用平方差公式计算,故选项A符合题意;
B.
两个因式中都是两项式,前项相同,后项互为相反数,,能用平方差公式计算,故选项B不符合题意;
C.
两个因式中都是两项式,后项相同,前项互为相反数能用平方差公式计算,故选项C不符合题意;
D.
两个因式中都是两项式,把第二个括号中利用加法交换律换位,前一项相同,后一项互为相反数,可以用平方差公式计算,故选项D不符合题意.
故选择A.
4.B
【解析】解:A、符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意;
B、不符合平方差公式的特点,不能用平方差公式进行计算,故本选项符合题意.
C、符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意;
D、符合平方差公式的特点,能用平方差公式进行计算,故本选项不符合题意.
故选:B.
5.C
【解析】,
故选:.
6.B
【解析】∵,
∴,
∴.
故选:B.
7.A
【解析】左阴影的面积,
右平行四边形的面积,
两面积相等所以等式成立.
这是平方差公式.
故选:A.
8.A
【解析】甲图中阴影部分的面积为大正方形的面积减去小正方形的面积,即,乙图中阴影部分长方形的长为,宽为,阴影部分的面积为,根据两个图形中阴影部分的面积相等可得.
故选:A.
9.
【解析】解:∵原正方形的面积为a2cm2,
∴边长为acm,
∴增加后的边长是(a+1)cm,
∴增加的面积=(a+1)2-a2=(a+1+a)(a+1-a)=2a+1.
故答案为:(2a+1).
10.4041
【解析】解:
=
=
=4041
故答案为:4041.
11.
【解析】解:,,
.
故答案为:.
12.2
【解析】解:,,
,即.
.
故答案是:2.
13.
【解析】
.
故答案为:.
14.
【解析】200.5×199.5=(200+0.5)×(200?0.5)=2002?0.52=40000?0.25=39999.75.
故答案为:39999.75.
15.(a+b)(a-b)=a2-b2
【解析】∵图①的面积为(a+b)(a-b),图②的面积为a2-b2,
∴(a+b)(a-b)=a2-b2.
16.增加
144
【解析】由题意知,公园原来的草坪长为(x+12)米,宽为(x-12)米,
∴原来草坪面积为:(x+12)(x-12)=
x2-144(平方米),
∵改造后的面积是x2平方米,
∴改造后草坪面积增加了,增加了144平方米.
故答案为:增加;144.
17.
【解析】解:原式=
=
=
=.
18.
【解析】解:原式
19.(1)
(2)
【解析】解:原式
原式
20.,
【解析】由面积公式求得面积为××
=×
=,
将、代入原式==18-4.5=.
故这个三角形的面积是.
21.,1.
【解析】解:,
,
,
,
当,时,
原式.
22.(1),(2)
;(3)1.
【解析】解:(1)大正方形的面积为a2,小正方形的面积为b2,
故图1阴影部分的面积值为a2-b2;
图2长方形的长和宽分别为(a+b)、(a-b),
故图2重拼的长方形的面积为(a+b)(a-b);
故答案为:a2-b2,(a+b)(a-b);
(2)比较上面的结果,都表示同一阴影的面积,它们相等,
即(a+b)(a-b)=a2-b2,可以验证平方差公式,这也是平方差公式的几何意义;
故答案为:(a+b)(a-b)=a2-b2;
(3)
.
23.(1)a2﹣b2;(2)a+b,a﹣b,(a+b)(a﹣b);(3)(a+b)(a﹣b)=a2﹣b2;(4)99.91;(5)5
【解析】解:(1)阴影部分的面积=大正方形的面积﹣小正方形的面积=a2﹣b2
故答案为:a2﹣b2.
(2)长方形的长是(a+b),宽是(a﹣b),面积=长×宽=(a+b)(a﹣b)
故答案为:a+b;a﹣b;(a+b)(a﹣b).
(3)由(1)(2)可得(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
(4)10.3×9.7
=(10+0.3)(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91
(5)∵49x2﹣y2=25,
∴(7x+y)(7x﹣y)=25
∵7x﹣y=5
∴(7x+y)×5=25
∴7x+y=5
故答案为:5.
答案第1页,总2页
答案第1页,总2页
14.2.1平方差公式
时间:60分钟,
一、单选题
1.计算的结果是
A.2
B.
C.
D.1
2.下列多项式的乘法中用平方差公式计算的是
A.
B.
C.
D.
3.在下列计算中,不能用平方差公式计算的是(
)
A.
B.
C.
D.
4.下列各式中,不能用平方差公式计算的是(
)
A.(-x-y)(x-y)
B.(x-y)(-x+y)
C.(x+y)(-x+y)
D.(-x+y)(-x-y)
5.如果用平方差公式计算,则可将原式变形为(
)
A.
B.
C.
D.
6.若,,则的值为(
)
A.
B.
C.
D.2
7.在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是(
)
A.
B.
C.
D.
8.在边长为a的正方形中挖去一个边长为b的小正方形()(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A.
B.
C.
D.
二、填空题
9.一个正方形的面积为,如果边长增加,则面积增加了________.
10.计算:__________.
11.已知:且,则__.
12.已知,,则__.
13.计算:=__________.
14.____.
15.如图,从图①到图②的变化过程中可以发现的数学公式是_______.
16.某公园原来有一块长方形草坪,经规划后,南面要缩短12米,东面要加长12米,结果改造后的草坪刚好是一个边长为x米的正方形.则改造后草坪面积______(填“增加”或“减少”)了_____平方米.
三、解答题
17.
18.
19.(1)
(2)
20.已知三角形的底边是,高是,求这个三角形的面积.若,,则这个三角形的面积是多少?
21.先化简,再求值:,其中,.
22.图①所示是边长为的大正方形中有一个边长为的小正方形.图②是由图①中阴影部分拼成的一个长方形.
(1)设图①中阴影部分的面积为,图②中阴影部分的面积为,请用含的式子表示:
,
;(不必化简)
(2)以上结果可以验证的乘法公式是
;
(3)利用(2)中得到的公式,计算:.
23.乘法公式的探究与应用:
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分的面积是
(2)小颗将阴影部分接下来,重新拼成一个长方形,如图乙,则长方形的长是
,宽是
,面积是
(写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到恒等式
(4)运用你所得到的公式计算:10.3×9.7.
(5)若49x2﹣y2=25,7x﹣y=5,则7x+y的值为
试卷第2页,总2页
参考答案
1.D
【解析】解:
.
故选:.
2.A
【解析】解:平方差公式的使用条件:两个二项式相乘,其中两项相同,两项互为相反数.
符合这个条件的只有.
故选:.
3.A
【解析】解:∵平方差公式为,
两个因式中都是两项式,一项相同,另一项互为相反数;
A.
两项都是互为相反数,不能用平方差公式计算,故选项A符合题意;
B.
两个因式中都是两项式,前项相同,后项互为相反数,,能用平方差公式计算,故选项B不符合题意;
C.
两个因式中都是两项式,后项相同,前项互为相反数能用平方差公式计算,故选项C不符合题意;
D.
两个因式中都是两项式,把第二个括号中利用加法交换律换位,前一项相同,后一项互为相反数,可以用平方差公式计算,故选项D不符合题意.
故选择A.
4.B
【解析】解:A、符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意;
B、不符合平方差公式的特点,不能用平方差公式进行计算,故本选项符合题意.
C、符合平方差公式的特点,能用平方差公式计算,故本选项不符合题意;
D、符合平方差公式的特点,能用平方差公式进行计算,故本选项不符合题意.
故选:B.
5.C
【解析】,
故选:.
6.B
【解析】∵,
∴,
∴.
故选:B.
7.A
【解析】左阴影的面积,
右平行四边形的面积,
两面积相等所以等式成立.
这是平方差公式.
故选:A.
8.A
【解析】甲图中阴影部分的面积为大正方形的面积减去小正方形的面积,即,乙图中阴影部分长方形的长为,宽为,阴影部分的面积为,根据两个图形中阴影部分的面积相等可得.
故选:A.
9.
【解析】解:∵原正方形的面积为a2cm2,
∴边长为acm,
∴增加后的边长是(a+1)cm,
∴增加的面积=(a+1)2-a2=(a+1+a)(a+1-a)=2a+1.
故答案为:(2a+1).
10.4041
【解析】解:
=
=
=4041
故答案为:4041.
11.
【解析】解:,,
.
故答案为:.
12.2
【解析】解:,,
,即.
.
故答案是:2.
13.
【解析】
.
故答案为:.
14.
【解析】200.5×199.5=(200+0.5)×(200?0.5)=2002?0.52=40000?0.25=39999.75.
故答案为:39999.75.
15.(a+b)(a-b)=a2-b2
【解析】∵图①的面积为(a+b)(a-b),图②的面积为a2-b2,
∴(a+b)(a-b)=a2-b2.
16.增加
144
【解析】由题意知,公园原来的草坪长为(x+12)米,宽为(x-12)米,
∴原来草坪面积为:(x+12)(x-12)=
x2-144(平方米),
∵改造后的面积是x2平方米,
∴改造后草坪面积增加了,增加了144平方米.
故答案为:增加;144.
17.
【解析】解:原式=
=
=
=.
18.
【解析】解:原式
19.(1)
(2)
【解析】解:原式
原式
20.,
【解析】由面积公式求得面积为××
=×
=,
将、代入原式==18-4.5=.
故这个三角形的面积是.
21.,1.
【解析】解:,
,
,
,
当,时,
原式.
22.(1),(2)
;(3)1.
【解析】解:(1)大正方形的面积为a2,小正方形的面积为b2,
故图1阴影部分的面积值为a2-b2;
图2长方形的长和宽分别为(a+b)、(a-b),
故图2重拼的长方形的面积为(a+b)(a-b);
故答案为:a2-b2,(a+b)(a-b);
(2)比较上面的结果,都表示同一阴影的面积,它们相等,
即(a+b)(a-b)=a2-b2,可以验证平方差公式,这也是平方差公式的几何意义;
故答案为:(a+b)(a-b)=a2-b2;
(3)
.
23.(1)a2﹣b2;(2)a+b,a﹣b,(a+b)(a﹣b);(3)(a+b)(a﹣b)=a2﹣b2;(4)99.91;(5)5
【解析】解:(1)阴影部分的面积=大正方形的面积﹣小正方形的面积=a2﹣b2
故答案为:a2﹣b2.
(2)长方形的长是(a+b),宽是(a﹣b),面积=长×宽=(a+b)(a﹣b)
故答案为:a+b;a﹣b;(a+b)(a﹣b).
(3)由(1)(2)可得(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
(4)10.3×9.7
=(10+0.3)(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91
(5)∵49x2﹣y2=25,
∴(7x+y)(7x﹣y)=25
∵7x﹣y=5
∴(7x+y)×5=25
∴7x+y=5
故答案为:5.
答案第1页,总2页
答案第1页,总2页
