2021-2022学年人教版九年级数学上册22.3实际问题与二次函数 同步能力达标训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册22.3实际问题与二次函数 同步能力达标训练(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 475.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 13:34:06 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学上册《22.3实际问题与二次函数》
同步能力达标训练(附答案)
一、选择题
1.如图,点E、F、G、H分别是正方形ABCD边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能为( )
A.B.C.D.
2.某涵洞的截面是抛物线形状,如图所示的平面直角坐标系中,抛物线对应的函数解析式为y=﹣x2,当涵洞水面宽AB为16m时,涵洞顶点O至水面的距离为( )
A.﹣6m
B.12m
C.16m
D.24m
3.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面上升1.5m,水面宽度为( )
A.1m
B.2m
C.m
D.m
4.学校组织学生去南京进行研学实践活动,小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且a=﹣.洗手液瓶子的截面图下部分是矩形CGHD.小王同学测得:洗手液瓶子的底面直径GH=12cm,喷嘴位置点B距台面的距离为16cm,且B、D、H三点共线.小王在距离台面15.5cm处接洗手液时,手心Q到直线DH的水平距离为3cm,若小王不去接,则洗手液落在台面的位置距DH的水平距离是( )cm.
A.12
B.12
C.6
D.6
5.如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(﹣1,﹣2)、(1,﹣2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( )
A.﹣3
B.﹣1
C.1
D.3
6.定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).下表记录了该同学将篮球投出后的x与y的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为( )
x(单位:m)
0
2
4
y(单位:m)
2.25
3.45
3.05
A.1.5m
B.2m
C.2.5m
D.3m
7.从地面竖直向上先后抛出两个小球,小球的高度h(米)与运动时间t(秒)之间的函数关系式为h=﹣(t﹣3)2+40,若后抛出的小球经过2.5秒比先抛出的小球高米,则抛出两个小球的间隔时间是( )
A.1秒
B.1.5秒
C.2秒
D.2.5秒
8.若二次函数y=x2﹣2x+k的图象经过点(﹣1,y1),(,y2),则y1与y2的大小关系为( )A.y1>y2
B.y1=y2
C.y1<y2
D.不能确定
9.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为:P=at2+bt+c(a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
10.某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.则最大利润是( )
A.180
B.220
C.190
D.200
11.某广场有一个小型喷泉,水流从垂直于地面的水管OA喷出,OA长为1.5m.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为3m.建立平面直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间近似满足函数关系y=ax2+x+c(a≠0),则水流喷出的最大高度为( )
A.1米
B.米
C.2米
D.米
12.抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A.5
B.4
C.3
D.2
二、填空题
13.扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,设与墙垂直的一边为xcm,则矩形面积s随之x变化的函数解析式为
.
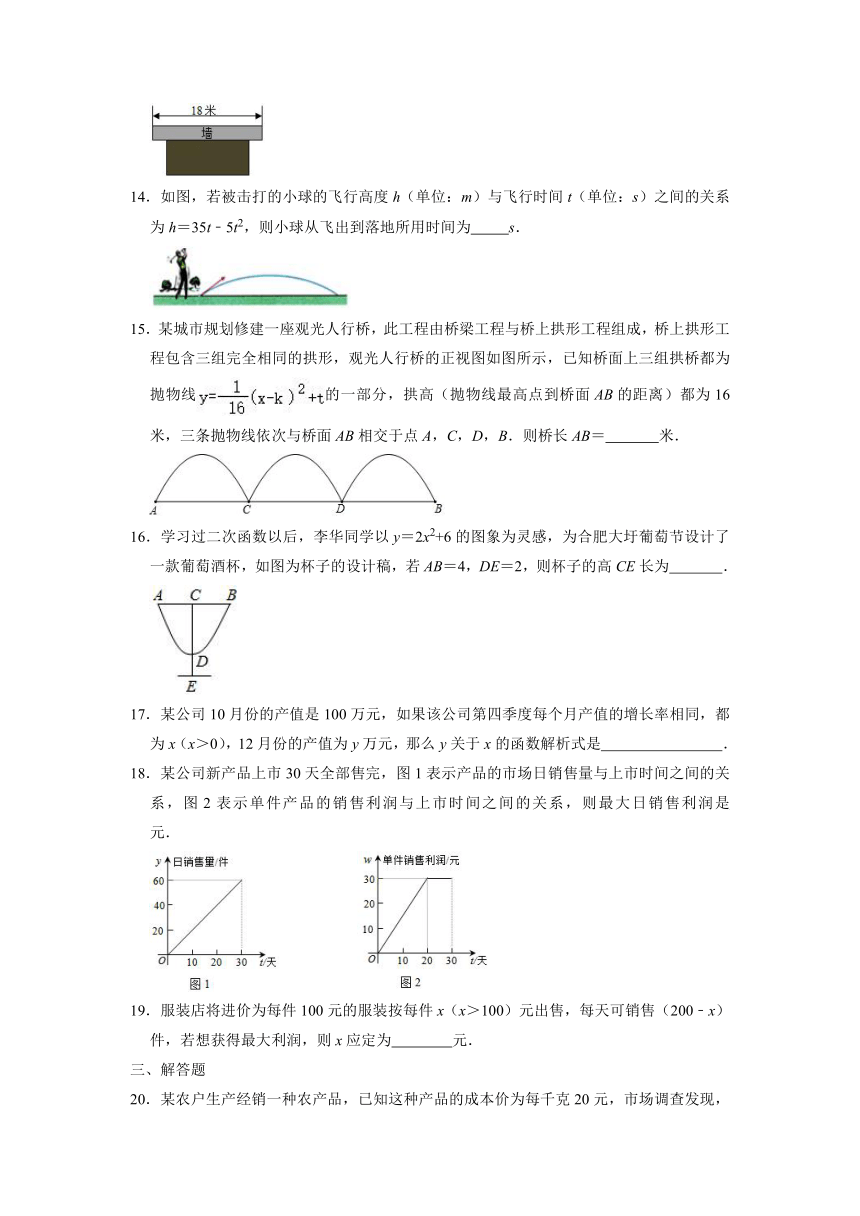
14.如图,若被击打的小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的关系为h=35t﹣5t2,则小球从飞出到落地所用时间为
s.
15.某城市规划修建一座观光人行桥,此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的正视图如图所示,已知桥面上三组拱桥都为抛物线的一部分,拱高(抛物线最高点到桥面AB的距离)都为16米,三条抛物线依次与桥面AB相交于点A,C,D,B.则桥长AB=
米.
16.学习过二次函数以后,李华同学以y=2x2+6的图象为灵感,为合肥大圩葡萄节设计了一款葡萄酒杯,如图为杯子的设计稿,若AB=4,DE=2,则杯子的高CE长为
.
17.某公司10月份的产值是100万元,如果该公司第四季度每个月产值的增长率相同,都为x(x>0),12月份的产值为y万元,那么y关于x的函数解析式是
.
18.某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是
元.
19.服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为
元.
三、解答题
20.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.并指出该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(2)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
21.某实验器材专营店为迎接我县理化实验操作中考,购进一批电学实验盒子,一台电学实验盒子的成本是30元,当售价定为每台50元时,每天可卖出20台,但由于电学实验盒子是特殊时期的销售产品,专营店准备对它进行降价销售,根据以往经验,每台售价每降低3元,每天的销售量增加6台.设每台降低了x(元),每天销售量为y(台).
(1)求y与x之间的函数表达式(不用写出x的取值范围);
(2)每天的利润用w(元)表示,当每台降低多少元时获得最大利润,最大利润是多少?
22.在平面直角坐标系中,将一块等腰直角三角板(△ABC)按如图所示放置,若AO=2,OC=1,∠ACB=90°.
(1)直接写出B点的坐标是
;
(2)如果抛物线l:y=ax2﹣ax﹣2经过点B,试求抛物线l的解析式;
(3)把△ABC绕着点C逆时针旋转90°后,顶点A的对应点A1是否在抛物线l上?为什么?
23.如图,在平面直角坐标系中,点A,B分别是y轴正半轴和x轴负半轴上的两个点,O为原点,OA=3,OB=1,将Rt△ABC绕点O顺时针旋转90°得到Rt△COD,抛物线y=﹣x2+bx+c经过A,B,C三点.
(1)求此抛物线的解析式及顶点P的坐标;
(2)若直线l:y=﹣x+4与抛物线交于M,N两点,求△PMN面积;
(3)抛物线的对称轴上是否存在一点Q,使得△DCQ为直角三角形?若存在,请直接写出求点Q的坐标;若不存在,请说明理由.
24.如图,二次函数y=﹣x2+(k﹣1)x+4的图象与y轴交于点A,与x轴的负半轴交于点B,且△AOB的面积为6.
(1)求A,B两点的坐标;
(2)求该二次函数的表达式;
(3)如果点P在坐标轴上,且△ABP是等腰三角形,直接写出P点坐标.
25.如图①,直线y=kx+2与抛物线y=x2+bx+c相交于在x轴和y轴上的B、C两点,OB=6,D为抛物线的顶点.M是线段BC上的一动点(M与B、C不重合),过M作MN⊥x轴,交抛物线于点N.
(1)k=
;b=
.
(2)求MN的最大值.
(3)如图②,若M是线段BC的中点,P是抛物线上的一动点,且点P在直线MN的右侧,连接PM、PC,当△PCM的面积是时,求此时点P的坐标.
参考答案
1.解:设正方形的边长为m,则m>0,
∵AE=x,
∴DH=x,
∴AH=m﹣x,
∵EH2=AE2+AH2,
∴y=x2+(m﹣x)2,
y=x2+x2﹣2mx+m2,
y=2x2﹣2mx+m2,
=2[(x﹣m)2+],
=2(x﹣m)2+m2,
∴y与x的函数图象是A.
故选:A.
2.解:依题意,设A点坐标为(﹣8,y),
代入抛物线方程得:y=﹣×64=﹣16,
即水面到桥拱顶点O的距离为16米.
故选:C.
3.解:如右图建立平面直角坐标系,
设抛物线的解析式为y=ax2,
由已知可得,点(2,﹣2)在此抛物线上,
则﹣2=a×22,
解得a=﹣,
∴y=﹣x2,
当y=﹣0.5时,﹣x2=﹣0.5,
解得x=±1,
此时水面的宽度为2m,
故选:B.
4.解:根据题意:
GH所在直线为x轴,GH的垂直平分线所在直线为y轴建立如图所示的平面直角坐标系,
喷口B为抛物线顶点,共线的三点B、D、H所在直线为抛物线的对称轴,
根据题意,Q(9,15.5),B(6,16),OH=6,
设抛物线解析式为
y=ax2+bx+c,
∵a=﹣,
将Q点和B点坐标代入,
得系数b=,c=14,
所以抛物线解析式为:
y=﹣x2+x+14.
符号题意:洗手液从喷口B流出,路线近似呈抛物线状,
当y=0时,即0=﹣x2+x+14,
解得:x=6+12(负值舍去),
所以洗手液落在台面的位置距DH的水平距离是12cm.
故选:B.
5.解:根据题意知,点B的横坐标的最大值为3,
即可知当对称轴过N点时,点B的横坐标最大,
此时的A点坐标为(﹣1,0),
当可知当对称轴过M点时,点A的横坐标最小,此时的B点坐标为(1,0),
此时A点的坐标最小为(﹣3,0),
故点A的横坐标的最小值为﹣3,
故选:A.
6.解:设二次函数的解析式为y=ax2+bx+c,
根据表可得:,
解得:,
∴y=﹣0.2x2+x+2.25=﹣0.2(x﹣2.5)2+3.5,
∴可推断出篮球飞行到最高点时,水平距离为2.5米,
故选:C.
7.解:2.5秒时,后球的高度为:
h2=﹣(2.5﹣3)2+40=,
则此时,前球的高度为h1=﹣=,
令﹣(t﹣3)2+40=,整理得(t﹣3)2=1,
∴t1=4,t2=2(舍),
△t=4﹣2.5=1.5.
故选:B.
8.解:当x=﹣1时,y1=x2﹣2x+k=1+2+k=k+3;
当x=时,y2=x2﹣2x+k=﹣1+k=k﹣,
所以y1>y2.
故选:A.
9.解:将图象中的三个点(3,0.8)、(4,0.9)、(5,0.6)代入函数关系P=at2+bt+c中,
,
解得,
所以函数关系式为:P=﹣0.2t2+1.5t﹣1.9,
由题意可知:加工煎炸臭豆腐的最佳时间为抛物线顶点的横坐标:
t=﹣=﹣=3.75,
则当t=3.75分钟时,可以得到最佳时间.
故选:C.
10.解:设y=kx+b,由图象可知,,
解之,得:,
∴y=﹣2x+60;
设销售利润为p,根据题意得,p=(x﹣10)y
=(x﹣10)(﹣2x+60)
=﹣2x2+80x﹣600,
∵a=﹣2<0,
∴p有最大值,
当x=﹣=20时,p最大值=200.
即当销售单价为20元/千克时,每天可获得最大利润200元,
故选:D.
11.解:由题意可得,抛物线经过点(0,1.5)和(3,0),
把上述两个点坐标代入二次函数表达式得:
,
解得:,
∴函数表达式为:y=﹣x2+x+,
=﹣(x﹣1)2+2,
∵a<0,故函数有最大值,
∴当x=1时,y取得最大值,此时y=2,
答:水流喷出的最大高度为2米.
故选:C.
12.解:①∵二次函数与x轴交于点A(﹣1,0)、B(3,0).
∴二次函数的对称轴为直线x==1,即﹣=1,
∴2a+b=0.
故①正确;
②∵二次函数y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0).
∴a﹣b+c=0,9a+3b+c=0.
又∵b=﹣2a.
∴3b=﹣6a,a﹣(﹣2a)+c=0.
∴3b=﹣6a,2c=﹣6a.
∴2c=3b.
故②错误;
③∵抛物线开口向上,对称轴是直线x=1.
∴x=1时,二次函数有最小值.
∴m≠1时,a+b+c<am2+bm+c.
即a+b<am2+bm.
故③正确;
④∵AD=BD,AB=4,△ABD是等腰直角三角形.
∴AD2+BD2=42.
解得,AD2=8.
设点D坐标为(1,y).
则[1﹣(﹣1)]2+y2=AD2.
解得y=±2.
∵点D在x轴下方.
∴点D为(1,﹣2).
∵二次函数的顶点D为(1,﹣2),过点A(﹣1,0).
设二次函数解析式为y=a(x﹣1)2﹣2.
∴0=a(﹣1﹣1)2﹣2.
解得a=.
故④正确;
⑤由图象可得,AC≠BC.
故△ABC是等腰三角形时,a的值有2个.(故⑤错误)
故①③④正确,②⑤错误.
故选:C.
13.解:由题意可得,
s=x(30﹣2x)=﹣2x2+30x,
故答案为:s=﹣2x2+30x
14.解:依题意,令h=0得0=35t﹣5t2,
得t(35﹣5t)=0,
解得t=0(舍去)或t=7,
即小球从飞出到落地所用的时间为7s.
故答案为7.
15.解:如图,以线段AC的中垂线为y轴,AB为x轴,建立平面直角坐标系,
则抛物线AC的顶点坐标为(0,16),
所以抛物线解析式为y=﹣x2+16,
当y=0时,x1=16,x2=﹣16,
∴点A的坐标为(﹣16,0),点C的坐标为(16,0),
∴AC=16﹣(﹣16)=16+16=32,
∴AB=3AC=96,
即桥长AB为96米;
故答案为:96.
16.解:建立如图所示的平面直角坐标系,
由题意可得:D点坐标为:(0,6),
∵AB=4,
∴B点的横坐标为:2,
故x=2时,y=2×4+6=14,
即B(2,14),
则DC=14﹣6=8,
故CE=DC+DE=8+2=10,
故答案为:10.
17.解:由题意可得,
y=100(1+x)2,
故答案为:y=100(1+x)2.
18.解:设日销售量y与上市时间t之间的函数关系式为y=kt,
30k=60,得k=2,
即日销售量y与上市时间t之间的函数关系式为y=2t,
当0<t≤20时,设单件的利润w与t之间的函数关系式为w=at,
20a=30,得a=1.5,
即当0<t≤20时,单件的利润w与t之间的函数关系式为w=1.5t,
当20<t≤30时,单件的利润w与t之间的函数关系式为w=30,
设日销售利润为W元,
当0<t≤20时,W=1.5t×2t=3t2,
故当t=20时,W取得最大值,此时W=1200,
当20<t≤30时,W=30×2t=60t,
故当t=30时,W取得最大值,此时W=1800,
综上所述,最大日销售利润为1800元,
故答案为:1800.
19.解:设获得的利润为y元,由题意得:
y=(x﹣100)(200﹣x)
=﹣x2+300x﹣20000
=﹣(x﹣150)2+2500
∵a=﹣1<0
∴当x=150元时,y取得最大值2500元,
故答案为150.
20.解:(1)根据题意得,w=(x﹣20)(﹣2x+80)=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∴当x=30时,每天的利润最大,最大利润为200元;
(2)令﹣2(x﹣30)2+200=150,
解得:x=35或x=25,
∵这种产品的销售价不高于每千克28元,
∴x=25,
答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元.
21.解:(1)由题意可得,y=20+×6=20+2x,
∴y与x之间的函数表达式是y=2x+20;
(2)由题意得,w=(50﹣30﹣x)(20+2x)=(20﹣x)(20+2x)=﹣2(x﹣5)2+450,
当x=5时,w有最大值450,
∴当售价为45元,利润最大为450元,
即当每台降低5元时获得最大利润,最大利润是450元.
22.解:(1)如图1,过点B作BD⊥x轴,垂足为D,
∵∠BCD+∠ACO=90°,∠AC0+∠OAC=90°,
∴∠BCD=∠CAO,
又∵∠BDC=∠COA=90°,CB=AC,
在△BDC和△COA中,
,
∴△BDC≌△COA(AAS),
∴BD=OC=1,CD=OA=2,
∴点B的坐标为(3,1),
故答案为(3,1);
(2)∵抛物线y=ax2﹣ax﹣2过点B(3,1),
∴1=9a﹣3a﹣2,
解得:a=,
∴抛物线的解析式为y=x2﹣x﹣2;
(3)A1在抛物线l上,理由:
旋转后如图2所示,过点A1作A1M⊥x轴,
∵把△ABC绕着点C逆时针旋转90°,
∴∠ABC=∠A1BC=90°,
∴A1,B,C共线,
在三角形BDC和三角形A1CM中,
,
∴△BDC≌△A1CM(AAS),
∴CM=CD=3﹣1=2,A1M=BD=1,
∴OM=1,
∴点A1(﹣1,﹣1),
把点x=﹣1代入y=x2﹣x﹣2,
y=﹣1,
∴点A1在抛物线上.
23.解:(1)Rt△ABC绕点O顺时针旋转90°得到Rt△COD,
则OD=OB=1,OC=OA=3,
故点A、B、C、D的坐标分别为(0,3)、(﹣1,0)、(3,0)、(0,1),
将点A、B的坐标代入抛物线表达式得,解得,
故抛物线的表达式为y=﹣x2+2x+3,
抛物线的对称轴为x=1,则点P(1,4);
(2)由,解得,
故点M、N的坐标分别为(,)、(2,3);
由y=﹣x+4知,当x=1时,y=,
设直线y=﹣x+4与对称轴x=1交于点F,则点F(1,),
S△PMN=S△PFM+S△PFN=×PF×(xN﹣xM)=×(4﹣)×(2﹣)=;
(3)存在,理由:
设点Q的坐标为(1,t),
则CD2=10,CQ2=22+t2,DQ2=12+(t﹣1)2,
当∠DQC为直角时,则10=22+t2+12+(t﹣1)2,解得t=﹣1或2;
当∠QDC为直角时,同理可得:t=4;
当∠DCQ为直角时,同理可得:t=﹣6,
故点Q的坐标为(1,﹣1)或(1,2)或(1,4)或(1,﹣6).
24.解:(1)由解析式可知,点A的坐标为(0,4),
∵S△OAB=×BO×4=6,
BO=3.所以B(3,0)或(﹣3,0),
∵二次函数与x轴的负半轴交于点B,
∴点B的坐标为(﹣3,0);
(2)把点B的坐标(﹣3,0)代入y=﹣x2+(k﹣1)x+4,
得﹣(﹣3)2+(k﹣1)×(﹣3)+4=0.
解得k﹣1=﹣,
∴所求二次函数的解析式为y=﹣x2﹣x+4;
(3)(Ⅰ)当点P在x轴上时,
①如图1,当AB=AP时,
则点P和点B关于y轴对称,
则点P的坐标为(3,0);
②如图2,当AB=BP时,
当点P在y轴左侧时,BP=AB=5,则OP=PB+OB=5+3=8,故点P(﹣8,0),
当点P在y轴右侧时,则BP′=5,过点P′(2,0),
点P的坐标为(2,0)或(﹣8,0);
③如图3,当AP=BP时,
设点P的坐标为(x,0),
根据题意,得=|x+3|.
解得x=.
∴点P的坐标为(,0);
故点P的坐标为(3,0),(2,0),(﹣8,0),(,0).
(Ⅱ)当点P在y轴上时,
同理可得,点P的坐标为(0,)或(0,9)或(0,﹣1)或(0,﹣4);
综上所述,点P的坐标为(3,0),(2,0),(﹣8,0),(,0)或(0,)或(0,9)或(0,﹣1)或(0,﹣4).
25.解:(1)∵OB=6,则点B(6,0),
将点B的坐标代入y=kx+2得,0=6k+2,解得k=﹣,
故一次函数表达式为y=﹣x+2,
令x=0,则y=2,故点C(0,2),则c=2,
故抛物线的表达式为y=x2+bx+2,
将点B的坐标代入上式并解得b=﹣,
故抛物线的表达式为y=x2﹣x+2,
故答案为﹣,﹣;
(2)设点N(x,x2﹣x+2),则点M(x,﹣x+2),
则MN=(﹣x+2)﹣(x2﹣x+2)=﹣x2+2x,
∵﹣<0,故MN有最大值,
当x=3时,MM的最大值为3;
(3)设点P(m,m2﹣m+2),
而点C(0,2),设直线CP交MN于点H,
由点PC的坐标得,直线PC的表达式为y=(m﹣7)x+2,
当x=3时,y=(m﹣7)x+2=m﹣5,即点H(3,m﹣5),
△PCM的面积=S△HMC+S△HMP=×MH×xP=×(m﹣5﹣1)×m=,
解得m=9或﹣3
∵点P在MN的右侧,故m>3,故舍去﹣3,
故点P的坐标为(9,8).
同步能力达标训练(附答案)
一、选择题
1.如图,点E、F、G、H分别是正方形ABCD边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能为( )
A.B.C.D.
2.某涵洞的截面是抛物线形状,如图所示的平面直角坐标系中,抛物线对应的函数解析式为y=﹣x2,当涵洞水面宽AB为16m时,涵洞顶点O至水面的距离为( )
A.﹣6m
B.12m
C.16m
D.24m
3.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面上升1.5m,水面宽度为( )
A.1m
B.2m
C.m
D.m
4.学校组织学生去南京进行研学实践活动,小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且a=﹣.洗手液瓶子的截面图下部分是矩形CGHD.小王同学测得:洗手液瓶子的底面直径GH=12cm,喷嘴位置点B距台面的距离为16cm,且B、D、H三点共线.小王在距离台面15.5cm处接洗手液时,手心Q到直线DH的水平距离为3cm,若小王不去接,则洗手液落在台面的位置距DH的水平距离是( )cm.
A.12
B.12
C.6
D.6
5.如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(﹣1,﹣2)、(1,﹣2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( )
A.﹣3
B.﹣1
C.1
D.3
6.定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).下表记录了该同学将篮球投出后的x与y的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为( )
x(单位:m)
0
2
4
y(单位:m)
2.25
3.45
3.05
A.1.5m
B.2m
C.2.5m
D.3m
7.从地面竖直向上先后抛出两个小球,小球的高度h(米)与运动时间t(秒)之间的函数关系式为h=﹣(t﹣3)2+40,若后抛出的小球经过2.5秒比先抛出的小球高米,则抛出两个小球的间隔时间是( )
A.1秒
B.1.5秒
C.2秒
D.2.5秒
8.若二次函数y=x2﹣2x+k的图象经过点(﹣1,y1),(,y2),则y1与y2的大小关系为( )A.y1>y2
B.y1=y2
C.y1<y2
D.不能确定
9.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为:P=at2+bt+c(a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
10.某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.则最大利润是( )
A.180
B.220
C.190
D.200
11.某广场有一个小型喷泉,水流从垂直于地面的水管OA喷出,OA长为1.5m.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为3m.建立平面直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间近似满足函数关系y=ax2+x+c(a≠0),则水流喷出的最大高度为( )
A.1米
B.米
C.2米
D.米
12.抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A.5
B.4
C.3
D.2
二、填空题
13.扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,设与墙垂直的一边为xcm,则矩形面积s随之x变化的函数解析式为
.
14.如图,若被击打的小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的关系为h=35t﹣5t2,则小球从飞出到落地所用时间为
s.
15.某城市规划修建一座观光人行桥,此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的正视图如图所示,已知桥面上三组拱桥都为抛物线的一部分,拱高(抛物线最高点到桥面AB的距离)都为16米,三条抛物线依次与桥面AB相交于点A,C,D,B.则桥长AB=
米.
16.学习过二次函数以后,李华同学以y=2x2+6的图象为灵感,为合肥大圩葡萄节设计了一款葡萄酒杯,如图为杯子的设计稿,若AB=4,DE=2,则杯子的高CE长为
.
17.某公司10月份的产值是100万元,如果该公司第四季度每个月产值的增长率相同,都为x(x>0),12月份的产值为y万元,那么y关于x的函数解析式是
.
18.某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是
元.
19.服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为
元.
三、解答题
20.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.并指出该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(2)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
21.某实验器材专营店为迎接我县理化实验操作中考,购进一批电学实验盒子,一台电学实验盒子的成本是30元,当售价定为每台50元时,每天可卖出20台,但由于电学实验盒子是特殊时期的销售产品,专营店准备对它进行降价销售,根据以往经验,每台售价每降低3元,每天的销售量增加6台.设每台降低了x(元),每天销售量为y(台).
(1)求y与x之间的函数表达式(不用写出x的取值范围);
(2)每天的利润用w(元)表示,当每台降低多少元时获得最大利润,最大利润是多少?
22.在平面直角坐标系中,将一块等腰直角三角板(△ABC)按如图所示放置,若AO=2,OC=1,∠ACB=90°.
(1)直接写出B点的坐标是
;
(2)如果抛物线l:y=ax2﹣ax﹣2经过点B,试求抛物线l的解析式;
(3)把△ABC绕着点C逆时针旋转90°后,顶点A的对应点A1是否在抛物线l上?为什么?
23.如图,在平面直角坐标系中,点A,B分别是y轴正半轴和x轴负半轴上的两个点,O为原点,OA=3,OB=1,将Rt△ABC绕点O顺时针旋转90°得到Rt△COD,抛物线y=﹣x2+bx+c经过A,B,C三点.
(1)求此抛物线的解析式及顶点P的坐标;
(2)若直线l:y=﹣x+4与抛物线交于M,N两点,求△PMN面积;
(3)抛物线的对称轴上是否存在一点Q,使得△DCQ为直角三角形?若存在,请直接写出求点Q的坐标;若不存在,请说明理由.
24.如图,二次函数y=﹣x2+(k﹣1)x+4的图象与y轴交于点A,与x轴的负半轴交于点B,且△AOB的面积为6.
(1)求A,B两点的坐标;
(2)求该二次函数的表达式;
(3)如果点P在坐标轴上,且△ABP是等腰三角形,直接写出P点坐标.
25.如图①,直线y=kx+2与抛物线y=x2+bx+c相交于在x轴和y轴上的B、C两点,OB=6,D为抛物线的顶点.M是线段BC上的一动点(M与B、C不重合),过M作MN⊥x轴,交抛物线于点N.
(1)k=
;b=
.
(2)求MN的最大值.
(3)如图②,若M是线段BC的中点,P是抛物线上的一动点,且点P在直线MN的右侧,连接PM、PC,当△PCM的面积是时,求此时点P的坐标.
参考答案
1.解:设正方形的边长为m,则m>0,
∵AE=x,
∴DH=x,
∴AH=m﹣x,
∵EH2=AE2+AH2,
∴y=x2+(m﹣x)2,
y=x2+x2﹣2mx+m2,
y=2x2﹣2mx+m2,
=2[(x﹣m)2+],
=2(x﹣m)2+m2,
∴y与x的函数图象是A.
故选:A.
2.解:依题意,设A点坐标为(﹣8,y),
代入抛物线方程得:y=﹣×64=﹣16,
即水面到桥拱顶点O的距离为16米.
故选:C.
3.解:如右图建立平面直角坐标系,
设抛物线的解析式为y=ax2,
由已知可得,点(2,﹣2)在此抛物线上,
则﹣2=a×22,
解得a=﹣,
∴y=﹣x2,
当y=﹣0.5时,﹣x2=﹣0.5,
解得x=±1,
此时水面的宽度为2m,
故选:B.
4.解:根据题意:
GH所在直线为x轴,GH的垂直平分线所在直线为y轴建立如图所示的平面直角坐标系,
喷口B为抛物线顶点,共线的三点B、D、H所在直线为抛物线的对称轴,
根据题意,Q(9,15.5),B(6,16),OH=6,
设抛物线解析式为
y=ax2+bx+c,
∵a=﹣,
将Q点和B点坐标代入,
得系数b=,c=14,
所以抛物线解析式为:
y=﹣x2+x+14.
符号题意:洗手液从喷口B流出,路线近似呈抛物线状,
当y=0时,即0=﹣x2+x+14,
解得:x=6+12(负值舍去),
所以洗手液落在台面的位置距DH的水平距离是12cm.
故选:B.
5.解:根据题意知,点B的横坐标的最大值为3,
即可知当对称轴过N点时,点B的横坐标最大,
此时的A点坐标为(﹣1,0),
当可知当对称轴过M点时,点A的横坐标最小,此时的B点坐标为(1,0),
此时A点的坐标最小为(﹣3,0),
故点A的横坐标的最小值为﹣3,
故选:A.
6.解:设二次函数的解析式为y=ax2+bx+c,
根据表可得:,
解得:,
∴y=﹣0.2x2+x+2.25=﹣0.2(x﹣2.5)2+3.5,
∴可推断出篮球飞行到最高点时,水平距离为2.5米,
故选:C.
7.解:2.5秒时,后球的高度为:
h2=﹣(2.5﹣3)2+40=,
则此时,前球的高度为h1=﹣=,
令﹣(t﹣3)2+40=,整理得(t﹣3)2=1,
∴t1=4,t2=2(舍),
△t=4﹣2.5=1.5.
故选:B.
8.解:当x=﹣1时,y1=x2﹣2x+k=1+2+k=k+3;
当x=时,y2=x2﹣2x+k=﹣1+k=k﹣,
所以y1>y2.
故选:A.
9.解:将图象中的三个点(3,0.8)、(4,0.9)、(5,0.6)代入函数关系P=at2+bt+c中,
,
解得,
所以函数关系式为:P=﹣0.2t2+1.5t﹣1.9,
由题意可知:加工煎炸臭豆腐的最佳时间为抛物线顶点的横坐标:
t=﹣=﹣=3.75,
则当t=3.75分钟时,可以得到最佳时间.
故选:C.
10.解:设y=kx+b,由图象可知,,
解之,得:,
∴y=﹣2x+60;
设销售利润为p,根据题意得,p=(x﹣10)y
=(x﹣10)(﹣2x+60)
=﹣2x2+80x﹣600,
∵a=﹣2<0,
∴p有最大值,
当x=﹣=20时,p最大值=200.
即当销售单价为20元/千克时,每天可获得最大利润200元,
故选:D.
11.解:由题意可得,抛物线经过点(0,1.5)和(3,0),
把上述两个点坐标代入二次函数表达式得:
,
解得:,
∴函数表达式为:y=﹣x2+x+,
=﹣(x﹣1)2+2,
∵a<0,故函数有最大值,
∴当x=1时,y取得最大值,此时y=2,
答:水流喷出的最大高度为2米.
故选:C.
12.解:①∵二次函数与x轴交于点A(﹣1,0)、B(3,0).
∴二次函数的对称轴为直线x==1,即﹣=1,
∴2a+b=0.
故①正确;
②∵二次函数y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0).
∴a﹣b+c=0,9a+3b+c=0.
又∵b=﹣2a.
∴3b=﹣6a,a﹣(﹣2a)+c=0.
∴3b=﹣6a,2c=﹣6a.
∴2c=3b.
故②错误;
③∵抛物线开口向上,对称轴是直线x=1.
∴x=1时,二次函数有最小值.
∴m≠1时,a+b+c<am2+bm+c.
即a+b<am2+bm.
故③正确;
④∵AD=BD,AB=4,△ABD是等腰直角三角形.
∴AD2+BD2=42.
解得,AD2=8.
设点D坐标为(1,y).
则[1﹣(﹣1)]2+y2=AD2.
解得y=±2.
∵点D在x轴下方.
∴点D为(1,﹣2).
∵二次函数的顶点D为(1,﹣2),过点A(﹣1,0).
设二次函数解析式为y=a(x﹣1)2﹣2.
∴0=a(﹣1﹣1)2﹣2.
解得a=.
故④正确;
⑤由图象可得,AC≠BC.
故△ABC是等腰三角形时,a的值有2个.(故⑤错误)
故①③④正确,②⑤错误.
故选:C.
13.解:由题意可得,
s=x(30﹣2x)=﹣2x2+30x,
故答案为:s=﹣2x2+30x
14.解:依题意,令h=0得0=35t﹣5t2,
得t(35﹣5t)=0,
解得t=0(舍去)或t=7,
即小球从飞出到落地所用的时间为7s.
故答案为7.
15.解:如图,以线段AC的中垂线为y轴,AB为x轴,建立平面直角坐标系,
则抛物线AC的顶点坐标为(0,16),
所以抛物线解析式为y=﹣x2+16,
当y=0时,x1=16,x2=﹣16,
∴点A的坐标为(﹣16,0),点C的坐标为(16,0),
∴AC=16﹣(﹣16)=16+16=32,
∴AB=3AC=96,
即桥长AB为96米;
故答案为:96.
16.解:建立如图所示的平面直角坐标系,
由题意可得:D点坐标为:(0,6),
∵AB=4,
∴B点的横坐标为:2,
故x=2时,y=2×4+6=14,
即B(2,14),
则DC=14﹣6=8,
故CE=DC+DE=8+2=10,
故答案为:10.
17.解:由题意可得,
y=100(1+x)2,
故答案为:y=100(1+x)2.
18.解:设日销售量y与上市时间t之间的函数关系式为y=kt,
30k=60,得k=2,
即日销售量y与上市时间t之间的函数关系式为y=2t,
当0<t≤20时,设单件的利润w与t之间的函数关系式为w=at,
20a=30,得a=1.5,
即当0<t≤20时,单件的利润w与t之间的函数关系式为w=1.5t,
当20<t≤30时,单件的利润w与t之间的函数关系式为w=30,
设日销售利润为W元,
当0<t≤20时,W=1.5t×2t=3t2,
故当t=20时,W取得最大值,此时W=1200,
当20<t≤30时,W=30×2t=60t,
故当t=30时,W取得最大值,此时W=1800,
综上所述,最大日销售利润为1800元,
故答案为:1800.
19.解:设获得的利润为y元,由题意得:
y=(x﹣100)(200﹣x)
=﹣x2+300x﹣20000
=﹣(x﹣150)2+2500
∵a=﹣1<0
∴当x=150元时,y取得最大值2500元,
故答案为150.
20.解:(1)根据题意得,w=(x﹣20)(﹣2x+80)=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∴当x=30时,每天的利润最大,最大利润为200元;
(2)令﹣2(x﹣30)2+200=150,
解得:x=35或x=25,
∵这种产品的销售价不高于每千克28元,
∴x=25,
答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元.
21.解:(1)由题意可得,y=20+×6=20+2x,
∴y与x之间的函数表达式是y=2x+20;
(2)由题意得,w=(50﹣30﹣x)(20+2x)=(20﹣x)(20+2x)=﹣2(x﹣5)2+450,
当x=5时,w有最大值450,
∴当售价为45元,利润最大为450元,
即当每台降低5元时获得最大利润,最大利润是450元.
22.解:(1)如图1,过点B作BD⊥x轴,垂足为D,
∵∠BCD+∠ACO=90°,∠AC0+∠OAC=90°,
∴∠BCD=∠CAO,
又∵∠BDC=∠COA=90°,CB=AC,
在△BDC和△COA中,
,
∴△BDC≌△COA(AAS),
∴BD=OC=1,CD=OA=2,
∴点B的坐标为(3,1),
故答案为(3,1);
(2)∵抛物线y=ax2﹣ax﹣2过点B(3,1),
∴1=9a﹣3a﹣2,
解得:a=,
∴抛物线的解析式为y=x2﹣x﹣2;
(3)A1在抛物线l上,理由:
旋转后如图2所示,过点A1作A1M⊥x轴,
∵把△ABC绕着点C逆时针旋转90°,
∴∠ABC=∠A1BC=90°,
∴A1,B,C共线,
在三角形BDC和三角形A1CM中,
,
∴△BDC≌△A1CM(AAS),
∴CM=CD=3﹣1=2,A1M=BD=1,
∴OM=1,
∴点A1(﹣1,﹣1),
把点x=﹣1代入y=x2﹣x﹣2,
y=﹣1,
∴点A1在抛物线上.
23.解:(1)Rt△ABC绕点O顺时针旋转90°得到Rt△COD,
则OD=OB=1,OC=OA=3,
故点A、B、C、D的坐标分别为(0,3)、(﹣1,0)、(3,0)、(0,1),
将点A、B的坐标代入抛物线表达式得,解得,
故抛物线的表达式为y=﹣x2+2x+3,
抛物线的对称轴为x=1,则点P(1,4);
(2)由,解得,
故点M、N的坐标分别为(,)、(2,3);
由y=﹣x+4知,当x=1时,y=,
设直线y=﹣x+4与对称轴x=1交于点F,则点F(1,),
S△PMN=S△PFM+S△PFN=×PF×(xN﹣xM)=×(4﹣)×(2﹣)=;
(3)存在,理由:
设点Q的坐标为(1,t),
则CD2=10,CQ2=22+t2,DQ2=12+(t﹣1)2,
当∠DQC为直角时,则10=22+t2+12+(t﹣1)2,解得t=﹣1或2;
当∠QDC为直角时,同理可得:t=4;
当∠DCQ为直角时,同理可得:t=﹣6,
故点Q的坐标为(1,﹣1)或(1,2)或(1,4)或(1,﹣6).
24.解:(1)由解析式可知,点A的坐标为(0,4),
∵S△OAB=×BO×4=6,
BO=3.所以B(3,0)或(﹣3,0),
∵二次函数与x轴的负半轴交于点B,
∴点B的坐标为(﹣3,0);
(2)把点B的坐标(﹣3,0)代入y=﹣x2+(k﹣1)x+4,
得﹣(﹣3)2+(k﹣1)×(﹣3)+4=0.
解得k﹣1=﹣,
∴所求二次函数的解析式为y=﹣x2﹣x+4;
(3)(Ⅰ)当点P在x轴上时,
①如图1,当AB=AP时,
则点P和点B关于y轴对称,
则点P的坐标为(3,0);
②如图2,当AB=BP时,
当点P在y轴左侧时,BP=AB=5,则OP=PB+OB=5+3=8,故点P(﹣8,0),
当点P在y轴右侧时,则BP′=5,过点P′(2,0),
点P的坐标为(2,0)或(﹣8,0);
③如图3,当AP=BP时,
设点P的坐标为(x,0),
根据题意,得=|x+3|.
解得x=.
∴点P的坐标为(,0);
故点P的坐标为(3,0),(2,0),(﹣8,0),(,0).
(Ⅱ)当点P在y轴上时,
同理可得,点P的坐标为(0,)或(0,9)或(0,﹣1)或(0,﹣4);
综上所述,点P的坐标为(3,0),(2,0),(﹣8,0),(,0)或(0,)或(0,9)或(0,﹣1)或(0,﹣4).
25.解:(1)∵OB=6,则点B(6,0),
将点B的坐标代入y=kx+2得,0=6k+2,解得k=﹣,
故一次函数表达式为y=﹣x+2,
令x=0,则y=2,故点C(0,2),则c=2,
故抛物线的表达式为y=x2+bx+2,
将点B的坐标代入上式并解得b=﹣,
故抛物线的表达式为y=x2﹣x+2,
故答案为﹣,﹣;
(2)设点N(x,x2﹣x+2),则点M(x,﹣x+2),
则MN=(﹣x+2)﹣(x2﹣x+2)=﹣x2+2x,
∵﹣<0,故MN有最大值,
当x=3时,MM的最大值为3;
(3)设点P(m,m2﹣m+2),
而点C(0,2),设直线CP交MN于点H,
由点PC的坐标得,直线PC的表达式为y=(m﹣7)x+2,
当x=3时,y=(m﹣7)x+2=m﹣5,即点H(3,m﹣5),
△PCM的面积=S△HMC+S△HMP=×MH×xP=×(m﹣5﹣1)×m=,
解得m=9或﹣3
∵点P在MN的右侧,故m>3,故舍去﹣3,
故点P的坐标为(9,8).
同课章节目录
