2021-2022学年人教版九年级数学上册24.1.1圆 同步练习题(word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.1.1圆 同步练习题(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 124.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 14:10:10 | ||
图片预览


文档简介
24.1.1圆
同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.下列条件中,能确定唯一一个圆的是(
)
A.以点O为圆心
B.以2
cm长为半径
C.以点O为圆心,5
cm长为半径
D.半径为2
cm,且经过点A
2.到点O的距离等于8
cm的点的集合是以点O为圆心,以8cm长为半径的圆.
3.如图,点O为⊙O的圆心,则线段_____________是⊙O的半径,线段_____________是⊙O的弦,其中最长的弦是_____________,_____________,_____________是劣弧.
4.过圆内一点(非圆心)有_____________条弦,有_____________条直径.
5.已知⊙O中,最长的弦长为16
cm,则⊙O的半径是(
)
A.4
cm
B.8
cm
C.16
cm
D.32
cm
6.已知AB是半径为5的圆的一条弦,则AB的长不可能是(
)
A.4
B.8
C.10
D.12
7.下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.其中正确的说法有(
)
A.1个
B.2个
C.3个
D.4个
8.如图,以坐标原点O为圆心的圆与y轴交于点A,B,且OA=1,则点B的坐标是(
)
A.(0,1)
B.(0,-1)
C.(1,0)
D.(-1,0)
9.如图,MN为⊙O的弦,∠MON=76°,则∠OMN的度数为(
)
A.38°
B.52°
C.76°
D.104°
10.如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
02中档题
11.如图,OA是⊙O的半径,B为OA上一点(且不与点O,A重合),过点B作OA的垂线交⊙O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为(
)
A.8
B.6
C.4
D.2
12.如图,AB为半圆O的直径,OC⊥AB交半圆于点C,点D是半圆上的动点(不与点A,B,C重合),点D从点A出发向点B运动.过点D作DE⊥AB,DF⊥OC,垂足分别为E,F,分别取DE和DF的中点M,N,连接MN.若AB=10,则下列关于MN的说法正确的是(
)
A.先变大后变小
B.先变小后变大
C.等于5
D.等于2.5
13.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的⊙O经过点B,则⊙O的半径为_____________.
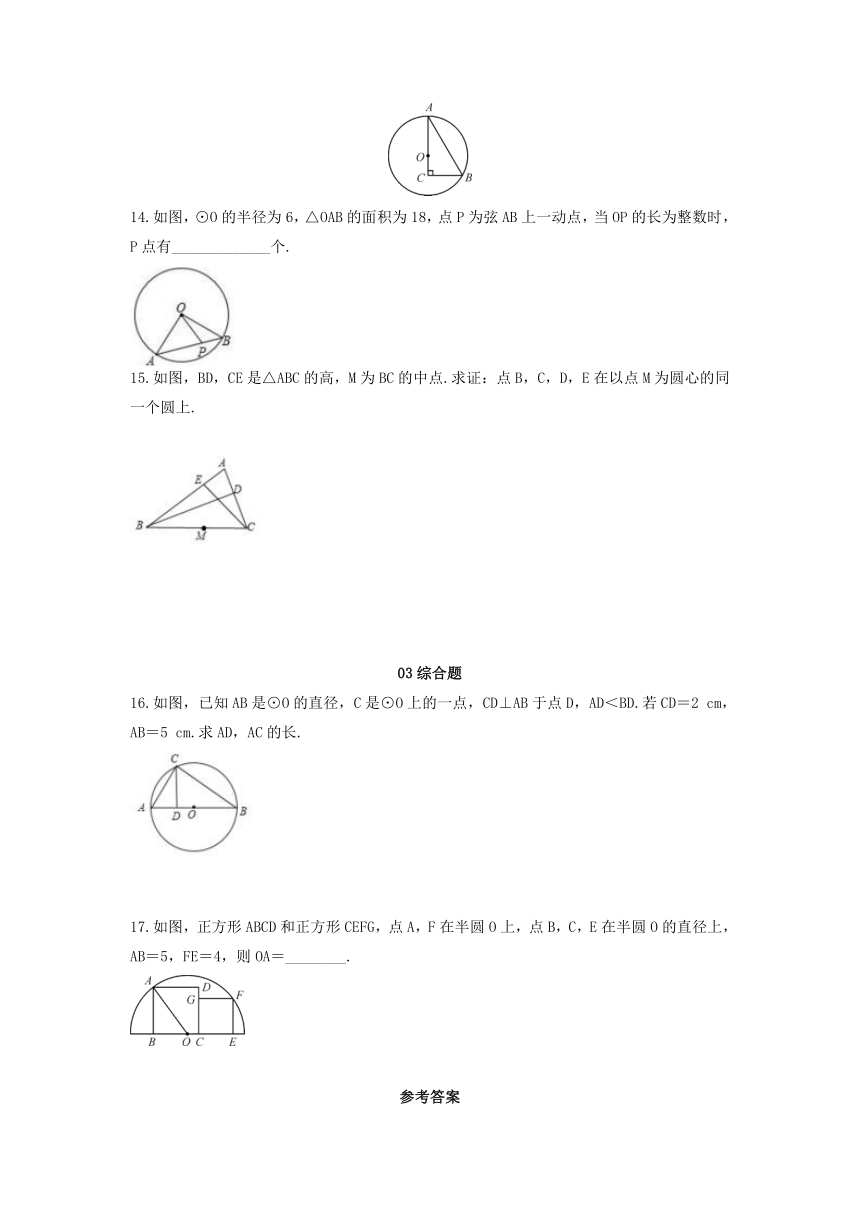
14.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP的长为整数时,P点有_____________个.
15.如图,BD,CE是△ABC的高,M为BC的中点.求证:点B,C,D,E在以点M为圆心的同一个圆上.
03综合题
16.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于点D,AD<BD.若CD=2
cm,AB=5
cm.求AD,AC的长.
17.如图,正方形ABCD和正方形CEFG,点A,F在半圆O上,点B,C,E在半圆O的直径上,AB=5,FE=4,则OA=________.
参考答案
24.1.1圆
同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.下列条件中,能确定唯一一个圆的是(C)
A.以点O为圆心
B.以2
cm长为半径
C.以点O为圆心,5
cm长为半径
D.半径为2
cm,且经过点A
2.到点O的距离等于8
cm的点的集合是以点O为圆心,以8cm长为半径的圆.
3.如图,点O为⊙O的圆心,则线段OA,OB,OC是⊙O的半径,线段AB,BC,AC是⊙O的弦,其中最长的弦是AC,,是劣弧.
4.过圆内一点(非圆心)有无数条弦,有1条直径.
5.已知⊙O中,最长的弦长为16
cm,则⊙O的半径是(B)
A.4
cm
B.8
cm
C.16
cm
D.32
cm
6.已知AB是半径为5的圆的一条弦,则AB的长不可能是(D)
A.4
B.8
C.10
D.12
7.下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.其中正确的说法有(C)
A.1个
B.2个
C.3个
D.4个
8.如图,以坐标原点O为圆心的圆与y轴交于点A,B,且OA=1,则点B的坐标是(B)
A.(0,1)
B.(0,-1)
C.(1,0)
D.(-1,0)
9.如图,MN为⊙O的弦,∠MON=76°,则∠OMN的度数为(B)
A.38°
B.52°
C.76°
D.104°
10.如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
证明:∵OB,OC是⊙O的半径,
∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC(ASA).
∴OE=OF.
∴OE+OC=OF+OB,即CE=BF.
02中档题
11.如图,OA是⊙O的半径,B为OA上一点(且不与点O,A重合),过点B作OA的垂线交⊙O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为(C)
A.8
B.6
C.4
D.2
12.如图,AB为半圆O的直径,OC⊥AB交半圆于点C,点D是半圆上的动点(不与点A,B,C重合),点D从点A出发向点B运动.过点D作DE⊥AB,DF⊥OC,垂足分别为E,F,分别取DE和DF的中点M,N,连接MN.若AB=10,则下列关于MN的说法正确的是(D)
A.先变大后变小
B.先变小后变大
C.等于5
D.等于2.5
13.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的⊙O经过点B,则⊙O的半径为.
14.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP的长为整数时,P点有4个.
解析:设△AOB中OA边上的高为h,过点O作OC⊥AB于点C.
则×OA·h=18,即×6h=18,
∴h=6.
∵OB=6,
∴OA⊥OB,即∠AOB=90°.
∴AB=6,图中OC=3.
同理得:点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
故答案为:4.
15.如图,BD,CE是△ABC的高,M为BC的中点.求证:点B,C,D,E在以点M为圆心的同一个圆上.
证明:连接ME,MD.
∵BD,CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC.
∴点B,C,D,E在以点M为圆心的同一个圆上.
03综合题
16.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于点D,AD<BD.若CD=2
cm,AB=5
cm.求AD,AC的长.
解:连接OC,
∵AB=5
cm,
∴OC=OA=AB=
cm.
在Rt△CDO中,由勾股定理,得
DO===(cm).
∴AD=-=1(cm).
在Rt△ACD中,由勾股定理,得
AC===(cm),
∴AD的长为1
cm,AC的长为
cm.
17.如图,正方形ABCD和正方形CEFG,点A,F在半圆O上,点B,C,E在半圆O的直径上,AB=5,FE=4,则OA=.
同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.下列条件中,能确定唯一一个圆的是(
)
A.以点O为圆心
B.以2
cm长为半径
C.以点O为圆心,5
cm长为半径
D.半径为2
cm,且经过点A
2.到点O的距离等于8
cm的点的集合是以点O为圆心,以8cm长为半径的圆.
3.如图,点O为⊙O的圆心,则线段_____________是⊙O的半径,线段_____________是⊙O的弦,其中最长的弦是_____________,_____________,_____________是劣弧.
4.过圆内一点(非圆心)有_____________条弦,有_____________条直径.
5.已知⊙O中,最长的弦长为16
cm,则⊙O的半径是(
)
A.4
cm
B.8
cm
C.16
cm
D.32
cm
6.已知AB是半径为5的圆的一条弦,则AB的长不可能是(
)
A.4
B.8
C.10
D.12
7.下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.其中正确的说法有(
)
A.1个
B.2个
C.3个
D.4个
8.如图,以坐标原点O为圆心的圆与y轴交于点A,B,且OA=1,则点B的坐标是(
)
A.(0,1)
B.(0,-1)
C.(1,0)
D.(-1,0)
9.如图,MN为⊙O的弦,∠MON=76°,则∠OMN的度数为(
)
A.38°
B.52°
C.76°
D.104°
10.如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
02中档题
11.如图,OA是⊙O的半径,B为OA上一点(且不与点O,A重合),过点B作OA的垂线交⊙O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为(
)
A.8
B.6
C.4
D.2
12.如图,AB为半圆O的直径,OC⊥AB交半圆于点C,点D是半圆上的动点(不与点A,B,C重合),点D从点A出发向点B运动.过点D作DE⊥AB,DF⊥OC,垂足分别为E,F,分别取DE和DF的中点M,N,连接MN.若AB=10,则下列关于MN的说法正确的是(
)
A.先变大后变小
B.先变小后变大
C.等于5
D.等于2.5
13.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的⊙O经过点B,则⊙O的半径为_____________.
14.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP的长为整数时,P点有_____________个.
15.如图,BD,CE是△ABC的高,M为BC的中点.求证:点B,C,D,E在以点M为圆心的同一个圆上.
03综合题
16.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于点D,AD<BD.若CD=2
cm,AB=5
cm.求AD,AC的长.
17.如图,正方形ABCD和正方形CEFG,点A,F在半圆O上,点B,C,E在半圆O的直径上,AB=5,FE=4,则OA=________.
参考答案
24.1.1圆
同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.下列条件中,能确定唯一一个圆的是(C)
A.以点O为圆心
B.以2
cm长为半径
C.以点O为圆心,5
cm长为半径
D.半径为2
cm,且经过点A
2.到点O的距离等于8
cm的点的集合是以点O为圆心,以8cm长为半径的圆.
3.如图,点O为⊙O的圆心,则线段OA,OB,OC是⊙O的半径,线段AB,BC,AC是⊙O的弦,其中最长的弦是AC,,是劣弧.
4.过圆内一点(非圆心)有无数条弦,有1条直径.
5.已知⊙O中,最长的弦长为16
cm,则⊙O的半径是(B)
A.4
cm
B.8
cm
C.16
cm
D.32
cm
6.已知AB是半径为5的圆的一条弦,则AB的长不可能是(D)
A.4
B.8
C.10
D.12
7.下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.其中正确的说法有(C)
A.1个
B.2个
C.3个
D.4个
8.如图,以坐标原点O为圆心的圆与y轴交于点A,B,且OA=1,则点B的坐标是(B)
A.(0,1)
B.(0,-1)
C.(1,0)
D.(-1,0)
9.如图,MN为⊙O的弦,∠MON=76°,则∠OMN的度数为(B)
A.38°
B.52°
C.76°
D.104°
10.如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
证明:∵OB,OC是⊙O的半径,
∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC(ASA).
∴OE=OF.
∴OE+OC=OF+OB,即CE=BF.
02中档题
11.如图,OA是⊙O的半径,B为OA上一点(且不与点O,A重合),过点B作OA的垂线交⊙O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为(C)
A.8
B.6
C.4
D.2
12.如图,AB为半圆O的直径,OC⊥AB交半圆于点C,点D是半圆上的动点(不与点A,B,C重合),点D从点A出发向点B运动.过点D作DE⊥AB,DF⊥OC,垂足分别为E,F,分别取DE和DF的中点M,N,连接MN.若AB=10,则下列关于MN的说法正确的是(D)
A.先变大后变小
B.先变小后变大
C.等于5
D.等于2.5
13.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的⊙O经过点B,则⊙O的半径为.
14.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP的长为整数时,P点有4个.
解析:设△AOB中OA边上的高为h,过点O作OC⊥AB于点C.
则×OA·h=18,即×6h=18,
∴h=6.
∵OB=6,
∴OA⊥OB,即∠AOB=90°.
∴AB=6,图中OC=3.
同理得:点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
故答案为:4.
15.如图,BD,CE是△ABC的高,M为BC的中点.求证:点B,C,D,E在以点M为圆心的同一个圆上.
证明:连接ME,MD.
∵BD,CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC.
∴点B,C,D,E在以点M为圆心的同一个圆上.
03综合题
16.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于点D,AD<BD.若CD=2
cm,AB=5
cm.求AD,AC的长.
解:连接OC,
∵AB=5
cm,
∴OC=OA=AB=
cm.
在Rt△CDO中,由勾股定理,得
DO===(cm).
∴AD=-=1(cm).
在Rt△ACD中,由勾股定理,得
AC===(cm),
∴AD的长为1
cm,AC的长为
cm.
17.如图,正方形ABCD和正方形CEFG,点A,F在半圆O上,点B,C,E在半圆O的直径上,AB=5,FE=4,则OA=.
同课章节目录
