2021-2022学年八年级数学人教版上册13.3.1等腰三角形同步习题(word版、含解析)
文档属性
| 名称 | 2021-2022学年八年级数学人教版上册13.3.1等腰三角形同步习题(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 294.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 14:20:06 | ||
图片预览


文档简介
2021-2022学年八年级数学上册同步(人教版)
13.3.1等腰三角形
时间:60分钟,
一、单选题
1.若等腰三角形的两边长为3和7,则该等腰三角形的周长为(
)
A.10
B.17
C.13
D.13或17
2.如图,D在AC上,E在AB上,若AB=AC,BC=BD,AD=DE=BE,则∠A的度数为( )
A.60°
B.72°
C.45°
D.50°
3.如图,在中,,为边上的中线,,则的度数为(
).
A.55°
B.65°
C.75°
D.45°
4.如图,∠AOB=60°,OC平分∠AOB,P为射线OC上一点,如果射线OA上的点D,满足△OPD是等腰三角形,那么∠ODP的度数为( )
A.30°
B.120°
C.30°或120°
D.30°或75°或120°
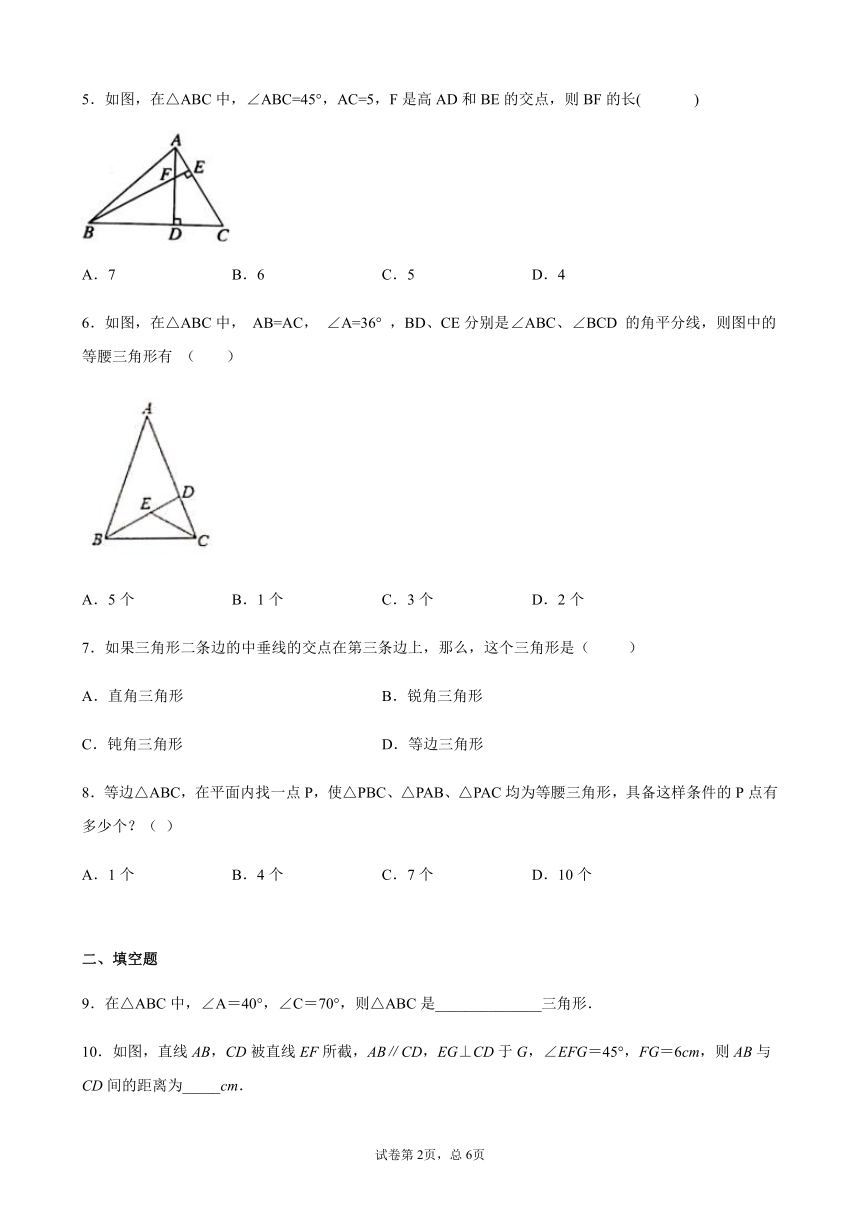
5.如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长(
)
A.7
B.6
C.5
D.4
6.如图,在△ABC中,
AB=AC,
∠A=36°
,BD、CE分别是∠ABC、∠BCD
的角平分线,则图中的等腰三角形有
(
)
A.5个
B.1个
C.3个
D.2个
7.如果三角形二条边的中垂线的交点在第三条边上,那么,这个三角形是(
)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
8.等边△ABC,在平面内找一点P,使△PBC、△PAB、△PAC均为等腰三角形,具备这样条件的P点有多少个?(
)
A.1个
B.4个
C.7个
D.10个
二、填空题
9.在△ABC中,∠A=40°,∠C=70°,则△ABC是______________三角形.
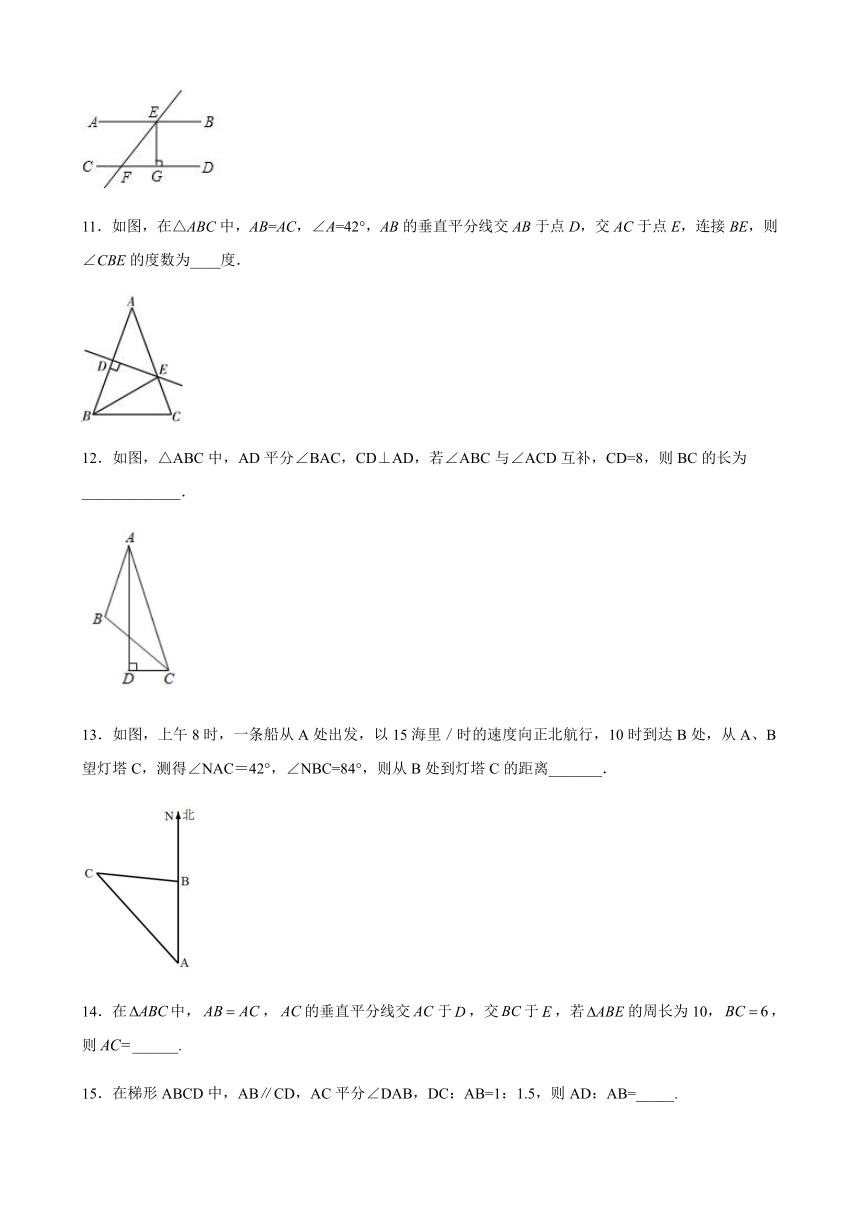
10.如图,直线AB,CD被直线EF所截,AB∥CD,EG⊥CD于G,∠EFG=45°,FG=6cm,则AB与CD间的距离为_____cm.
11.如图,在△ABC中,AB=AC,∠A=42°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为____度.
12.如图,△ABC中,AD平分∠BAC,CD⊥AD,若∠ABC与∠ACD互补,CD=8,则BC的长为_____________.
13.如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
14.在中,,的垂直平分线交于,交于,若的周长为10,,则______.
15.在梯形ABCD中,AB∥CD,AC平分∠DAB,DC:AB=1:1.5,则AD:AB=_____.
16.一个等腰三角形的周长是44厘米,三边长度之比是,这个等腰三角形的底边长是_______厘米.
三、解答题
17.如图,在中,,为的中点,,,垂足为、,
求证:.
18.如图,已知:在中,点D、E在BC上,且,求的周长.
19.已知:如图,AC=BD,1=2.求证:AD∥BC.
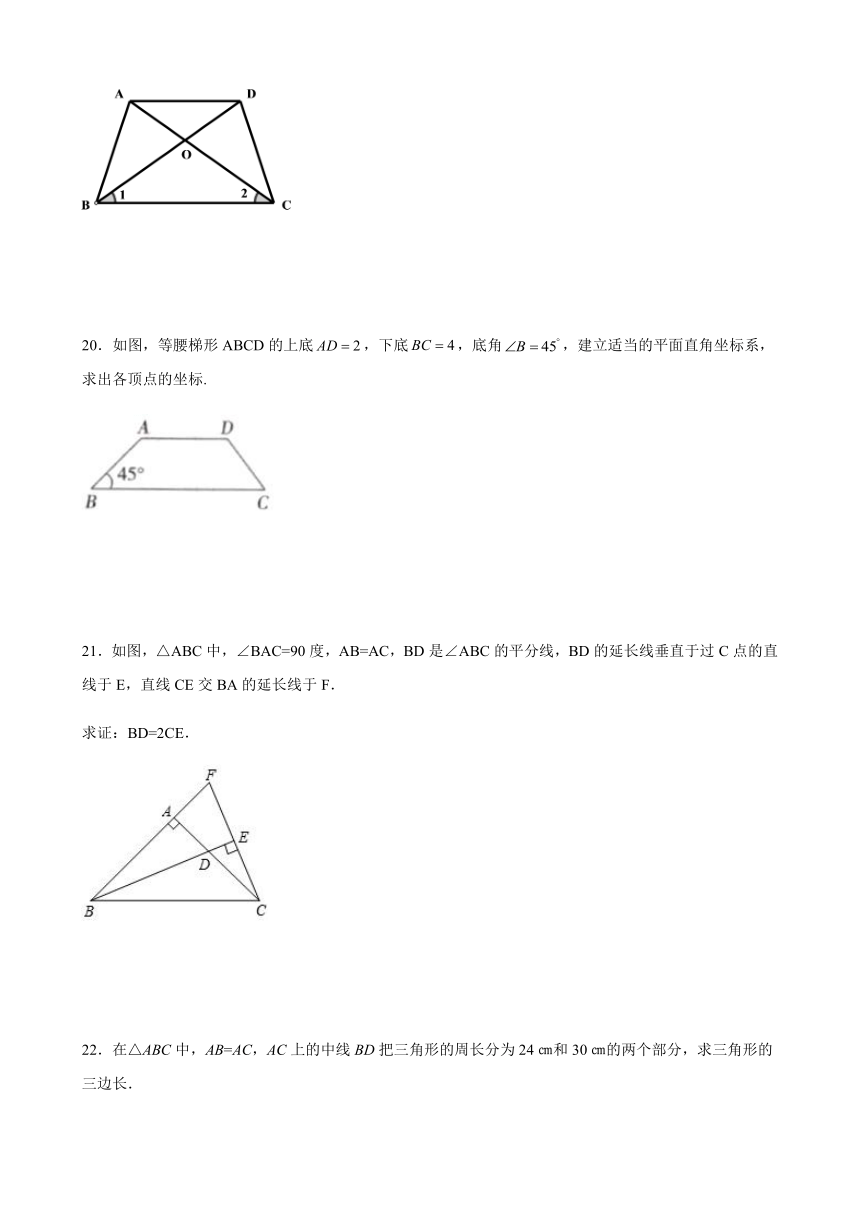
20.如图,等腰梯形ABCD的上底,下底,底角,建立适当的平面直角坐标系,求出各顶点的坐标.
21.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.
求证:BD=2CE.
22.在△ABC中,AB=AC,AC上的中线BD把三角形的周长分为24㎝和30㎝的两个部分,求三角形的三边长.
23.如图,直线l1,l2交于点B,A是直线l1上的点,在直线l2上寻找一点C,使△ABC是等腰三角形,请画出所有的等腰三角形.
24.等腰△ABC中,AB=AC,∠ACB=72°,
(1)如图1,若BD⊥AC于D,求∠ABD的度数;
(2)如图2,若CE平分∠ACB,求证:AE=BC.
试卷第1页,总3页
参考答案
1.B
【解析】解:当3为底时,其它两边都为7,3、7、7可以构成三角形,周长为17;
当3为腰时,其它两边为3和7,
∵3+3=6<7,
所以不能构成三角形,故舍去,
∴答案只有17.
故选:B.
2.C
【解析】解:∵AB=AC,
∴∠ABC=∠C,
又∵BC=BD,
∴∠BDC=∠C,
∵∠A+∠C+∠ABC=180°,∠DBC+∠C+∠BDC=180°,
∴∠DBC=∠A,
∵AD=DE=EB,
∴∠A=∠AED,∠EDB=∠EBD,
∴∠A=2∠DBE,即∠ABC=3∠DBE,
∵∠A+2∠C=180°,
∴2∠DBE+2∠ABC=180°,
∴2∠DBE+2×(3∠DBE)=180°,
即8∠DBE=180°,
∴∠A=2∠DBE=45°.
故选:C.
3.B
【解析】∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠B+∠BAD=90°,
∵∠B=25°,
∴∠BAD=65°,
故选:B.
4.D
【解析】解:∵∠AOB=60°,OC平分∠AOB,
∴∠AOC=30°,
①当D在D1时,OD=PD,
∵∠AOP=∠OPD=30°,
∴∠ODP=180°﹣30°﹣30°=120°;
②当D在D2点时,OP=OD,
则∠OPD=∠ODP=(180°﹣30°)=75°;
③当D在D3时,OP=DP,
则∠ODP=∠AOP=30°;
综上所述:120°或75°或30°,
故选:D.
5.C
【解析】∵AD、BE是高,
∴∠ADC=∠BDF=90°,∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
∵∠ABC=45°,∠ADB=90°,
∴∠BAD=∠ABD=45°,
∴AD=BD,
在△ADC和△BDF中
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AC=5,
∴BF=5,
故选C.
6.A
【解析】解:∵AB=AC,
∴△ABC是等腰三角形;
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∵BD、CE分别是∠ABC、∠BCD的角平分线,
∴∠ABD=∠DBC=∠ABC=36°,∠BCE=∠ACE=∠ACB=36°,
∴∠DBC=∠BCE,∠CED=∠DBC+∠BCE=36°+36°=72°,
∠A=∠ABD,∠BDC=180°﹣∠DBC﹣∠BCD=180°﹣72°﹣36°=72°,
∴△EBC、△ABD是等腰三角形;
∠BDC=∠BCD,∠CED=∠CDE,
∴△BCD、△CDE是等腰三角形,
∴图中的等腰三角形有5个.
故选:A.
7.A
【解析】如图,CA、CB的中点分别为D、E,CA、CB的垂直平分线OD、OE相交于点O,且点O落在AB边上,
连接CO,
∵OD是AC的垂直平分线,
∴OC=OA,∠A=∠ACO,
同理OC=OB,∠B=∠BCO,
∵∠A+∠ACO+∠B+∠BCO=180,
∴∠ACO
+∠BCO=180=90,
∴∠C是直角.
故选:A.
8.D
【解析】解:由点P在等边△ABC内,而且△PBC、△PAB、△PAC均为等腰三角形,
可知P点为等边△ABC的垂心;
因为△ABC是等边三角形,所以分别以三角形各顶点为圆心,边长为半径画弧,交垂直平分线的交点就是满足要求的,
每条垂直平分线上得3个交点,再加三角形的垂心,一共10个.
故选D.
9.等腰
【解析】解:∵在△ABC中,∠A=40°,∠C=70°,
∴∠B=180°-∠A-∠C=70°
∴∠B=∠C
∴△ABC为等腰三角形
故答案为:等腰.
10.6.
【解析】解:∵EG⊥CD,∴∠EGF=90°,
∵∠EFG=45°,∴∠FEG=45°,
∴∠EFG=∠FEG
,∴FG=EG,
∵FG=6cm,∴EG=6cm,
∴AB与CD间的距离为6cm.
故答案为6.
11.27
【解析】∵AB=AC,∠A=42°,
∴∠ABC=∠C=69°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=42°,
∴∠CBE=∠ABC-∠EBA=27°,
故答案为:27.
12.16
【解析】解:延长AB交CD的延长线于点E,如图所示:
∵AD平分∠BAC,CD⊥AD,
∴∠EAD=∠CAD,∠ADE=∠ADC=90°,
∵AD=AD,
∴△ADE≌△ADC,
∴∠E=∠ACD,ED=DC,
又∵∠ABC+∠ACD=180°,∠ABC+∠EBC=180°,
∴∠E=∠ACD=∠EBC,
∴BC=EC=2DC,
∵DC=8,
∴BC=EC=16;
故答案为16.
13.30海里
【解析】根据题意得:AB=2×15=30(海里),
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC?∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=30海里.
即从海岛B到灯塔C的距离是30海里.
故答案为30海里.
14.4
【解析】∵AC的垂直平分线交AC于D,交BC于E,
∴EA=EC,
∵△ABE的周长为10,BC=6,
∴AB+BE+AE=AB+BE+EC=AB+BC=10,
∴AB=AC=4,
故答案为4.
15.1:1.5
【解析】解:∵AB∥CD
∴∠DCA=∠CAB
∵AC平分∠DAB
∴∠CAB=∠CAD
=∠DCA
∴AD
=
CD
∵DC∶AB=1∶1.5
∴AD∶AB=1∶1.5
16.20
【解析】由题意,设这个等腰三角形的三边长度分别为厘米、厘米、厘米,
则,
解得,
则这个等腰三角形的底边长是(厘米),
故答案为:20.
17.见解析
【解析】解:,
,
,,
,
为的中点,
,
在与中
,
≌,
∴.
18.10cm.
【解析】∵∠1=∠B,∠2=∠C,
∴BD=AD,AE=CE,
∵△ADE的周长=AD+DE+AE,
∴△ADE的周长=BD+DE+CE=BC=10cm.
19.见解析
【解析】证明:
因为1=2.
所以OB=OC.
因为AC=BD.
所以OA=OD.
所以∠OAD=∠ODA.
因为1+2+∠BOC=180°.
∠OAD+∠ODA+∠AOD=180°.
∠BOC=∠AOD.
所以1+2=∠OAD+∠ODA.
所以21=2∠ODA.
即1=∠ODA.
所以AD∥BC.
20.见解析,A(0,1),B(?1,0),C(3,0),D(2,1).
【解析】作AE⊥BC,DF⊥BC分别与E,F,则EF=AD=2,BE=CF=1,
直角△ABE中,∠B=45°,则其为等腰直角三角形,因而AE=BE=1,CE=3.
以BC所在的直线为x轴,由B向C的方向为正方向,AE所在的直线为y轴,由E向A的方向为正方向建立坐标系,
则A(0,1),B(?1,0),C(3,0),D(2,1).
21.见解析
【解析】∵BE平分∠FBC,BE⊥CF,
∴BF=BC,CE=EF,
∴CF=2CE,
∵∠BAC=90°,且AB=AC,
∴∠FAC=∠BAC=90°,∠ABC=∠ACB=45°,
∴∠FBE=∠CBE=22.5°,
∴∠F=∠ADB=67.5°,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(AAS),
∴BD=CF,
∴BD=2CE.
22.16cm,16
cm,22
cm或20
cm,20
cm,14
cm.
【解析】解:如图所示
设三角形的腰AB=AC=x
cm,分两种情况讨论:
(1)若AB+AD=24cm,则
x+
x=24
∴x=16
∵三角形的周长为24+30=54cm
所以三边长分别为16cm,16
cm,22
cm
(2)若AB+AD=30cm
,则
x+
x=30
∴x=20
∵三角形的周长为24+30=54cm
∴三边长分别为20
cm,20
cm,14
cm
因此,三角形的三边长为16
cm,16
cm,22
cm或20
cm,20
cm,14
cm.
23.4个
【解析】具体作法如下,如图,
(1)当以线段AB为腰时,点A为顶点时,可以以点A为圆心,线段AB为半径画圆,圆与直线l2
的交点即为点C,此时有1个,
(2)当以线段AB为腰时,点B为顶点时,可以以点B为圆心,线段BA为半径画圆,圆与直线l2
的交点即为点C,此时有2个,
(3)当以线段AB为底边,可以作线段AB的垂直平分线,线段垂直平分线与直线l2
的交点即为点C,此时有1个.
故共有4个满足题意的等腰三角形.
24.(1)∠ABD=54°;(2)见解析
【解析】解:∵等腰中,,,
∴,.
(1)∵于D,∴,
∴;
(2)∵CE平分∠ACB,,
∴,
∴,
∴,
∵,
∴,
∴
,
∴,
∴.
答案第1页,总2页
答案第1页,总2页
13.3.1等腰三角形
时间:60分钟,
一、单选题
1.若等腰三角形的两边长为3和7,则该等腰三角形的周长为(
)
A.10
B.17
C.13
D.13或17
2.如图,D在AC上,E在AB上,若AB=AC,BC=BD,AD=DE=BE,则∠A的度数为( )
A.60°
B.72°
C.45°
D.50°
3.如图,在中,,为边上的中线,,则的度数为(
).
A.55°
B.65°
C.75°
D.45°
4.如图,∠AOB=60°,OC平分∠AOB,P为射线OC上一点,如果射线OA上的点D,满足△OPD是等腰三角形,那么∠ODP的度数为( )
A.30°
B.120°
C.30°或120°
D.30°或75°或120°
5.如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长(
)
A.7
B.6
C.5
D.4
6.如图,在△ABC中,
AB=AC,
∠A=36°
,BD、CE分别是∠ABC、∠BCD
的角平分线,则图中的等腰三角形有
(
)
A.5个
B.1个
C.3个
D.2个
7.如果三角形二条边的中垂线的交点在第三条边上,那么,这个三角形是(
)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
8.等边△ABC,在平面内找一点P,使△PBC、△PAB、△PAC均为等腰三角形,具备这样条件的P点有多少个?(
)
A.1个
B.4个
C.7个
D.10个
二、填空题
9.在△ABC中,∠A=40°,∠C=70°,则△ABC是______________三角形.
10.如图,直线AB,CD被直线EF所截,AB∥CD,EG⊥CD于G,∠EFG=45°,FG=6cm,则AB与CD间的距离为_____cm.
11.如图,在△ABC中,AB=AC,∠A=42°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为____度.
12.如图,△ABC中,AD平分∠BAC,CD⊥AD,若∠ABC与∠ACD互补,CD=8,则BC的长为_____________.
13.如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
14.在中,,的垂直平分线交于,交于,若的周长为10,,则______.
15.在梯形ABCD中,AB∥CD,AC平分∠DAB,DC:AB=1:1.5,则AD:AB=_____.
16.一个等腰三角形的周长是44厘米,三边长度之比是,这个等腰三角形的底边长是_______厘米.
三、解答题
17.如图,在中,,为的中点,,,垂足为、,
求证:.
18.如图,已知:在中,点D、E在BC上,且,求的周长.
19.已知:如图,AC=BD,1=2.求证:AD∥BC.
20.如图,等腰梯形ABCD的上底,下底,底角,建立适当的平面直角坐标系,求出各顶点的坐标.
21.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.
求证:BD=2CE.
22.在△ABC中,AB=AC,AC上的中线BD把三角形的周长分为24㎝和30㎝的两个部分,求三角形的三边长.
23.如图,直线l1,l2交于点B,A是直线l1上的点,在直线l2上寻找一点C,使△ABC是等腰三角形,请画出所有的等腰三角形.
24.等腰△ABC中,AB=AC,∠ACB=72°,
(1)如图1,若BD⊥AC于D,求∠ABD的度数;
(2)如图2,若CE平分∠ACB,求证:AE=BC.
试卷第1页,总3页
参考答案
1.B
【解析】解:当3为底时,其它两边都为7,3、7、7可以构成三角形,周长为17;
当3为腰时,其它两边为3和7,
∵3+3=6<7,
所以不能构成三角形,故舍去,
∴答案只有17.
故选:B.
2.C
【解析】解:∵AB=AC,
∴∠ABC=∠C,
又∵BC=BD,
∴∠BDC=∠C,
∵∠A+∠C+∠ABC=180°,∠DBC+∠C+∠BDC=180°,
∴∠DBC=∠A,
∵AD=DE=EB,
∴∠A=∠AED,∠EDB=∠EBD,
∴∠A=2∠DBE,即∠ABC=3∠DBE,
∵∠A+2∠C=180°,
∴2∠DBE+2∠ABC=180°,
∴2∠DBE+2×(3∠DBE)=180°,
即8∠DBE=180°,
∴∠A=2∠DBE=45°.
故选:C.
3.B
【解析】∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠B+∠BAD=90°,
∵∠B=25°,
∴∠BAD=65°,
故选:B.
4.D
【解析】解:∵∠AOB=60°,OC平分∠AOB,
∴∠AOC=30°,
①当D在D1时,OD=PD,
∵∠AOP=∠OPD=30°,
∴∠ODP=180°﹣30°﹣30°=120°;
②当D在D2点时,OP=OD,
则∠OPD=∠ODP=(180°﹣30°)=75°;
③当D在D3时,OP=DP,
则∠ODP=∠AOP=30°;
综上所述:120°或75°或30°,
故选:D.
5.C
【解析】∵AD、BE是高,
∴∠ADC=∠BDF=90°,∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
∵∠ABC=45°,∠ADB=90°,
∴∠BAD=∠ABD=45°,
∴AD=BD,
在△ADC和△BDF中
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AC=5,
∴BF=5,
故选C.
6.A
【解析】解:∵AB=AC,
∴△ABC是等腰三角形;
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∵BD、CE分别是∠ABC、∠BCD的角平分线,
∴∠ABD=∠DBC=∠ABC=36°,∠BCE=∠ACE=∠ACB=36°,
∴∠DBC=∠BCE,∠CED=∠DBC+∠BCE=36°+36°=72°,
∠A=∠ABD,∠BDC=180°﹣∠DBC﹣∠BCD=180°﹣72°﹣36°=72°,
∴△EBC、△ABD是等腰三角形;
∠BDC=∠BCD,∠CED=∠CDE,
∴△BCD、△CDE是等腰三角形,
∴图中的等腰三角形有5个.
故选:A.
7.A
【解析】如图,CA、CB的中点分别为D、E,CA、CB的垂直平分线OD、OE相交于点O,且点O落在AB边上,
连接CO,
∵OD是AC的垂直平分线,
∴OC=OA,∠A=∠ACO,
同理OC=OB,∠B=∠BCO,
∵∠A+∠ACO+∠B+∠BCO=180,
∴∠ACO
+∠BCO=180=90,
∴∠C是直角.
故选:A.
8.D
【解析】解:由点P在等边△ABC内,而且△PBC、△PAB、△PAC均为等腰三角形,
可知P点为等边△ABC的垂心;
因为△ABC是等边三角形,所以分别以三角形各顶点为圆心,边长为半径画弧,交垂直平分线的交点就是满足要求的,
每条垂直平分线上得3个交点,再加三角形的垂心,一共10个.
故选D.
9.等腰
【解析】解:∵在△ABC中,∠A=40°,∠C=70°,
∴∠B=180°-∠A-∠C=70°
∴∠B=∠C
∴△ABC为等腰三角形
故答案为:等腰.
10.6.
【解析】解:∵EG⊥CD,∴∠EGF=90°,
∵∠EFG=45°,∴∠FEG=45°,
∴∠EFG=∠FEG
,∴FG=EG,
∵FG=6cm,∴EG=6cm,
∴AB与CD间的距离为6cm.
故答案为6.
11.27
【解析】∵AB=AC,∠A=42°,
∴∠ABC=∠C=69°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=42°,
∴∠CBE=∠ABC-∠EBA=27°,
故答案为:27.
12.16
【解析】解:延长AB交CD的延长线于点E,如图所示:
∵AD平分∠BAC,CD⊥AD,
∴∠EAD=∠CAD,∠ADE=∠ADC=90°,
∵AD=AD,
∴△ADE≌△ADC,
∴∠E=∠ACD,ED=DC,
又∵∠ABC+∠ACD=180°,∠ABC+∠EBC=180°,
∴∠E=∠ACD=∠EBC,
∴BC=EC=2DC,
∵DC=8,
∴BC=EC=16;
故答案为16.
13.30海里
【解析】根据题意得:AB=2×15=30(海里),
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC?∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=30海里.
即从海岛B到灯塔C的距离是30海里.
故答案为30海里.
14.4
【解析】∵AC的垂直平分线交AC于D,交BC于E,
∴EA=EC,
∵△ABE的周长为10,BC=6,
∴AB+BE+AE=AB+BE+EC=AB+BC=10,
∴AB=AC=4,
故答案为4.
15.1:1.5
【解析】解:∵AB∥CD
∴∠DCA=∠CAB
∵AC平分∠DAB
∴∠CAB=∠CAD
=∠DCA
∴AD
=
CD
∵DC∶AB=1∶1.5
∴AD∶AB=1∶1.5
16.20
【解析】由题意,设这个等腰三角形的三边长度分别为厘米、厘米、厘米,
则,
解得,
则这个等腰三角形的底边长是(厘米),
故答案为:20.
17.见解析
【解析】解:,
,
,,
,
为的中点,
,
在与中
,
≌,
∴.
18.10cm.
【解析】∵∠1=∠B,∠2=∠C,
∴BD=AD,AE=CE,
∵△ADE的周长=AD+DE+AE,
∴△ADE的周长=BD+DE+CE=BC=10cm.
19.见解析
【解析】证明:
因为1=2.
所以OB=OC.
因为AC=BD.
所以OA=OD.
所以∠OAD=∠ODA.
因为1+2+∠BOC=180°.
∠OAD+∠ODA+∠AOD=180°.
∠BOC=∠AOD.
所以1+2=∠OAD+∠ODA.
所以21=2∠ODA.
即1=∠ODA.
所以AD∥BC.
20.见解析,A(0,1),B(?1,0),C(3,0),D(2,1).
【解析】作AE⊥BC,DF⊥BC分别与E,F,则EF=AD=2,BE=CF=1,
直角△ABE中,∠B=45°,则其为等腰直角三角形,因而AE=BE=1,CE=3.
以BC所在的直线为x轴,由B向C的方向为正方向,AE所在的直线为y轴,由E向A的方向为正方向建立坐标系,
则A(0,1),B(?1,0),C(3,0),D(2,1).
21.见解析
【解析】∵BE平分∠FBC,BE⊥CF,
∴BF=BC,CE=EF,
∴CF=2CE,
∵∠BAC=90°,且AB=AC,
∴∠FAC=∠BAC=90°,∠ABC=∠ACB=45°,
∴∠FBE=∠CBE=22.5°,
∴∠F=∠ADB=67.5°,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(AAS),
∴BD=CF,
∴BD=2CE.
22.16cm,16
cm,22
cm或20
cm,20
cm,14
cm.
【解析】解:如图所示
设三角形的腰AB=AC=x
cm,分两种情况讨论:
(1)若AB+AD=24cm,则
x+
x=24
∴x=16
∵三角形的周长为24+30=54cm
所以三边长分别为16cm,16
cm,22
cm
(2)若AB+AD=30cm
,则
x+
x=30
∴x=20
∵三角形的周长为24+30=54cm
∴三边长分别为20
cm,20
cm,14
cm
因此,三角形的三边长为16
cm,16
cm,22
cm或20
cm,20
cm,14
cm.
23.4个
【解析】具体作法如下,如图,
(1)当以线段AB为腰时,点A为顶点时,可以以点A为圆心,线段AB为半径画圆,圆与直线l2
的交点即为点C,此时有1个,
(2)当以线段AB为腰时,点B为顶点时,可以以点B为圆心,线段BA为半径画圆,圆与直线l2
的交点即为点C,此时有2个,
(3)当以线段AB为底边,可以作线段AB的垂直平分线,线段垂直平分线与直线l2
的交点即为点C,此时有1个.
故共有4个满足题意的等腰三角形.
24.(1)∠ABD=54°;(2)见解析
【解析】解:∵等腰中,,,
∴,.
(1)∵于D,∴,
∴;
(2)∵CE平分∠ACB,,
∴,
∴,
∴,
∵,
∴,
∴
,
∴,
∴.
答案第1页,总2页
答案第1页,总2页
