2021秋季八年级上册十一章11.1.2- 三角形的高、中线和角平分线-同步课时训练(word版,含解析)
文档属性
| 名称 | 2021秋季八年级上册十一章11.1.2- 三角形的高、中线和角平分线-同步课时训练(word版,含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 425.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 10:31:50 | ||
图片预览



文档简介
2021秋季八年级上册十一章11.1.2-
三角形的高、中线和角平分线-同步课时训练学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图AD⊥BC于点D,那么图中以AD为高的三角形的个数有(
)
A.3
B.4
C.5
D.6
2.下面四个图形中,线段是的高的是(
)
A.
B.
C.
D.
3.钝角三角形三条高所在的直线交于( )
A.三角形内
B.三角形外
C.三角形的边上
D.不能确定
4.如图,已知于点,于点,于点,则中边上的高是(
)
A.
B.
C.
D.
5.下列说法正确的个数有(
)
①三角形的高、中线、角平分线都是线段;
②三角形的三条角平分线都在三角形内部,且交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
A.1个
B.2个
C.3个
D.4个
6.如图,D,E分别是的边AC,BC的中点,则下列说法错误的是(
)
A.DE是的中线
B.BD是的中线
C.
D.BD是的角平分线
7.如图,与交于点,点在上,根据尺规作图的痕迹,判断下列说法正确的是(
)
A.
B.点到三边的距离相等
C.
D.
8.如图,和是的中线,与交于点下列结论正确的有(
)个.
(1)
(2)
(3)S四边形DOEC
A.个
B.个
C.个
D.个
9.如图,△ABF的面积是2,D是AB边上任意一点,E是CD中点,F是BE中点,△ABC的面积是( )
A.4
B.6
C.8
D.16
10.如图,
∠1=∠2,∠3=∠4,下列结论错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
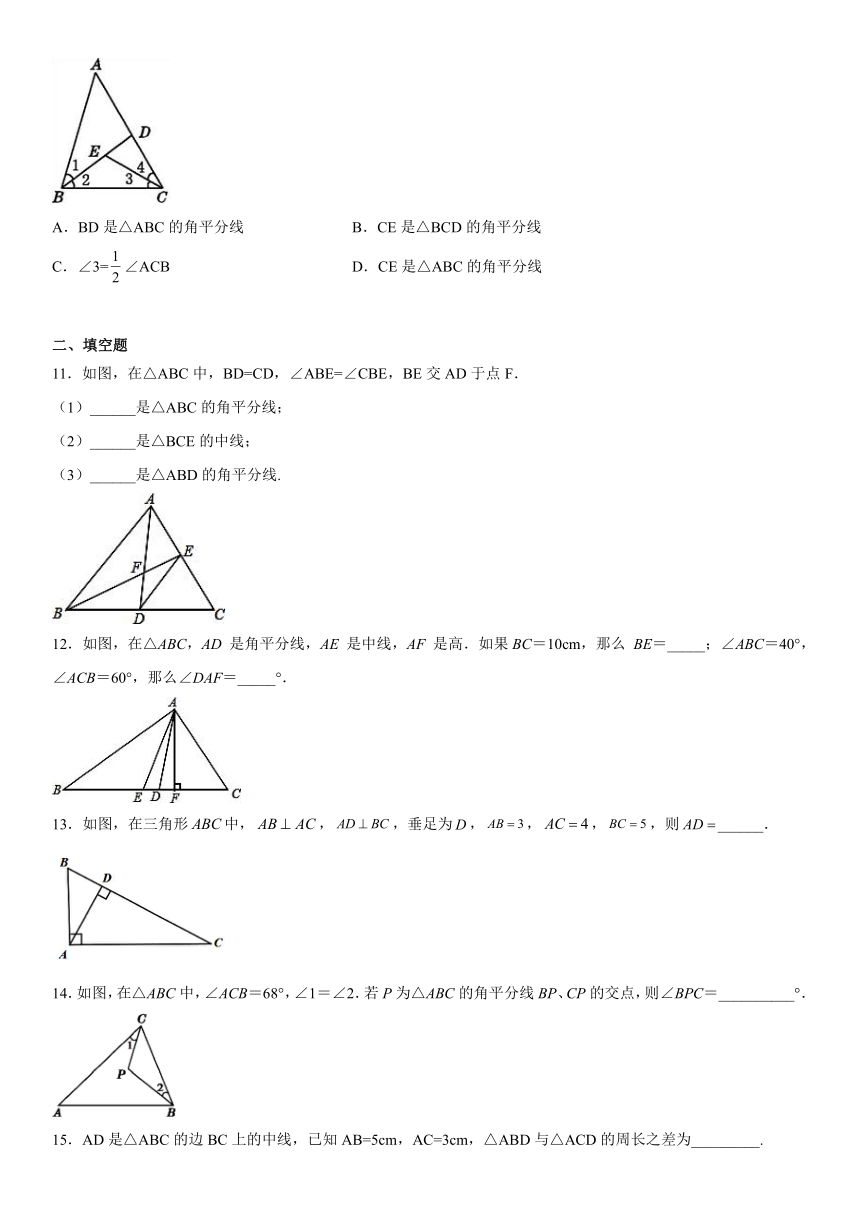
C.∠3=∠ACB
D.CE是△ABC的角平分线
二、填空题
11.如图,在△ABC中,BD=CD,∠ABE=∠CBE,BE交AD于点F.
(1)______是△ABC的角平分线;
(2)______是△BCE的中线;
(3)______是△ABD的角平分线.
12.如图,在△ABC,AD
是角平分线,AE
是中线,AF
是高.如果BC=10cm,那么
BE=_____;∠ABC=40°,∠ACB=60°,那么∠DAF=_____°.
13.如图,在三角形中,,,垂足为,,,,则______.
14.如图,在△ABC中,∠ACB=68°,∠1=∠2.若P为△ABC的角平分线BP、CP的交点,则∠BPC=__________°.
15.AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,△ABD与△ACD的周长之差为_________.
三、解答题
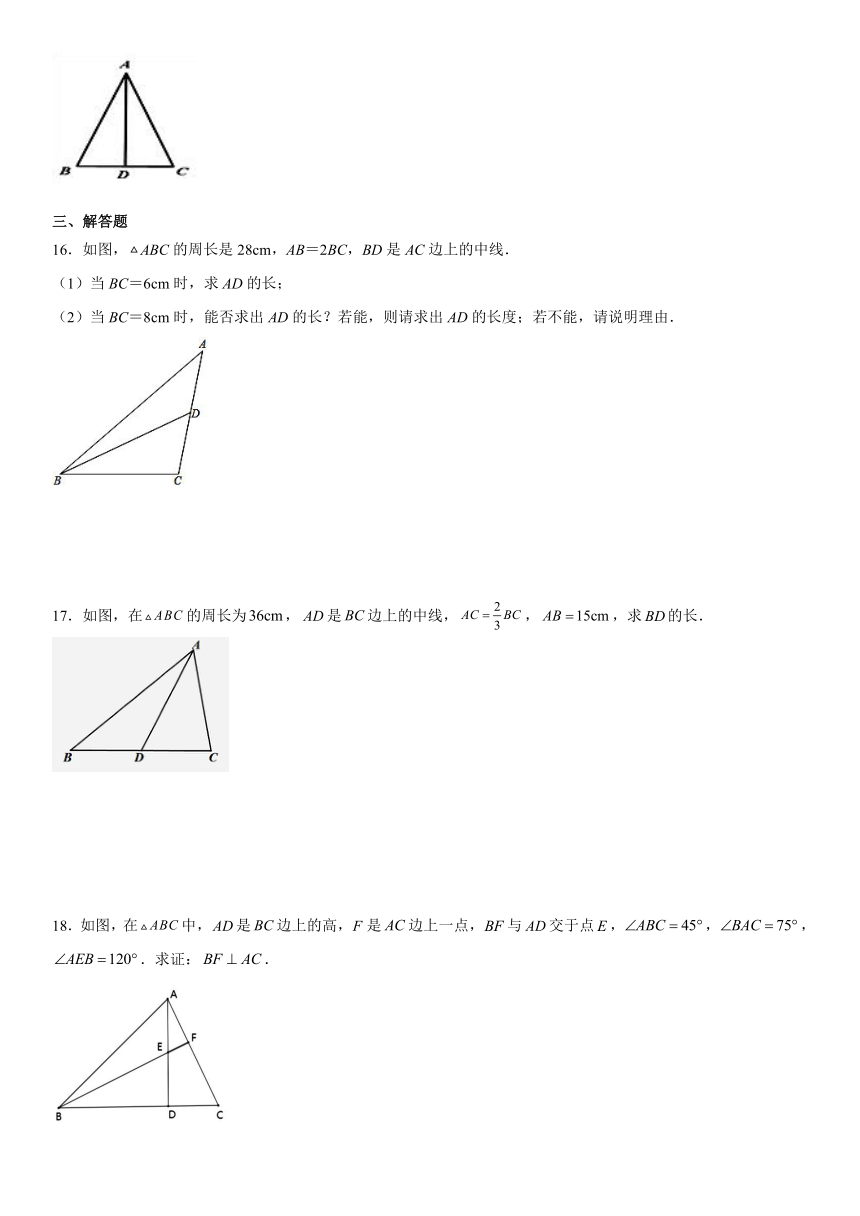
16.如图,ABC的周长是28cm,AB=2BC,BD是AC边上的中线.
(1)当BC=6cm时,求AD的长;
(2)当BC=8cm时,能否求出AD的长?若能,则请求出AD的长度;若不能,请说明理由.
17.如图,在的周长为,是边上的中线,,,求的长.
18.如图,在中,是边上的高,是边上一点,与交于点,,,.求证:.
19.如图,已知,分别是的高和中线,,,,.试求:
(1)的长;
(2)的面积;
(3)和的周长差.
参考答案
1.D
【详解】
结合三角形高的定义可知,以AD为高的三角形有:△ABD,△ABE,△ABC,△ADE,△ADC,△AEC,共6个.
故选D.
2.D
【分析】
根据三角形高的定义进行判断.
【详解】
解:线段AD是△ABC的高,则过点A作对边BC的垂线,则垂线段AD为△ABC的高.
选项A、B、C错误,
故选:D.
【点睛】
本题考查了三角形的高:三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.
3.B
【分析】
由图形可知:钝角三角形三条高所在的直线交于三角形外.
【详解】
解:如图可知:钝角△ABC三边的高交于三角形外部一点D,
即钝角三角形三条高所在的直线交于三角形外,
故选:B.
【点睛】
本题考查三角形的高线的交点问题,解答的关键是会画三角形的高线,并能根据三角形的形状得出三条高线所在的直线的交点与三角形的关系.
4.D
【分析】
从三角形的一个顶点向它的对边引垂线,顶点和垂足间的线段叫做三角形的高.根据此概念求解即可.
【详解】
A、CF⊥AB,∴线段CF是△ABC中AB边上的高,此选项不符合题意;
B、BE⊥AC,∴线段BE是△ABC中AC边上的高,此选项不符合题意;
C、CD不是△ABC的高,此选项不符合题意;
D、AD⊥BC,∴线段AD是△ABC中BC边上的高,此选项符合题意;
故选:D.
【点睛】
本题主要考查了三角形的高.准确识图并熟记三角形高的定义是解题的关键.
5.C
【分析】
根据三角形的三条中线都在三角形内部;三角形的三条角平分线都在三角形内部;三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上即可作答.
【详解】
解:①三角形的中线、角平分线、高都是线段,故正确;
②三角形的三条角平分线都在三角形内部,且交于同一点,故正确;
③钝角三角形的高有两条在三角形外部,故错误;
④三角形的一条中线把该三角形分成面积相等的两部分,故正确.
所以正确的有3个.
故选:C.
【点睛】
本题考查对三角形的中线、角平分线、高的正确理解,熟练掌握三角形的中线、角平分线、高的概念是解决本题的关键.
6.D
【分析】
根据三角形的中线、线段中点的定义、三角形的角平分线判断即可得.
【详解】
点D,E分别是的边AC,BC的中点,
,
是的边AC上的中线,DE是的边BC上的中线,
则选项A、B、C正确,
因为BD不一定平分,
所以选项D错误,
故选:D.
【点睛】
本题考查了三角形的中线、线段中点的定义、三角形的角平分线,掌握理解三角形中线的定义是解题关键.
7.B
【分析】
根据三角形角平分线的性质:三角形三条角平分线交于一点,且到三边的距离相等可以作判断.
【详解】
解:根据作图痕迹可知AE和BF为△ABC的角平分线,O为交点,
根据三角形三条角平分线交于一点,且到三边的距离相等可知点到三边的距离相等,故B选项正确,符合题意,其它选项皆不符合题意.
故选:B.
【点睛】
本题考查了基本作图-角的平分线、角平分线的性质,明确三角形的角平分线交于同一点,且交点到三边的距离相等.
8.D
【分析】
(1)根据三角形中线的性质可直接得出;(2)连接CO,利用中线性质及各三角形面积间的关系,得出,然后利用三角形等高及面积比,即可证明;(3)根据(2)即可得.
【详解】
(1)∵AD和BE是的中线,
∴,,
∴,
故(1)正确;
(2)连接CO,
∵E是AC中点,
∴,
又∵,
∴,
∴,
又∵,
∴,
即:,
∵与等高,面积比为2:1,
∴三角形的底边比,即:AO:OD=2:1,
∴,
故(2)正确;
(3)在(2)中已经证明,故(3)正确.
故选:D.
【点睛】
题目主要考察三角形中线的性质,理解中线的性质及理清题中各面积间的关系是解题关键.
9.C
【分析】
连接AE,由F为BE中点可得S△ABE=4,又由E为CD中点可得S△ADE=S△ADC,S△BDE=S△BDC,从而S△ABE=S△ADE+S△BDE=(S△ADC+S△BDC)=S△ABC=4,即可得到答案.
【详解】
连接AE,如图.
∵F为BE中点,S△ABF=2,
∴S△ABE=2S△ABF=2×2=4,
又E为CD中点,
∴S△ADE=S△ADC,S△BDE=S△BDC,
∴S△ABE=S△ADE+S△BDE
=S△ADC
+S△BDC,
=(S△ADC+S△BDC)
=S△ABC
=4,
故S△ABC=8.
故选C.
【点睛】
本题主要考查三角形的面积计算,解决本题的关键是要熟练掌握同底不等高的三角形面积比为高之比、同高不等底的三角形面积比为底之比.
10.D
【详解】
解:∵∠1=∠2,∴BD是△ABC的角平分线,∵∠3=∠4,∴CE是△BCD的角平分线,∠3=∠ACB,∴A、B、C正确.
CE不是△ABC的角平分线,故D错误.
故选D.
11.BE,
DE,
BF
【详解】
试题分析:(1)∵∠ABE=∠CBE
,∴BE是△ABC的角平分线;
(2)∵BD=CD,∴DE是△BCE的中线;
(3)∵∠ABE=∠CBE
,∴BF是△ABD的角平分线.
故答案为(1)BE,(2)DE,(3)BF.
12.5
cm
10
【分析】
熟悉三角形的角平分线、中线、高的概念:三角形的一个角的平分线和对边相交,顶点和交点间的线段叫三角形的角平分线;连接顶点和对边中点的线段叫三角形的中线;
三角形的高即从顶点向对边引垂线,顶点和垂足间的线段.根据概念,运用几何式子表示.
【详解】
解:∵在△ABC,AD是角平分线,AE是中线.AF是高,BC=10cm,
∴BE=5cm,
∵∠ABC=40°,∠ACB=60°,
∴∠BAC=180°?40°?60°=80°,
∴∠CAD=40°,
∵AF是高,
∴∠CAF=90°?60°=30°,
∴∠DAF=40°?30°=10°,
故答案为:5cm;10°.
【点睛】
本题考查了三角形的角平分线、中线和高.此题是一道基础题,能够根据三角形的中线、角平分线和高的概念得到线段、角之间的关系.
13.2.4
【分析】
根据面积相等可列式,代入相关数据求解即可.
【详解】
解:∵,,
∴
∵,,,
∴
故答案諀:2.4
【点睛】
此题主要考查了运用等积关系求线段的长,准确识图是解答本题的关键.
14.112
【分析】
首先根据∠ACB=68°可得∠1+∠PCB=68°,再根据三角形内角和定理和角平分线的定义等量代换可得答案.
【详解】
解:∵∠ACB=68°,
∴∠1+∠PCB=68°,
∵∠1=∠2,
∴∠2+∠PCB=68°,
∴∠BPC=180°-(∠2+∠PCB)=112°.
故答案为:112.
【点睛】
本题主要考查三角形的内角和定理和角平分线的定义,解决本题的关键是要熟练掌握三角形的内角和定理.
15.2cm
【详解】
试题分析:∵AD是△ABC中BC边上的中线,
∴BD=DC=BC,
∴△ABD和△ADC的周长的差
=(AB+BC+AD)-(AC+BC+AD)
=AB-AC
=5-3
=2(cm).
故答案为2cm.
16.(1)5cm;(2)不能,理由见解析
【分析】
(1)先求出AB=12cm,再利用ABC的周长求出AC=10,最后根据BD是AC边上的中线即可求得AD的长;
(2)先求出AB=16cm,再利用ABC的周长求出AC=4,然后根据三角形的三边关系即可判断此时的三角形是不存在的,由此可得答案.
【详解】
解:(1)∵AB=2BC,BC=6cm,
∴AB=12cm,
∵ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=28-12-6=10cm,
又∵BD是AC边上的中线,
∴AD=AC=5cm,
∴AD的长为5cm;
(2)不能求出AD的长,理由如下:
∵AB=2BC,BC=8cm,
∴AB=16cm,
∵ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=28-16-8=4cm,
∵4+8<16,
∴AC+BC<AB(与AC+BC>AB矛盾),
∴此时的ABC不存在,
∴此时不能求出AD的长.
【点睛】
本题考查了三角形的三边关系以及三角形的中线,三角形的周长等相关知识,注意运用三角形的三边关系解决(2)是解决本题的关键.
17.cm
【分析】
根据条件设BD=CD=1.5x,=2x,列出方程,即可求解.
【详解】
解:∵是边上的中线,,
∴设BD=CD=1.5x,=2x,
∴2x+3x+15=36,解得:x=,
∴BD=1.5x=cm.
【点睛】
此题考查三角形的中线的定义,设未知数,列出方程,是解题的关键.
18.见解析
【分析】
先根据题意可得,,得出的度数,进而求出的度数,再根据,得出的度数,根据对顶角相等求出的度数,再求出的度数,由此可得出结论.
【详解】
证明:是边上的高,
故,
,
∴∠BAD=45°,
,
,
,
,
在中,
,,
,
.
【点睛】
本题考查的是三角形内角和定理,熟知三角形内角和是是解答此题的关键.
19.(1);(2);(3)
【分析】
(1)利用直角三角形面积的两种求法求线段AM的长度即可;
(2)先求△ABC的面积,再根据△ANC与△ABN是等底同高的两个三角形,它们的面积相等,由此即可求得△ABN的面;
(3)由AN是中线,可得BN=CN,根据△ACN的周长-△ABN的周长=AC+AN+CN-(AB+BN+AN),化简可得△ACN的周长-△ABN的周长=AC-AB,即可求解.
【详解】
(1)∵,是边上的高,
∴,
∴,
即的长度为;
(2)如图,∵是直角三角形,,,,
∴.
又∵是边的中线,
∴,
∴,即,
∴.
∴的面积是.
(3)∵为边上的中线,
∴,
∴的周长-的周长,
即和的周长的差是.
【点睛】
三角形的高、中线和角平分线-同步课时训练学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图AD⊥BC于点D,那么图中以AD为高的三角形的个数有(
)
A.3
B.4
C.5
D.6
2.下面四个图形中,线段是的高的是(
)
A.
B.
C.
D.
3.钝角三角形三条高所在的直线交于( )
A.三角形内
B.三角形外
C.三角形的边上
D.不能确定
4.如图,已知于点,于点,于点,则中边上的高是(
)
A.
B.
C.
D.
5.下列说法正确的个数有(
)
①三角形的高、中线、角平分线都是线段;
②三角形的三条角平分线都在三角形内部,且交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
A.1个
B.2个
C.3个
D.4个
6.如图,D,E分别是的边AC,BC的中点,则下列说法错误的是(
)
A.DE是的中线
B.BD是的中线
C.
D.BD是的角平分线
7.如图,与交于点,点在上,根据尺规作图的痕迹,判断下列说法正确的是(
)
A.
B.点到三边的距离相等
C.
D.
8.如图,和是的中线,与交于点下列结论正确的有(
)个.
(1)
(2)
(3)S四边形DOEC
A.个
B.个
C.个
D.个
9.如图,△ABF的面积是2,D是AB边上任意一点,E是CD中点,F是BE中点,△ABC的面积是( )
A.4
B.6
C.8
D.16
10.如图,
∠1=∠2,∠3=∠4,下列结论错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
二、填空题
11.如图,在△ABC中,BD=CD,∠ABE=∠CBE,BE交AD于点F.
(1)______是△ABC的角平分线;
(2)______是△BCE的中线;
(3)______是△ABD的角平分线.
12.如图,在△ABC,AD
是角平分线,AE
是中线,AF
是高.如果BC=10cm,那么
BE=_____;∠ABC=40°,∠ACB=60°,那么∠DAF=_____°.
13.如图,在三角形中,,,垂足为,,,,则______.
14.如图,在△ABC中,∠ACB=68°,∠1=∠2.若P为△ABC的角平分线BP、CP的交点,则∠BPC=__________°.
15.AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,△ABD与△ACD的周长之差为_________.
三、解答题
16.如图,ABC的周长是28cm,AB=2BC,BD是AC边上的中线.
(1)当BC=6cm时,求AD的长;
(2)当BC=8cm时,能否求出AD的长?若能,则请求出AD的长度;若不能,请说明理由.
17.如图,在的周长为,是边上的中线,,,求的长.
18.如图,在中,是边上的高,是边上一点,与交于点,,,.求证:.
19.如图,已知,分别是的高和中线,,,,.试求:
(1)的长;
(2)的面积;
(3)和的周长差.
参考答案
1.D
【详解】
结合三角形高的定义可知,以AD为高的三角形有:△ABD,△ABE,△ABC,△ADE,△ADC,△AEC,共6个.
故选D.
2.D
【分析】
根据三角形高的定义进行判断.
【详解】
解:线段AD是△ABC的高,则过点A作对边BC的垂线,则垂线段AD为△ABC的高.
选项A、B、C错误,
故选:D.
【点睛】
本题考查了三角形的高:三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.
3.B
【分析】
由图形可知:钝角三角形三条高所在的直线交于三角形外.
【详解】
解:如图可知:钝角△ABC三边的高交于三角形外部一点D,
即钝角三角形三条高所在的直线交于三角形外,
故选:B.
【点睛】
本题考查三角形的高线的交点问题,解答的关键是会画三角形的高线,并能根据三角形的形状得出三条高线所在的直线的交点与三角形的关系.
4.D
【分析】
从三角形的一个顶点向它的对边引垂线,顶点和垂足间的线段叫做三角形的高.根据此概念求解即可.
【详解】
A、CF⊥AB,∴线段CF是△ABC中AB边上的高,此选项不符合题意;
B、BE⊥AC,∴线段BE是△ABC中AC边上的高,此选项不符合题意;
C、CD不是△ABC的高,此选项不符合题意;
D、AD⊥BC,∴线段AD是△ABC中BC边上的高,此选项符合题意;
故选:D.
【点睛】
本题主要考查了三角形的高.准确识图并熟记三角形高的定义是解题的关键.
5.C
【分析】
根据三角形的三条中线都在三角形内部;三角形的三条角平分线都在三角形内部;三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上即可作答.
【详解】
解:①三角形的中线、角平分线、高都是线段,故正确;
②三角形的三条角平分线都在三角形内部,且交于同一点,故正确;
③钝角三角形的高有两条在三角形外部,故错误;
④三角形的一条中线把该三角形分成面积相等的两部分,故正确.
所以正确的有3个.
故选:C.
【点睛】
本题考查对三角形的中线、角平分线、高的正确理解,熟练掌握三角形的中线、角平分线、高的概念是解决本题的关键.
6.D
【分析】
根据三角形的中线、线段中点的定义、三角形的角平分线判断即可得.
【详解】
点D,E分别是的边AC,BC的中点,
,
是的边AC上的中线,DE是的边BC上的中线,
则选项A、B、C正确,
因为BD不一定平分,
所以选项D错误,
故选:D.
【点睛】
本题考查了三角形的中线、线段中点的定义、三角形的角平分线,掌握理解三角形中线的定义是解题关键.
7.B
【分析】
根据三角形角平分线的性质:三角形三条角平分线交于一点,且到三边的距离相等可以作判断.
【详解】
解:根据作图痕迹可知AE和BF为△ABC的角平分线,O为交点,
根据三角形三条角平分线交于一点,且到三边的距离相等可知点到三边的距离相等,故B选项正确,符合题意,其它选项皆不符合题意.
故选:B.
【点睛】
本题考查了基本作图-角的平分线、角平分线的性质,明确三角形的角平分线交于同一点,且交点到三边的距离相等.
8.D
【分析】
(1)根据三角形中线的性质可直接得出;(2)连接CO,利用中线性质及各三角形面积间的关系,得出,然后利用三角形等高及面积比,即可证明;(3)根据(2)即可得.
【详解】
(1)∵AD和BE是的中线,
∴,,
∴,
故(1)正确;
(2)连接CO,
∵E是AC中点,
∴,
又∵,
∴,
∴,
又∵,
∴,
即:,
∵与等高,面积比为2:1,
∴三角形的底边比,即:AO:OD=2:1,
∴,
故(2)正确;
(3)在(2)中已经证明,故(3)正确.
故选:D.
【点睛】
题目主要考察三角形中线的性质,理解中线的性质及理清题中各面积间的关系是解题关键.
9.C
【分析】
连接AE,由F为BE中点可得S△ABE=4,又由E为CD中点可得S△ADE=S△ADC,S△BDE=S△BDC,从而S△ABE=S△ADE+S△BDE=(S△ADC+S△BDC)=S△ABC=4,即可得到答案.
【详解】
连接AE,如图.
∵F为BE中点,S△ABF=2,
∴S△ABE=2S△ABF=2×2=4,
又E为CD中点,
∴S△ADE=S△ADC,S△BDE=S△BDC,
∴S△ABE=S△ADE+S△BDE
=S△ADC
+S△BDC,
=(S△ADC+S△BDC)
=S△ABC
=4,
故S△ABC=8.
故选C.
【点睛】
本题主要考查三角形的面积计算,解决本题的关键是要熟练掌握同底不等高的三角形面积比为高之比、同高不等底的三角形面积比为底之比.
10.D
【详解】
解:∵∠1=∠2,∴BD是△ABC的角平分线,∵∠3=∠4,∴CE是△BCD的角平分线,∠3=∠ACB,∴A、B、C正确.
CE不是△ABC的角平分线,故D错误.
故选D.
11.BE,
DE,
BF
【详解】
试题分析:(1)∵∠ABE=∠CBE
,∴BE是△ABC的角平分线;
(2)∵BD=CD,∴DE是△BCE的中线;
(3)∵∠ABE=∠CBE
,∴BF是△ABD的角平分线.
故答案为(1)BE,(2)DE,(3)BF.
12.5
cm
10
【分析】
熟悉三角形的角平分线、中线、高的概念:三角形的一个角的平分线和对边相交,顶点和交点间的线段叫三角形的角平分线;连接顶点和对边中点的线段叫三角形的中线;
三角形的高即从顶点向对边引垂线,顶点和垂足间的线段.根据概念,运用几何式子表示.
【详解】
解:∵在△ABC,AD是角平分线,AE是中线.AF是高,BC=10cm,
∴BE=5cm,
∵∠ABC=40°,∠ACB=60°,
∴∠BAC=180°?40°?60°=80°,
∴∠CAD=40°,
∵AF是高,
∴∠CAF=90°?60°=30°,
∴∠DAF=40°?30°=10°,
故答案为:5cm;10°.
【点睛】
本题考查了三角形的角平分线、中线和高.此题是一道基础题,能够根据三角形的中线、角平分线和高的概念得到线段、角之间的关系.
13.2.4
【分析】
根据面积相等可列式,代入相关数据求解即可.
【详解】
解:∵,,
∴
∵,,,
∴
故答案諀:2.4
【点睛】
此题主要考查了运用等积关系求线段的长,准确识图是解答本题的关键.
14.112
【分析】
首先根据∠ACB=68°可得∠1+∠PCB=68°,再根据三角形内角和定理和角平分线的定义等量代换可得答案.
【详解】
解:∵∠ACB=68°,
∴∠1+∠PCB=68°,
∵∠1=∠2,
∴∠2+∠PCB=68°,
∴∠BPC=180°-(∠2+∠PCB)=112°.
故答案为:112.
【点睛】
本题主要考查三角形的内角和定理和角平分线的定义,解决本题的关键是要熟练掌握三角形的内角和定理.
15.2cm
【详解】
试题分析:∵AD是△ABC中BC边上的中线,
∴BD=DC=BC,
∴△ABD和△ADC的周长的差
=(AB+BC+AD)-(AC+BC+AD)
=AB-AC
=5-3
=2(cm).
故答案为2cm.
16.(1)5cm;(2)不能,理由见解析
【分析】
(1)先求出AB=12cm,再利用ABC的周长求出AC=10,最后根据BD是AC边上的中线即可求得AD的长;
(2)先求出AB=16cm,再利用ABC的周长求出AC=4,然后根据三角形的三边关系即可判断此时的三角形是不存在的,由此可得答案.
【详解】
解:(1)∵AB=2BC,BC=6cm,
∴AB=12cm,
∵ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=28-12-6=10cm,
又∵BD是AC边上的中线,
∴AD=AC=5cm,
∴AD的长为5cm;
(2)不能求出AD的长,理由如下:
∵AB=2BC,BC=8cm,
∴AB=16cm,
∵ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=28-16-8=4cm,
∵4+8<16,
∴AC+BC<AB(与AC+BC>AB矛盾),
∴此时的ABC不存在,
∴此时不能求出AD的长.
【点睛】
本题考查了三角形的三边关系以及三角形的中线,三角形的周长等相关知识,注意运用三角形的三边关系解决(2)是解决本题的关键.
17.cm
【分析】
根据条件设BD=CD=1.5x,=2x,列出方程,即可求解.
【详解】
解:∵是边上的中线,,
∴设BD=CD=1.5x,=2x,
∴2x+3x+15=36,解得:x=,
∴BD=1.5x=cm.
【点睛】
此题考查三角形的中线的定义,设未知数,列出方程,是解题的关键.
18.见解析
【分析】
先根据题意可得,,得出的度数,进而求出的度数,再根据,得出的度数,根据对顶角相等求出的度数,再求出的度数,由此可得出结论.
【详解】
证明:是边上的高,
故,
,
∴∠BAD=45°,
,
,
,
,
在中,
,,
,
.
【点睛】
本题考查的是三角形内角和定理,熟知三角形内角和是是解答此题的关键.
19.(1);(2);(3)
【分析】
(1)利用直角三角形面积的两种求法求线段AM的长度即可;
(2)先求△ABC的面积,再根据△ANC与△ABN是等底同高的两个三角形,它们的面积相等,由此即可求得△ABN的面;
(3)由AN是中线,可得BN=CN,根据△ACN的周长-△ABN的周长=AC+AN+CN-(AB+BN+AN),化简可得△ACN的周长-△ABN的周长=AC-AB,即可求解.
【详解】
(1)∵,是边上的高,
∴,
∴,
即的长度为;
(2)如图,∵是直角三角形,,,,
∴.
又∵是边的中线,
∴,
∴,即,
∴.
∴的面积是.
(3)∵为边上的中线,
∴,
∴的周长-的周长,
即和的周长的差是.
【点睛】
