2021-2022学年华东师大版九年级数学上册23.3相似三角形课件(31张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学上册23.3相似三角形课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
第23章图形的相似
23.3相似三角形
九年级华师版上册
1.比例线段:对于四条线段
a,b,c,d,如果有
=
那么这四条线段成比例
2.比例的性质
(1)基本性质:
(
b≠0,d≠0
)
.
(2)合比性质:
=
(b≠0,d≠0)
(3)等比性质:
(
b,d…n≠0
).
温故知新
ad=bc
3.平行线分线段成比例
(1)基本事实:两条直线被一组平行线所截,所得的对应线段
_.
(2)推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段
成比例
4.什么是黄金分割?
5什么叫做相似多边形?什么叫做相似多边形的相似比?
6.相似多边形的性质是什么?
成比例
1、相似三角形的概念,会根据概念判断两个三角形是否相似。
2、利用平行线判定两个三角形相似的定理。
学习目标
问题1:图中的两个图形有什么关系?
它们还全等吗?
什么样的图形是全等图形?
形状相同,
大小也相同
探究新知
问题2:什么样的图形是相似图形?
相似图形
相似图形
相似图形
相似图形
探究新知
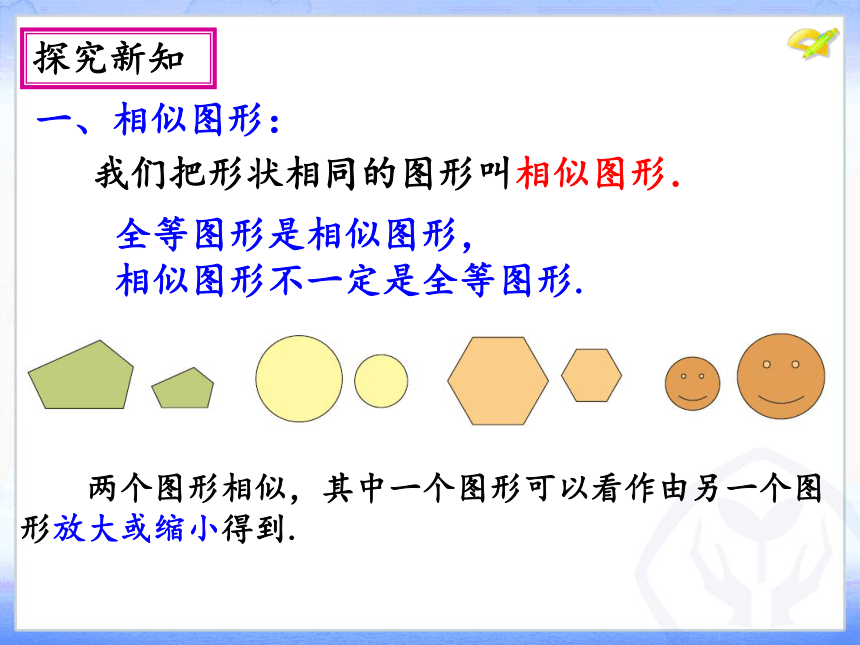
我们把形状相同的图形叫相似图形.
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
一、相似图形:
探究新知
全等图形是相似图形,
相似图形不一定是全等图形.
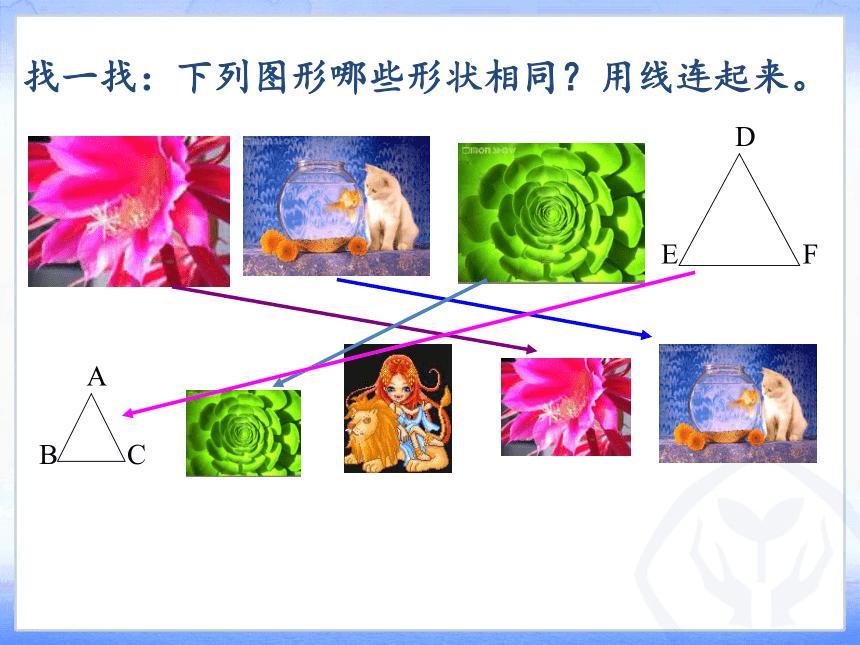
找一找:下列图形哪些形状相同?用线连起来。
B
C
A
D
E
F
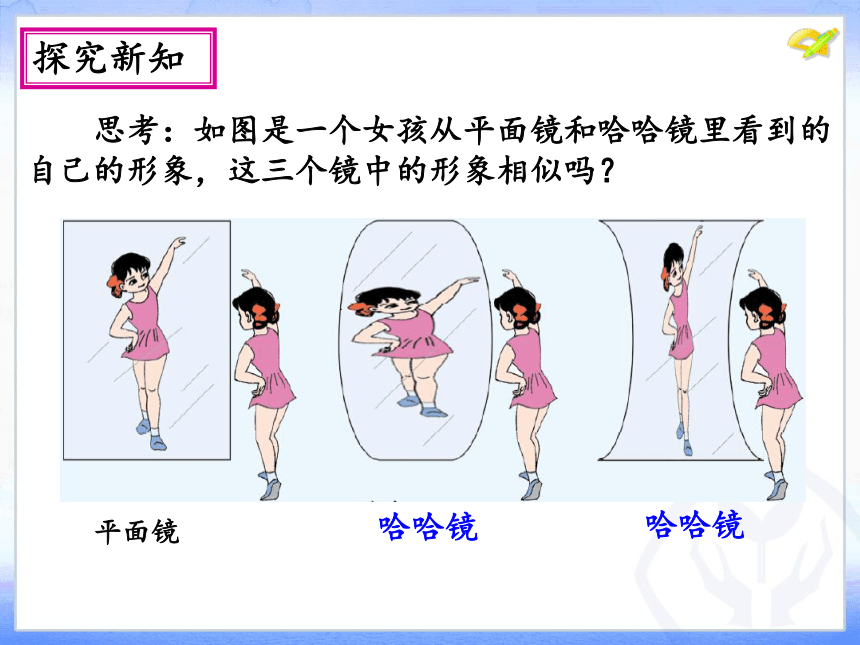
思考:如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这三个镜中的形象相似吗?
哈哈镜
探究新知
平面镜
哈哈镜
多边形
由在同一平面且不在同一直线上的多条线段首尾顺次连结且不相交所组成的图形叫做多边形。
探究新知
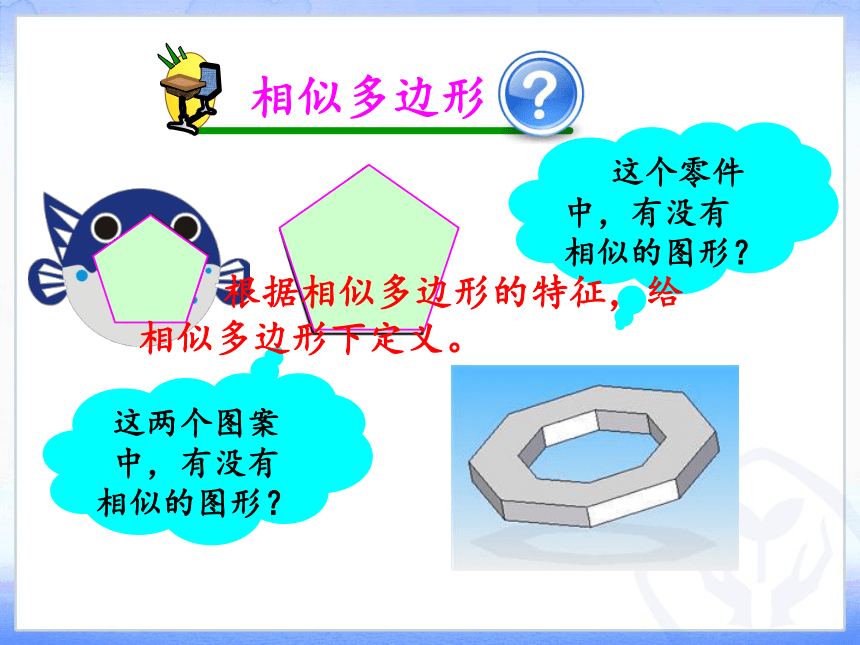
相似多边形
这两个图案中,有没有相似的图形?
这个零件中,有没有相似的图形?
根据相似多边形的特征,给相似多边形下定义。
A
B
C
A1
B1
C1
正三角形
缩小
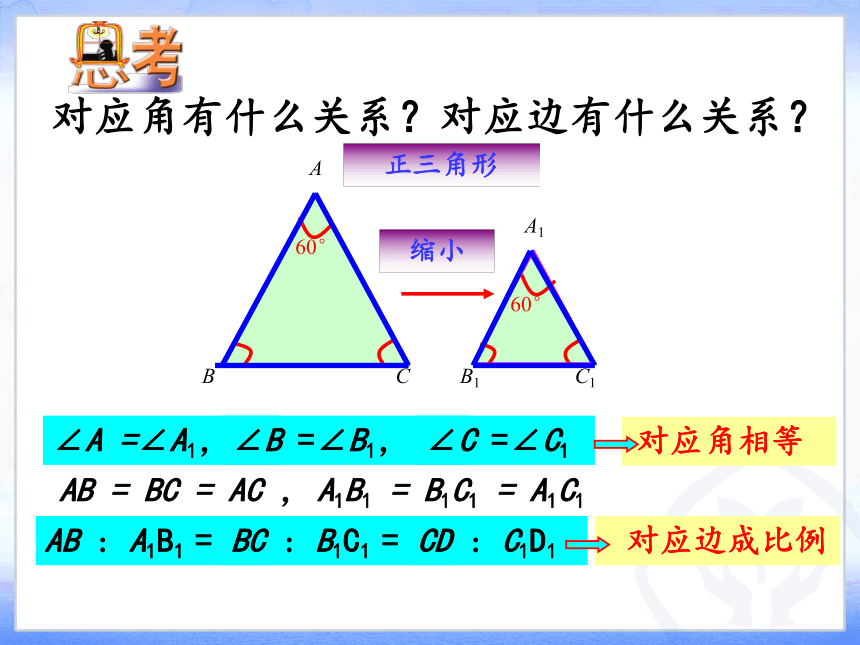
对应角有什么关系?对应边有什么关系?
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1
AB
:
A1B1
=
BC
:
B1C1
=
CD
:
C1D1
AB
=
BC
=
AC
,
A1B1
=
B1C1
=
A1C1
60°
60°
对应角相等
对应边成比例
正八边形
放大
对应角有什么关系?
150°
150°
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1
对应角相等
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
∠D
=∠D1,
∠E
=∠E1,
∠F
=∠F1
正八边形
放大
对应边有什么关系?
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
AB
=
BC
=
CD
=
DE
=
EF
=
FA
,
A1B1
=
B1C1
=
C1D1
=
D1E1
=
E1F1
=
F1A1
对应边成比例
A1B1
AB
B1C1
BC
=
C1D1
CD
D1E1
DE
=
E1F1
EF
F1A1
FA
=
=
=
A
B
C
D
A1
B1
C1
D1
请分别量出这两个不规则四边形各内角的度数,求出对应边的长度。
对应角有什么关系?
对应边有什么关系?
不规则四边形
缩小
相似多边形
知识要点
(对应边的比相等)
相似比
相似多边形对应边的比。
(k
>
0)
若相似比k
=1
,相似图形有什么关系?
对应角相等,对应边成比例。
全等是一种特殊的相似。
当相似比k
=1时,
相似图形即是全等图形。
A
B
C
F
E
D
A1
B1
C1
F1
E1
D1
六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为
k1=
2
:
1,
对应边
AB:A1B1=
2
:
1
。
相似比与叙述的顺序有关。
相似多边形
各对应角相等、各对应边成比例的多边形叫做相似多边形.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
边数相同。
所有对应边成比例。
所有对应角相等。
两个多边形相似的判定条件
相似六边形
相似多边形的对应高
相似多边形的对应角平分线
相似多边形的对应中线
相似多边形的对应对角线
A
B
C
A1
B1
C1
相似多边形的对应三角形
相似多边形的性质
相似多边形对应高的比、对应角平分线的比、对应中线的比、对应周长的比都等于相似比。
相似多边形对应对角线的比等于相似比。
相似多边形对应三角形相似,且相似比等于相似多边形的相似比。
相似多边形面积的比等于相似比的平方。
相似多边形对应三角形面积的比等于相似多边形的相似比的平方。
题型1
判断两个多边形是否相似
3
正方形
3
4
4
菱形
解:
∵
正方形,菱形的四条边都相等.
∴
它们的对应边成比例,k
=
3
:
4.
∵
正方形的四个内角均为直角,
而菱形的内角有钝角有锐角.
∴
它们的对应角不相等.
∴
这一组图形不相似.
例题
3
正方形
3
6
8
长方形
解:∵
正方形和矩形的四个内角都是直角.
∴
它们的对应角相等.
∵
对应边
3
:
6
≠
3
:
8.
∴
它们的对应边不成比例.
∴
这一组图形不相似.
例题
解:
∵
矩形的每个内角都等于90o.
∴
∠A
=∠E
=
90°,∠B
=∠F
=
90°
∠C
=∠G
=
90°,∠D
=∠H
=
90°
∴
它们的对应角相等.
∵
EH:AD=300:(300+2×7.5)=20/21.
EF:AB
=150:(150+2×7.5)=10/11.
∴
EH:AD≠EF:AB.
∴
它们的对应边不成比例.
∴
矩形ABCD和矩形EFGH不相似.
一块长
3m,宽1.5m的矩形黑板,镶其外围的木质边宽7.5cm。边框内外边缘所组成的矩形相似吗?为什么?
例题
课堂小结
1.
相似图形:
形状相同的图形。
2.
相似多边形:
对应角相等,对应边成比例。
相似多边形对应边的比。
3.
相似比:
第23章图形的相似
23.3相似三角形
九年级华师版上册
1.比例线段:对于四条线段
a,b,c,d,如果有
=
那么这四条线段成比例
2.比例的性质
(1)基本性质:
(
b≠0,d≠0
)
.
(2)合比性质:
=
(b≠0,d≠0)
(3)等比性质:
(
b,d…n≠0
).
温故知新
ad=bc
3.平行线分线段成比例
(1)基本事实:两条直线被一组平行线所截,所得的对应线段
_.
(2)推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段
成比例
4.什么是黄金分割?
5什么叫做相似多边形?什么叫做相似多边形的相似比?
6.相似多边形的性质是什么?
成比例
1、相似三角形的概念,会根据概念判断两个三角形是否相似。
2、利用平行线判定两个三角形相似的定理。
学习目标
问题1:图中的两个图形有什么关系?
它们还全等吗?
什么样的图形是全等图形?
形状相同,
大小也相同
探究新知
问题2:什么样的图形是相似图形?
相似图形
相似图形
相似图形
相似图形
探究新知
我们把形状相同的图形叫相似图形.
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
一、相似图形:
探究新知
全等图形是相似图形,
相似图形不一定是全等图形.
找一找:下列图形哪些形状相同?用线连起来。
B
C
A
D
E
F
思考:如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这三个镜中的形象相似吗?
哈哈镜
探究新知
平面镜
哈哈镜
多边形
由在同一平面且不在同一直线上的多条线段首尾顺次连结且不相交所组成的图形叫做多边形。
探究新知
相似多边形
这两个图案中,有没有相似的图形?
这个零件中,有没有相似的图形?
根据相似多边形的特征,给相似多边形下定义。
A
B
C
A1
B1
C1
正三角形
缩小
对应角有什么关系?对应边有什么关系?
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1
AB
:
A1B1
=
BC
:
B1C1
=
CD
:
C1D1
AB
=
BC
=
AC
,
A1B1
=
B1C1
=
A1C1
60°
60°
对应角相等
对应边成比例
正八边形
放大
对应角有什么关系?
150°
150°
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1
对应角相等
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
∠D
=∠D1,
∠E
=∠E1,
∠F
=∠F1
正八边形
放大
对应边有什么关系?
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
AB
=
BC
=
CD
=
DE
=
EF
=
FA
,
A1B1
=
B1C1
=
C1D1
=
D1E1
=
E1F1
=
F1A1
对应边成比例
A1B1
AB
B1C1
BC
=
C1D1
CD
D1E1
DE
=
E1F1
EF
F1A1
FA
=
=
=
A
B
C
D
A1
B1
C1
D1
请分别量出这两个不规则四边形各内角的度数,求出对应边的长度。
对应角有什么关系?
对应边有什么关系?
不规则四边形
缩小
相似多边形
知识要点
(对应边的比相等)
相似比
相似多边形对应边的比。
(k
>
0)
若相似比k
=1
,相似图形有什么关系?
对应角相等,对应边成比例。
全等是一种特殊的相似。
当相似比k
=1时,
相似图形即是全等图形。
A
B
C
F
E
D
A1
B1
C1
F1
E1
D1
六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为
k1=
2
:
1,
对应边
AB:A1B1=
2
:
1
。
相似比与叙述的顺序有关。
相似多边形
各对应角相等、各对应边成比例的多边形叫做相似多边形.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
边数相同。
所有对应边成比例。
所有对应角相等。
两个多边形相似的判定条件
相似六边形
相似多边形的对应高
相似多边形的对应角平分线
相似多边形的对应中线
相似多边形的对应对角线
A
B
C
A1
B1
C1
相似多边形的对应三角形
相似多边形的性质
相似多边形对应高的比、对应角平分线的比、对应中线的比、对应周长的比都等于相似比。
相似多边形对应对角线的比等于相似比。
相似多边形对应三角形相似,且相似比等于相似多边形的相似比。
相似多边形面积的比等于相似比的平方。
相似多边形对应三角形面积的比等于相似多边形的相似比的平方。
题型1
判断两个多边形是否相似
3
正方形
3
4
4
菱形
解:
∵
正方形,菱形的四条边都相等.
∴
它们的对应边成比例,k
=
3
:
4.
∵
正方形的四个内角均为直角,
而菱形的内角有钝角有锐角.
∴
它们的对应角不相等.
∴
这一组图形不相似.
例题
3
正方形
3
6
8
长方形
解:∵
正方形和矩形的四个内角都是直角.
∴
它们的对应角相等.
∵
对应边
3
:
6
≠
3
:
8.
∴
它们的对应边不成比例.
∴
这一组图形不相似.
例题
解:
∵
矩形的每个内角都等于90o.
∴
∠A
=∠E
=
90°,∠B
=∠F
=
90°
∠C
=∠G
=
90°,∠D
=∠H
=
90°
∴
它们的对应角相等.
∵
EH:AD=300:(300+2×7.5)=20/21.
EF:AB
=150:(150+2×7.5)=10/11.
∴
EH:AD≠EF:AB.
∴
它们的对应边不成比例.
∴
矩形ABCD和矩形EFGH不相似.
一块长
3m,宽1.5m的矩形黑板,镶其外围的木质边宽7.5cm。边框内外边缘所组成的矩形相似吗?为什么?
例题
课堂小结
1.
相似图形:
形状相同的图形。
2.
相似多边形:
对应角相等,对应边成比例。
相似多边形对应边的比。
3.
相似比:
