2021—2022学年人教版数学九年级上册第22章二次函数复习课件(42张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学九年级上册第22章二次函数复习课件(42张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 21:03:15 | ||
图片预览








文档简介
(共42张PPT)
第
22
章
二次函数
Quadratic
Function
回顾:正比例函数和一次函数
我们学过哪些函数?
一次函数
形如
与轴的交点坐标为,与轴的交点坐标为
当时,
随的增大而增大;
当时,
随的增大而减小;
当时,函数图像与轴交于正半轴;
当时,函数图像与轴交于负半轴;
当时,函数图像过原点,是个正比例函数。
解析式的确定:待定系数法(设、代、解,得,验)
平移:上加下减、左加右减
引入:
个球队参加比赛,每两队之间进行一场比赛。比赛的场次数与球队数有什么关系?
每个队要与其他个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛是同一场比赛
所以比赛的场次数
即
像上式这样,比赛的场次数与球队数的关系,对于的每一个值,
都有一个对应值,那么我们说,是的函数。
22.1
二次函数的图像和性质
22.1
二次函数的图像和性质
定义:形如的函数。其中,是自变量,
分别是函数解析式的二次项系数、一次项系数和常数项。
注意:每项的系数包括它前面的符号
那么,这个函数的图像是怎么样的呢?
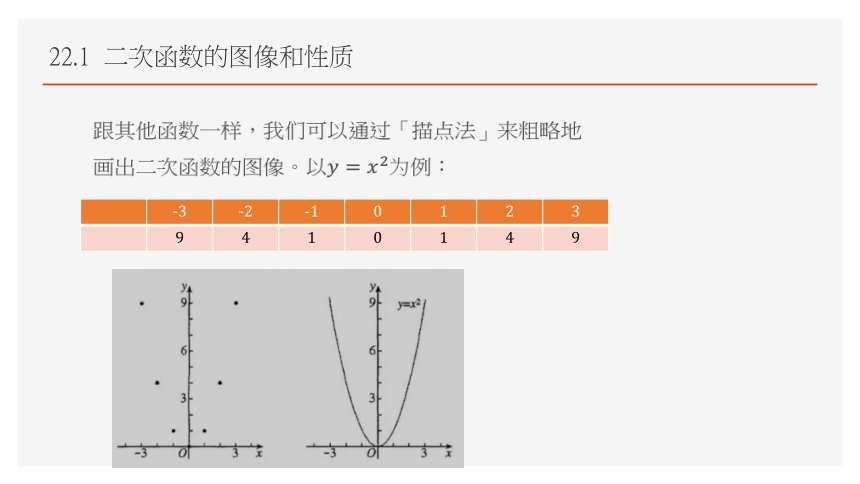
跟其他函数一样,我们可以通过「描点法」来粗略地画出二次函数的图像。以为例:
22.1
二次函数的图像和性质
-3
-2
-1
0
1
2
3
9
4
1
0
1
4
9
22.1
二次函数的图像和性质
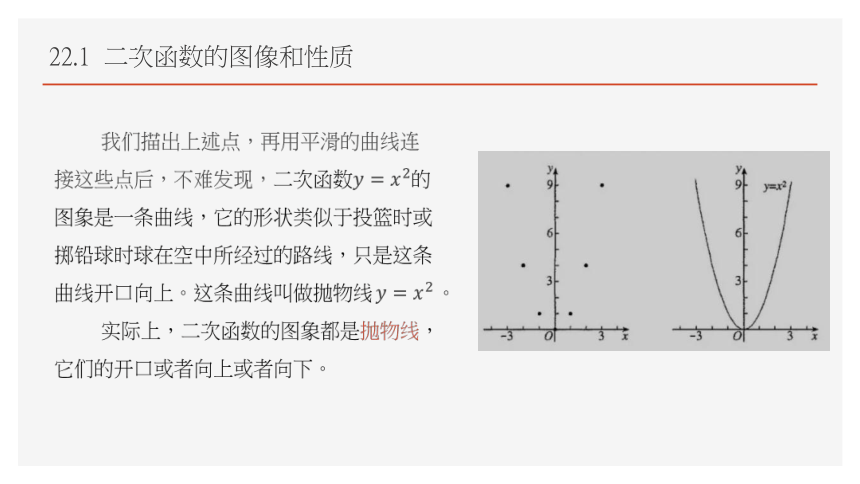
我们描出上述点,再用平滑的曲线连接这些点后,不难发现,二次函数的图象是一条曲线,它的形状类似于投篮时或掷铅球时球在空中所经过的路线,只是这条曲线开口向上。这条曲线叫做抛物线。
实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下。
22.1
二次函数的图像和性质
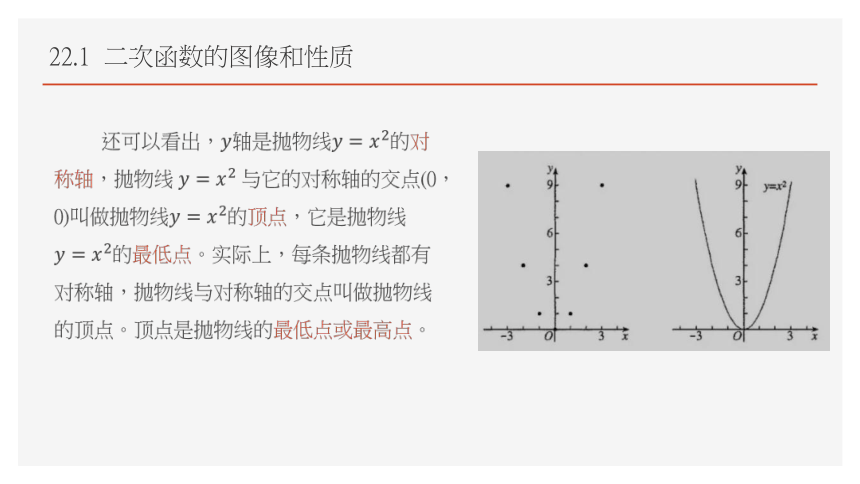
还可以看出,轴是抛物线的对称轴,抛物线与它的对称轴的交点(0,0)叫做抛物线的顶点,它是抛物线的最低点。实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的顶点。顶点是抛物线的最低点或最高点。
22.1
二次函数的图像和性质
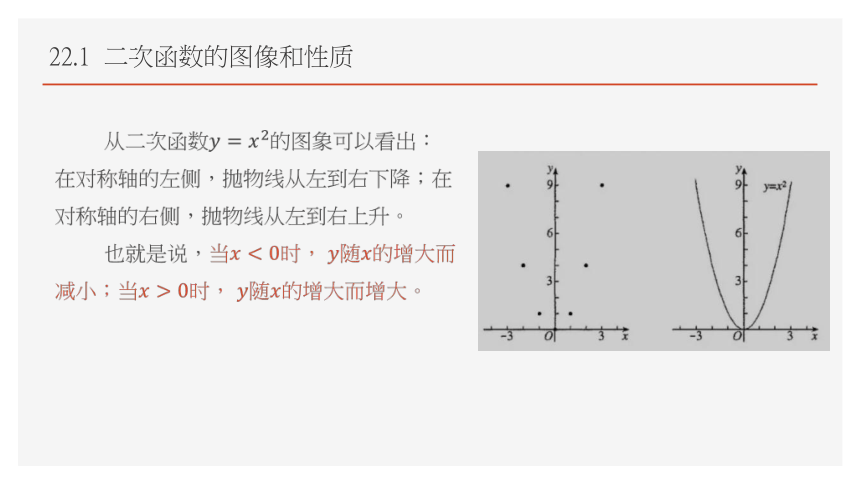
从二次函数的图象可以看出:在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛物线从左到右上升。
也就是说,当时,
随的增大而减小;当时,
随的增大而增大。
22.1
二次函数的图像和性质
我们已经知道的图象,那么的图像与有何异同呢?
一般地,当时,抛物线的开口向上,对称轴是轴,顶点是原点,顶点是抛物线的最低点,
越大,抛物线的开口越小。类似地,我们可以研究当时,二次函数的图象和性质.
22.1
二次函数的图像和性质
一般地,当时,抛物线的开口向下,对称轴是轴,顶点是原点,顶点是抛物线的最低点,
越大,抛物线的开口越小。
22.1
二次函数的图像和性质
的图像我们已经了解了,在之前学习其他函数的时候,我们学习了函数的平移:「上加下减,左加右减」,这个口诀对二次函数一样适用。
首先我们先来对他进行上下平移,试着用描点法画出和的图像。
可以看出,把向上平移个单位长度,就得到抛物线;把抛物线向下平移个单位长度,就得到抛物线。
22.1
二次函数的图像和性质
,对它进行左右平移呢?
试着画出和的图像。
可以看出,把向左平移个单位长度,就得到;把向右平移个单位长度,就得到抛物线。
他们的开口都向下,其中的对称轴是,顶点是;
的对称轴是,顶点是。
22.1
二次函数的图像和性质
归纳:通过上面的几种变形我们发现,
与的形状相同,但是位置不同,把进行平移后,就可以得到抛物线
。
抛物线
有如下特点
开口方向:当,开口向上;当时,开口向下
对称轴:
顶点:
增减性:
1、若,当时,
随增大而减小,当时,
随增大而增大;
2、若,当时,
随增大而增大,当时,
随增大而减小。
22.1
二次函数的图像和性质
例1:要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
[解析]
如图,以水管与地面交点为原点,原点与水柱落地处所在直线为轴,水管所在直线为轴,建立直角坐标系。
点是图中这段抛物线的顶点,因此可设这段抛物线对应的函数解析式是
∵抛物线经过点,可得
解得
因此
当时,
也就是说,水管应2.25m长。
22.1
二次函数的图像和性质
我们知道,二次函数解析式中一般式是,刚刚研究的都是顶点式:的函数图像,那么他们之间有什么联系呢?
事实上,我们可以把通过配方法化成的形式,即
因此,抛物线的对称轴是,顶点是。
22.1
二次函数的图像和性质
如图所示,从二次函数的图像可以看出:
若,当时,
随增大而减小,当时,
随增大而增大;
若,当时,
随增大而增大,当时,
随增大而减小。
22.1
二次函数的图像和性质
二次函数解析式归纳:
一般式:
顶点式:
22.1
二次函数的图像和性质
例2:分别写出抛物线与的开口方向、对称轴和顶点。
[答案]
开口方向
对称轴
顶点
向上
或轴
向下
或轴
22.1
二次函数的图像和性质
例3:分别写出抛物线、、
的开口方向、对称轴和顶点。
[答案]
开口方向
对称轴
顶点
向上
或轴
向下
向上
22.1
二次函数的图像和性质
我们之前学过一次函数解析式的确定,已知两点就可以确定一条直线的解析式。那么,二次函数的解析式该如何确定呢?
确定一次函数,即写出这个一次函数的解析式,需求出,的值。用待定系数法,由两点(两点的连线不与坐标轴平行)的坐标,列出关于,的二元一次方程组就可以求出的值。
类似地,确定二次函数,即写出这个二次函数的解析式,需求出的值。由不共线三点(三点不在同一直线上)的坐标,列出关于的三元一次方程组就可以求出的值。
22.1
二次函数的图像和性质
例4:已知抛物线过三点,求该抛物线的函数解析式。
[解析]
因为抛物线过三点,所以可以得到关于阿的三元一次方程组:
解这个方程组,得
所求二次函数是
22.1
二次函数的图像和性质
思考:是不是一条抛物线至少需要三个点才能确定他的解析式呢?
我们知道二次函数解析式的一般式是,他有三个参数,就需要三个方程才能求解。
但是对于他的顶点式
来说,顶点坐标是,那么当我们知道顶点坐标时,顶点式中就只剩一个参数是未知的了,此时只需要抛物线上除顶点外的一点就可以求出它的解析式。
22.1
二次函数的图像和性质
例5:已知抛物线上两点,其中点是该抛物线的顶点,求该抛物线的函数解析式。
[解析]
∵抛物线的顶点坐标为
∴设抛物线解析式为
把点
代入中
得
解得
∴该抛物线的函数解析式为
22.2
二次函数与一元二次方程
22.2
二次函数与一元二次方程
例6:如右下图所示,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度
h(单位:m)与飞行时间(单位:s)之间具有函数关系
(1)小球的飞行高度能否达到15m?如果能,需要多少飞行时间?
解:依题得
即
解得
,
∴当小球飞行1s和3s时,它的飞行高度为15m。
22.2
二次函数与一元二次方程
例6:如右下图所示,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度
h(单位:m)与飞行时间(单位:s)之间具有函数关系
(2)小球的飞行高度能否达到20m?如果能,需要多少飞行时间?
解:依题得
即
解得
∴当小球飞行2s时,它的飞行高度为20m。
22.2
二次函数与一元二次方程
例6:如右下图所示,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度
h(单位:m)与飞行时间(单位:s)之间具有函数关系
(3)小球的飞行高度能否达到20.5m?为什么?
解:依题得
即
因为
∴方程无实数根,即小球的飞行高度达不到20.5m。
22.2
二次函数与一元二次方程
例6:如右下图所示,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度
h(单位:m)与飞行时间(单位:s)之间具有函数关系
(4)小球从飞出到落地要用多少时间?
解:小球飞出及落地时的高度都为0m,
即
即
解得
,
∴小球在0s时起飞,在4s时落地,从飞出到落地要用4s。
22.2
二次函数与一元二次方程
从上面可以看出,二次函数与一元二次方程联系密切。例如,已知二次函数的值为,求自变量的值,可以看作解一元二次方程(即)。反过来,解方程又可以看作已知二次函数的值为,求自变量的值。
一般地,我们可以利用二次函数深入讨论一元二次方程
。
22.2
二次函数与一元二次方程
例7:下列二次函数的图象与轴有公共点吗?如果有,公共点的横坐标是多少?当取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
这些函数的图像如右下图所示。
(1)
(2)
(3)
[解析]
抛物线与轴有两个公共点
它们的横坐标是
当取公共点的横坐标时,函数值是
由此得出方程的根是
22.2
二次函数与一元二次方程
例7:下列二次函数的图象与轴有公共点吗?如果有,公共点的横坐标是多少?当取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
这些函数的图像如右下图所示。
(1)
(2)
(3)
[解析]
抛物线与轴有一个公共点
这点的横坐标是
当时,函数值是
由此得出方程有两个相等的实数根
22.2
二次函数与一元二次方程
例7:下列二次函数的图象与轴有公共点吗?如果有,公共点的横坐标是多少?当取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
这些函数的图像如右下图所示。
(1)
(2)
(3)
[解析]
抛物线与工轴没有公共点
由此可知,方程没有实数根
22.2
二次函数与一元二次方程
例7:下列二次函数的图象与轴有公共点吗?如果有,公共点的横坐标是多少?当取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
这些函数的图像如右下图所示。
(1)
(2)
(3)
[归纳]
由二次函数图象与?轴位置关系的情况,可以得出相应一元二次方程的根;
反过来,由一元二次方程的根的情况,也可以确定相应二次函数图象与轴的位置关系。
22.3
实际问题与二次函数
22.3
实际问题与二次函数
对于某些实际问题,如果其中变量之间的关系可以用二次函数模型来刻画,那么我们就可以利用二次函数的图象和性质来研究。
例8:从地面竖直向上抛出一小球,小球的高度(单位:)与小球的运动时间(单位:)之间的关系式是小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是这个函数的图象的最高点,也就是说,当取顶点的横坐标时,这个函数有最大值。
因此,当时,有最大值也就是说,小球运动的时间是时,小球最高。小球运动中的最大高度是。
22.3
实际问题与二次函数
一般地,当时,抛物线的顶点是最(高)点,也就是说,当时,二次函数有最小(大)值。
我们再来解决一些实际问题。
22.3
实际问题与二次函数
例9:用总长为
的篱笆围成矩形场地,矩形面积
随矩形一边长
的变化而变化。当
是多少米时,场地的面积
最大?
[解析]
先写出
关于
的函数解析式,再求出使
最大的
的值。
矩形场地的周长是,一边长为
,所以另一边长为。场地的面积,即
因此,当
时,
有最大值也就是说,当
是
时,场地的面积
最大。
22.3
实际问题与二次函数
例10:某商品现在的售价为每件
60
元,每星期可卖出
300
件市场调查反映:如调整价格,每涨价
1
元,每星期要少卖出
10
件;每降价
1
元,每星期可多卖出
20
件。已知商品的进价为每件
40
元,如何定价才能使利润最大?
[解析]
调整价格包括涨价和降价两种情况,先看涨价的情况:设每涨价
元,每星期售出商品的利润为
元。涨价
元时,每星期少卖
件,实际卖出
件,销售额为
元,买进商品需支付
元。因此,所得利润
即
当
时,
最大,也就是说,涨价的情况下,涨价
5
元,即定价
65
元时,利润最大,最大利润为
6250
元。
22.3
实际问题与二次函数
例10:某商品现在的售价为每件
60
元,每星期可卖出
300
件市场调查反映:如调整价格,每涨价
1
元,每星期要少卖出
10
件;每降价
1
元,每星期可多卖出
20
件。已知商品的进价为每件
40
元,如何定价才能使利润最大?
[解析]
再看降价的情况:设每降价
元,每星期售出商品的利润为
元。降价
元时,每星期多卖
件,实际卖出
件,销售额为
元,买进商品需支付
元。因此,所得利润
即
当
时,
最大,也就是说,降价的情况下,降价
2.5
元,即定价
57.5
元时,利润最大,最大利润为
6125
元。
22.3
实际问题与二次函数
例11:某种商品每件的进价为元,在某段时间内若以每件工元出售,可卖出
件,应如何定价才能使利润最大?
例12:飞机着陆后滑行的距离
(单位:)
关于滑行的时间
(单位:)
的函数解析式是,飞机着陆后滑行多远才能停下来?
例13:已知直角三角形两条直角边的和等于,两条直角边各为多少时,这个直角三角形的面积最大?最大值是多少?
总结
二次函数:形如的函数。
抛物线
的特点
开口方向:当,开口向上;当时,开口向下
对称轴:
顶点:
增减性:
1、若,当时,
随增大而减小,当时,
随增大而增大;
2、若,当时,
随增大而增大,当时,
随增大而减小。
二次函数与一元二次方程:
由二次函数图象与?轴位置关系的情况,可以得出相应一元二次方程的根;
反过来,由一元二次方程的根的情况,也可以确定相应二次函数图象与轴的位置关系。
二次函数解决实际问题:
一般地,当时,抛物线的顶点是最(高)点,也就是说,当时,二次函数有最小(大)值。
第
22
章
二次函数
Quadratic
Function
回顾:正比例函数和一次函数
我们学过哪些函数?
一次函数
形如
与轴的交点坐标为,与轴的交点坐标为
当时,
随的增大而增大;
当时,
随的增大而减小;
当时,函数图像与轴交于正半轴;
当时,函数图像与轴交于负半轴;
当时,函数图像过原点,是个正比例函数。
解析式的确定:待定系数法(设、代、解,得,验)
平移:上加下减、左加右减
引入:
个球队参加比赛,每两队之间进行一场比赛。比赛的场次数与球队数有什么关系?
每个队要与其他个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛是同一场比赛
所以比赛的场次数
即
像上式这样,比赛的场次数与球队数的关系,对于的每一个值,
都有一个对应值,那么我们说,是的函数。
22.1
二次函数的图像和性质
22.1
二次函数的图像和性质
定义:形如的函数。其中,是自变量,
分别是函数解析式的二次项系数、一次项系数和常数项。
注意:每项的系数包括它前面的符号
那么,这个函数的图像是怎么样的呢?
跟其他函数一样,我们可以通过「描点法」来粗略地画出二次函数的图像。以为例:
22.1
二次函数的图像和性质
-3
-2
-1
0
1
2
3
9
4
1
0
1
4
9
22.1
二次函数的图像和性质
我们描出上述点,再用平滑的曲线连接这些点后,不难发现,二次函数的图象是一条曲线,它的形状类似于投篮时或掷铅球时球在空中所经过的路线,只是这条曲线开口向上。这条曲线叫做抛物线。
实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下。
22.1
二次函数的图像和性质
还可以看出,轴是抛物线的对称轴,抛物线与它的对称轴的交点(0,0)叫做抛物线的顶点,它是抛物线的最低点。实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的顶点。顶点是抛物线的最低点或最高点。
22.1
二次函数的图像和性质
从二次函数的图象可以看出:在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛物线从左到右上升。
也就是说,当时,
随的增大而减小;当时,
随的增大而增大。
22.1
二次函数的图像和性质
我们已经知道的图象,那么的图像与有何异同呢?
一般地,当时,抛物线的开口向上,对称轴是轴,顶点是原点,顶点是抛物线的最低点,
越大,抛物线的开口越小。类似地,我们可以研究当时,二次函数的图象和性质.
22.1
二次函数的图像和性质
一般地,当时,抛物线的开口向下,对称轴是轴,顶点是原点,顶点是抛物线的最低点,
越大,抛物线的开口越小。
22.1
二次函数的图像和性质
的图像我们已经了解了,在之前学习其他函数的时候,我们学习了函数的平移:「上加下减,左加右减」,这个口诀对二次函数一样适用。
首先我们先来对他进行上下平移,试着用描点法画出和的图像。
可以看出,把向上平移个单位长度,就得到抛物线;把抛物线向下平移个单位长度,就得到抛物线。
22.1
二次函数的图像和性质
,对它进行左右平移呢?
试着画出和的图像。
可以看出,把向左平移个单位长度,就得到;把向右平移个单位长度,就得到抛物线。
他们的开口都向下,其中的对称轴是,顶点是;
的对称轴是,顶点是。
22.1
二次函数的图像和性质
归纳:通过上面的几种变形我们发现,
与的形状相同,但是位置不同,把进行平移后,就可以得到抛物线
。
抛物线
有如下特点
开口方向:当,开口向上;当时,开口向下
对称轴:
顶点:
增减性:
1、若,当时,
随增大而减小,当时,
随增大而增大;
2、若,当时,
随增大而增大,当时,
随增大而减小。
22.1
二次函数的图像和性质
例1:要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
[解析]
如图,以水管与地面交点为原点,原点与水柱落地处所在直线为轴,水管所在直线为轴,建立直角坐标系。
点是图中这段抛物线的顶点,因此可设这段抛物线对应的函数解析式是
∵抛物线经过点,可得
解得
因此
当时,
也就是说,水管应2.25m长。
22.1
二次函数的图像和性质
我们知道,二次函数解析式中一般式是,刚刚研究的都是顶点式:的函数图像,那么他们之间有什么联系呢?
事实上,我们可以把通过配方法化成的形式,即
因此,抛物线的对称轴是,顶点是。
22.1
二次函数的图像和性质
如图所示,从二次函数的图像可以看出:
若,当时,
随增大而减小,当时,
随增大而增大;
若,当时,
随增大而增大,当时,
随增大而减小。
22.1
二次函数的图像和性质
二次函数解析式归纳:
一般式:
顶点式:
22.1
二次函数的图像和性质
例2:分别写出抛物线与的开口方向、对称轴和顶点。
[答案]
开口方向
对称轴
顶点
向上
或轴
向下
或轴
22.1
二次函数的图像和性质
例3:分别写出抛物线、、
的开口方向、对称轴和顶点。
[答案]
开口方向
对称轴
顶点
向上
或轴
向下
向上
22.1
二次函数的图像和性质
我们之前学过一次函数解析式的确定,已知两点就可以确定一条直线的解析式。那么,二次函数的解析式该如何确定呢?
确定一次函数,即写出这个一次函数的解析式,需求出,的值。用待定系数法,由两点(两点的连线不与坐标轴平行)的坐标,列出关于,的二元一次方程组就可以求出的值。
类似地,确定二次函数,即写出这个二次函数的解析式,需求出的值。由不共线三点(三点不在同一直线上)的坐标,列出关于的三元一次方程组就可以求出的值。
22.1
二次函数的图像和性质
例4:已知抛物线过三点,求该抛物线的函数解析式。
[解析]
因为抛物线过三点,所以可以得到关于阿的三元一次方程组:
解这个方程组,得
所求二次函数是
22.1
二次函数的图像和性质
思考:是不是一条抛物线至少需要三个点才能确定他的解析式呢?
我们知道二次函数解析式的一般式是,他有三个参数,就需要三个方程才能求解。
但是对于他的顶点式
来说,顶点坐标是,那么当我们知道顶点坐标时,顶点式中就只剩一个参数是未知的了,此时只需要抛物线上除顶点外的一点就可以求出它的解析式。
22.1
二次函数的图像和性质
例5:已知抛物线上两点,其中点是该抛物线的顶点,求该抛物线的函数解析式。
[解析]
∵抛物线的顶点坐标为
∴设抛物线解析式为
把点
代入中
得
解得
∴该抛物线的函数解析式为
22.2
二次函数与一元二次方程
22.2
二次函数与一元二次方程
例6:如右下图所示,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度
h(单位:m)与飞行时间(单位:s)之间具有函数关系
(1)小球的飞行高度能否达到15m?如果能,需要多少飞行时间?
解:依题得
即
解得
,
∴当小球飞行1s和3s时,它的飞行高度为15m。
22.2
二次函数与一元二次方程
例6:如右下图所示,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度
h(单位:m)与飞行时间(单位:s)之间具有函数关系
(2)小球的飞行高度能否达到20m?如果能,需要多少飞行时间?
解:依题得
即
解得
∴当小球飞行2s时,它的飞行高度为20m。
22.2
二次函数与一元二次方程
例6:如右下图所示,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度
h(单位:m)与飞行时间(单位:s)之间具有函数关系
(3)小球的飞行高度能否达到20.5m?为什么?
解:依题得
即
因为
∴方程无实数根,即小球的飞行高度达不到20.5m。
22.2
二次函数与一元二次方程
例6:如右下图所示,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线。如果不考虑空气阻力,小球的飞行高度
h(单位:m)与飞行时间(单位:s)之间具有函数关系
(4)小球从飞出到落地要用多少时间?
解:小球飞出及落地时的高度都为0m,
即
即
解得
,
∴小球在0s时起飞,在4s时落地,从飞出到落地要用4s。
22.2
二次函数与一元二次方程
从上面可以看出,二次函数与一元二次方程联系密切。例如,已知二次函数的值为,求自变量的值,可以看作解一元二次方程(即)。反过来,解方程又可以看作已知二次函数的值为,求自变量的值。
一般地,我们可以利用二次函数深入讨论一元二次方程
。
22.2
二次函数与一元二次方程
例7:下列二次函数的图象与轴有公共点吗?如果有,公共点的横坐标是多少?当取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
这些函数的图像如右下图所示。
(1)
(2)
(3)
[解析]
抛物线与轴有两个公共点
它们的横坐标是
当取公共点的横坐标时,函数值是
由此得出方程的根是
22.2
二次函数与一元二次方程
例7:下列二次函数的图象与轴有公共点吗?如果有,公共点的横坐标是多少?当取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
这些函数的图像如右下图所示。
(1)
(2)
(3)
[解析]
抛物线与轴有一个公共点
这点的横坐标是
当时,函数值是
由此得出方程有两个相等的实数根
22.2
二次函数与一元二次方程
例7:下列二次函数的图象与轴有公共点吗?如果有,公共点的横坐标是多少?当取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
这些函数的图像如右下图所示。
(1)
(2)
(3)
[解析]
抛物线与工轴没有公共点
由此可知,方程没有实数根
22.2
二次函数与一元二次方程
例7:下列二次函数的图象与轴有公共点吗?如果有,公共点的横坐标是多少?当取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
这些函数的图像如右下图所示。
(1)
(2)
(3)
[归纳]
由二次函数图象与?轴位置关系的情况,可以得出相应一元二次方程的根;
反过来,由一元二次方程的根的情况,也可以确定相应二次函数图象与轴的位置关系。
22.3
实际问题与二次函数
22.3
实际问题与二次函数
对于某些实际问题,如果其中变量之间的关系可以用二次函数模型来刻画,那么我们就可以利用二次函数的图象和性质来研究。
例8:从地面竖直向上抛出一小球,小球的高度(单位:)与小球的运动时间(单位:)之间的关系式是小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是这个函数的图象的最高点,也就是说,当取顶点的横坐标时,这个函数有最大值。
因此,当时,有最大值也就是说,小球运动的时间是时,小球最高。小球运动中的最大高度是。
22.3
实际问题与二次函数
一般地,当时,抛物线的顶点是最(高)点,也就是说,当时,二次函数有最小(大)值。
我们再来解决一些实际问题。
22.3
实际问题与二次函数
例9:用总长为
的篱笆围成矩形场地,矩形面积
随矩形一边长
的变化而变化。当
是多少米时,场地的面积
最大?
[解析]
先写出
关于
的函数解析式,再求出使
最大的
的值。
矩形场地的周长是,一边长为
,所以另一边长为。场地的面积,即
因此,当
时,
有最大值也就是说,当
是
时,场地的面积
最大。
22.3
实际问题与二次函数
例10:某商品现在的售价为每件
60
元,每星期可卖出
300
件市场调查反映:如调整价格,每涨价
1
元,每星期要少卖出
10
件;每降价
1
元,每星期可多卖出
20
件。已知商品的进价为每件
40
元,如何定价才能使利润最大?
[解析]
调整价格包括涨价和降价两种情况,先看涨价的情况:设每涨价
元,每星期售出商品的利润为
元。涨价
元时,每星期少卖
件,实际卖出
件,销售额为
元,买进商品需支付
元。因此,所得利润
即
当
时,
最大,也就是说,涨价的情况下,涨价
5
元,即定价
65
元时,利润最大,最大利润为
6250
元。
22.3
实际问题与二次函数
例10:某商品现在的售价为每件
60
元,每星期可卖出
300
件市场调查反映:如调整价格,每涨价
1
元,每星期要少卖出
10
件;每降价
1
元,每星期可多卖出
20
件。已知商品的进价为每件
40
元,如何定价才能使利润最大?
[解析]
再看降价的情况:设每降价
元,每星期售出商品的利润为
元。降价
元时,每星期多卖
件,实际卖出
件,销售额为
元,买进商品需支付
元。因此,所得利润
即
当
时,
最大,也就是说,降价的情况下,降价
2.5
元,即定价
57.5
元时,利润最大,最大利润为
6125
元。
22.3
实际问题与二次函数
例11:某种商品每件的进价为元,在某段时间内若以每件工元出售,可卖出
件,应如何定价才能使利润最大?
例12:飞机着陆后滑行的距离
(单位:)
关于滑行的时间
(单位:)
的函数解析式是,飞机着陆后滑行多远才能停下来?
例13:已知直角三角形两条直角边的和等于,两条直角边各为多少时,这个直角三角形的面积最大?最大值是多少?
总结
二次函数:形如的函数。
抛物线
的特点
开口方向:当,开口向上;当时,开口向下
对称轴:
顶点:
增减性:
1、若,当时,
随增大而减小,当时,
随增大而增大;
2、若,当时,
随增大而增大,当时,
随增大而减小。
二次函数与一元二次方程:
由二次函数图象与?轴位置关系的情况,可以得出相应一元二次方程的根;
反过来,由一元二次方程的根的情况,也可以确定相应二次函数图象与轴的位置关系。
二次函数解决实际问题:
一般地,当时,抛物线的顶点是最(高)点,也就是说,当时,二次函数有最小(大)值。
同课章节目录
