2021-2022学年人教版数学八年级上册12.2 .2全等三角形的判定 “边角边” 课件(17张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册12.2 .2全等三角形的判定 “边角边” 课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 21:04:49 | ||
图片预览




文档简介
(共17张PPT)
12.2三角形全等的
判定
第2课时
“边角边”
教学目标
1.三角形全等的“边角边”的条件.
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3.掌握三角形全等的“SAS”条件.
4.能运用“SAS”证明简单的三角形全等问题.
新课导入
还记得作一个角等于已知角的方法吗?
4
做一做:先任意画出△ABC.再画一个△A′B′C′,
使A′B′=AB,
A′C′=AC,∠A′=∠A.(即有两边和它们
的夹角相等).把画好的△A′B′C′剪下,放到△ABC上,
它们全等吗?
画法:
2.
在射线A′M上截取A′B′=AB
3.
在射线A′N上截取A′C′=AC
1.
画∠MA′N=∠A
4.
连接B′C′
∴△A′B′C′就是所求的三角形.
5
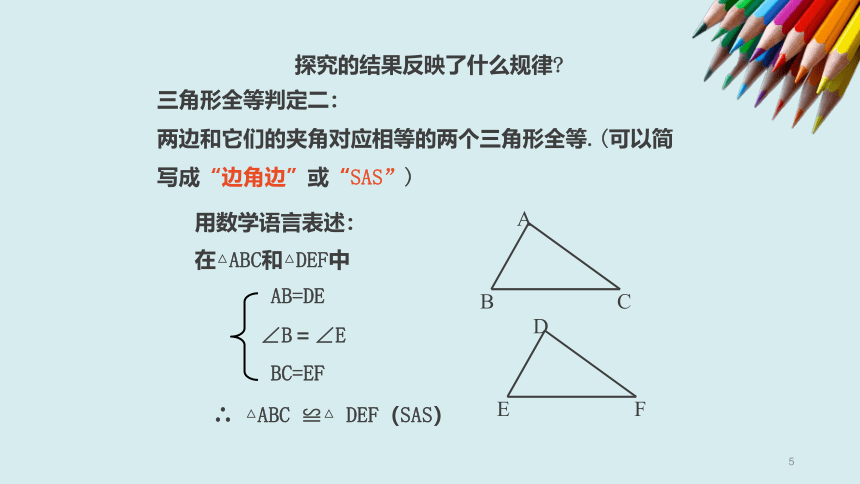
三角形全等判定二:
两边和它们的夹角对应相等的两个三角形全等.(可以简
写成“边角边”或“SAS”)
用数学语言表述:
A
B
C
D
E
F
在△ABC和△DEF中
∴
△ABC
≌△
DEF(SAS)
AB=DE
∠B=∠E
BC=EF
探究的结果反映了什么规律?
6
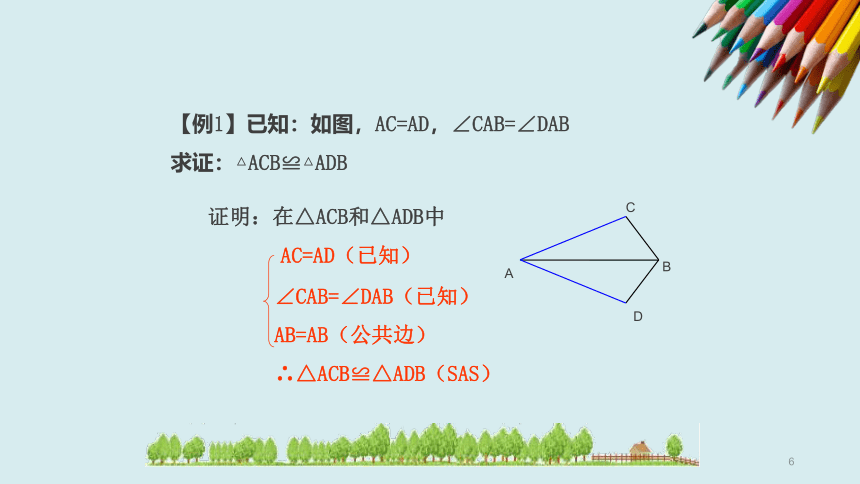
【例1】已知:如图,AC=AD,∠CAB=∠DAB
求证:△ACB≌△ADB
AC=AD(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴△ACB≌△ADB(SAS)
证明:在△ACB和△ADB中
A
B
C
D
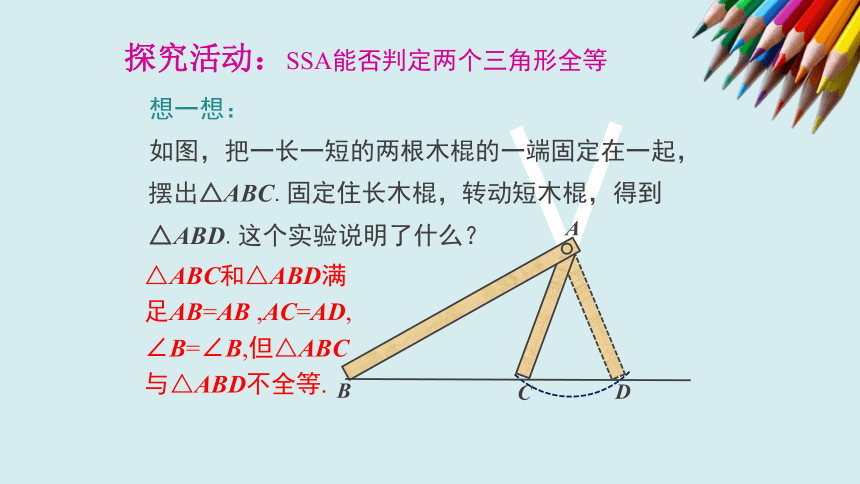
想一想:
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB
,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
探究活动:SSA能否判定两个三角形全等
画一画:
画△ABC
和△DEF,使∠B
=∠E
=30°,
AB
=DE
=5
cm
,AC
=DF
=3
cm
.观察所得的两个三角形是否全等?
?
A
B
M
C
D
A
B
C
A
B
D
有两边和其中一边的对角分别相等的两个三角形不一定全等.
结论
9
已知:AD=CD,BD平分∠ADC
求证:(1)∠A=∠C
(2)AB=BC
A
B
C
D
1
2
归纳:证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到.
分析:可先证△ABD≌△CBD(SAS)
再根据全等三角形的性质证角或线段相等.
例
下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
C
方法总结:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
典例精析
1.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是
(
)
A.∠A=∠D
B.∠E=∠C
C.∠A=∠C
D.∠ABD=∠EBC
?
D
课后练习
12
2.已知:如图,AD∥BC,AD=CB,
求证:△ADC≌△CBA
AD=CB(已知)
∠1=∠2(已知)
AC=CA
(公共边)
∴△ADC≌△CBA(SAS)
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中
D
C
1
A
2
B
13
3.根据题中条件,分别找出各题中的全等三角形.
A
B
C
40°
D
E
F
(1)
(1)△ABC≌△EFD
根据“SAS”
(2)△ADC≌△CBA
根据“SAS”
40°
D
C
A
B
(2)
14
4.如图,点A、E、B、D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?并说明理由.
_
F
_
E
_
B
_
A
_
C
_
D
5.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF.
求证:△AFD≌△CEB.
F
A
B
D
C
E
证明:
∵AD//BC,
∴
∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
AD=CB
∠A=∠C
AF=CE
∴△AFD≌△CEB(SAS).
∴AE+EF=CF+EF,
即
AF=CE.
(已知),
(已证),
(已证),
6.已知:如图,AB=AC,AD是△ABC的角平分线,
求证:BD=CD.
证明:
∵AD是△ABC的角平分线,
∴
∠BAD=∠CAD,
在△ABD和△ACD中,
AB=AC
∠BAD=∠CAD
AD=AD
∴△ABD≌△ACD(SAS).
(已知),
(已证),
(已证),
∴
BD=CD.
课堂小结
1.根据边角边定理判定两个三角形全等,要找出两边
及夹角对应相等的三个条件.
2.找使结论成立所需条件,要充分利用已知条件
(包括给出图形中的隐含条件,如公共边、公共角等),
并要善于运用学过的定义、公理、定理.
12.2三角形全等的
判定
第2课时
“边角边”
教学目标
1.三角形全等的“边角边”的条件.
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3.掌握三角形全等的“SAS”条件.
4.能运用“SAS”证明简单的三角形全等问题.
新课导入
还记得作一个角等于已知角的方法吗?
4
做一做:先任意画出△ABC.再画一个△A′B′C′,
使A′B′=AB,
A′C′=AC,∠A′=∠A.(即有两边和它们
的夹角相等).把画好的△A′B′C′剪下,放到△ABC上,
它们全等吗?
画法:
2.
在射线A′M上截取A′B′=AB
3.
在射线A′N上截取A′C′=AC
1.
画∠MA′N=∠A
4.
连接B′C′
∴△A′B′C′就是所求的三角形.
5
三角形全等判定二:
两边和它们的夹角对应相等的两个三角形全等.(可以简
写成“边角边”或“SAS”)
用数学语言表述:
A
B
C
D
E
F
在△ABC和△DEF中
∴
△ABC
≌△
DEF(SAS)
AB=DE
∠B=∠E
BC=EF
探究的结果反映了什么规律?
6
【例1】已知:如图,AC=AD,∠CAB=∠DAB
求证:△ACB≌△ADB
AC=AD(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴△ACB≌△ADB(SAS)
证明:在△ACB和△ADB中
A
B
C
D
想一想:
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB
,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
探究活动:SSA能否判定两个三角形全等
画一画:
画△ABC
和△DEF,使∠B
=∠E
=30°,
AB
=DE
=5
cm
,AC
=DF
=3
cm
.观察所得的两个三角形是否全等?
?
A
B
M
C
D
A
B
C
A
B
D
有两边和其中一边的对角分别相等的两个三角形不一定全等.
结论
9
已知:AD=CD,BD平分∠ADC
求证:(1)∠A=∠C
(2)AB=BC
A
B
C
D
1
2
归纳:证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到.
分析:可先证△ABD≌△CBD(SAS)
再根据全等三角形的性质证角或线段相等.
例
下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
C
方法总结:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
典例精析
1.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是
(
)
A.∠A=∠D
B.∠E=∠C
C.∠A=∠C
D.∠ABD=∠EBC
?
D
课后练习
12
2.已知:如图,AD∥BC,AD=CB,
求证:△ADC≌△CBA
AD=CB(已知)
∠1=∠2(已知)
AC=CA
(公共边)
∴△ADC≌△CBA(SAS)
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中
D
C
1
A
2
B
13
3.根据题中条件,分别找出各题中的全等三角形.
A
B
C
40°
D
E
F
(1)
(1)△ABC≌△EFD
根据“SAS”
(2)△ADC≌△CBA
根据“SAS”
40°
D
C
A
B
(2)
14
4.如图,点A、E、B、D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?并说明理由.
_
F
_
E
_
B
_
A
_
C
_
D
5.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF.
求证:△AFD≌△CEB.
F
A
B
D
C
E
证明:
∵AD//BC,
∴
∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
AD=CB
∠A=∠C
AF=CE
∴△AFD≌△CEB(SAS).
∴AE+EF=CF+EF,
即
AF=CE.
(已知),
(已证),
(已证),
6.已知:如图,AB=AC,AD是△ABC的角平分线,
求证:BD=CD.
证明:
∵AD是△ABC的角平分线,
∴
∠BAD=∠CAD,
在△ABD和△ACD中,
AB=AC
∠BAD=∠CAD
AD=AD
∴△ABD≌△ACD(SAS).
(已知),
(已证),
(已证),
∴
BD=CD.
课堂小结
1.根据边角边定理判定两个三角形全等,要找出两边
及夹角对应相等的三个条件.
2.找使结论成立所需条件,要充分利用已知条件
(包括给出图形中的隐含条件,如公共边、公共角等),
并要善于运用学过的定义、公理、定理.
