第1章 全等三角形 章末测试2021-2022学年苏科版数学八年级上册(word版含答案)
文档属性
| 名称 | 第1章 全等三角形 章末测试2021-2022学年苏科版数学八年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 754.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 11:14:29 | ||
图片预览



文档简介
第一章
全等三角形
章末测试
一、单选题(每小题3分,共36分)
1.下列各组的两个图形属于全等图形的是(
)
A.B.
C.
D.
2.下面说法一定正确的有(
)
①全等图形的形状和大小都相同
②全等三角形的对应角相等
③全等三角形的高相等
④全等三角形的对应边相等
A.1个
B.2个
C.3个
D.4个
3.如图,在中,D,E分别是边,上的点,若,则的度数为(
)
A.
B.
C.
D.
4.如图,,,、分别为线段和射线上的一点,若点从点出发向点运动,同时点从点出发向点运动,二者速度之比为,运动到某时刻同时停止,在射线上取一点,使与全等,则的长为(
)
A.2
B.3
C.2或3
D.2或6
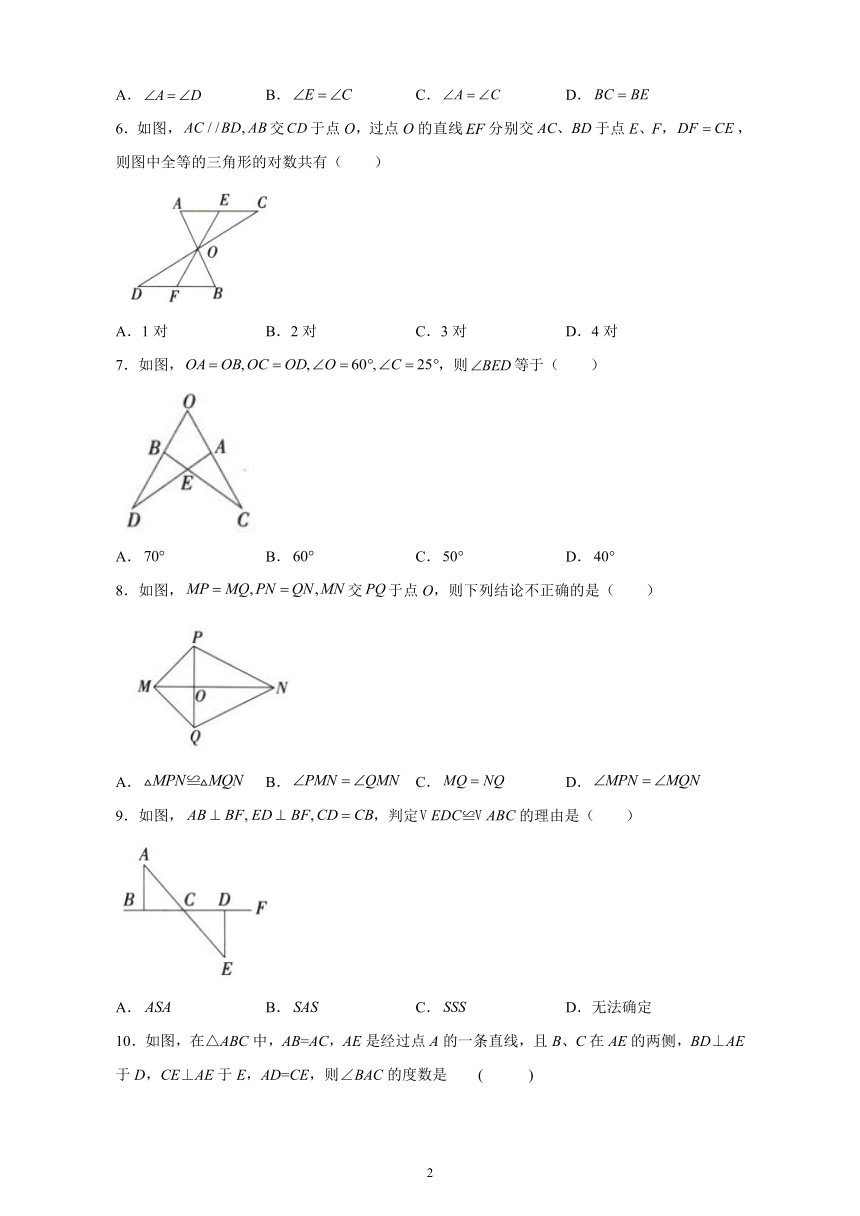
5.如图,,欲证,则补充的条件中不正确的是(
)
A.
B.
C.
D.
6.如图,交于点O,过点O的直线分别交于点E、F,,则图中全等的三角形的对数共有(
)
A.1对
B.2对
C.3对
D.4对
7.如图,,则等于(
)
A.
B.
C.
D.
8.如图,交于点O,则下列结论不正确的是(
)
A.
B.
C.
D.
9.如图,,判定的理由是(
)
A.
B.
C.
D.无法确定
10.如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是
(
)
A.45°
B.60°
C.90°
D.120°
11.如图,某同学把一块三角形的玻璃打碎成3块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是______,这么做的依据是______.(
)
A.带①去,
B.带②去,
C.带③去,
D.①②③都带去,
12.如图,的面积为14,平分,且于点,则的面积是(
)
A.5
B.7
C.9
D.11
二、填空题(每小题3分,共24分)
13.如图,由4个相同的小正方形组成的格点图中,∠1+∠2+∠3=________度.
14.如图,,且,则______度.
15.如图,AD=BC,若利用“SSS”来证明△ABD≌△CDB,则需要添加的一个条件是__________.
16.两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接.一只蜗牛在爬行速度不变的情况下,从C爬到D所用的最短时间与它爬行线段__________所用的时间相同.(不要使用图形中未标注的字母)
17.数学课上,同学们探讨利用不同画图工具画角的平分线的方法.小旭说:我用两块含的直角三角板就可以画角平分线.如图,取,把直角三角板按如图所示的位置放置,两直角边交于点P,则射线OP是的平分线.小旭这样画的理论依据是______.
18.如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.小明测得C、D间的距离为90米,则在A点处小明与游艇的距离为______米.
19.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,要测量工件内槽宽AB,只要测量A'B'的长度即可,该做法的依据是
___.
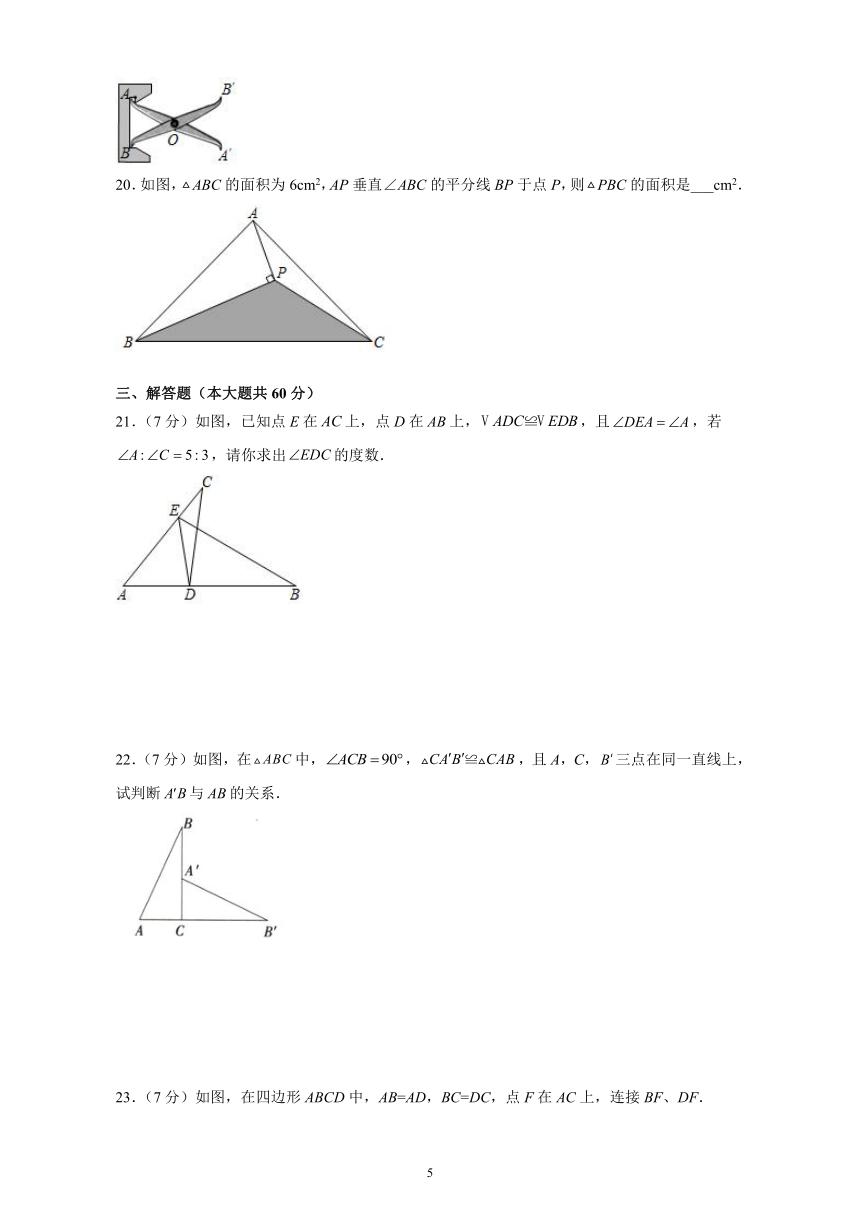
20.如图,ABC的面积为6cm2,AP垂直∠ABC的平分线BP于点P,则PBC的面积是___cm2.
三、解答题(本大题共60分)
21.(7分)如图,已知点E在上,点D在上,,且,若,请你求出的度数.
22.(7分)如图,在中,,,且A,C,三点在同一直线上,试判断与的关系.
23.(7分)如图,在四边形ABCD中,AB=AD,BC=DC,点F在AC上,连接BF、DF.
求证:BF=DF.
24.(9分)如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE.
(1)求证△ADB≌△AEC;
(2)DB⊥EC.
25.(9分)十九中趣味数学社的同学用10块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合.
(1)求证:;
(2)求两堵木墙之间的距离.
26.(9分)如图,在中,为延长线上一点,点在上,且.
(1)求证:;
(2)若,求的度数.
27.(12分)在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连接EF.
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为______.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.
参考答案
1.D
解:A、两个图形不能完全重合,不是全等图形,不符合题意,
B.两个图形不能完全重合,不是全等图形,符合题意,
C.两个图形不能完全重合,不是全等图形,不符合题意,
D.两个图形能完全重合,是全等图形,不符合题意,
故选D.
2.C
解:①全等图形的形状和大小都相同,故此说法正确;
②全等三角形的对应角相等,故此说法正确;
③全等三角形的对应边的高相等,故此说法错误;
④全等三角形的对应边相等,故此说法正确.
故选C.
3.D
解:∵,∠DEB+∠DEC=180°,
∴,
又∵,
∴
∴,
即
故选:D.
4.D
解:设BE=t,则BF=2t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
情况一:当BE=AG,BF=AE时,
∵BF=AE,AB=6,
∴2t=6-t,
解得:t=2,
∴AG=BE=2;
情况二:当BE=AE,BF=AG时,
∵BE=AE,AB=6,
∴t=6-t,
解得:t=3,
∴AG=BF=2t=6,
综上所述,AG=2或AG=6.
故选D.
5.C
解:∵,
∴,
∴,∵,
在和中,
∴,故A正确;
∵,
在和中,
∴,故B正确;
∵,
在和中,
∴,故D正确;
C中条件不能证明.
6.C
解:,
同理可得:
全等三角形有△AEO≌△BFO,△CEO≌△DFO,△ACO≌△BDO,共3对,
故选:C.
7.A
解:在△ODA和△OCB中
∴△ODA≌△OCB(SAS),
∴∠D=∠C=25°,
∵∠O=60°,∠C=25°,
∴∠DBE=60°+25°=85°,
∴∠BED=180°?85°?25°=70°,
故选:A.
8.C
解:A、因为,所以,选项正确;
B、因为,所以正确;
C、由,可以得到,选项错误;
D、由,可得,选项正确.
故选:C
9.A
解:∵,
∴,
∵和为对顶角,
∴,
又∵,
∴.
故选:A.
10.C
解:∵BD⊥AE于D,CE⊥AE于E,
∴∠ADB=∠E=90,
在Rt△BAD和Rt△ACE中,
AB=AC、
AD=EC
∴△BAD≌△CAE(HL),
∴∠BAD=∠ACE,
∵∠ACE+∠CAE=90°,
∴∠BAC
=∠BAD+∠CAE=90°.
故选C.
11.C
解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故选:C.
12.B
解:延长BD交AC于点E,
∵平分,
∴,
∵,
∴,
∵AD=AD,
∴△ADB≌△ADE,
∴BD=ED,,
∴,
∴,
∴,
故选:B.
13.135
解:如图所示,
在△ACB和△DCE中,
,
∴,
∴,
∴;
故答案是:.
14.
解:∵△ABC≌△ADE,∠EAB=112°,
∴∠EAD=DAB=56°,∠D=∠B,
∴∠ACB+∠B=180°-56°=124°,
∵∠ACB=∠FCD,
∴∠FCD+∠D=124°,
∵∠EFC是△FCD的一个外角,
∴∠EFC=∠FCD+∠D=124°,
故答案为:124.
15.
解:∵AD=BC,BD=DB,
∴当添加AB=CD时,可根据“SSS”判断△ABD≌△CDB.
故答案为:AB=CD.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
16.
解:∵和是等腰直角三角形,
∴,
∴,
∴,
在和中,,
∴≌(SAS),
∴.
故答案为:BE.
17.HL
解:∵∠OMP=∠ONP=90°,且OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP是∠AOB的平分线.
故答案为:HL.
18.90
解:在△ABS与△CBD中,
∵,
∴△ABS≌△CBD(ASA),
∴AS=CD=90(米).
故答案是:90.
19.根据证明.
解:连接,,如图,
点分别是、的中点,
,,
在和中,
,
∴.
.
答:需要测量的长度,即为工件内槽宽.
其依据是根据证明;
故答案为:根据证明.
20.3
解:延长AP交BC于点E,如图所示.
∵AP垂直∠ABC的平分线BP于点P,
∴∠ABP=∠EBP.
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=EP.
∵△APC和△EPC等底同高,
∴S△APC=S△CPE,
∴S△PBC=S△BPE+S△CPE=S△ABC=×6=3(cm2),
故答案为:3.
21.20°
解:设,,
则,
,
∵,
∴,
∴,
∴,
∴,
∴,
解得,
∴.
22.与互相垂直且相等.证明见解析
解:与互相垂直且相等.
如图,延长交于点M.
∵,∠ACB=90°
,
∴,,
∵,
∴,
∴,
∴与互相垂直且相等.
23.见解析
解:证明:在△ABC和△ADC中,
∵,
∴△ABC≌△ADC(SSS),
∴∠BCF=∠DCF,
在△BCF和△DCF中,
∵,
∴△BCF≌△DCF(SAS),
∴BF=DF.
24.(1)见详解;(2)见详解
解:(1)证明:∵AB⊥AC,AD⊥AE,
∴∠BAC=∠DAE=90°,
∴∠BAC+∠BAE=∠DAE+∠BAE,
∴∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△ADB≌△AEC(SAS);
(2)由(1)知,△ADB≌△AEC,
∴∠ACE=∠ABD,
∵∠BAC=90°,
∴∠CBD+∠BCE=∠ABC+∠ACB=90°,
∴∠BFC=90°,
∴DB⊥EC.
25.(1)见详解;(2)
解:(1)证明:由题意得:,,
∴,
∴,
∴
在和中
,
∴;
(2)解:由题意得:,
∵,
∴,
∴,
答:两堵木墙之间的距离为.
26.(1)见解析;(2)
解:(1)证明:,
,
在和中,
,
;
(2),,
,
又∵,,
,
,
,
,
,
即.
27.猜想:DE=DF;探究:DE=DF,证明见解析;应用:S△DEF=8.
解:猜想:DE=DF.
如图1,连接CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为边AB的中点,
∴CD=AD,∠BCD=∠ACB=45°,
∴∠EAD=∠FCD,
在△AED和△CFD中,,
∴△ADE≌△CDF(SAS),
∴DE=DF,
故答案为:DE=DF;
探究:DE=DF,证明如下:
如图2,连接CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为AB中点,
∴AD=CD,∠BCD=∠ACB=45°,
∵∠CAD+∠EAD=∠BCD+∠FCD=180°,
∴∠EAD=∠FCD=135°,
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS),
∴DE=DF;
应用:
∵△ADE≌△CDF,
∴∠ADE=∠CDF,
∵∠ADC=90°,
∴∠EDF=90°,
∵DE=DF=4,
∴S△DEF=DE2=×42=8.
全等三角形
章末测试
一、单选题(每小题3分,共36分)
1.下列各组的两个图形属于全等图形的是(
)
A.B.
C.
D.
2.下面说法一定正确的有(
)
①全等图形的形状和大小都相同
②全等三角形的对应角相等
③全等三角形的高相等
④全等三角形的对应边相等
A.1个
B.2个
C.3个
D.4个
3.如图,在中,D,E分别是边,上的点,若,则的度数为(
)
A.
B.
C.
D.
4.如图,,,、分别为线段和射线上的一点,若点从点出发向点运动,同时点从点出发向点运动,二者速度之比为,运动到某时刻同时停止,在射线上取一点,使与全等,则的长为(
)
A.2
B.3
C.2或3
D.2或6
5.如图,,欲证,则补充的条件中不正确的是(
)
A.
B.
C.
D.
6.如图,交于点O,过点O的直线分别交于点E、F,,则图中全等的三角形的对数共有(
)
A.1对
B.2对
C.3对
D.4对
7.如图,,则等于(
)
A.
B.
C.
D.
8.如图,交于点O,则下列结论不正确的是(
)
A.
B.
C.
D.
9.如图,,判定的理由是(
)
A.
B.
C.
D.无法确定
10.如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是
(
)
A.45°
B.60°
C.90°
D.120°
11.如图,某同学把一块三角形的玻璃打碎成3块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是______,这么做的依据是______.(
)
A.带①去,
B.带②去,
C.带③去,
D.①②③都带去,
12.如图,的面积为14,平分,且于点,则的面积是(
)
A.5
B.7
C.9
D.11
二、填空题(每小题3分,共24分)
13.如图,由4个相同的小正方形组成的格点图中,∠1+∠2+∠3=________度.
14.如图,,且,则______度.
15.如图,AD=BC,若利用“SSS”来证明△ABD≌△CDB,则需要添加的一个条件是__________.
16.两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接.一只蜗牛在爬行速度不变的情况下,从C爬到D所用的最短时间与它爬行线段__________所用的时间相同.(不要使用图形中未标注的字母)
17.数学课上,同学们探讨利用不同画图工具画角的平分线的方法.小旭说:我用两块含的直角三角板就可以画角平分线.如图,取,把直角三角板按如图所示的位置放置,两直角边交于点P,则射线OP是的平分线.小旭这样画的理论依据是______.
18.如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.小明测得C、D间的距离为90米,则在A点处小明与游艇的距离为______米.
19.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,要测量工件内槽宽AB,只要测量A'B'的长度即可,该做法的依据是
___.
20.如图,ABC的面积为6cm2,AP垂直∠ABC的平分线BP于点P,则PBC的面积是___cm2.
三、解答题(本大题共60分)
21.(7分)如图,已知点E在上,点D在上,,且,若,请你求出的度数.
22.(7分)如图,在中,,,且A,C,三点在同一直线上,试判断与的关系.
23.(7分)如图,在四边形ABCD中,AB=AD,BC=DC,点F在AC上,连接BF、DF.
求证:BF=DF.
24.(9分)如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE.
(1)求证△ADB≌△AEC;
(2)DB⊥EC.
25.(9分)十九中趣味数学社的同学用10块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合.
(1)求证:;
(2)求两堵木墙之间的距离.
26.(9分)如图,在中,为延长线上一点,点在上,且.
(1)求证:;
(2)若,求的度数.
27.(12分)在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连接EF.
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为______.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.
参考答案
1.D
解:A、两个图形不能完全重合,不是全等图形,不符合题意,
B.两个图形不能完全重合,不是全等图形,符合题意,
C.两个图形不能完全重合,不是全等图形,不符合题意,
D.两个图形能完全重合,是全等图形,不符合题意,
故选D.
2.C
解:①全等图形的形状和大小都相同,故此说法正确;
②全等三角形的对应角相等,故此说法正确;
③全等三角形的对应边的高相等,故此说法错误;
④全等三角形的对应边相等,故此说法正确.
故选C.
3.D
解:∵,∠DEB+∠DEC=180°,
∴,
又∵,
∴
∴,
即
故选:D.
4.D
解:设BE=t,则BF=2t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
情况一:当BE=AG,BF=AE时,
∵BF=AE,AB=6,
∴2t=6-t,
解得:t=2,
∴AG=BE=2;
情况二:当BE=AE,BF=AG时,
∵BE=AE,AB=6,
∴t=6-t,
解得:t=3,
∴AG=BF=2t=6,
综上所述,AG=2或AG=6.
故选D.
5.C
解:∵,
∴,
∴,∵,
在和中,
∴,故A正确;
∵,
在和中,
∴,故B正确;
∵,
在和中,
∴,故D正确;
C中条件不能证明.
6.C
解:,
同理可得:
全等三角形有△AEO≌△BFO,△CEO≌△DFO,△ACO≌△BDO,共3对,
故选:C.
7.A
解:在△ODA和△OCB中
∴△ODA≌△OCB(SAS),
∴∠D=∠C=25°,
∵∠O=60°,∠C=25°,
∴∠DBE=60°+25°=85°,
∴∠BED=180°?85°?25°=70°,
故选:A.
8.C
解:A、因为,所以,选项正确;
B、因为,所以正确;
C、由,可以得到,选项错误;
D、由,可得,选项正确.
故选:C
9.A
解:∵,
∴,
∵和为对顶角,
∴,
又∵,
∴.
故选:A.
10.C
解:∵BD⊥AE于D,CE⊥AE于E,
∴∠ADB=∠E=90,
在Rt△BAD和Rt△ACE中,
AB=AC、
AD=EC
∴△BAD≌△CAE(HL),
∴∠BAD=∠ACE,
∵∠ACE+∠CAE=90°,
∴∠BAC
=∠BAD+∠CAE=90°.
故选C.
11.C
解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故选:C.
12.B
解:延长BD交AC于点E,
∵平分,
∴,
∵,
∴,
∵AD=AD,
∴△ADB≌△ADE,
∴BD=ED,,
∴,
∴,
∴,
故选:B.
13.135
解:如图所示,
在△ACB和△DCE中,
,
∴,
∴,
∴;
故答案是:.
14.
解:∵△ABC≌△ADE,∠EAB=112°,
∴∠EAD=DAB=56°,∠D=∠B,
∴∠ACB+∠B=180°-56°=124°,
∵∠ACB=∠FCD,
∴∠FCD+∠D=124°,
∵∠EFC是△FCD的一个外角,
∴∠EFC=∠FCD+∠D=124°,
故答案为:124.
15.
解:∵AD=BC,BD=DB,
∴当添加AB=CD时,可根据“SSS”判断△ABD≌△CDB.
故答案为:AB=CD.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
16.
解:∵和是等腰直角三角形,
∴,
∴,
∴,
在和中,,
∴≌(SAS),
∴.
故答案为:BE.
17.HL
解:∵∠OMP=∠ONP=90°,且OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP是∠AOB的平分线.
故答案为:HL.
18.90
解:在△ABS与△CBD中,
∵,
∴△ABS≌△CBD(ASA),
∴AS=CD=90(米).
故答案是:90.
19.根据证明.
解:连接,,如图,
点分别是、的中点,
,,
在和中,
,
∴.
.
答:需要测量的长度,即为工件内槽宽.
其依据是根据证明;
故答案为:根据证明.
20.3
解:延长AP交BC于点E,如图所示.
∵AP垂直∠ABC的平分线BP于点P,
∴∠ABP=∠EBP.
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=EP.
∵△APC和△EPC等底同高,
∴S△APC=S△CPE,
∴S△PBC=S△BPE+S△CPE=S△ABC=×6=3(cm2),
故答案为:3.
21.20°
解:设,,
则,
,
∵,
∴,
∴,
∴,
∴,
∴,
解得,
∴.
22.与互相垂直且相等.证明见解析
解:与互相垂直且相等.
如图,延长交于点M.
∵,∠ACB=90°
,
∴,,
∵,
∴,
∴,
∴与互相垂直且相等.
23.见解析
解:证明:在△ABC和△ADC中,
∵,
∴△ABC≌△ADC(SSS),
∴∠BCF=∠DCF,
在△BCF和△DCF中,
∵,
∴△BCF≌△DCF(SAS),
∴BF=DF.
24.(1)见详解;(2)见详解
解:(1)证明:∵AB⊥AC,AD⊥AE,
∴∠BAC=∠DAE=90°,
∴∠BAC+∠BAE=∠DAE+∠BAE,
∴∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△ADB≌△AEC(SAS);
(2)由(1)知,△ADB≌△AEC,
∴∠ACE=∠ABD,
∵∠BAC=90°,
∴∠CBD+∠BCE=∠ABC+∠ACB=90°,
∴∠BFC=90°,
∴DB⊥EC.
25.(1)见详解;(2)
解:(1)证明:由题意得:,,
∴,
∴,
∴
在和中
,
∴;
(2)解:由题意得:,
∵,
∴,
∴,
答:两堵木墙之间的距离为.
26.(1)见解析;(2)
解:(1)证明:,
,
在和中,
,
;
(2),,
,
又∵,,
,
,
,
,
,
即.
27.猜想:DE=DF;探究:DE=DF,证明见解析;应用:S△DEF=8.
解:猜想:DE=DF.
如图1,连接CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为边AB的中点,
∴CD=AD,∠BCD=∠ACB=45°,
∴∠EAD=∠FCD,
在△AED和△CFD中,,
∴△ADE≌△CDF(SAS),
∴DE=DF,
故答案为:DE=DF;
探究:DE=DF,证明如下:
如图2,连接CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为AB中点,
∴AD=CD,∠BCD=∠ACB=45°,
∵∠CAD+∠EAD=∠BCD+∠FCD=180°,
∴∠EAD=∠FCD=135°,
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS),
∴DE=DF;
应用:
∵△ADE≌△CDF,
∴∠ADE=∠CDF,
∵∠ADC=90°,
∴∠EDF=90°,
∵DE=DF=4,
∴S△DEF=DE2=×42=8.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
