2021—2022学年人教版 九年级数学上册22.3 实际问题与二次函数 同步课时训练(word版、含答案)
文档属性
| 名称 | 2021—2022学年人教版 九年级数学上册22.3 实际问题与二次函数 同步课时训练(word版、含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 16:02:37 | ||
图片预览




文档简介
人教版
九年级数学上册
22.3
实际问题与二次函数
同步课时训练
一、选择题
1.
某种服装的销售利润y(万元)与销售数量x(万件)之间满足函数解析式y=-2x2+4x+5,则利润的( )
A.最大值为5万元
B.最大值为7万元
C.最小值为5万元
D.最小值为7万元
2.
某企业生产季节性产品,当产品无利润时,企业自动停产,经过调研,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=-n2+12n-11,则企业停产的月份为( )
A.1月和11月
B.1月、11月和12月
C.1月
D.1月至11月
3.
如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是y=-x2+x+,则该运动员此次掷铅球的成绩是( )
A.6
m
B.12
m
C.8
m
D.10
m
4.
中环桥是省城太原的一座跨汾河大桥(如图①),它由五个高度不同,跨径也不同的抛物线形钢拱通过吊杆,拉索与主梁相连.最高的钢拱如图②所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系.则此抛物线形钢拱的函数解析式为( )
A.y=x2
B.y=-x2
C.y=x2
D.y=-x2
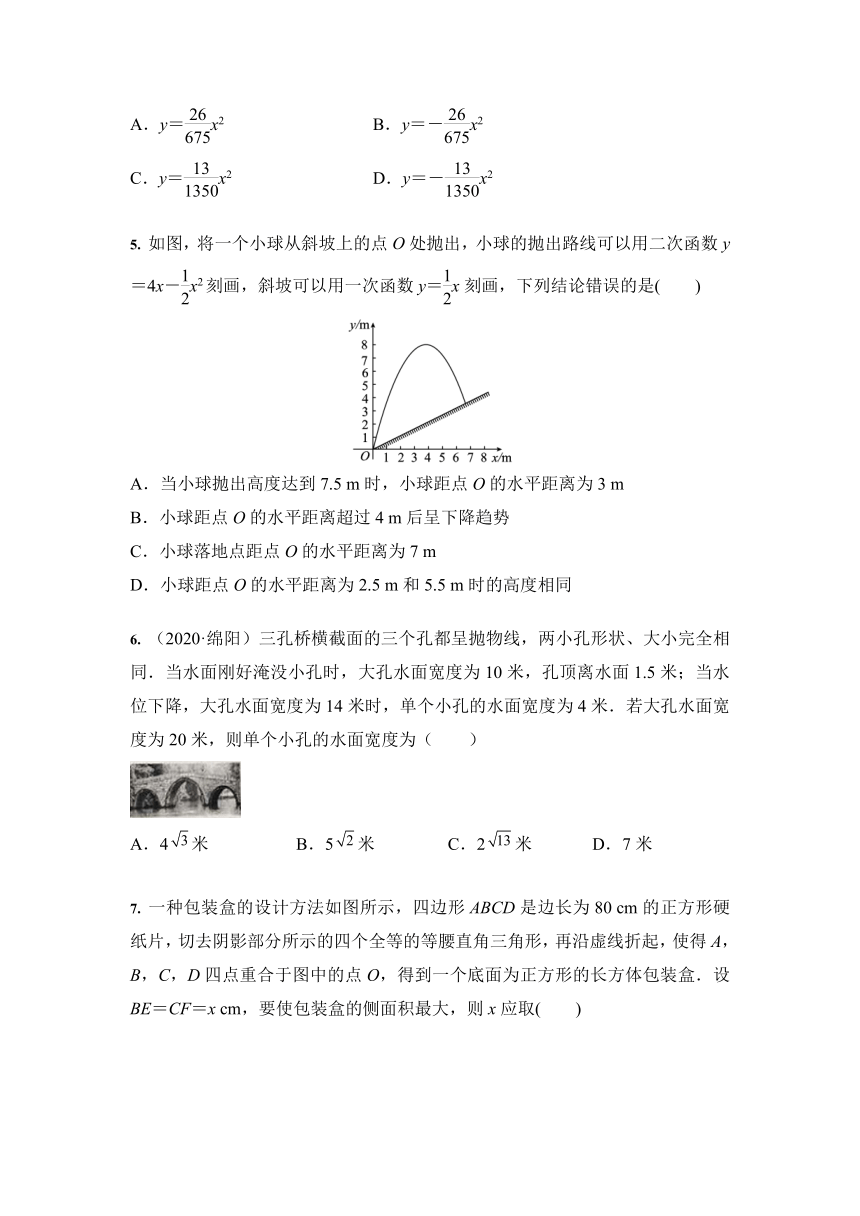
5.
如图,将一个小球从斜坡上的点O处抛出,小球的抛出路线可以用二次函数y=4x-x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5
m时,小球距点O的水平距离为3
m
B.小球距点O的水平距离超过4
m后呈下降趋势
C.小球落地点距点O的水平距离为7
m
D.小球距点O的水平距离为2.5
m和5.5
m时的高度相同
6.
(2020·绵阳)三孔桥横截面的三个孔都呈抛物线,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米.若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米
B.5米
C.2米
D.7米
7.
一种包装盒的设计方法如图所示,四边形ABCD是边长为80
cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,得到一个底面为正方形的长方体包装盒.设BE=CF=x
cm,要使包装盒的侧面积最大,则x应取( )
A.30
B.25
C.20
D.15
8.
一位篮球运动员在距离篮圈中心水平距离4
m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5
m时,达到最大高度3.5
m,然后准确落入篮筐内.已知篮圈中心距离地面高度为3.05
m,在如图
(示意图)所示的平面直角坐标系中,下列说法正确的是( )
A.此抛物线的解析式是y=-x2+3.5
B.篮圈中心的坐标是(4,3.05)
C.此抛物线的顶点坐标是(3.5,0)
D.篮球出手时离地面的高度是2
m
二、填空题
9.
某商店从厂家以每件21元的价格购进一批商品,该商品可以自行定价,若每件商品的售价为a元,则可卖出(350-10a)件.但物价部门限定每件商品加价不能超过进价的40%,若商店想获得最大利润,则每件商品的价格应定为________元.
10.
(2020·连云港)加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式y=-0.2x2+1.5x-2,则最佳加工时间为
▲
min.
11.
已知一个直角三角形两直角边长的和为30,则这个直角三角形的面积最大为________.
12.
(2020·天门仙桃潜江)某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为
元.
13.
飞机着落后滑行的距离s(单位:米)关于滑行时间t(单位:秒)的函数解析式是s=60t-t2,则飞机着落后滑行的最长时间为________秒.
14.
如图所示是一座抛物线形拱桥,当水面宽为12
m时,桥拱顶部离水面4
m,以水平方向为x轴,建立平面直角坐标系.若选取点A为坐标原点时的抛物线解析式为y=-(x-6)2+4,则选取点B为坐标原点时的抛物线解析式为________________.
15.
某大学生利用业余时间销售一种进价为60元/件的文化衫,前期了解并整理了销售这种文化衫的相关信息如下:
(1)月销量y(件)与售价x(元/件)的关系满足y=-2x+400;
(2)工商部门限制售价x满足70≤x≤150(计算月利润时不考虑其他成本).
给出下列结论:
①这种文化衫的月销量最小为100件;
②这种文化衫的月销量最大为260件;
③销售这种文化衫的月利润最小为2600元;
④销售这种文化衫的月利润最大为9000元.
其中正确的是________.(把所有正确结论的序号都填上)
16.
竖直上抛的小球离地高度是它运动时间的二次函数.小军相隔1秒依次竖直向上抛出两个小球.假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度.第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=________.
三、解答题
17.
养鸡专业户计划用116
m的篱笆围成如图所示的三间长方形鸡舍,门MN宽2
m,门PQ和RS的宽各为1
m,怎样设计才能使围成的鸡舍面积最大?
18.
如图,某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50
m.设饲养室的长为x(m),占地面积为y(m2).
(1)如图②,当饲养室的长x为多少时,占地面积y最大?
(2)如图③,现要求在图中所示位置留2
m宽的门,且仍使饲养室的占地面积最大.小敏说:“只要饲养室的长比(1)中的长多2
m就行了.”请你通过计算,判断小敏的说法是否正确.
19.
如图,工人师傅用一块长为10
dm,宽为6
dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形(厚度不计).
(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕,并求长方体底面面积为12
dm2时,裁掉的正方形的边长;
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长为多少时,总费用最低,最低为多少元?
20.
(2020·青岛)某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙,它由长形和抛物线构成,长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m.
(1)按如图①所示的直角坐标系,抛物线可以用(k≠0)表示.求该抛物线的函数表达式;
(2)现将A型活动板房改造为B型活动板房.如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/.已知GM=2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本)
(3)根据市场调查,以单价650元销售(2)中的B型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个.公司每月最多能生产160个B型活动板房.不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?
21.
(2020·成都)在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:件)与线下售价x(单位:元/件,12≤x<24)满足一次函数的关系,部分数据如下表:
(1)求y与x的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
人教版
九年级数学上册
22.3
实际问题与二次函数
同步课时训练-答案
一、选择题
1.
【答案】B
2.
【答案】B [解析]
由题意知,利润y和月份n之间的函数关系式为y=-n2+12n-11,
∴y=-(n-6)2+25,
当n=1时,y=0;
当n=11时,y=0;
当n=12时,y<0.
故停产的月份是1月、11月和12月.
故选B.
3.
【答案】D [解析]
把y=0代入y=-x2+x+,得-x2+x+=0,
解得x1=10,x2=-2.又∵x>0,∴x=10.
故选D.
4.
【答案】B [解析]
设二次函数的解析式为y=ax2.由题可知,点A的坐标为(-45,-78),代入解析式可得-78=a(-45)2,解得a=-,∴二次函数解析式为y=-x2.故选B.
5.
【答案】A [解析]
令y=7.5,得4x-x2=7.5.解得x1=3,x2=5.可见选项A错误.
由y=4x-x2得y=-(x-4)2+8,∴对称轴为直线x=4,当x>4时,y随x的增大而减小,选项B正确.
联立y=4x-x2与y=x,解得或∴抛物线与直线的交点坐标为(0,0),,可见选项C正确.
由对称性可知选项D正确.
综上所述,只有选项A中的结论是错误的,故选A.
6.
【答案】B
【解析】如图所示,建立平面直角坐标系.设大孔对应的函数关系式为y=ax2+c,过B
(5,c-1.5),F(7,0),则,解得,∴大孔对应的函数关系式为y=-0.06x2+2.94.当x=10时,y=-0.06×102+2.94=-3.06,∴H(0,-3.06).设右边小孔顶点坐标为D(10,1.44),则右边小孔对应的函数关系式为y=m(x-10)2+1.44,过点G(12,0),则0=
m(12-10)2+1.44,解得m=-0.36,∴右边小孔对应的函数关系式为y=-0.36(x-10)2+1.44,当y=-3.06时,-3.06=-0.36(x-10)2+1.44,解得x=10±,∴大孔水面宽度为20米,时单个小孔的水面宽度为5米.故选项B正确.
7.
【答案】C [解析]
如图,设BE=CF=x
cm,则EF=(80-2x)cm.∵△EFM和△CFN都是等腰直角三角形,
∴MF=EF=(40
-x)cm,FN=CF=x
cm,
∴包装盒的侧面积=4MF·FN=4·x(40
-x)=-8(x-20)2+3200,
故当x=20时,包装盒的侧面积最大.
8.
【答案】A [解析]
∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数解析式为y=ax2+3.5.
∵篮圈中心(1.5,3.05)在抛物线上,∴3.05=a×1.52+3.5.解得a=-.∴y=-x2+3.5.可见选项A正确.
由图示知,篮圈中心的坐标是(1.5,3.05),可见选项B错误.
由图示知,此抛物线的顶点坐标是(0,3.5),可见选项C错误.
将x=-2.5代入抛物线的解析式,得y=-×(-2.5)2+3.5=2.25,∴这次跳投时,球出手处离地面2.25
m可见选项D错误.
故选A.
二、填空题
9.
【答案】28 [解析]
设商店所获利润为y元.根据题意,得
y=(a-21)(350-10a)=-10a2+560a-7350=-10(a-28)2+490,
即当a=28时,可获得最大利润.
又21×(1+40%)=21×1.4=29.4,而28<29.4,所以a=28符合要求.
故商店应把每件商品的价格定为28元,此时可获得最大利润.
10.
【答案】3.75
【解析】本题考查了二次函数的性质,当加工时间x为何值时可食用率y最大,从而转化为二次函数的最值问题,由二次项系数为负,配方可知x=3.75时,y最在大,故答案为3.75.
11.
【答案】
12.
【答案】70
【解析】.设每顶头盔的售价为x元,
由题意,得:w=(x-50)×[(200+
(80-x)
×20],=(x-50)×(-20x+1800)
=-20x2+2800x-90000,
x=-,
∴当销售单价定为70元时,每月可获得最大利润.因此本题答案为70.
13.
【答案】20 [解析]
滑行的最长时间实际上是求顶点的横坐标.∵s=60t-t2=-(t-20)2+600,∴当t=20时,s的最大值为600.
14.
【答案】y=-(x+6)2+4
15.
【答案】①②③ [解析]
由题意知,当70≤x≤150时,y=-2x+400,
∵-2<0,∴y随x的增大而减小,
∴当x=150时,y取得最小值,最小值为100,故①正确;
当x=70时,y取得最大值,最大值为260,故②正确;
设销售这种文化衫的月利润为W元,
则W=(x-60)(-2x+400)=-2(x-130)2+9800,
∵70≤x≤150,
∴当x=70时,W取得最小值,最小值为-2(70-130)2+9800=2600,故③正确;
当x=130时,W取得最大值,最大值为9800,故④错误.
故答案为①②③.
16.
【答案】1.6
秒 【解析】本题主要考查了二次函数的对称性问题.由题意可知,各自抛出后1.1秒时到达相同最大离地高度,即到达二次函数图象的顶点处,故此二次函数图象的对称轴为t=1.1;由于两次抛小球的时间间隔为1秒,所以当第一个小球和第二个小球到达相同高度时,则这两个小球必分居对称轴左右两侧,由于高度相同,则在该时间节点上,两小球对应时间到对称轴距离相同.
故该距离为0.5秒,
所以此时第一个小球抛出后t=1.1+0.5=1.6秒时与第二个小球的离地高度相同.
三、解答题
17.
【答案】
解:设AB=x
m,则AD==(60-2x)m,鸡舍的面积为y
m2,根据题意,得
y=x(60-2x)=-2x2+60x=-2(x-15)2+450.
∵0∴当x=15时,y取得最大值,
即当AB=15
m时,鸡舍面积最大,此时AD=30
m.
答:当AD的长为30
m,AB的长为15
m时,围成的鸡舍面积最大.
18.
【答案】
解:(1)∵y=x·=-(x-25)2+,
∴当x=25时,占地面积y最大,
即当饲养室的长x为25
m时,占地面积y最大.
(2)∵y=x·=-(x-26)2+338,
∴当x=26时,占地面积y最大,
即当饲养室的长x为26
m时,占地面积y最大.
∵26-25=1≠2,∴小敏的说法不正确.
19.
【答案】
解:(1)如图所示:
设裁掉的正方形的边长为x
dm.
由题意可得(10-2x)(6-2x)=12,
即x2-8x+12=0,解得x1=2,x2=6(舍去).
答:当裁掉的正方形的边长为2
dm时,长方体底面面积为12
dm2.
(2)∵长方体的底面长不大于底面宽的五倍,
∴10-2x≤5(6-2x),解得x≤2.5,
∴0设总费用为w元,由题意可知
w=0.5×2x(16-4x)+2(10-2x)(6-2x)=4x2-48x+120=4(x-6)2-24.
∵此函数图象的对称轴为直线x=6,图象开口向上,
∴当0<x≤2.5时,w随x的增大而减小,
∴当x=2.5时,w有最小值,最小值为25.
答:当裁掉的正方形边长为2.5
dm时,总费用最低,最低为25元.
20.
【答案】
解:(1)由题意得AD=4,AB=3,EH=4,
∴OA=OD=AD=×4=2,OE=EH-OH=EH-AB=4-3=1,
∴A(-2,0),E(0,1),
∴,解得,
∴该抛物线的函数表达式为:.
(2)由题意得OM=GM=×2=1,∴当x=1时,,∴MN=.
∴每个B型活动板房的成本是:425+50×4×=575(元).
(3)由题意得=
===
由得620≤n≤650.
∵的对称轴在620≤n≤650之内,
∴当公司将销售单价n(元)定为637.5时,每月销售B型活动板房所获利润w(元)最大,最大利润是:
=62.5×125=7812.5(元).
21.
【答案】
解:(1)∵y与x满足一次函数的关系,∴设y=kx+b,
将x=12,y=1200;x=13,y=1100代入得:,解得:,
∴y与x的函数关系式为:y=﹣100x+2400;
(2)设线上和线下月利润总和为m元,
则m=400(x﹣2﹣10)+y(x﹣10)=400x﹣4800+(﹣100x+2400)(x﹣10)=﹣100(x﹣19)2+7300,
∴当x为19元/件时,线上和线下月利润总和达到最大,此时的最大利润为7300元.
【解析】(1)由待定系数法求出y与x的函数关系式即可;
(2)设线上和线下月利润总和为m元,则m=400(x﹣2﹣10)+y(x﹣10)=400x﹣4800+(﹣100x+2400)(x﹣10)=﹣100(x﹣19)2+7300,由二次函数的性质即可得出答案.
九年级数学上册
22.3
实际问题与二次函数
同步课时训练
一、选择题
1.
某种服装的销售利润y(万元)与销售数量x(万件)之间满足函数解析式y=-2x2+4x+5,则利润的( )
A.最大值为5万元
B.最大值为7万元
C.最小值为5万元
D.最小值为7万元
2.
某企业生产季节性产品,当产品无利润时,企业自动停产,经过调研,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=-n2+12n-11,则企业停产的月份为( )
A.1月和11月
B.1月、11月和12月
C.1月
D.1月至11月
3.
如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是y=-x2+x+,则该运动员此次掷铅球的成绩是( )
A.6
m
B.12
m
C.8
m
D.10
m
4.
中环桥是省城太原的一座跨汾河大桥(如图①),它由五个高度不同,跨径也不同的抛物线形钢拱通过吊杆,拉索与主梁相连.最高的钢拱如图②所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系.则此抛物线形钢拱的函数解析式为( )
A.y=x2
B.y=-x2
C.y=x2
D.y=-x2
5.
如图,将一个小球从斜坡上的点O处抛出,小球的抛出路线可以用二次函数y=4x-x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5
m时,小球距点O的水平距离为3
m
B.小球距点O的水平距离超过4
m后呈下降趋势
C.小球落地点距点O的水平距离为7
m
D.小球距点O的水平距离为2.5
m和5.5
m时的高度相同
6.
(2020·绵阳)三孔桥横截面的三个孔都呈抛物线,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米.若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米
B.5米
C.2米
D.7米
7.
一种包装盒的设计方法如图所示,四边形ABCD是边长为80
cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,得到一个底面为正方形的长方体包装盒.设BE=CF=x
cm,要使包装盒的侧面积最大,则x应取( )
A.30
B.25
C.20
D.15
8.
一位篮球运动员在距离篮圈中心水平距离4
m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5
m时,达到最大高度3.5
m,然后准确落入篮筐内.已知篮圈中心距离地面高度为3.05
m,在如图
(示意图)所示的平面直角坐标系中,下列说法正确的是( )
A.此抛物线的解析式是y=-x2+3.5
B.篮圈中心的坐标是(4,3.05)
C.此抛物线的顶点坐标是(3.5,0)
D.篮球出手时离地面的高度是2
m
二、填空题
9.
某商店从厂家以每件21元的价格购进一批商品,该商品可以自行定价,若每件商品的售价为a元,则可卖出(350-10a)件.但物价部门限定每件商品加价不能超过进价的40%,若商店想获得最大利润,则每件商品的价格应定为________元.
10.
(2020·连云港)加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式y=-0.2x2+1.5x-2,则最佳加工时间为
▲
min.
11.
已知一个直角三角形两直角边长的和为30,则这个直角三角形的面积最大为________.
12.
(2020·天门仙桃潜江)某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为
元.
13.
飞机着落后滑行的距离s(单位:米)关于滑行时间t(单位:秒)的函数解析式是s=60t-t2,则飞机着落后滑行的最长时间为________秒.
14.
如图所示是一座抛物线形拱桥,当水面宽为12
m时,桥拱顶部离水面4
m,以水平方向为x轴,建立平面直角坐标系.若选取点A为坐标原点时的抛物线解析式为y=-(x-6)2+4,则选取点B为坐标原点时的抛物线解析式为________________.
15.
某大学生利用业余时间销售一种进价为60元/件的文化衫,前期了解并整理了销售这种文化衫的相关信息如下:
(1)月销量y(件)与售价x(元/件)的关系满足y=-2x+400;
(2)工商部门限制售价x满足70≤x≤150(计算月利润时不考虑其他成本).
给出下列结论:
①这种文化衫的月销量最小为100件;
②这种文化衫的月销量最大为260件;
③销售这种文化衫的月利润最小为2600元;
④销售这种文化衫的月利润最大为9000元.
其中正确的是________.(把所有正确结论的序号都填上)
16.
竖直上抛的小球离地高度是它运动时间的二次函数.小军相隔1秒依次竖直向上抛出两个小球.假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度.第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=________.
三、解答题
17.
养鸡专业户计划用116
m的篱笆围成如图所示的三间长方形鸡舍,门MN宽2
m,门PQ和RS的宽各为1
m,怎样设计才能使围成的鸡舍面积最大?
18.
如图,某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50
m.设饲养室的长为x(m),占地面积为y(m2).
(1)如图②,当饲养室的长x为多少时,占地面积y最大?
(2)如图③,现要求在图中所示位置留2
m宽的门,且仍使饲养室的占地面积最大.小敏说:“只要饲养室的长比(1)中的长多2
m就行了.”请你通过计算,判断小敏的说法是否正确.
19.
如图,工人师傅用一块长为10
dm,宽为6
dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形(厚度不计).
(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕,并求长方体底面面积为12
dm2时,裁掉的正方形的边长;
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长为多少时,总费用最低,最低为多少元?
20.
(2020·青岛)某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙,它由长形和抛物线构成,长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m.
(1)按如图①所示的直角坐标系,抛物线可以用(k≠0)表示.求该抛物线的函数表达式;
(2)现将A型活动板房改造为B型活动板房.如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/.已知GM=2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本)
(3)根据市场调查,以单价650元销售(2)中的B型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个.公司每月最多能生产160个B型活动板房.不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?
21.
(2020·成都)在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:件)与线下售价x(单位:元/件,12≤x<24)满足一次函数的关系,部分数据如下表:
(1)求y与x的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
人教版
九年级数学上册
22.3
实际问题与二次函数
同步课时训练-答案
一、选择题
1.
【答案】B
2.
【答案】B [解析]
由题意知,利润y和月份n之间的函数关系式为y=-n2+12n-11,
∴y=-(n-6)2+25,
当n=1时,y=0;
当n=11时,y=0;
当n=12时,y<0.
故停产的月份是1月、11月和12月.
故选B.
3.
【答案】D [解析]
把y=0代入y=-x2+x+,得-x2+x+=0,
解得x1=10,x2=-2.又∵x>0,∴x=10.
故选D.
4.
【答案】B [解析]
设二次函数的解析式为y=ax2.由题可知,点A的坐标为(-45,-78),代入解析式可得-78=a(-45)2,解得a=-,∴二次函数解析式为y=-x2.故选B.
5.
【答案】A [解析]
令y=7.5,得4x-x2=7.5.解得x1=3,x2=5.可见选项A错误.
由y=4x-x2得y=-(x-4)2+8,∴对称轴为直线x=4,当x>4时,y随x的增大而减小,选项B正确.
联立y=4x-x2与y=x,解得或∴抛物线与直线的交点坐标为(0,0),,可见选项C正确.
由对称性可知选项D正确.
综上所述,只有选项A中的结论是错误的,故选A.
6.
【答案】B
【解析】如图所示,建立平面直角坐标系.设大孔对应的函数关系式为y=ax2+c,过B
(5,c-1.5),F(7,0),则,解得,∴大孔对应的函数关系式为y=-0.06x2+2.94.当x=10时,y=-0.06×102+2.94=-3.06,∴H(0,-3.06).设右边小孔顶点坐标为D(10,1.44),则右边小孔对应的函数关系式为y=m(x-10)2+1.44,过点G(12,0),则0=
m(12-10)2+1.44,解得m=-0.36,∴右边小孔对应的函数关系式为y=-0.36(x-10)2+1.44,当y=-3.06时,-3.06=-0.36(x-10)2+1.44,解得x=10±,∴大孔水面宽度为20米,时单个小孔的水面宽度为5米.故选项B正确.
7.
【答案】C [解析]
如图,设BE=CF=x
cm,则EF=(80-2x)cm.∵△EFM和△CFN都是等腰直角三角形,
∴MF=EF=(40
-x)cm,FN=CF=x
cm,
∴包装盒的侧面积=4MF·FN=4·x(40
-x)=-8(x-20)2+3200,
故当x=20时,包装盒的侧面积最大.
8.
【答案】A [解析]
∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数解析式为y=ax2+3.5.
∵篮圈中心(1.5,3.05)在抛物线上,∴3.05=a×1.52+3.5.解得a=-.∴y=-x2+3.5.可见选项A正确.
由图示知,篮圈中心的坐标是(1.5,3.05),可见选项B错误.
由图示知,此抛物线的顶点坐标是(0,3.5),可见选项C错误.
将x=-2.5代入抛物线的解析式,得y=-×(-2.5)2+3.5=2.25,∴这次跳投时,球出手处离地面2.25
m可见选项D错误.
故选A.
二、填空题
9.
【答案】28 [解析]
设商店所获利润为y元.根据题意,得
y=(a-21)(350-10a)=-10a2+560a-7350=-10(a-28)2+490,
即当a=28时,可获得最大利润.
又21×(1+40%)=21×1.4=29.4,而28<29.4,所以a=28符合要求.
故商店应把每件商品的价格定为28元,此时可获得最大利润.
10.
【答案】3.75
【解析】本题考查了二次函数的性质,当加工时间x为何值时可食用率y最大,从而转化为二次函数的最值问题,由二次项系数为负,配方可知x=3.75时,y最在大,故答案为3.75.
11.
【答案】
12.
【答案】70
【解析】.设每顶头盔的售价为x元,
由题意,得:w=(x-50)×[(200+
(80-x)
×20],=(x-50)×(-20x+1800)
=-20x2+2800x-90000,
x=-,
∴当销售单价定为70元时,每月可获得最大利润.因此本题答案为70.
13.
【答案】20 [解析]
滑行的最长时间实际上是求顶点的横坐标.∵s=60t-t2=-(t-20)2+600,∴当t=20时,s的最大值为600.
14.
【答案】y=-(x+6)2+4
15.
【答案】①②③ [解析]
由题意知,当70≤x≤150时,y=-2x+400,
∵-2<0,∴y随x的增大而减小,
∴当x=150时,y取得最小值,最小值为100,故①正确;
当x=70时,y取得最大值,最大值为260,故②正确;
设销售这种文化衫的月利润为W元,
则W=(x-60)(-2x+400)=-2(x-130)2+9800,
∵70≤x≤150,
∴当x=70时,W取得最小值,最小值为-2(70-130)2+9800=2600,故③正确;
当x=130时,W取得最大值,最大值为9800,故④错误.
故答案为①②③.
16.
【答案】1.6
秒 【解析】本题主要考查了二次函数的对称性问题.由题意可知,各自抛出后1.1秒时到达相同最大离地高度,即到达二次函数图象的顶点处,故此二次函数图象的对称轴为t=1.1;由于两次抛小球的时间间隔为1秒,所以当第一个小球和第二个小球到达相同高度时,则这两个小球必分居对称轴左右两侧,由于高度相同,则在该时间节点上,两小球对应时间到对称轴距离相同.
故该距离为0.5秒,
所以此时第一个小球抛出后t=1.1+0.5=1.6秒时与第二个小球的离地高度相同.
三、解答题
17.
【答案】
解:设AB=x
m,则AD==(60-2x)m,鸡舍的面积为y
m2,根据题意,得
y=x(60-2x)=-2x2+60x=-2(x-15)2+450.
∵0
即当AB=15
m时,鸡舍面积最大,此时AD=30
m.
答:当AD的长为30
m,AB的长为15
m时,围成的鸡舍面积最大.
18.
【答案】
解:(1)∵y=x·=-(x-25)2+,
∴当x=25时,占地面积y最大,
即当饲养室的长x为25
m时,占地面积y最大.
(2)∵y=x·=-(x-26)2+338,
∴当x=26时,占地面积y最大,
即当饲养室的长x为26
m时,占地面积y最大.
∵26-25=1≠2,∴小敏的说法不正确.
19.
【答案】
解:(1)如图所示:
设裁掉的正方形的边长为x
dm.
由题意可得(10-2x)(6-2x)=12,
即x2-8x+12=0,解得x1=2,x2=6(舍去).
答:当裁掉的正方形的边长为2
dm时,长方体底面面积为12
dm2.
(2)∵长方体的底面长不大于底面宽的五倍,
∴10-2x≤5(6-2x),解得x≤2.5,
∴0
w=0.5×2x(16-4x)+2(10-2x)(6-2x)=4x2-48x+120=4(x-6)2-24.
∵此函数图象的对称轴为直线x=6,图象开口向上,
∴当0<x≤2.5时,w随x的增大而减小,
∴当x=2.5时,w有最小值,最小值为25.
答:当裁掉的正方形边长为2.5
dm时,总费用最低,最低为25元.
20.
【答案】
解:(1)由题意得AD=4,AB=3,EH=4,
∴OA=OD=AD=×4=2,OE=EH-OH=EH-AB=4-3=1,
∴A(-2,0),E(0,1),
∴,解得,
∴该抛物线的函数表达式为:.
(2)由题意得OM=GM=×2=1,∴当x=1时,,∴MN=.
∴每个B型活动板房的成本是:425+50×4×=575(元).
(3)由题意得=
===
由得620≤n≤650.
∵的对称轴在620≤n≤650之内,
∴当公司将销售单价n(元)定为637.5时,每月销售B型活动板房所获利润w(元)最大,最大利润是:
=62.5×125=7812.5(元).
21.
【答案】
解:(1)∵y与x满足一次函数的关系,∴设y=kx+b,
将x=12,y=1200;x=13,y=1100代入得:,解得:,
∴y与x的函数关系式为:y=﹣100x+2400;
(2)设线上和线下月利润总和为m元,
则m=400(x﹣2﹣10)+y(x﹣10)=400x﹣4800+(﹣100x+2400)(x﹣10)=﹣100(x﹣19)2+7300,
∴当x为19元/件时,线上和线下月利润总和达到最大,此时的最大利润为7300元.
【解析】(1)由待定系数法求出y与x的函数关系式即可;
(2)设线上和线下月利润总和为m元,则m=400(x﹣2﹣10)+y(x﹣10)=400x﹣4800+(﹣100x+2400)(x﹣10)=﹣100(x﹣19)2+7300,由二次函数的性质即可得出答案.
同课章节目录
