2021-2022学年人教版 九年级数学上册25.2 用列举法求概率 同步课时训练(word含答案)
文档属性
| 名称 | 2021-2022学年人教版 九年级数学上册25.2 用列举法求概率 同步课时训练(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 15:49:36 | ||
图片预览



文档简介
人教版
九年级数学上册
25.2
用列举法求概率
同步课时训练
一、选择题
1.
有A,B两个不透明的口袋,每个口袋里装有两个相同的球,A袋中的两个球上分别写有“细”“致”的字样,B袋中的两个球上分别写有“信”“心”的字样,从每个口袋里各摸出一个球,刚好能组成“细心”字样的概率是( )
A.
B.
C.
D.
2.
从同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为( )
A.
B.
C.
D.
3.
三名九年级同学坐在仅有的三个座位上,起身后重新就座,恰好有两名同学没有坐回原位的概率是
( )
A.
B.
C.
D.
4.
甲、乙两人用如图所示的两个转盘(每个转盘被分成面积相等的3个扇形)做游戏,游戏规则:转动两个转盘各一次,转盘停止后,若指针所在区域的数字之和为偶数,则甲获胜;若数字之和为奇数,则乙获胜;若指针落在分界线上,则重新转动转盘.甲获胜的概率是( )
A.
B.
C.
D.
5.
如图,有一块质地均匀的圆铁片,两面上分别写有数字1,2,有一个均匀的三棱锥旋转器和一个均匀的四棱锥旋转器,它们的侧面上分别写有数字1,2,3和数字1,2,3,4.在桌面上同时旋转这三件器物,停下来后,面向桌面的三个数字的积为奇数的概率是( )
A.
B.
C.
D.
6.
在-2,-1,0,1,2这五个数中任取两数m,n,则二次函数y=(x-m)2+n的图象的顶点在坐标轴上的概率为( )
A.
B.
C.
D.
7.
从长度分别为2,3,4,5的4条线段中任取三条,能构成直角三角形的概率为( )
A.
B.
C.
D.
8.
如图,在4×4的正方形网格中,阴影部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂上阴影,使阴影部分的图形仍然构成一个轴对称图形的概率是( )
A.
B.
C.
D.
二、填空题
9.
2018·滨州若从-1,1,2这三个数中任取两个分别作为点M的横、纵坐标,则点M在第二象限的概率是________.
10.
学校组织团员参加实践活动,共安排2辆车,小王和小李随机上了1辆车,结果他们同车的概率是________.
11.
三名运动员参加定点投篮比赛,原定出场顺序是:甲第一个出场,乙第二个出场,丙第三个出场.由于某种原因,要求这三名运动员用抽签方式重新确定出场顺序,则抽签后每个运动员的出场顺序都发生变化的概率为________.
12.
掷一枚硬币三次,其中有两次正面朝上、一次反面朝上的概率为________.
13.
分别写有数字,,-1,0,π的五张大小和质地均相同的卡片,从中任意抽取一张,抽到无理数的概率是________.
14.
从2019年高中一年级学生开始,湖南省全面启动高考综合改革,学生学习完必修课程后,可以根据高校相关专业的选课要求和自身兴趣、志向、优势,从思想政治、历史、地理、物理、化学、生物6个科目中,自主选择3个科目参加等级考试.学生A已选物理,还要从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科,则选修地理和生物的概率为________.
15.
如图,A是正方体小木块(质地均匀)的一个顶点,将小木块随机投掷在水平桌面上,则点A与桌面接触的概率是________.
16.
任取不等式组的一个整数解,则能使关于x的方程2x+k=-1的解为非负数的概率为________.
三、解答题
17.
甲同学口袋中有三张卡片,分别写着数字1、1、2,乙同学口袋中也有三张卡片,分别写着数字1、2、2.两人各自从自己的口袋中随机摸出一张卡片,若两人摸出的卡片上的数字之和为偶数,则甲胜;否则乙胜.求甲胜的概率.
18.
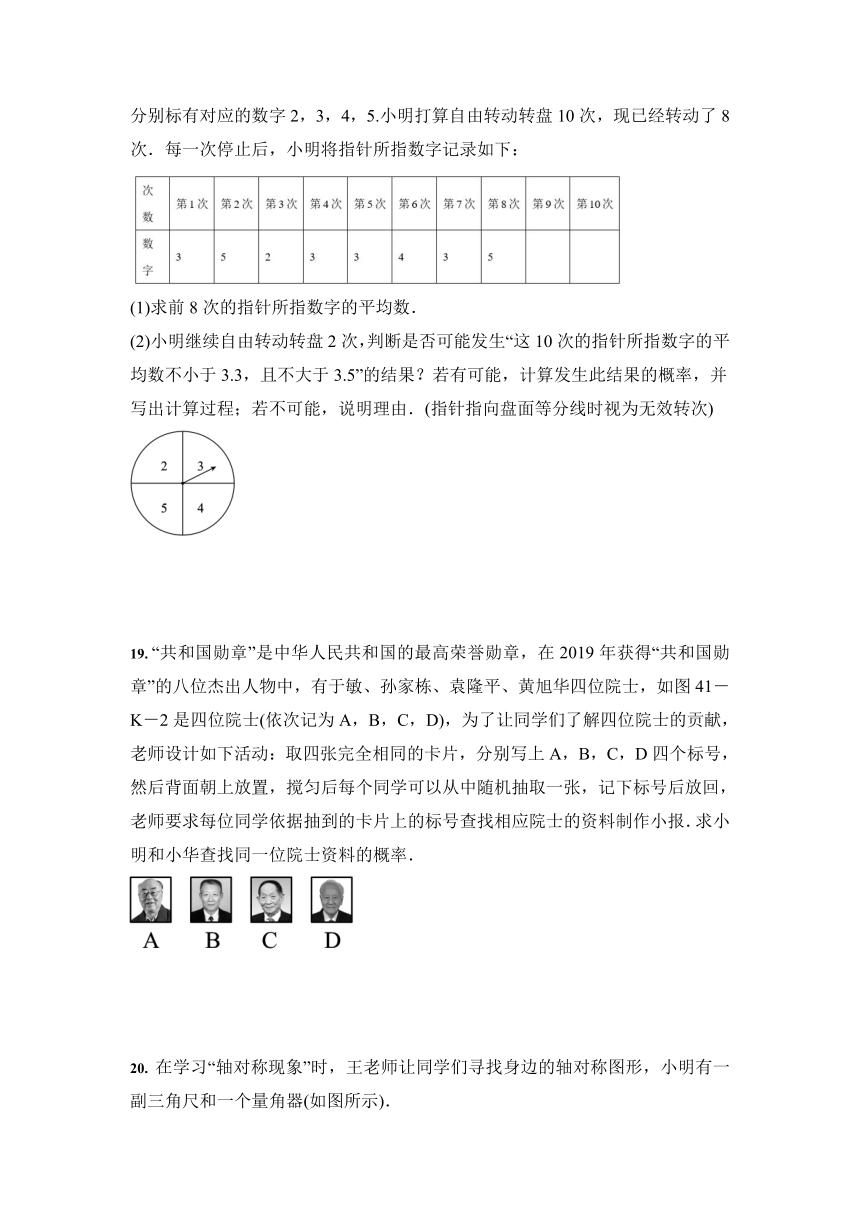
如图所示,有一个可以自由转动的转盘,其盘面被分为4等份,在每一等份分别标有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次.每一次停止后,小明将指针所指数字记录如下:
(1)求前8次的指针所指数字的平均数.
(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大于3.5”的结果?若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面等分线时视为无效转次)
19.
“共和国勋章”是中华人民共和国的最高荣誉勋章,在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士,如图41-K-2是四位院士(依次记为A,B,C,D),为了让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上A,B,C,D四个标号,然后背面朝上放置,搅匀后每个同学可以从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料制作小报.求小明和小华查找同一位院士资料的概率.
20.
在学习“轴对称现象”时,王老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).
(1)小明在这三件文具中任取一件,结果是轴对称图形的概率是________;
(2)小明把A,B两把三角尺的各任意一个角拼在一起(无重叠、无缝隙),得到一个更大的角,请画树状图或列表求这个角是钝角的概率.
人教版
九年级数学上册
25.2
用列举法求概率
同步课时训练-答案
一、选择题
1.
【答案】B [解析]
从每个口袋里各摸出一个球,有“细信”“细心”“致信”“致心”4种等可能的结果,其中组成“细心”字样的有1种结果,故概率是.
2.
【答案】A
3.
【答案】D [解析]
利用列举法可知,三人全部的坐法有6种,其中恰好有两名同学没有坐回原位的情况有3种,因此恰好有两名同学没有坐回原位的概率是=.
故选D.
4.
【答案】C [解析]
列表得:
所以甲获胜的概率是.
5.
【答案】C [解析]
画树状图如下:
因为共有24种等可能结果,面向桌面的三个数字的积为奇数的结果有4种,所以所求概率为.
6.
【答案】A [解析]
画树状图如下:
由树状图可知,共有20种等可能的结果,其中取到0的结果有8种,
所以函数图象的顶点在坐标轴上的概率为=.
7.
【答案】D [解析]
一共有四种可能,分别是2,3,4;2,3,5;2,4,5;3,4,5.其中只有长度分别是3,4,5的三条线段能构成直角三角形,所以能构成直角三角形的概率为.
8.
【答案】B [解析]
因为根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,白色的小正方形有13个,共13种情况,而能构成一个轴对称图形的有下列5种情况:
所以使图中阴影部分的图形仍然构成一个轴对称图形的概率是.故选B.
二、填空题
9.
【答案】 [解析]
若从-1,1,2这三个数中任取两个分别作为点M的横、纵坐标,一共有(-1,1),(-1,2),(1,-1),(1,2),(2,-1),(2,1)6种等可能结果,其中在第二象限的结果一共有2种,所以点M在第二象限的概率是.
10.
【答案】
11.
【答案】 【解析】根据题意画树状图如解图,每个运动员抽签的可能性相等,∵每个运动员的出场顺序都发生变化的有下列两种情况:乙、丙、甲;丙、甲、乙,∴每个运动员的出场顺序都发生变化的概率==.
12.
【答案】 [解析]
画树状图如下:
∵共有8种等可能的结果,其中有两次正面朝上、一次反面朝上的结果有3种,
∴掷一枚硬币三次,其中有两次正面朝上、一次反面朝上的概率为.
13.
【答案】 [解析]
五个数中和π是无理数,故从中任意抽取一张,抽到无理数的概率是.
14.
【答案】 [解析]
画树状图如下:
由图可知,选修结果共有6种,每种结果出现的可能性相等,其中选修地理和生物的结果只有1种,因此所求概率为.
15.
【答案】 [解析]
正方体小木块共有6个面,其中包含点A的面有3个,所以P(点A与桌面接触)==.
16.
【答案】 [解析]
因为不等式组的解集为-<k≤3,
所以不等式组的整数解为-2,-1,0,1,2,3.
关于x的方程2x+k=-1的解为x=-.
因为关于x的方程2x+k=-1的解为非负数,
所以k+1≤0,解得k≤-1,
所以能使关于x的方程2x+k=-1的解为非负数的k的值为-1,-2,
所以能使关于x的方程2x+k=-1的解为非负数的概率为=.
三、解答题
17.
【答案】
解:所有可能的结果列表如下:
甲乙
1
1
2
1
偶数
偶数
奇数
2
奇数
奇数
偶数
2
奇数
奇数
偶数
由表可知,和为偶数的结果有4种,∴P(甲胜)=.
答:甲胜的概率是.
18.
【答案】
解:(1)=3.5.
答:前8次的指针所指数字的平均数为3.5.
(2)可能.
若这10次的指针所指数字的平均数不小于3.3,且不大于3.5,则所指数字之和应不小于33,且不大于35.而前8次所指数字之和为28,所以最后2次所指数字之和应不小于5,且不大于7.
第9次和第10次指针可能所指的数字如下表所示:
一共有16种等可能的结果,其中指针所指数字之和不小于5,且不大于7的结果有9种,其概率为.
19.
【答案】
解:根据题意画树状图如下:
共有16种等可能的结果,其中小明和小华查找同一位院士资料的结果有4种,所以小明和小华查找同一位院士资料的概率为=.
20.
【答案】
解:(1)
(2)画树状图如图所示.
一共有9种等可能的结果,其中能得到钝角的结果有6种,所以这个角是钝角的概率是=.
九年级数学上册
25.2
用列举法求概率
同步课时训练
一、选择题
1.
有A,B两个不透明的口袋,每个口袋里装有两个相同的球,A袋中的两个球上分别写有“细”“致”的字样,B袋中的两个球上分别写有“信”“心”的字样,从每个口袋里各摸出一个球,刚好能组成“细心”字样的概率是( )
A.
B.
C.
D.
2.
从同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为( )
A.
B.
C.
D.
3.
三名九年级同学坐在仅有的三个座位上,起身后重新就座,恰好有两名同学没有坐回原位的概率是
( )
A.
B.
C.
D.
4.
甲、乙两人用如图所示的两个转盘(每个转盘被分成面积相等的3个扇形)做游戏,游戏规则:转动两个转盘各一次,转盘停止后,若指针所在区域的数字之和为偶数,则甲获胜;若数字之和为奇数,则乙获胜;若指针落在分界线上,则重新转动转盘.甲获胜的概率是( )
A.
B.
C.
D.
5.
如图,有一块质地均匀的圆铁片,两面上分别写有数字1,2,有一个均匀的三棱锥旋转器和一个均匀的四棱锥旋转器,它们的侧面上分别写有数字1,2,3和数字1,2,3,4.在桌面上同时旋转这三件器物,停下来后,面向桌面的三个数字的积为奇数的概率是( )
A.
B.
C.
D.
6.
在-2,-1,0,1,2这五个数中任取两数m,n,则二次函数y=(x-m)2+n的图象的顶点在坐标轴上的概率为( )
A.
B.
C.
D.
7.
从长度分别为2,3,4,5的4条线段中任取三条,能构成直角三角形的概率为( )
A.
B.
C.
D.
8.
如图,在4×4的正方形网格中,阴影部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂上阴影,使阴影部分的图形仍然构成一个轴对称图形的概率是( )
A.
B.
C.
D.
二、填空题
9.
2018·滨州若从-1,1,2这三个数中任取两个分别作为点M的横、纵坐标,则点M在第二象限的概率是________.
10.
学校组织团员参加实践活动,共安排2辆车,小王和小李随机上了1辆车,结果他们同车的概率是________.
11.
三名运动员参加定点投篮比赛,原定出场顺序是:甲第一个出场,乙第二个出场,丙第三个出场.由于某种原因,要求这三名运动员用抽签方式重新确定出场顺序,则抽签后每个运动员的出场顺序都发生变化的概率为________.
12.
掷一枚硬币三次,其中有两次正面朝上、一次反面朝上的概率为________.
13.
分别写有数字,,-1,0,π的五张大小和质地均相同的卡片,从中任意抽取一张,抽到无理数的概率是________.
14.
从2019年高中一年级学生开始,湖南省全面启动高考综合改革,学生学习完必修课程后,可以根据高校相关专业的选课要求和自身兴趣、志向、优势,从思想政治、历史、地理、物理、化学、生物6个科目中,自主选择3个科目参加等级考试.学生A已选物理,还要从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科,则选修地理和生物的概率为________.
15.
如图,A是正方体小木块(质地均匀)的一个顶点,将小木块随机投掷在水平桌面上,则点A与桌面接触的概率是________.
16.
任取不等式组的一个整数解,则能使关于x的方程2x+k=-1的解为非负数的概率为________.
三、解答题
17.
甲同学口袋中有三张卡片,分别写着数字1、1、2,乙同学口袋中也有三张卡片,分别写着数字1、2、2.两人各自从自己的口袋中随机摸出一张卡片,若两人摸出的卡片上的数字之和为偶数,则甲胜;否则乙胜.求甲胜的概率.
18.
如图所示,有一个可以自由转动的转盘,其盘面被分为4等份,在每一等份分别标有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次.每一次停止后,小明将指针所指数字记录如下:
(1)求前8次的指针所指数字的平均数.
(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大于3.5”的结果?若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面等分线时视为无效转次)
19.
“共和国勋章”是中华人民共和国的最高荣誉勋章,在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士,如图41-K-2是四位院士(依次记为A,B,C,D),为了让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上A,B,C,D四个标号,然后背面朝上放置,搅匀后每个同学可以从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料制作小报.求小明和小华查找同一位院士资料的概率.
20.
在学习“轴对称现象”时,王老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).
(1)小明在这三件文具中任取一件,结果是轴对称图形的概率是________;
(2)小明把A,B两把三角尺的各任意一个角拼在一起(无重叠、无缝隙),得到一个更大的角,请画树状图或列表求这个角是钝角的概率.
人教版
九年级数学上册
25.2
用列举法求概率
同步课时训练-答案
一、选择题
1.
【答案】B [解析]
从每个口袋里各摸出一个球,有“细信”“细心”“致信”“致心”4种等可能的结果,其中组成“细心”字样的有1种结果,故概率是.
2.
【答案】A
3.
【答案】D [解析]
利用列举法可知,三人全部的坐法有6种,其中恰好有两名同学没有坐回原位的情况有3种,因此恰好有两名同学没有坐回原位的概率是=.
故选D.
4.
【答案】C [解析]
列表得:
所以甲获胜的概率是.
5.
【答案】C [解析]
画树状图如下:
因为共有24种等可能结果,面向桌面的三个数字的积为奇数的结果有4种,所以所求概率为.
6.
【答案】A [解析]
画树状图如下:
由树状图可知,共有20种等可能的结果,其中取到0的结果有8种,
所以函数图象的顶点在坐标轴上的概率为=.
7.
【答案】D [解析]
一共有四种可能,分别是2,3,4;2,3,5;2,4,5;3,4,5.其中只有长度分别是3,4,5的三条线段能构成直角三角形,所以能构成直角三角形的概率为.
8.
【答案】B [解析]
因为根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,白色的小正方形有13个,共13种情况,而能构成一个轴对称图形的有下列5种情况:
所以使图中阴影部分的图形仍然构成一个轴对称图形的概率是.故选B.
二、填空题
9.
【答案】 [解析]
若从-1,1,2这三个数中任取两个分别作为点M的横、纵坐标,一共有(-1,1),(-1,2),(1,-1),(1,2),(2,-1),(2,1)6种等可能结果,其中在第二象限的结果一共有2种,所以点M在第二象限的概率是.
10.
【答案】
11.
【答案】 【解析】根据题意画树状图如解图,每个运动员抽签的可能性相等,∵每个运动员的出场顺序都发生变化的有下列两种情况:乙、丙、甲;丙、甲、乙,∴每个运动员的出场顺序都发生变化的概率==.
12.
【答案】 [解析]
画树状图如下:
∵共有8种等可能的结果,其中有两次正面朝上、一次反面朝上的结果有3种,
∴掷一枚硬币三次,其中有两次正面朝上、一次反面朝上的概率为.
13.
【答案】 [解析]
五个数中和π是无理数,故从中任意抽取一张,抽到无理数的概率是.
14.
【答案】 [解析]
画树状图如下:
由图可知,选修结果共有6种,每种结果出现的可能性相等,其中选修地理和生物的结果只有1种,因此所求概率为.
15.
【答案】 [解析]
正方体小木块共有6个面,其中包含点A的面有3个,所以P(点A与桌面接触)==.
16.
【答案】 [解析]
因为不等式组的解集为-<k≤3,
所以不等式组的整数解为-2,-1,0,1,2,3.
关于x的方程2x+k=-1的解为x=-.
因为关于x的方程2x+k=-1的解为非负数,
所以k+1≤0,解得k≤-1,
所以能使关于x的方程2x+k=-1的解为非负数的k的值为-1,-2,
所以能使关于x的方程2x+k=-1的解为非负数的概率为=.
三、解答题
17.
【答案】
解:所有可能的结果列表如下:
甲乙
1
1
2
1
偶数
偶数
奇数
2
奇数
奇数
偶数
2
奇数
奇数
偶数
由表可知,和为偶数的结果有4种,∴P(甲胜)=.
答:甲胜的概率是.
18.
【答案】
解:(1)=3.5.
答:前8次的指针所指数字的平均数为3.5.
(2)可能.
若这10次的指针所指数字的平均数不小于3.3,且不大于3.5,则所指数字之和应不小于33,且不大于35.而前8次所指数字之和为28,所以最后2次所指数字之和应不小于5,且不大于7.
第9次和第10次指针可能所指的数字如下表所示:
一共有16种等可能的结果,其中指针所指数字之和不小于5,且不大于7的结果有9种,其概率为.
19.
【答案】
解:根据题意画树状图如下:
共有16种等可能的结果,其中小明和小华查找同一位院士资料的结果有4种,所以小明和小华查找同一位院士资料的概率为=.
20.
【答案】
解:(1)
(2)画树状图如图所示.
一共有9种等可能的结果,其中能得到钝角的结果有6种,所以这个角是钝角的概率是=.
同课章节目录
