2021-2022学年北师大版九年级数学上册2.6应用一元二次方程 同步能力提升训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册2.6应用一元二次方程 同步能力提升训练(word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 167.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学上册《2.6应用一元二次方程》
同步能力提升训练(附答案)
一、填空题
1.目前以5G等为代表的战略性新兴产业蓬勃发展.某市2020年底有5G用户2万户,计划到2022年底全市5G用户数累积到达到9.5万户.设全市5G用户数年平均增长率为x,则x的值为
.
2.某校八年级组织篮球赛,若每两班之间赛一场,共进行了28场,则该校八年级有
个班级.
3.如图,某小区规划在一个长为24m、宽为10m的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若草坪部分的总面积为160m2,则小路的宽度为
m.
4.小明的叔叔家承包了一个长方形的鱼池,这个长方形鱼池的面积为40平方米,其对角线长为10米.为建栅栏,那么这个长方形鱼池的周长是
米.
5.有一张长40cm,宽30cm的长方形硬纸片(如图1),截去四个全等的小正方形之后,折成无盖的纸盒(如图2).若纸盒的底面积为600cm2,则纸盒的高为
.
6.参加一次足球联赛的每两队之间都进行两次比赛,共要比赛90场.设共有x个队参加比赛,则依题意可列方程为
.
7.如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是24cm2的有盖的长方体铁盒.则剪去的正方形的边长为
cm.
8.有一个人患了新冠肺炎,经过两轮传染后共有169人患了新冠肺炎,每轮传染中平均一个人传染了
个人.
9.如图,在一个长20m,宽10m的矩形草地内修建宽度相等的小路(阴影部分),若剩余草地(空白部分)的面积171m2,则小路的宽度为
m.
10.如果一个矩形的一边长是某个正方形边长的2倍,另一边长比该正方形边长少1厘米,且矩形的面积比该正方形的面积大8平方厘米,那么该正方形的边长是
厘米.
11.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.当y=﹣1时,n=
.
12.一个凸多边形共有9条对角线,则这个多边形的边数是
.
13.如图,邻边不等的长方形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是5m.EF处开一门,宽度为1m,若长方形ABCD的面积为4m2,则AB的长度是
m(可利用的围墙长度超过4m).
如图Rt△ABC中,∠A=90°,AB=6,AC=8,动点P从点A开始以每秒1个单位长度的速度沿边AC向点C运动,同时动点Q从点C开始,以每秒2个单位长度的速度沿C→B→A的折线在CB、BA边上向点A运动,当P点到达C点时,两点同时停止运动,连接PQ.在运动过程中(Q点在C、B、A三点除外),线段PQ将△ABC分成一个三角形和一个四边形,若四边形的面积为三角形面积的2倍,则运动的时间为
秒.
二、解答题
15.随着“共享经济”的概念迅速普及,共享汽车也进入了人们的视野,某共享汽车租赁公司年初在某地投放了一批共享汽车,全天包车的租金定为每辆120元.据统计,三月份的全天包车数为25次,在租金不变的基础上,四、五月的全天包车数持续走高,五月份的全天包车数达到64次.
(1)若从三月份到五月份的全天包车数月平均增长率不变,求全天包车数的月平均增长率;
(2)从六月份起,该公司决定降低租金,经调查发现,租金每降价a元,全天包车数增加1.6a次,当租金降价多少元时,公司将获利8800元?
16.如图是一张长24cm,宽12cm的矩形铁皮,将其剪去一个小正方形和两个矩形,剩余部分(阴影部分)恰好可制成一个有盖的长方体铁盒.
(1)a=
;
(2)若铁盒底面积是80cm2,求剪去的小正方形边长.
17.利好家电商场销售某种品牌的空调扇:据市场调查:每台空调扇按480元销售时,每天可销售160台;若销售单价每降低1元,每天可多销售2台,已知每台空调扇的成本价为360元.
(1)根据题意完成下列表格:
每台降价(元)
每台售价(元)
每台利润(元)
销售数量(元)
每天利润(元)
10
470
110
x
(2)该品牌的空调扇的销售单价为多少元时,利好商场每天可获利18200元?
18.7至9月份“铁岭莲花湿地公园”迎来了荷花的盛放期,来此观赏荷花的游客络绎不绝,由此带动了湿地周边的餐饮服务业的发展;“听荷坊”宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
x(元)
180
260
280
300
y(间)
100
60
50
40
(1)请求出y与x的函数关系式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元,每日空置的客房需支出各种费用60元;当房价为多少元时,宾馆当日可获利8450元?
19.为了满足市场上的口罩需求,某厂购进A、B两种口罩生产设备若干台,已知购买A种口罩生产设备共花费360万元,购买B种口罩生产设备共花费480万元.购买的两种设备数量相同,且两种口罩生产设备的单价和为140万元.
(1)求A、B两种口罩生产设备的单价;
(2)已知该厂每生产一盒口罩需要各种成本40元,如果按照每盒50元的价格进行销售,每天可以售出500盒.后来经过市场调查发现,若每盒口罩涨价1元,则口罩的销量每天减少20盒,要保证每天销售口罩盈利6000元,且规避过高涨价风险,则每盒口罩可涨价多少元?
20.某商场销售一批衬衫,每件成本为50元,如果按每件60元出售,可销售800件;如果每件提价5元出售,其销售量就减少100件.如果商场销售这批衬衫要获利润12000元,又使顾客获得更多的优惠,那么这种衬衫应提价多少元?
(1)设这种衬衫应提价x元,则这种衬衫的销售价为
元,销售量为
件.
(2)列方程并完成本题的解答.
21.如图,在一块长AB=80米,宽AD=60米的矩形空地ABCD上修建两条水平和一条铅直道路,已知水平道路和铅直道路的宽之比为3:4,剩余空地面积为3456平方米.
(1)请你计算水平和铅直道路的宽分别是多少米.
(2)若将其中一条水平道路改为铅直道路,宽度也随之改变为铅直道路的宽度,也能保证剩余空地面积为3456平方米,你能说明理由吗?
22.列方程(组)解应用题
某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
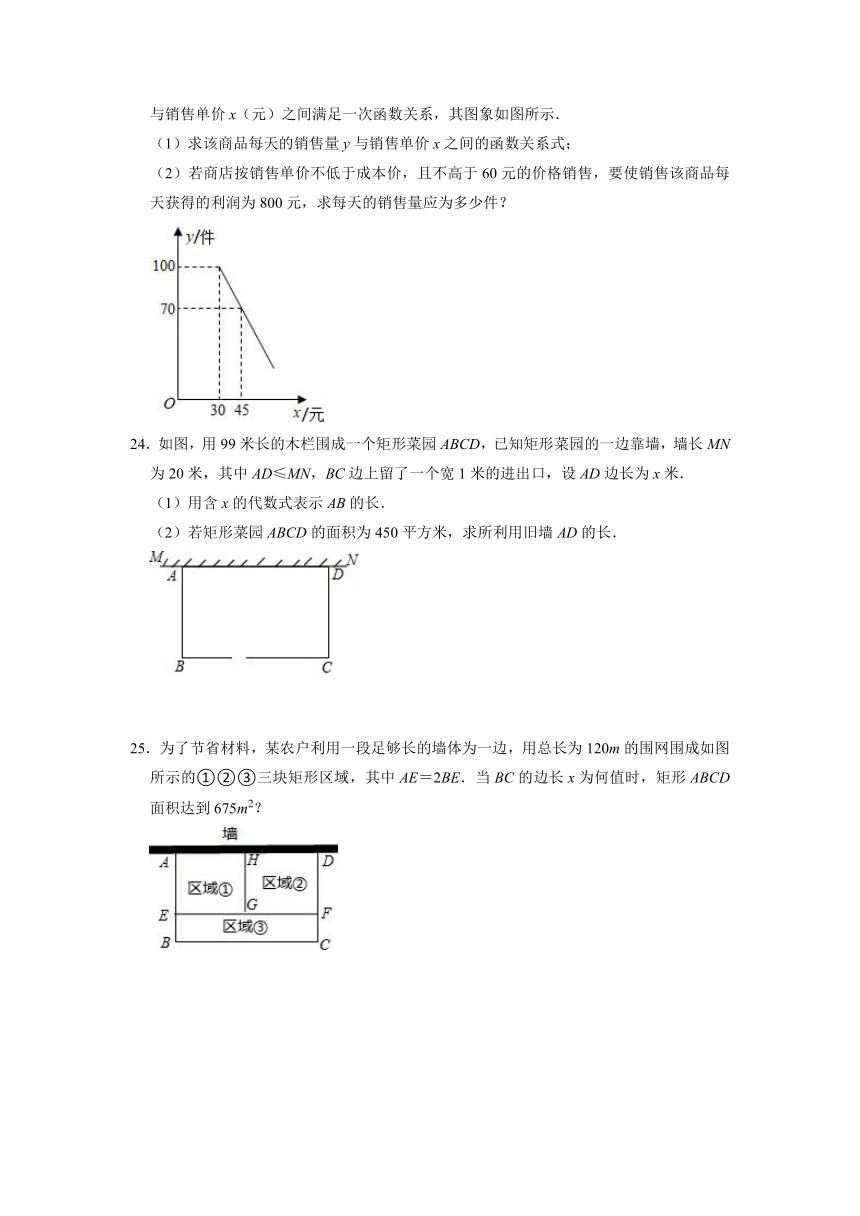
23.某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量y与销售单价x之间的函数关系式;
(2)若商店按销售单价不低于成本价,且不高于60元的价格销售,要使销售该商品每天获得的利润为800元,求每天的销售量应为多少件?
24.如图,用99米长的木栏围成一个矩形菜园ABCD,已知矩形菜园的一边靠墙,墙长MN为20米,其中AD≤MN,BC边上留了一个宽1米的进出口,设AD边长为x米.
(1)用含x的代数式表示AB的长.
(2)若矩形菜园ABCD的面积为450平方米,求所利用旧墙AD的长.
25.为了节省材料,某农户利用一段足够长的墙体为一边,用总长为120m的围网围成如图所示的①②③三块矩形区域,其中AE=2BE.当BC的边长x为何值时,矩形ABCD面积达到675m2?
参考答案
1.解:设全市5G用户数年平均增长率为x,
依题意,得:2+2(1+x)+2(1+x)2=9.5,
整理得x2+3x﹣1.75=0,
解得:x1=0.5=50%,x2=﹣3.5(不合题意,舍去).
故答案为:50%.
2.解:设八年级有x个班,
依题意得:x(x﹣1)=28,
整理得:x2﹣x﹣56=0,
解得:x1=8,x2=﹣7(不合题意,舍去).
则该校八年级有8个班级.
故答案为:8.
3.解:如图,设修建的小路宽应为x米,
则新的草坪面积等于矩形DEFG的面积,
即得到方程:(24﹣2x)×(10﹣x)=160,
整理得:x2﹣22x+40=0,解得x=20或x=2.
但x=20不合题意,舍去,
所以修建的小路宽应为2米.
故答案为:2.
4.解:设矩形的长是a,宽是b,
根据题意,得:
,
②+①×2,得(a+b)2=180,即a+b=6,
∴2(a+b)=6×2=12(米).
答:矩形的周长是12米.
故答案为:12.
5.解:设纸盒的高为xcm,则纸盒的底面长为(40﹣2x)cm,宽为(30﹣2x)cm,可列方程:
(40﹣2x)(30﹣2x)=600,
解得:x1=5,x2=30(舍去),
∴纸盒的高为5cm,
故答案为:5cm.
6.解:设有x个队参赛,
x(x﹣1)=90.
故答案为:x(x﹣1)=90.
7.解:设底面长为acm,宽为bcm,正方形的边长为xcm,根据题意得:
,
解得a=10﹣2x,b=6﹣x,
代入ab=24中,得:
(10﹣2x)(6﹣x)=24,
整理得:x2﹣11x+18=0,
解得x=2或x=9(舍去),
答:剪去的正方形的边长为2cm.
故答案为:2.
8.解:设每轮传染中平均一个人传染了x个人,根据题意,得
x+1+(x+1)x=169
x=12或x=﹣14(舍去).
答:每轮传染中平均一个人传染了12个人.
故答案为:12.
9.解:设小路的宽度为xm,根据题意列方程得
(20﹣x)(10﹣x)=171,
整理得:x2﹣30x+29=0,
解得:x1=1,x2=29(不合题意,舍去).
故小路的宽度为1m.
故答案为:1.
10.解:设正方形的边长为x厘米,则矩形的一边长为2x厘米,另一边长为(x﹣1)厘米,
由题意得,2x(x﹣1)﹣x2=8,
整理得,x2﹣2x﹣8=0,
解得,x1=﹣2(舍去),x2=4,
故答案为:4.
11.解:根据题意,可得:x2+2x=m,2x+3=n,m+n=y,
∵y=﹣1,
∴x2+2x+2x+3=﹣1,
∴x2+4x+4=0,
∴(x+2)2=0,
∴x+2=0,
解得x=﹣2,
∴n=2x+3=2×(﹣2)+3=﹣1.
故答案为:﹣1.
12.解:设多边形有n条边,
则=9,
解得n1=6,n2=﹣3(舍去),
故这个多边形的边数为6.
13.解:设AB长为xm,则BC长为(5+1﹣2x)m.
依题意得x(5+1﹣2x)=4,
整理得x2﹣3x+2=0,
解方程得x1=1,x2=2.
所以当x=1时,6﹣2x=4;
当x=2时,6﹣2x=2(舍去).
答:AB的长为1m.
故答案为:1.
14.解:在Rt△ABC中,∠A=90°,AB=6,AC=8,
∴BC=10
设运动的时间为t,则AP=t,点Q所走的路程为2t,
1)当点Q在BC线段上运动时,0<t<5,
如图所示,过点Q作QG⊥AC,交AC于点G,
则sinC==
∴QG=×2t=
∵S△ABC=6×8÷2=24
若四边形的面积为三角形面积的2倍,则S△PQC=24×=8
∴(8﹣t)×÷2=8
化简得3t2﹣24t+40=0
解得t1=4﹣,t2=4+(舍)
2)当点Q在BA线段上运动时,5<t<8,
如图所示,
S△APQ=AP?AQ=t(10+6﹣2t)=8
化简得:t2﹣8t+8=0
解得t3=4﹣2(舍),t4=4+2.
故答案为:4﹣或4+2.
15.解:(1)设全天包车数的月平均增长率为x,
根据题意可得:25(1+x)2=64,
解得:x1=0.6=60%,x2=﹣2.6(不合题意舍去),
答:全天包车数的月平均增长率为60%;
(2)根据题意可得:(120﹣a)(64+1.6a)=8800,
化简得:a2﹣80a+700=0,
解得:a1=10,a2=70.
答:当租金降价10元或70元时,公司将获利8800元.
16.解:(1)设底面长为mcm,宽为ncm,正方形的边长为xcm,根据题意得:
,
由②③得2a=24,解得a=12(cm),
故答案为:12cm;
(2)根据题意,得
mn=80,
由,得
由①得,n=12﹣2x,
把a=12代入②得m=12﹣x,
再把m和n代入mn=80中,得
(12﹣x)(12﹣2x)=80,
解得x=2或x=16(舍去).
答:剪去的小正方形边长为2cm.
17.解:(1)当每台降价10元时,销售数量为160+2×10=180(台),每天的利润为110×180=19800(元);
当每台降价x元时,每台售价为(480﹣x)元,每台的利润为480﹣x﹣360=(120﹣x)元,销售数量为(160+2x)台,每天的利润为(120﹣x)(160+2x)=(﹣2x2+80x+19200)元.
故答案为:180;19800;480﹣x;120﹣x;160+2x;﹣2x2+80x+19200.
(2)依题意,得:﹣2x2+80x+19200=18200,
整理,得:x2﹣40x﹣500=0,
解得:x1=50,x2=﹣10(不合题意,舍去),
当x=50时,480﹣x=430.
答:该品牌的空调扇的销售单价为430元时,利好商场每天可获利18200元.
18.解:(1)设y与x的函数关系式为y=kx+b,
把(180,100),(260,60)分别代入解析式,得
,
解得,
所以y与x的函数关系式为y=﹣x+190(180≤x≤300);
(2)由题意可知:
(x﹣100)(x+190)﹣60[100﹣(﹣x+190)]=8450,
整理得:x2﹣420x+44100=0,
解得x1=x2=210.
答:当房价为210元时,宾馆当日可获利8450元,
19.解:(1)设A种口罩生产设备的单价为x万元,则B种口罩生产设备的单价为(140﹣x)万元,依题意有
=,
解得x=60,
经检验,x=60是原方程的解,且符合题意,
则140﹣x=140﹣60=80.
答:A种口罩生产设备的单价为60万元,则B种口罩生产设备的单价为80万元;
(2)设每盒口罩可涨价m元,依题意有
(50﹣40+m)(500﹣20m)=6000,
解得m1=5,m2=10(舍去).
故每盒口罩可涨价5元.
20.解:(1)设这种衬衫应提价x元,则这种衬衫的销售价为(60+x)元,
销售量为(800﹣x)=(800﹣20x)件.
故答案为(60+x)、(800﹣20x).
(2)根据(1)得:
(60+x﹣50)(800﹣20x)=12000
整理,得x2﹣30x+200=0
解得:x1=10,x2=20.
为使顾客获得更多的优惠,
所以x=10,60+x=70,800﹣20x=600.
答:这种衬衫应提价10元,则这种衬衫的销售价为70元,销售量为600件.
21.解:(1)设水平道路和铅直道路的宽分别为3x米和4x米,由题意有
(80﹣4x)(60﹣2×3x)=3456,
解得x1=28(舍去),x2=2.
答:水平道路的宽为6米,铅直道路的宽为8米.
(2)每条水平道路的面积为80×6=480(平方米),
每条铅直道路的面积为60×8=480(平方米),
∴将水平道路改为铅直道路,也能保证剩余空地面积为3456平方米.
22.解:设茶园垂直于墙的一边长为xm,则另一边的长度为(69+1﹣2x)m,根据题意,得
x(69+1﹣2x)=600,
整理,得
x2﹣35x+300=0,
解得x1=15,x2=20,
当x=15时,70﹣2x=40>35,不符合题意舍去;
当x=20时,70﹣2x=30,符合题意.
答:这个茶园的长和宽分别为30m、20m.
23.解:(1)设y与销售单价x之间的函数关系式为:y=kx+b,
将点(30,100)、(45,70)代入一次函数表达式得:,
解得:,
故函数的表达式为:y=﹣2x+160;
(2)由题意得:(x﹣30)(﹣2x+160)=800,
解得:x1=40,x2=70,
∵销售单价不低于成本价,且不高于60元,
∴x=40,
∴y=﹣2x+160=﹣2×40+160=80(件).
答:每天的销售量应为80件.
24.解:(1)AB==(米);
(2)依题意有
x?=450,
解得x1=10,x2=90.
∵10<20,90>20,
∴x=10.
故所利用旧墙AD的长为10米.
25.解:设BE=a,则AE=2a,AB=3a.
根据题意得:2x+8a=120,
∴a=15﹣x.
∴AB=3a=45﹣x.
∴x(45﹣x)=675.
解得:x1=x2=30m.
∴当BC=30m时,矩形ABCD面积为675m2
同步能力提升训练(附答案)
一、填空题
1.目前以5G等为代表的战略性新兴产业蓬勃发展.某市2020年底有5G用户2万户,计划到2022年底全市5G用户数累积到达到9.5万户.设全市5G用户数年平均增长率为x,则x的值为
.
2.某校八年级组织篮球赛,若每两班之间赛一场,共进行了28场,则该校八年级有
个班级.
3.如图,某小区规划在一个长为24m、宽为10m的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若草坪部分的总面积为160m2,则小路的宽度为
m.
4.小明的叔叔家承包了一个长方形的鱼池,这个长方形鱼池的面积为40平方米,其对角线长为10米.为建栅栏,那么这个长方形鱼池的周长是
米.
5.有一张长40cm,宽30cm的长方形硬纸片(如图1),截去四个全等的小正方形之后,折成无盖的纸盒(如图2).若纸盒的底面积为600cm2,则纸盒的高为
.
6.参加一次足球联赛的每两队之间都进行两次比赛,共要比赛90场.设共有x个队参加比赛,则依题意可列方程为
.
7.如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是24cm2的有盖的长方体铁盒.则剪去的正方形的边长为
cm.
8.有一个人患了新冠肺炎,经过两轮传染后共有169人患了新冠肺炎,每轮传染中平均一个人传染了
个人.
9.如图,在一个长20m,宽10m的矩形草地内修建宽度相等的小路(阴影部分),若剩余草地(空白部分)的面积171m2,则小路的宽度为
m.
10.如果一个矩形的一边长是某个正方形边长的2倍,另一边长比该正方形边长少1厘米,且矩形的面积比该正方形的面积大8平方厘米,那么该正方形的边长是
厘米.
11.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.当y=﹣1时,n=
.
12.一个凸多边形共有9条对角线,则这个多边形的边数是
.
13.如图,邻边不等的长方形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是5m.EF处开一门,宽度为1m,若长方形ABCD的面积为4m2,则AB的长度是
m(可利用的围墙长度超过4m).
如图Rt△ABC中,∠A=90°,AB=6,AC=8,动点P从点A开始以每秒1个单位长度的速度沿边AC向点C运动,同时动点Q从点C开始,以每秒2个单位长度的速度沿C→B→A的折线在CB、BA边上向点A运动,当P点到达C点时,两点同时停止运动,连接PQ.在运动过程中(Q点在C、B、A三点除外),线段PQ将△ABC分成一个三角形和一个四边形,若四边形的面积为三角形面积的2倍,则运动的时间为
秒.
二、解答题
15.随着“共享经济”的概念迅速普及,共享汽车也进入了人们的视野,某共享汽车租赁公司年初在某地投放了一批共享汽车,全天包车的租金定为每辆120元.据统计,三月份的全天包车数为25次,在租金不变的基础上,四、五月的全天包车数持续走高,五月份的全天包车数达到64次.
(1)若从三月份到五月份的全天包车数月平均增长率不变,求全天包车数的月平均增长率;
(2)从六月份起,该公司决定降低租金,经调查发现,租金每降价a元,全天包车数增加1.6a次,当租金降价多少元时,公司将获利8800元?
16.如图是一张长24cm,宽12cm的矩形铁皮,将其剪去一个小正方形和两个矩形,剩余部分(阴影部分)恰好可制成一个有盖的长方体铁盒.
(1)a=
;
(2)若铁盒底面积是80cm2,求剪去的小正方形边长.
17.利好家电商场销售某种品牌的空调扇:据市场调查:每台空调扇按480元销售时,每天可销售160台;若销售单价每降低1元,每天可多销售2台,已知每台空调扇的成本价为360元.
(1)根据题意完成下列表格:
每台降价(元)
每台售价(元)
每台利润(元)
销售数量(元)
每天利润(元)
10
470
110
x
(2)该品牌的空调扇的销售单价为多少元时,利好商场每天可获利18200元?
18.7至9月份“铁岭莲花湿地公园”迎来了荷花的盛放期,来此观赏荷花的游客络绎不绝,由此带动了湿地周边的餐饮服务业的发展;“听荷坊”宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
x(元)
180
260
280
300
y(间)
100
60
50
40
(1)请求出y与x的函数关系式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元,每日空置的客房需支出各种费用60元;当房价为多少元时,宾馆当日可获利8450元?
19.为了满足市场上的口罩需求,某厂购进A、B两种口罩生产设备若干台,已知购买A种口罩生产设备共花费360万元,购买B种口罩生产设备共花费480万元.购买的两种设备数量相同,且两种口罩生产设备的单价和为140万元.
(1)求A、B两种口罩生产设备的单价;
(2)已知该厂每生产一盒口罩需要各种成本40元,如果按照每盒50元的价格进行销售,每天可以售出500盒.后来经过市场调查发现,若每盒口罩涨价1元,则口罩的销量每天减少20盒,要保证每天销售口罩盈利6000元,且规避过高涨价风险,则每盒口罩可涨价多少元?
20.某商场销售一批衬衫,每件成本为50元,如果按每件60元出售,可销售800件;如果每件提价5元出售,其销售量就减少100件.如果商场销售这批衬衫要获利润12000元,又使顾客获得更多的优惠,那么这种衬衫应提价多少元?
(1)设这种衬衫应提价x元,则这种衬衫的销售价为
元,销售量为
件.
(2)列方程并完成本题的解答.
21.如图,在一块长AB=80米,宽AD=60米的矩形空地ABCD上修建两条水平和一条铅直道路,已知水平道路和铅直道路的宽之比为3:4,剩余空地面积为3456平方米.
(1)请你计算水平和铅直道路的宽分别是多少米.
(2)若将其中一条水平道路改为铅直道路,宽度也随之改变为铅直道路的宽度,也能保证剩余空地面积为3456平方米,你能说明理由吗?
22.列方程(组)解应用题
某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
23.某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量y与销售单价x之间的函数关系式;
(2)若商店按销售单价不低于成本价,且不高于60元的价格销售,要使销售该商品每天获得的利润为800元,求每天的销售量应为多少件?
24.如图,用99米长的木栏围成一个矩形菜园ABCD,已知矩形菜园的一边靠墙,墙长MN为20米,其中AD≤MN,BC边上留了一个宽1米的进出口,设AD边长为x米.
(1)用含x的代数式表示AB的长.
(2)若矩形菜园ABCD的面积为450平方米,求所利用旧墙AD的长.
25.为了节省材料,某农户利用一段足够长的墙体为一边,用总长为120m的围网围成如图所示的①②③三块矩形区域,其中AE=2BE.当BC的边长x为何值时,矩形ABCD面积达到675m2?
参考答案
1.解:设全市5G用户数年平均增长率为x,
依题意,得:2+2(1+x)+2(1+x)2=9.5,
整理得x2+3x﹣1.75=0,
解得:x1=0.5=50%,x2=﹣3.5(不合题意,舍去).
故答案为:50%.
2.解:设八年级有x个班,
依题意得:x(x﹣1)=28,
整理得:x2﹣x﹣56=0,
解得:x1=8,x2=﹣7(不合题意,舍去).
则该校八年级有8个班级.
故答案为:8.
3.解:如图,设修建的小路宽应为x米,
则新的草坪面积等于矩形DEFG的面积,
即得到方程:(24﹣2x)×(10﹣x)=160,
整理得:x2﹣22x+40=0,解得x=20或x=2.
但x=20不合题意,舍去,
所以修建的小路宽应为2米.
故答案为:2.
4.解:设矩形的长是a,宽是b,
根据题意,得:
,
②+①×2,得(a+b)2=180,即a+b=6,
∴2(a+b)=6×2=12(米).
答:矩形的周长是12米.
故答案为:12.
5.解:设纸盒的高为xcm,则纸盒的底面长为(40﹣2x)cm,宽为(30﹣2x)cm,可列方程:
(40﹣2x)(30﹣2x)=600,
解得:x1=5,x2=30(舍去),
∴纸盒的高为5cm,
故答案为:5cm.
6.解:设有x个队参赛,
x(x﹣1)=90.
故答案为:x(x﹣1)=90.
7.解:设底面长为acm,宽为bcm,正方形的边长为xcm,根据题意得:
,
解得a=10﹣2x,b=6﹣x,
代入ab=24中,得:
(10﹣2x)(6﹣x)=24,
整理得:x2﹣11x+18=0,
解得x=2或x=9(舍去),
答:剪去的正方形的边长为2cm.
故答案为:2.
8.解:设每轮传染中平均一个人传染了x个人,根据题意,得
x+1+(x+1)x=169
x=12或x=﹣14(舍去).
答:每轮传染中平均一个人传染了12个人.
故答案为:12.
9.解:设小路的宽度为xm,根据题意列方程得
(20﹣x)(10﹣x)=171,
整理得:x2﹣30x+29=0,
解得:x1=1,x2=29(不合题意,舍去).
故小路的宽度为1m.
故答案为:1.
10.解:设正方形的边长为x厘米,则矩形的一边长为2x厘米,另一边长为(x﹣1)厘米,
由题意得,2x(x﹣1)﹣x2=8,
整理得,x2﹣2x﹣8=0,
解得,x1=﹣2(舍去),x2=4,
故答案为:4.
11.解:根据题意,可得:x2+2x=m,2x+3=n,m+n=y,
∵y=﹣1,
∴x2+2x+2x+3=﹣1,
∴x2+4x+4=0,
∴(x+2)2=0,
∴x+2=0,
解得x=﹣2,
∴n=2x+3=2×(﹣2)+3=﹣1.
故答案为:﹣1.
12.解:设多边形有n条边,
则=9,
解得n1=6,n2=﹣3(舍去),
故这个多边形的边数为6.
13.解:设AB长为xm,则BC长为(5+1﹣2x)m.
依题意得x(5+1﹣2x)=4,
整理得x2﹣3x+2=0,
解方程得x1=1,x2=2.
所以当x=1时,6﹣2x=4;
当x=2时,6﹣2x=2(舍去).
答:AB的长为1m.
故答案为:1.
14.解:在Rt△ABC中,∠A=90°,AB=6,AC=8,
∴BC=10
设运动的时间为t,则AP=t,点Q所走的路程为2t,
1)当点Q在BC线段上运动时,0<t<5,
如图所示,过点Q作QG⊥AC,交AC于点G,
则sinC==
∴QG=×2t=
∵S△ABC=6×8÷2=24
若四边形的面积为三角形面积的2倍,则S△PQC=24×=8
∴(8﹣t)×÷2=8
化简得3t2﹣24t+40=0
解得t1=4﹣,t2=4+(舍)
2)当点Q在BA线段上运动时,5<t<8,
如图所示,
S△APQ=AP?AQ=t(10+6﹣2t)=8
化简得:t2﹣8t+8=0
解得t3=4﹣2(舍),t4=4+2.
故答案为:4﹣或4+2.
15.解:(1)设全天包车数的月平均增长率为x,
根据题意可得:25(1+x)2=64,
解得:x1=0.6=60%,x2=﹣2.6(不合题意舍去),
答:全天包车数的月平均增长率为60%;
(2)根据题意可得:(120﹣a)(64+1.6a)=8800,
化简得:a2﹣80a+700=0,
解得:a1=10,a2=70.
答:当租金降价10元或70元时,公司将获利8800元.
16.解:(1)设底面长为mcm,宽为ncm,正方形的边长为xcm,根据题意得:
,
由②③得2a=24,解得a=12(cm),
故答案为:12cm;
(2)根据题意,得
mn=80,
由,得
由①得,n=12﹣2x,
把a=12代入②得m=12﹣x,
再把m和n代入mn=80中,得
(12﹣x)(12﹣2x)=80,
解得x=2或x=16(舍去).
答:剪去的小正方形边长为2cm.
17.解:(1)当每台降价10元时,销售数量为160+2×10=180(台),每天的利润为110×180=19800(元);
当每台降价x元时,每台售价为(480﹣x)元,每台的利润为480﹣x﹣360=(120﹣x)元,销售数量为(160+2x)台,每天的利润为(120﹣x)(160+2x)=(﹣2x2+80x+19200)元.
故答案为:180;19800;480﹣x;120﹣x;160+2x;﹣2x2+80x+19200.
(2)依题意,得:﹣2x2+80x+19200=18200,
整理,得:x2﹣40x﹣500=0,
解得:x1=50,x2=﹣10(不合题意,舍去),
当x=50时,480﹣x=430.
答:该品牌的空调扇的销售单价为430元时,利好商场每天可获利18200元.
18.解:(1)设y与x的函数关系式为y=kx+b,
把(180,100),(260,60)分别代入解析式,得
,
解得,
所以y与x的函数关系式为y=﹣x+190(180≤x≤300);
(2)由题意可知:
(x﹣100)(x+190)﹣60[100﹣(﹣x+190)]=8450,
整理得:x2﹣420x+44100=0,
解得x1=x2=210.
答:当房价为210元时,宾馆当日可获利8450元,
19.解:(1)设A种口罩生产设备的单价为x万元,则B种口罩生产设备的单价为(140﹣x)万元,依题意有
=,
解得x=60,
经检验,x=60是原方程的解,且符合题意,
则140﹣x=140﹣60=80.
答:A种口罩生产设备的单价为60万元,则B种口罩生产设备的单价为80万元;
(2)设每盒口罩可涨价m元,依题意有
(50﹣40+m)(500﹣20m)=6000,
解得m1=5,m2=10(舍去).
故每盒口罩可涨价5元.
20.解:(1)设这种衬衫应提价x元,则这种衬衫的销售价为(60+x)元,
销售量为(800﹣x)=(800﹣20x)件.
故答案为(60+x)、(800﹣20x).
(2)根据(1)得:
(60+x﹣50)(800﹣20x)=12000
整理,得x2﹣30x+200=0
解得:x1=10,x2=20.
为使顾客获得更多的优惠,
所以x=10,60+x=70,800﹣20x=600.
答:这种衬衫应提价10元,则这种衬衫的销售价为70元,销售量为600件.
21.解:(1)设水平道路和铅直道路的宽分别为3x米和4x米,由题意有
(80﹣4x)(60﹣2×3x)=3456,
解得x1=28(舍去),x2=2.
答:水平道路的宽为6米,铅直道路的宽为8米.
(2)每条水平道路的面积为80×6=480(平方米),
每条铅直道路的面积为60×8=480(平方米),
∴将水平道路改为铅直道路,也能保证剩余空地面积为3456平方米.
22.解:设茶园垂直于墙的一边长为xm,则另一边的长度为(69+1﹣2x)m,根据题意,得
x(69+1﹣2x)=600,
整理,得
x2﹣35x+300=0,
解得x1=15,x2=20,
当x=15时,70﹣2x=40>35,不符合题意舍去;
当x=20时,70﹣2x=30,符合题意.
答:这个茶园的长和宽分别为30m、20m.
23.解:(1)设y与销售单价x之间的函数关系式为:y=kx+b,
将点(30,100)、(45,70)代入一次函数表达式得:,
解得:,
故函数的表达式为:y=﹣2x+160;
(2)由题意得:(x﹣30)(﹣2x+160)=800,
解得:x1=40,x2=70,
∵销售单价不低于成本价,且不高于60元,
∴x=40,
∴y=﹣2x+160=﹣2×40+160=80(件).
答:每天的销售量应为80件.
24.解:(1)AB==(米);
(2)依题意有
x?=450,
解得x1=10,x2=90.
∵10<20,90>20,
∴x=10.
故所利用旧墙AD的长为10米.
25.解:设BE=a,则AE=2a,AB=3a.
根据题意得:2x+8a=120,
∴a=15﹣x.
∴AB=3a=45﹣x.
∴x(45﹣x)=675.
解得:x1=x2=30m.
∴当BC=30m时,矩形ABCD面积为675m2
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
