2021-2022学年九年级数学苏科版上册2.2圆的对称性同步能力提升训练(word版、含答案)
文档属性
| 名称 | 2021-2022学年九年级数学苏科版上册2.2圆的对称性同步能力提升训练(word版、含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 431.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 15:38:18 | ||
图片预览




文档简介
2021-2022学年苏科版九年级数学上册《2.2圆的对称性》同步能力提升训练(附答案)
一、选择题
1.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米
B.(4﹣)米
C.2米
D.(4+)米
2.如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )
A.9.6
B.4
C.5
D.10
3.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A.1.0厘米/分
B.0.8厘米/分
C.1.2厘米/分
D.1.4厘米/分
4.往水平放置的半径为13cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=24cm,则水的最大深度为( )
A.5cm
B.8cm
C.10cm
D.12cm
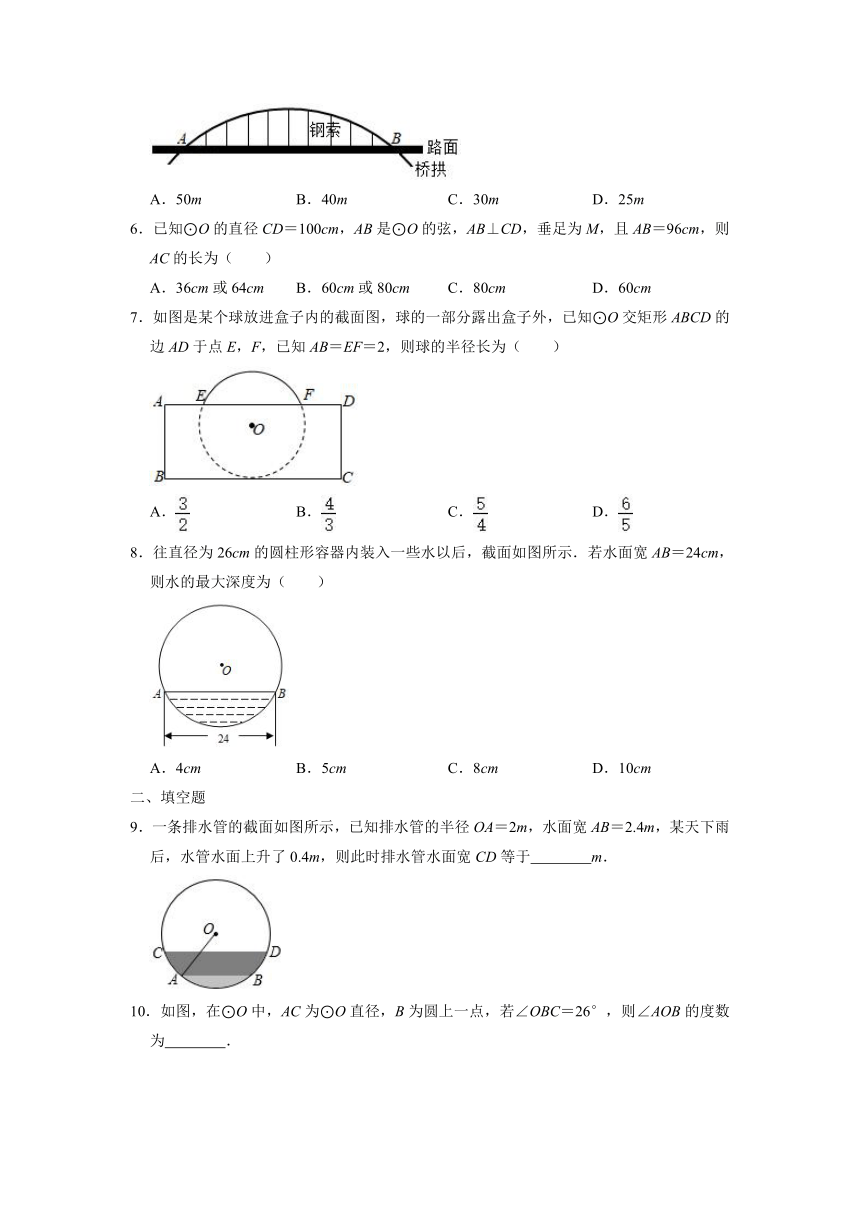
5.如图,拱桥可以近似地看作直径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为150m,那么这些钢索中最长的一根的长度为( )
A.50m
B.40m
C.30m
D.25m
6.已知⊙O的直径CD=100cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=96cm,则AC的长为( )
A.36cm或64cm
B.60cm或80cm
C.80cm
D.60cm
7.如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为( )
A.
B.
C.
D.
8.往直径为26cm的圆柱形容器内装入一些水以后,截面如图所示.若水面宽AB=24cm,则水的最大深度为( )
A.4cm
B.5cm
C.8cm
D.10cm
二、填空题
9.一条排水管的截面如图所示,已知排水管的半径OA=2m,水面宽AB=2.4m,某天下雨后,水管水面上升了0.4m,则此时排水管水面宽CD等于
m.
10.如图,在⊙O中,AC为⊙O直径,B为圆上一点,若∠OBC=26°,则∠AOB的度数为
.
11.如图,矩形ABCD中,AB=6,以点D为圆心,CD长为半径的圆弧与以BC为直径的半圆O相交于点E,若的度数为60°,则直径BC长为
.
12.如图,在平面直角坐标系中,半径为3的⊙O与y轴的负半轴交于点A,点B是⊙O上移动点,点C为弦AB的中点,直线与x轴、y轴分别相交于点D、E,则△CDE面积的最小值为
.
三、解答题
13.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,BC=3.
(1)求AB的长;
(2)求⊙O的半径.
14.已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点.
(1)求圆心O到AP的距离;
(2)求弦EF的长.
15.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
16.如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:AC=BD;
(2)连接OA、OC,若OA=6,OC=4,∠OCD=60°,求AC的长.
17.如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
18.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),求该圆材的直径.
19.如图1,点P表示我国古代水车的一个盛水筒.如图2,当水车工作时,盛水筒的运行路径是以轴心O为圆心,5m为半径的圆.若⊙O被水面截得的弦AB长为8m,求水车工作时,盛水筒在水面以下的最大深度.
20.某地有一座圆弧形拱桥,所在圆的圆心为点O,桥下水面宽度AB为7.2m,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4m(如图).现有一艘宽3m、船舱顶部高出水面AB2m的货船要经过这座拱桥,此货船能否顺利通过这座拱桥?
参考答案
1.解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
2.解:∵OE⊥AC于点E.
∴AE=EC.
∵OE=3,OB=5.
∴AE=.
∴AC=8.
∵∠A=∠A,∠AEO=∠AFC.
∴.
∵CD⊥AB.
∴CD=2CF==9.6.
故选:A.
3.解:设“图上”圆的圆心为O,连接OA,过点O作OD⊥AB于D,如图所示:
∵AB=16厘米,
∴AD=AB=8(厘米),
∵OA=10厘米,
∴OD===6(厘米),
∴海平线以下部分的高度=OA+OD=10+6=16(厘米),
∵太阳从所处位置到完全跳出海平面的时间为16分钟,
∴“图上”太阳升起的速度=16÷16=1.0(厘米/分),
故选:A.
4.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:B.
5.解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=×250=125(m),AC=BC=AB=×150=75(m),
∴OC===100(m),
∴CD=OD﹣OC=125﹣100=25(m),
即这些钢索中最长的一根为25m,
故选:D.
6.解:连接AC,AO,
∵⊙O的直径CD=100cm,AB⊥CD,AB=96cm,
∴AM=AB=×96=48(cm),OD=OC=50(cm),
如图1,∵OA=50cm,AM=48cm,CD⊥AB,
∴OM===14(cm),
∴CM=OC+OM=50+14=64(cm),
∴AC===80(cm);
如图2,同理可得,OM=14cm,
∵OC=50cm,
∴MC=50﹣14=36(cm),
在Rt△AMC中,AC==60(cm);
综上所述,AC的长为80cm或60cm,
故选:B.
7.解:由题意得:⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧于点H、I,连接OF,如图所示:
∵四边形ABCD是矩形,
∴AD∥BC,
∵IG⊥BC,
∴IG⊥AD,
∴FH=EF=1,
设⊙O的半径为r,则OH=2﹣r,
在Rt△OFH中,由勾股定理得:r2﹣(2﹣r)2=12,
解得:r=,
即球的半径长为,
故选:C.
8.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵⊙O的直径为26cm,
∴OB=OC=13(cm),
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:C.
9.解:过O作OE⊥AB于E,交CD于F,连接OC,如图所示:
则AE=BE=AB=1.2(m),OF⊥CD,
∴CF=DF=CD,
∴OE===1.6(m),
∵水管水面上升了0.4m,
∴OF=OE﹣EF=1.6﹣0.4=1.2(m),
∴CF===1.6(m),
∴CD=2CF=3.2(m)
故答案为:3.2.
10.解:∵∠OBC=26°,OB=OC,
∴∠C=∠OBC=26°,
∴∠AOB=2∠C=52°,
故答案为:52°.
11.解:如图,连接BE,EC.
∵BC是直径,
∴∠BEC=90°,
∵的度数=60°,
∴∠BCE=×60°=30°,
∵四边形ABCD是矩形,
∴AB=CD=6,∠DCB=90°,
∴∠DCE=90°﹣30°=60°,
∵DE=DC,
∴△DEC是等边三角形,
∴EC=CD=6,
∴BC=4.
故答案为:.
12.解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.
∵AC=CB,AM=OM,
∴MC=OB=,
∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.
∵直线y=﹣x﹣5与x轴、y轴分别交于点D、E,
∴D(﹣12,0),E(0,﹣5),
∴OD=12,OE=5,
∴DE===13,
∵∠MDN=∠ODE,∠MND=∠DOE,
∴MN=,
当点C与C′重合时,△C′DE的面积最小,△C′DE的面积最小值=×13×(﹣)=,
故答案为:.
13.解:(1)连接AC,如图,
∵CD⊥AB,
∴AF=BF,即CD垂直平分AB,
∴CA=CB=3,
∵AO⊥BC,
∴CE=BE,即AE垂直平分BC,
∴AB=AC=3;
(2)∵AB=AC=BC,
∴△ABC为等边三角形,
∴∠BAC=60°,
∴AE⊥BC,
∴AE平分∠BAC,即∠OAF=30°,
在Rt△OAF中,∵OF=AF=×=,
∴OA=2OF=,
即⊙O的半径为.
14.解:(1)过O点作OH⊥EF于H,如图,
∵DB=10,
∴OD=5,
∴OA=AD+OD=3+5=8,
在Rt△OAH中,∵∠OAH=30°,
∴OH=OA=4,
即圆心O到AP的距离为4cm;
(2)连接OF,如图,
∵OH⊥EF,
∴EH=FH,
在Rt△OHF中,HF===3,
∴EF=2HF=6(cm).
15.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
16.(1)证明:过O作OH⊥CD于H,如图1所示:
∵OH⊥CD,
∴CH=DH,AH=BH,
∴AH﹣CH=BH﹣DH,
∴AC=BD;
(2)解:过O作OH⊥CD于H,连接OD,如图2所示:
则CH=DH=CD,
∵OC=OD,∠OCD=60°,
∴△OCD是等边三角形,
∴CD=OC=4,
∴CH=2,
∴OH===2,
∴AH===2,
∴AC=AH﹣CH=2﹣2.
17.解:连接OB,设AB与MN交于点D,如图所示:
∵AC=2,BC=4,
∴AB=AC+BC=6,
∵AB⊥MN,
∴AD=BD=AB=3,∠ODC=∠ODB=90°,
∴CD=AD﹣AC=1,
∴OD===,
∴OB===2,
即⊙O的半径为2.
18.解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA,如图所示:
∴AC=AB=×10=5,
设⊙O的半径为r寸,
在Rt△ACO中,OC=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸.
19.解:过O点作半径OD⊥AB于E,
∴,
在Rt△AEO中,,
∴ED=OD﹣OE=5﹣3=2.
答:水车工作时,盛水桶在水面以下的最大深度为2m.
20.解:如图,连接ON,OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=7.2m,
∴BD=AB=3.6m.
又∵CD=2.4m,
设OB=OC=ON=rm,则OD=(r﹣2.4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,
解得r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面AB2m,
∴CE=2.4﹣2=0.4m,
∴OE=r﹣CE=3.9﹣0.4=3.5m,
在Rt△OEN中,EN2=ON2﹣OE2=3.92﹣3.52=2.96(m2),
∴EN=2.96(m).
∴MN=2EN=2×≈3.44m>3m.
∴此货船能顺利通过这座拱桥
一、选择题
1.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米
B.(4﹣)米
C.2米
D.(4+)米
2.如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )
A.9.6
B.4
C.5
D.10
3.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A.1.0厘米/分
B.0.8厘米/分
C.1.2厘米/分
D.1.4厘米/分
4.往水平放置的半径为13cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=24cm,则水的最大深度为( )
A.5cm
B.8cm
C.10cm
D.12cm
5.如图,拱桥可以近似地看作直径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为150m,那么这些钢索中最长的一根的长度为( )
A.50m
B.40m
C.30m
D.25m
6.已知⊙O的直径CD=100cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=96cm,则AC的长为( )
A.36cm或64cm
B.60cm或80cm
C.80cm
D.60cm
7.如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为( )
A.
B.
C.
D.
8.往直径为26cm的圆柱形容器内装入一些水以后,截面如图所示.若水面宽AB=24cm,则水的最大深度为( )
A.4cm
B.5cm
C.8cm
D.10cm
二、填空题
9.一条排水管的截面如图所示,已知排水管的半径OA=2m,水面宽AB=2.4m,某天下雨后,水管水面上升了0.4m,则此时排水管水面宽CD等于
m.
10.如图,在⊙O中,AC为⊙O直径,B为圆上一点,若∠OBC=26°,则∠AOB的度数为
.
11.如图,矩形ABCD中,AB=6,以点D为圆心,CD长为半径的圆弧与以BC为直径的半圆O相交于点E,若的度数为60°,则直径BC长为
.
12.如图,在平面直角坐标系中,半径为3的⊙O与y轴的负半轴交于点A,点B是⊙O上移动点,点C为弦AB的中点,直线与x轴、y轴分别相交于点D、E,则△CDE面积的最小值为
.
三、解答题
13.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,BC=3.
(1)求AB的长;
(2)求⊙O的半径.
14.已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点.
(1)求圆心O到AP的距离;
(2)求弦EF的长.
15.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
16.如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:AC=BD;
(2)连接OA、OC,若OA=6,OC=4,∠OCD=60°,求AC的长.
17.如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
18.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),求该圆材的直径.
19.如图1,点P表示我国古代水车的一个盛水筒.如图2,当水车工作时,盛水筒的运行路径是以轴心O为圆心,5m为半径的圆.若⊙O被水面截得的弦AB长为8m,求水车工作时,盛水筒在水面以下的最大深度.
20.某地有一座圆弧形拱桥,所在圆的圆心为点O,桥下水面宽度AB为7.2m,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4m(如图).现有一艘宽3m、船舱顶部高出水面AB2m的货船要经过这座拱桥,此货船能否顺利通过这座拱桥?
参考答案
1.解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
2.解:∵OE⊥AC于点E.
∴AE=EC.
∵OE=3,OB=5.
∴AE=.
∴AC=8.
∵∠A=∠A,∠AEO=∠AFC.
∴.
∵CD⊥AB.
∴CD=2CF==9.6.
故选:A.
3.解:设“图上”圆的圆心为O,连接OA,过点O作OD⊥AB于D,如图所示:
∵AB=16厘米,
∴AD=AB=8(厘米),
∵OA=10厘米,
∴OD===6(厘米),
∴海平线以下部分的高度=OA+OD=10+6=16(厘米),
∵太阳从所处位置到完全跳出海平面的时间为16分钟,
∴“图上”太阳升起的速度=16÷16=1.0(厘米/分),
故选:A.
4.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:B.
5.解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=×250=125(m),AC=BC=AB=×150=75(m),
∴OC===100(m),
∴CD=OD﹣OC=125﹣100=25(m),
即这些钢索中最长的一根为25m,
故选:D.
6.解:连接AC,AO,
∵⊙O的直径CD=100cm,AB⊥CD,AB=96cm,
∴AM=AB=×96=48(cm),OD=OC=50(cm),
如图1,∵OA=50cm,AM=48cm,CD⊥AB,
∴OM===14(cm),
∴CM=OC+OM=50+14=64(cm),
∴AC===80(cm);
如图2,同理可得,OM=14cm,
∵OC=50cm,
∴MC=50﹣14=36(cm),
在Rt△AMC中,AC==60(cm);
综上所述,AC的长为80cm或60cm,
故选:B.
7.解:由题意得:⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧于点H、I,连接OF,如图所示:
∵四边形ABCD是矩形,
∴AD∥BC,
∵IG⊥BC,
∴IG⊥AD,
∴FH=EF=1,
设⊙O的半径为r,则OH=2﹣r,
在Rt△OFH中,由勾股定理得:r2﹣(2﹣r)2=12,
解得:r=,
即球的半径长为,
故选:C.
8.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵⊙O的直径为26cm,
∴OB=OC=13(cm),
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:C.
9.解:过O作OE⊥AB于E,交CD于F,连接OC,如图所示:
则AE=BE=AB=1.2(m),OF⊥CD,
∴CF=DF=CD,
∴OE===1.6(m),
∵水管水面上升了0.4m,
∴OF=OE﹣EF=1.6﹣0.4=1.2(m),
∴CF===1.6(m),
∴CD=2CF=3.2(m)
故答案为:3.2.
10.解:∵∠OBC=26°,OB=OC,
∴∠C=∠OBC=26°,
∴∠AOB=2∠C=52°,
故答案为:52°.
11.解:如图,连接BE,EC.
∵BC是直径,
∴∠BEC=90°,
∵的度数=60°,
∴∠BCE=×60°=30°,
∵四边形ABCD是矩形,
∴AB=CD=6,∠DCB=90°,
∴∠DCE=90°﹣30°=60°,
∵DE=DC,
∴△DEC是等边三角形,
∴EC=CD=6,
∴BC=4.
故答案为:.
12.解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.
∵AC=CB,AM=OM,
∴MC=OB=,
∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.
∵直线y=﹣x﹣5与x轴、y轴分别交于点D、E,
∴D(﹣12,0),E(0,﹣5),
∴OD=12,OE=5,
∴DE===13,
∵∠MDN=∠ODE,∠MND=∠DOE,
∴MN=,
当点C与C′重合时,△C′DE的面积最小,△C′DE的面积最小值=×13×(﹣)=,
故答案为:.
13.解:(1)连接AC,如图,
∵CD⊥AB,
∴AF=BF,即CD垂直平分AB,
∴CA=CB=3,
∵AO⊥BC,
∴CE=BE,即AE垂直平分BC,
∴AB=AC=3;
(2)∵AB=AC=BC,
∴△ABC为等边三角形,
∴∠BAC=60°,
∴AE⊥BC,
∴AE平分∠BAC,即∠OAF=30°,
在Rt△OAF中,∵OF=AF=×=,
∴OA=2OF=,
即⊙O的半径为.
14.解:(1)过O点作OH⊥EF于H,如图,
∵DB=10,
∴OD=5,
∴OA=AD+OD=3+5=8,
在Rt△OAH中,∵∠OAH=30°,
∴OH=OA=4,
即圆心O到AP的距离为4cm;
(2)连接OF,如图,
∵OH⊥EF,
∴EH=FH,
在Rt△OHF中,HF===3,
∴EF=2HF=6(cm).
15.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
16.(1)证明:过O作OH⊥CD于H,如图1所示:
∵OH⊥CD,
∴CH=DH,AH=BH,
∴AH﹣CH=BH﹣DH,
∴AC=BD;
(2)解:过O作OH⊥CD于H,连接OD,如图2所示:
则CH=DH=CD,
∵OC=OD,∠OCD=60°,
∴△OCD是等边三角形,
∴CD=OC=4,
∴CH=2,
∴OH===2,
∴AH===2,
∴AC=AH﹣CH=2﹣2.
17.解:连接OB,设AB与MN交于点D,如图所示:
∵AC=2,BC=4,
∴AB=AC+BC=6,
∵AB⊥MN,
∴AD=BD=AB=3,∠ODC=∠ODB=90°,
∴CD=AD﹣AC=1,
∴OD===,
∴OB===2,
即⊙O的半径为2.
18.解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA,如图所示:
∴AC=AB=×10=5,
设⊙O的半径为r寸,
在Rt△ACO中,OC=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸.
19.解:过O点作半径OD⊥AB于E,
∴,
在Rt△AEO中,,
∴ED=OD﹣OE=5﹣3=2.
答:水车工作时,盛水桶在水面以下的最大深度为2m.
20.解:如图,连接ON,OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=7.2m,
∴BD=AB=3.6m.
又∵CD=2.4m,
设OB=OC=ON=rm,则OD=(r﹣2.4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,
解得r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面AB2m,
∴CE=2.4﹣2=0.4m,
∴OE=r﹣CE=3.9﹣0.4=3.5m,
在Rt△OEN中,EN2=ON2﹣OE2=3.92﹣3.52=2.96(m2),
∴EN=2.96(m).
∴MN=2EN=2×≈3.44m>3m.
∴此货船能顺利通过这座拱桥
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
