3.4简单机械 杠杆学案（无答案）

杠杆学案
1．杠杆
(1)定义：在力的作用下，能绕固定点转动的硬棒叫杠杆.
(2)杠杆五要素：支点、动力、阻力、动力臂、阻力臂
支点：杠杜绕着转动的固定点叫做杠杆的支点。
（找支点是第一步，也是关键，告诉学生可让杠杆转一下）
动力：使杠杆转动的力。
在实际确定动力时,要看我们使用杠杆工作时为了达到预期目的,需要杠杆向哪个方向转动,能使杠杆向需要方向转动的力,不论是哪个物体施加的力,就是作用在杠杆上的动力。
阻力：阻碍杠杆转动的力。
和确定动力时的方法相同,由力的转动效果来决定,阻碍杠杆向需要方向转动的力就是阻力。
动力臂：从支点到动力作用线的距离叫做动力臂。
动力作用线就是通过动力作用点,沿动力的方向所画的直线。动力臂就是从支点到动力作用线所画的垂线长,也就是几何学中的点到线的距离。
阻力臂：从支点到阻力作用线的距离叫做阻力臂。
(3)杠杆平衡条件：
杠杆的平衡条件是：动力×动力臂＝阻力×阻力臂
写成公式就是:F1·l1＝F2·l2或写成比例式:＝
(4)杠杆的应用及分类
杠杆的实际应用中,可分为三类
省力杠杆：其动力臂l1?大于阻力臂l2,平衡时动力F1小于阻力F2,即用较小的动力就可以克服较大的阻力.但是实际工作时动力移动的距离却比阻力移动的距离大,即要费距离.如撬起重物的撬棒,开启瓶盖的起子、铡草用的铡刀等,都属于这一类杠杆.
费力杠杆：这类杠杆的特点是动力臂l1小于阻力臂l2,平衡时动力F1大于阻力F2,即要用较大的动力才能克服阻力完成工作,但它的优点是杠杆工作时,动力移动较小的距离就能使阻力移动较大的距离.使工作方便,也就是省了距离.如缝纫机踏板、挖土的铁锨、大扫帚、夹煤块的火钳,这些杠杆都是费力杠杆.
等臂杠杆：这类杠杆的动力臂l1等于阻力臂l2,平衡时动力F1等于阻力F2,工作时既不省力也不费力,如天平、定滑轮就是等臂杠杆。
杆杆解题思路
只要是杠杆问题，不外乎寻找：支点、力、力臂、平衡方程这四个条件中的一个或几个。按下面四步进行解答，所有问题都可迎刃而解：
1.支点：
找支点的方法是——支点一定是固定不动的，并且整个杠杆绕着它转动。两个条件缺一不可。
2.力：
找“力”的方法是两步走——第一步，确定是否要考虑杠杆本身重力（这一步很关键，题目往往在这里设陷阱！），一般重力的作用点（重心）选在物体的对称中心；第二步，确定与杠杆接触的物体施加在杠杆上的力。注意：不要有遗漏。
3.力臂：
找力臂的方法是——从支点出发，向力的作用线（经常要延长成直线）作垂线段，垂线段的长度就是力臂的长度。
4.平衡方程：
列平衡方程的方法是——（1）如果动力、阻力各一个：动力×动力臂＝阻力×阻力臂。
（2）如果动力、阻力不止一个：动力1×动力臂1+动力2×动力臂2+……＝阻力1×阻力臂1+阻力2×阻力臂2+……。
剩下的工作，当然就是把这个方程解出来！
中考杠杆试题归类点拨
题型一：会确认并画出杠杆的力臂
例1
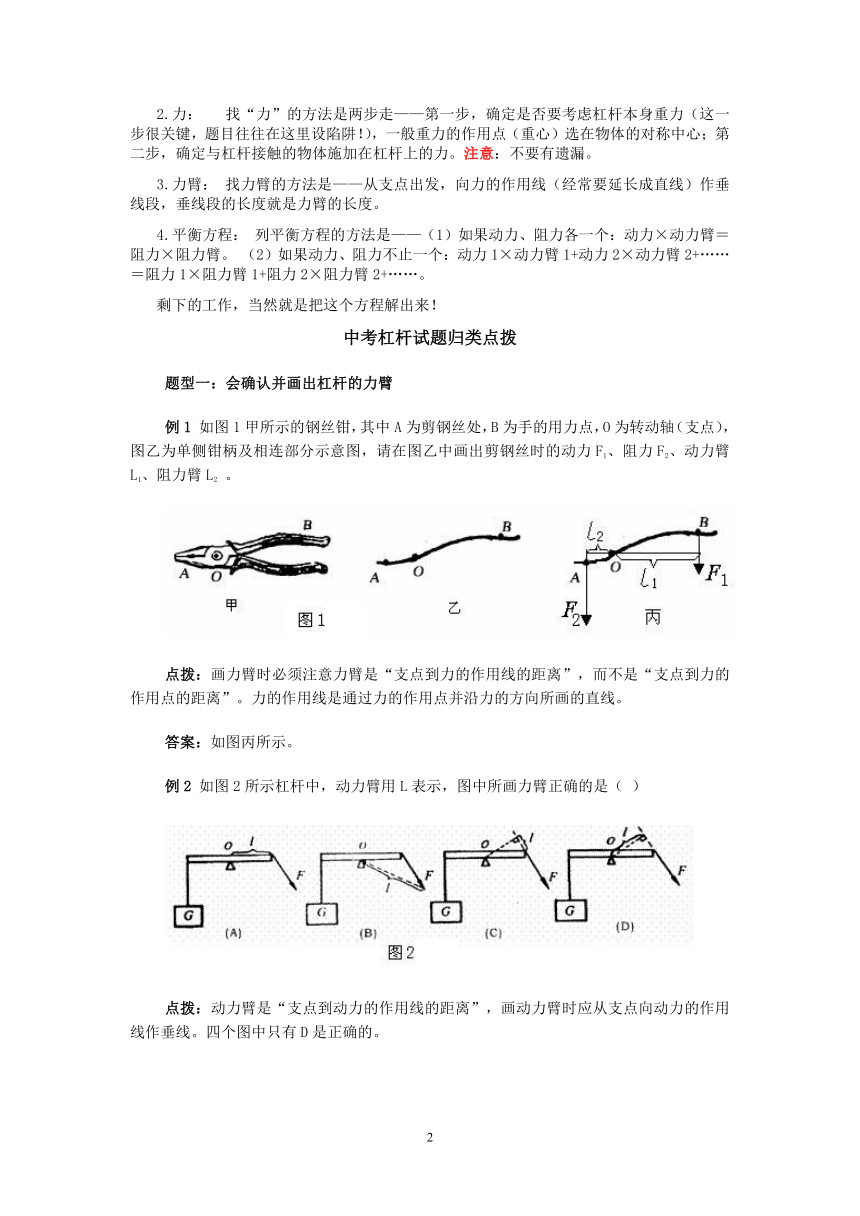
如图1甲所示的钢丝钳，其中A为剪钢丝处，B为手的用力点，O为转动轴（支点），图乙为单侧钳柄及相连部分示意图，请在图乙中画出剪钢丝时的动力F1、阻力F2、动力臂L1、阻力臂L2
。
点拨：画力臂时必须注意力臂是“支点到力的作用线的距离”，而不是“支点到力的作用点的距离”。力的作用线是通过力的作用点并沿力的方向所画的直线。
答案：如图丙所示。
例2
如图2所示杠杆中，动力臂用L表示，图中所画力臂正确的是（
）
点拨：动力臂是“支点到动力的作用线的距离”，画动力臂时应从支点向动力的作用线作垂线。四个图中只有D是正确的。
题型二：判断是省力杠杆还是费力杠杆
例3
下列工具中，属于省力杠杆的是(　)
A．夹邮票用的镊子
B．理发师修剪头发用的剪刀
C．剪铁丝用的钢丝钳
D．钓鱼用的鱼竿
点拨：根据杠杆平衡条件，我们把杠杆分为三类：省力杠杆、费力杠杆和等臂杠杆。如果动力臂比阻力臂长，就是省力杠杆；如果动力臂比阻力臂短，就是费力杠杆；如果动力臂和阻力臂相等，就是等臂杠杆。上面例子的实质都是考查的杠杆的分类。A、B、D三种杠杆均是阻力臂大于动力臂，所以它们都是费力杠杆。
例4
人体的运动系统相当复杂，但最基本的运动形式是，骨骼在肌肉提供的动力作用下绕关节转动。如图3所示是手端起茶杯的情景，其前臂骨骼相当于杠杆，肱二头肌收缩提供动力。由图3可以看出，这是一个（　）
A．费力、省距离的杠杆
B．省力、费距离的杠杆
C．既费力，也费距离的杠杆
D．既省力，也省距离的杠杆
点拨：本题与生活实际相联系，由于人的前臂相当于杠杆，动力臂和阻力臂已经固定，且阻力臂大于动力臂，是一个费力杠杆。根据杠杆平衡条件可知：在动力臂和阻力臂确定的情况下，手托起的物体越重，肌肉提供的动力越大，感觉越累。
答案：A
例5
杠杆在我国古代就有了许多巧妙的应用。护城河上安装使用的吊桥就是一个杠杆，由图4可知它的支点是______点(填“A”、B”或“C”)，在匀速拉起时，它属于一个______杠杆(填“省力”或“费力”)，并在图中画动力臂L1。
点拨：杠杆的动力和阻力指的都是杠杆吊桥受到的力，所以动力是绳对吊桥的作用力，阻力是吊桥的自身的重力。确定吊桥这个杠杆动力臂和阻力臂的关系，需要找到支点，如图支点在C点，动力臂L1大于阻力臂CO，吊桥是一个省力杠杆。动力臂L1如图5所示。
题型三：有关杠杆平衡条件的实验题及应用题
例6
在探究杠杆的平衡条件实验中：
1．小军将杠杆放在水平桌面上，发现杠杆左端下倾。那么他应将杠杆右端螺母向______
(填“左”或“右”)调节一些，使杠杆在______位置平衡。
2．实验时只有8个相同的钩码，杠杆上画有均匀的格子，当在A点挂4个钩码如图6所示，则怎样挂钩码可以使杠杆在水平位置平衡？(请设计两种方案)
答：①____________________________
②__________________________。
点拨：解题的关键是依据杠杆的平衡条件，看左、右两边的力和力臂的乘积是否相等。若乘积相等，则杠杆平衡；若乘积不等，那么杠杆将向乘积大的一边下倾。
答案：1．（1）右；（2）水平。
2．①2个钩码挂在“6”处；②3个钩码挂在“4”处等。
例8
一根长1m左右、粗细均匀的细木棒，一个已知质量为m的钩码，一把刻度尺，还有一些细绳和一只铅笔。只用这些器材如何测出这根细棒的质量？写出实验步骤及导出计算木棒质量的公式。
点拨：细木棒可看作杠杆，利用杠杆平衡条件来求解，关键是找到一个合适的支点，使挂有钩码的细木棒在水平位置平衡。用刻度尺测出力臂，即可求出木棒的质量。
实验步骤：
(1)用刻度尺找出木棒重心，用铅笔在重心处做出标记C；如图7所示；
(2)用细线系住木棒上的某一点作为杠杆上的支点；
（3）把质量为m的钩码用细线系好后套在木棒上；
（4）左、右调节钩码或支点的位置使木棒在水平位置平衡；
（5）用刻度尺分别量出支点到木棒重心及支点到系钩码细线的距离L1和L2。
计算：设木棒质量为M，根据杠杆的平衡条件可得出MgL1=mgL2
即ML1=mL2
所以木棒的质量为
1