2.5.1 离散型随机变量的均值 课件(苏教版选修2-3)
文档属性
| 名称 | 2.5.1 离散型随机变量的均值 课件(苏教版选修2-3) |  | |
| 格式 | zip | ||
| 文件大小 | 993.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-11 09:15:07 | ||
图片预览









文档简介
(共41张PPT)
2.5.1 离散型随机变量的均值 课件(苏教版选修2-3)
课堂互动讲练
知能优化训练
课前自主学案
学习目标
2.5.1
1.掌握离散型随机变量的均值的概念及计算方法.
2.掌握超几何分布、二项分布的均值.
3.会用均值分析解决简单的实际问题.
学习目标
课前自主学案
温故夯基
2.两点分布的分布列是
3.若X~B(n,p),则P(X=k)=____________________,k=0,1,2,…,n,其p称成功概率.
X 0 1
P 1-p p
知新益能
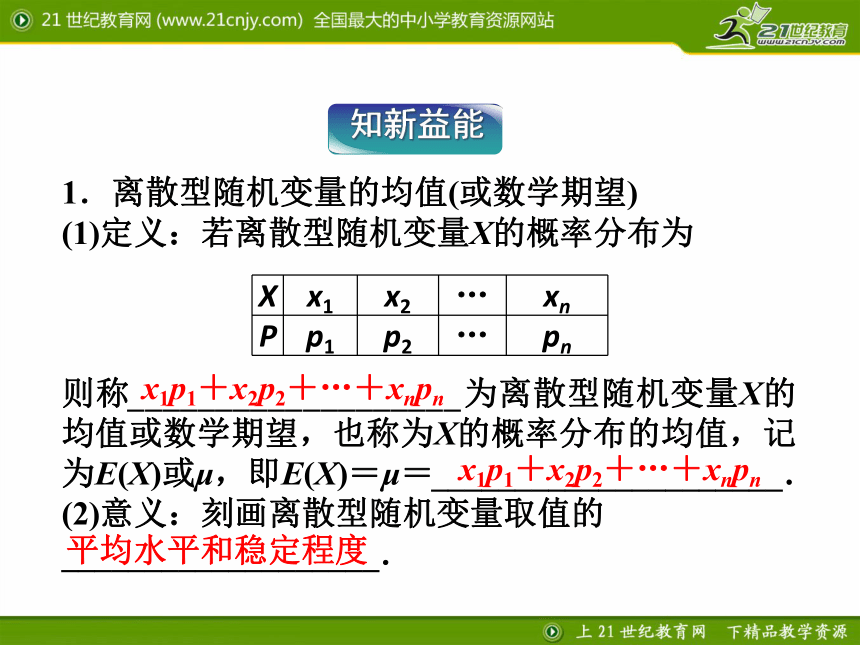
1.离散型随机变量的均值(或数学期望)
(1)定义:若离散型随机变量X的概率分布为
则称___________________为离散型随机变量X的均值或数学期望,也称为X的概率分布的均值,记为E(X)或μ,即E(X)=μ=_____________________.
(2)意义:刻画离散型随机变量取值的___________________.
X x1 x2 … xn
P p1 p2 … pn
x1p1+x2p2+…+xnpn
x1p1+x2p2+…+xnpn
平均水平和稳定程度
np
问题探究
1.在实际问题中,为什么能用样本均值来估计总体均值?
提示:随机变量总体的均值是一个常数,不受其他因素的影响,而样本均值是一个随机变量,它随着样本的不同而变化,当样本容量趋于无穷大时,样本均值就越来越接近于总体的均值.因此,我们常用样本均值来估计总体均值.
2.若随机变量X等可能地取1,2,3,…,n,其均值为多少?
课堂互动讲练
求离散型随机变量的数学期望
考点突破
求数学期望(期值)的关键是求出其分布列,然后套用数学期望(均值)公式求解.
例1
(2011年高考江西卷)某饮料公司招聘了一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料.若4杯都选对,则月工资定为3 500元;若4杯选对3杯,则月工资定为2 800元;否则月工资定为2 100元.令X表示此人选对A饮料的杯数,假设此人对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的期望.
【名师点评】 随机变量的均值是一个常数,它不依赖于样本的抽取,只要找清随机变量及相应的概率即可计算.
变式训练1 在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在一起,若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,…,6),求:
(1)甲、乙两单位的演出序号至少有一个为奇数的概率;
(2)甲、乙两单位之间的演出单位个数ξ的分布列与期望.
超几何分布及二项分布的均值
例2
某校高二年级组织的一次数学测试由30个选择题构成,每个选择题有4个选项,其中仅有一个选项正确.每题选对得5分,不选或选错不得分,满分150分,学生甲乙选对任意一题的概率分别为0.9,0.5,分别求学生甲和学生乙在这次测试中的成绩的期望.
【思路点拨】 由题意,可知甲、乙两名学生选对的题数成二项分布,求得选对题的数学期望,便可计算出成绩的数学期望.
【解】 设学生甲和学生乙在这次测试中选对的题数分别是X1和X2,则X1~B(30,0.9),X2~B(30,0.5),
所以E(X1)=30×0.9=27;E(X2)=30×0.5=15.
由于每题选对得5分,所以学生甲和学生乙在这次测试中的成绩分别是5X1和5X2,这样,他们在测试中的成绩的期望分别是:
E(5X1)=5E(X1)=5×27=135,
E(5X2)=5E(X2)=5×15=75.
【名师点评】 超几何分布和二项分布是两种特殊的而且应用相当广泛的分布列,解题时如果能发现是这两种分布模型,就可以直接有规律地写出分布列,求出期望值.
均值的实际应用
在实际生活中,常利用随机变量均值的大小决定某些方案的优劣,解决一些决策问题.
例3
(本题满分14分)(2011年沂源高二检测)随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为ξ.
(1)求ξ的分布列;
(2)求1件产品的平均利润(即ξ的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
【思路点拨】 解答本题应先根据题意求ξ的分布列,再计算数学期望回答有关问题.
(2)E(ξ)=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34.9分
(3)设技术革新后的三等品率为x,则此时1件产品的平均利润为E(x)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01=4.76-x(0≤x≤0.29).11分
依题意,E(x)≥4.73,即4.76-x≥4.73.
解得x≤0.03,所以三等品率最多为3%.14分
【名师点评】 解答此类题目,应首先把实际问题概率模型化,然后利用有关概率的知识去分析相应各事件可能性的大小,并列出分布列,最后利用有关的公式求出相应的概率及数学期望.
变式训练3 A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员为B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下:
现按表中对阵方式出场,每场胜队得1分,负队得0分.设A队、B队最后总得分分别为ξ、η.求
(1)ξ、η的概率分布;
(2)E(ξ)、E(η).
方法感悟
1.求离散型随机变量均值的步骤:
(1)确定离散型随机变量X的取值;
(2)写出分布列,并检查分布列的正确与否;
(3)根据公式求出均值.
2.若X、Y是两个随机变量,且Y=aX+b,则E(Y)=aE(X)+b,即随机变量X的线性函数的数学期望等于这个随机变量的期望E(X)的同一线性函数.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
2.5.1 离散型随机变量的均值 课件(苏教版选修2-3)
课堂互动讲练
知能优化训练
课前自主学案
学习目标
2.5.1
1.掌握离散型随机变量的均值的概念及计算方法.
2.掌握超几何分布、二项分布的均值.
3.会用均值分析解决简单的实际问题.
学习目标
课前自主学案
温故夯基
2.两点分布的分布列是
3.若X~B(n,p),则P(X=k)=____________________,k=0,1,2,…,n,其p称成功概率.
X 0 1
P 1-p p
知新益能
1.离散型随机变量的均值(或数学期望)
(1)定义:若离散型随机变量X的概率分布为
则称___________________为离散型随机变量X的均值或数学期望,也称为X的概率分布的均值,记为E(X)或μ,即E(X)=μ=_____________________.
(2)意义:刻画离散型随机变量取值的___________________.
X x1 x2 … xn
P p1 p2 … pn
x1p1+x2p2+…+xnpn
x1p1+x2p2+…+xnpn
平均水平和稳定程度
np
问题探究
1.在实际问题中,为什么能用样本均值来估计总体均值?
提示:随机变量总体的均值是一个常数,不受其他因素的影响,而样本均值是一个随机变量,它随着样本的不同而变化,当样本容量趋于无穷大时,样本均值就越来越接近于总体的均值.因此,我们常用样本均值来估计总体均值.
2.若随机变量X等可能地取1,2,3,…,n,其均值为多少?
课堂互动讲练
求离散型随机变量的数学期望
考点突破
求数学期望(期值)的关键是求出其分布列,然后套用数学期望(均值)公式求解.
例1
(2011年高考江西卷)某饮料公司招聘了一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料.若4杯都选对,则月工资定为3 500元;若4杯选对3杯,则月工资定为2 800元;否则月工资定为2 100元.令X表示此人选对A饮料的杯数,假设此人对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的期望.
【名师点评】 随机变量的均值是一个常数,它不依赖于样本的抽取,只要找清随机变量及相应的概率即可计算.
变式训练1 在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在一起,若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,…,6),求:
(1)甲、乙两单位的演出序号至少有一个为奇数的概率;
(2)甲、乙两单位之间的演出单位个数ξ的分布列与期望.
超几何分布及二项分布的均值
例2
某校高二年级组织的一次数学测试由30个选择题构成,每个选择题有4个选项,其中仅有一个选项正确.每题选对得5分,不选或选错不得分,满分150分,学生甲乙选对任意一题的概率分别为0.9,0.5,分别求学生甲和学生乙在这次测试中的成绩的期望.
【思路点拨】 由题意,可知甲、乙两名学生选对的题数成二项分布,求得选对题的数学期望,便可计算出成绩的数学期望.
【解】 设学生甲和学生乙在这次测试中选对的题数分别是X1和X2,则X1~B(30,0.9),X2~B(30,0.5),
所以E(X1)=30×0.9=27;E(X2)=30×0.5=15.
由于每题选对得5分,所以学生甲和学生乙在这次测试中的成绩分别是5X1和5X2,这样,他们在测试中的成绩的期望分别是:
E(5X1)=5E(X1)=5×27=135,
E(5X2)=5E(X2)=5×15=75.
【名师点评】 超几何分布和二项分布是两种特殊的而且应用相当广泛的分布列,解题时如果能发现是这两种分布模型,就可以直接有规律地写出分布列,求出期望值.
均值的实际应用
在实际生活中,常利用随机变量均值的大小决定某些方案的优劣,解决一些决策问题.
例3
(本题满分14分)(2011年沂源高二检测)随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为ξ.
(1)求ξ的分布列;
(2)求1件产品的平均利润(即ξ的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
【思路点拨】 解答本题应先根据题意求ξ的分布列,再计算数学期望回答有关问题.
(2)E(ξ)=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34.9分
(3)设技术革新后的三等品率为x,则此时1件产品的平均利润为E(x)=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01=4.76-x(0≤x≤0.29).11分
依题意,E(x)≥4.73,即4.76-x≥4.73.
解得x≤0.03,所以三等品率最多为3%.14分
【名师点评】 解答此类题目,应首先把实际问题概率模型化,然后利用有关概率的知识去分析相应各事件可能性的大小,并列出分布列,最后利用有关的公式求出相应的概率及数学期望.
变式训练3 A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员为B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下:
现按表中对阵方式出场,每场胜队得1分,负队得0分.设A队、B队最后总得分分别为ξ、η.求
(1)ξ、η的概率分布;
(2)E(ξ)、E(η).
方法感悟
1.求离散型随机变量均值的步骤:
(1)确定离散型随机变量X的取值;
(2)写出分布列,并检查分布列的正确与否;
(3)根据公式求出均值.
2.若X、Y是两个随机变量,且Y=aX+b,则E(Y)=aE(X)+b,即随机变量X的线性函数的数学期望等于这个随机变量的期望E(X)的同一线性函数.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
