2.5.2 离散型随机变量的方差与标准差 课件(苏教版选修2-3)
文档属性
| 名称 | 2.5.2 离散型随机变量的方差与标准差 课件(苏教版选修2-3) |  | |
| 格式 | zip | ||
| 文件大小 | 646.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-11 09:15:26 | ||
图片预览










文档简介
(共31张PPT)
2.5.2 离散型随机变量的方差与标准差 课件(苏教版选修2-3)
课堂互动讲练
知能优化训练
课前自主学案
学习目标
2.5.2
1.理解离散型随机变量的方差的概念、意义及计算方法.
2.能用方差(标准差)来分析解决实际问题.
学习目标
课前自主学案
温故夯基
1.若离散型随机变量X的分布列为
X x1 x2 … xi … xn
P p1 p2 … pi … pn
E(X)=_______________________________,它反映了离散型随机变量取值的_______水平.
2.若X~B(n,p),则E(X)=______.
x1p1+x2p2+…+xipi+…+xnpn
平均
np
知新益能
1.离散型随机变量的方差和标准差
(1)离散型随机变量的方差
①定义:设离散型随机变量X的均值为μ,其概率分布为
X x1 x2 … xn
P p1 p2 … pn
(x1-μ)2p1+(x2-μ)2p2+…+(xn-μ)2pn
σ2
平均偏离
算术平方根
p(1-p)
np(1-p)
问题探究
1.随机变量的方差和样本的方差都是变量吗?
提示:样本的方差是随着样本的不同而变化的,因此它是一个随机变量,而随机变量的方差是通过大量试验得出的,刻画了随机变量X与其均值E(X)的平均偏离程度,因此它是一个常数(量)而非变量.
2.方差、标准差的单位与随机变量的单位有什么关系?
提示:方差的单位是随机变量单位的平方;标准差与随机变量本身有相同的单位.
课堂互动讲练
求离散型随机变量的方差
考点突破
根据离散型随机变量的分布列、期望、方差公式求解.
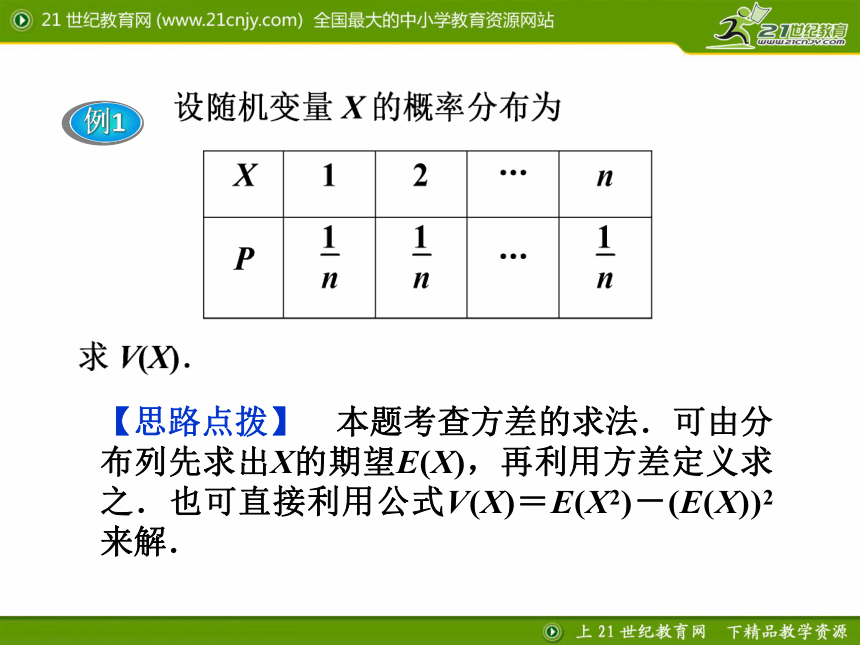
例1
【思路点拨】 本题考查方差的求法.可由分布列先求出X的期望E(X),再利用方差定义求之.也可直接利用公式V(X)=E(X2)-(E(X))2来解.
变式训练1 已知随机变量X的概率分布表为:
求V(X).
解:法一:E(X)=0.1×0+0.15×1+0.25×2+0.25×3+0.15×4+0.1×5=2.5,
V(X)=(0-2.5)2×0.1+(1-2.5)2×0.15+(2-2.5)2×0.25+(3-2.5)2×0.25+(4-2.5)2×0.15+(5-2.5)2×0.1
=0.625+0.3375+0.0625+0.0625+0.3375+0.625=2.05.
X 0 1 2 3 4 5
P 0.1 0.15 0.25 0.25 0.15 0.1
两点分布与二项分布的方差、标准差
确定是两点分布或二项分布后,直接用公式求解即可.
例2
一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分.学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个.求学生甲和乙在这次英语单元测验中的成绩的期望和方差.
【思路点拨】 设学生甲和乙在这次英语测验中正确解答的选择题个数分别是ξ,η,则ξ~B(20,0.9),η~B(20,0.25).利用二项分布的期望公式E(X)=np,方差公式V(X)=npq直接计算.
【解】 设学生甲和乙在这次英语测验中正确答案的选择个数分别是ξ,η,则ξ ~B(20,0.9),η ~B(20.0,25),
∴E(ξ)=20×0.9=18,E(η)=20×0.25=5.
V(ξ)=np甲q甲=20×0.9×0.1=1.8,
V(η)=np乙q乙=20×0.25×0.75=5×0.75=3.75.
由于答对每题得5分,学生甲和乙在这次英语测验中的成绩分别是5ξ和5η.所以,他们在测验中的成绩的期望和方差分别是
E(5ξ)=5E(ξ)=5×18=90,
E(5η)=5E(η)=5×5=25.
V(5ξ)=25 V(ξ)=25×1.8=45,
V(5η)=25V(η)=25×3.75=93.75.
【名师点评】 随机变量的期望与方差具有下列运算性质:
E(aX+b) V(aX+b)
a=0 b 0
a=1 E(X)+b V(X)
a≠1 aE(X)+b a2V(X)
变式训练2 某人投弹命中目标的概率为p=0.8.
(1)求投弹一次,命中次数X的均值和方差;
(2)求重复10次投弹时命中次数Y的均值和方差.
解:(1)X的分布列为:
E(X)=0×0.2+1×0.8=0.8.
V(X)=(0-0.8)2×0.2+(1-0.8)2×0.8=0.16.
(2)由题意知,命中次数Y服从二项分布,即Y~B(10,0.8),
∴E(Y)=np=10×0.8=8,
V(Y)=10×0.8×0.2=1.6.
X 0 1
P 0.2 0.8
期望、方差、分布列的综合应用
数学期望反映随机变量取值的平均水平,方差则反映随机变量取值的稳定与波动、集中与离散的程度.
例3
(本题满分14分)在一个不透明的纸袋里装有5个大小相同的小球,其中有1个红球和4个黄球,规定每次从袋中任意摸出一球,若摸出的是黄球则不再放回,直到摸出红球为止,求摸球次数ξ的期望和方差.
ξ 1 2 3 4 5
P 0.2 0.2 0.2 0.2 0.2
8分
由定义知:E(ξ)=0.2×(1+2+3+4+5)=3,
V(ξ)=0.2×(22+12+02+12+22)=2.14分
【名师点评】 求离散型随机变量X的均值与方差的基本步骤:
(1)理解X的意义,写出X可能取的全部值;
(2)求X取每个值的概率;
(3)写出X的分布列;
(4)由均值的定义求E(X);
(5)由方差的定义求V(X).
变式训练3 有甲、乙两个建材厂,都想投标参加某重点建设,为了对重点建设负责,政府到两建材厂抽样检查,他们从中各取等量的样品检查它们的抗拉强度指数如下:
X 110 120 125 130 135
P 0.1 0.2 0.4 0.1 0.2
Y 100 115 125 130 145
P 0.1 0.2 0.4 0.1 0.2
其中X和Y分别表示甲、乙两厂材料的抗拉强度,试比较甲、乙两厂材料哪一种稳定性较好?
解:E(X)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(Y)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
V(X)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(135-125)2=50,
V(Y)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165.
由于E(X)=E(Y),而V(X)方法感悟
1.求随机变量ξ的均值、方差的一般步骤
(1)写出ξ的分布列.在求ξ取每一个值的概率时,要联系概率的有关知识如分布列,在求ξ取每一个值的概率时,要联系概率的有关知识如古典概型、互斥事件的概率、独立事件的概率等.
(2)由分布列求E(ξ),进而求出V(ξ).
(3)如果随机变量是线性关系或服从两点分布、二项分布,根据它们的期望、方差公式计算.
2.期望(均值)仅体现了随机变量取值的平均水平
当我们希望实际的平均水平比较理想时,则先求它们的均值,但不要误认为均值相等时,它们都一样好,这时,还应看它们相对于均值的偏离程度,也就是看哪一个相对稳定(即计算方差的大小),稳定者就更好.如果我们希望比较稳定时,这时应先考虑方差,再考虑均值是否接近即可.
2.5.2 离散型随机变量的方差与标准差 课件(苏教版选修2-3)
课堂互动讲练
知能优化训练
课前自主学案
学习目标
2.5.2
1.理解离散型随机变量的方差的概念、意义及计算方法.
2.能用方差(标准差)来分析解决实际问题.
学习目标
课前自主学案
温故夯基
1.若离散型随机变量X的分布列为
X x1 x2 … xi … xn
P p1 p2 … pi … pn
E(X)=_______________________________,它反映了离散型随机变量取值的_______水平.
2.若X~B(n,p),则E(X)=______.
x1p1+x2p2+…+xipi+…+xnpn
平均
np
知新益能
1.离散型随机变量的方差和标准差
(1)离散型随机变量的方差
①定义:设离散型随机变量X的均值为μ,其概率分布为
X x1 x2 … xn
P p1 p2 … pn
(x1-μ)2p1+(x2-μ)2p2+…+(xn-μ)2pn
σ2
平均偏离
算术平方根
p(1-p)
np(1-p)
问题探究
1.随机变量的方差和样本的方差都是变量吗?
提示:样本的方差是随着样本的不同而变化的,因此它是一个随机变量,而随机变量的方差是通过大量试验得出的,刻画了随机变量X与其均值E(X)的平均偏离程度,因此它是一个常数(量)而非变量.
2.方差、标准差的单位与随机变量的单位有什么关系?
提示:方差的单位是随机变量单位的平方;标准差与随机变量本身有相同的单位.
课堂互动讲练
求离散型随机变量的方差
考点突破
根据离散型随机变量的分布列、期望、方差公式求解.
例1
【思路点拨】 本题考查方差的求法.可由分布列先求出X的期望E(X),再利用方差定义求之.也可直接利用公式V(X)=E(X2)-(E(X))2来解.
变式训练1 已知随机变量X的概率分布表为:
求V(X).
解:法一:E(X)=0.1×0+0.15×1+0.25×2+0.25×3+0.15×4+0.1×5=2.5,
V(X)=(0-2.5)2×0.1+(1-2.5)2×0.15+(2-2.5)2×0.25+(3-2.5)2×0.25+(4-2.5)2×0.15+(5-2.5)2×0.1
=0.625+0.3375+0.0625+0.0625+0.3375+0.625=2.05.
X 0 1 2 3 4 5
P 0.1 0.15 0.25 0.25 0.15 0.1
两点分布与二项分布的方差、标准差
确定是两点分布或二项分布后,直接用公式求解即可.
例2
一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分.学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个.求学生甲和乙在这次英语单元测验中的成绩的期望和方差.
【思路点拨】 设学生甲和乙在这次英语测验中正确解答的选择题个数分别是ξ,η,则ξ~B(20,0.9),η~B(20,0.25).利用二项分布的期望公式E(X)=np,方差公式V(X)=npq直接计算.
【解】 设学生甲和乙在这次英语测验中正确答案的选择个数分别是ξ,η,则ξ ~B(20,0.9),η ~B(20.0,25),
∴E(ξ)=20×0.9=18,E(η)=20×0.25=5.
V(ξ)=np甲q甲=20×0.9×0.1=1.8,
V(η)=np乙q乙=20×0.25×0.75=5×0.75=3.75.
由于答对每题得5分,学生甲和乙在这次英语测验中的成绩分别是5ξ和5η.所以,他们在测验中的成绩的期望和方差分别是
E(5ξ)=5E(ξ)=5×18=90,
E(5η)=5E(η)=5×5=25.
V(5ξ)=25 V(ξ)=25×1.8=45,
V(5η)=25V(η)=25×3.75=93.75.
【名师点评】 随机变量的期望与方差具有下列运算性质:
E(aX+b) V(aX+b)
a=0 b 0
a=1 E(X)+b V(X)
a≠1 aE(X)+b a2V(X)
变式训练2 某人投弹命中目标的概率为p=0.8.
(1)求投弹一次,命中次数X的均值和方差;
(2)求重复10次投弹时命中次数Y的均值和方差.
解:(1)X的分布列为:
E(X)=0×0.2+1×0.8=0.8.
V(X)=(0-0.8)2×0.2+(1-0.8)2×0.8=0.16.
(2)由题意知,命中次数Y服从二项分布,即Y~B(10,0.8),
∴E(Y)=np=10×0.8=8,
V(Y)=10×0.8×0.2=1.6.
X 0 1
P 0.2 0.8
期望、方差、分布列的综合应用
数学期望反映随机变量取值的平均水平,方差则反映随机变量取值的稳定与波动、集中与离散的程度.
例3
(本题满分14分)在一个不透明的纸袋里装有5个大小相同的小球,其中有1个红球和4个黄球,规定每次从袋中任意摸出一球,若摸出的是黄球则不再放回,直到摸出红球为止,求摸球次数ξ的期望和方差.
ξ 1 2 3 4 5
P 0.2 0.2 0.2 0.2 0.2
8分
由定义知:E(ξ)=0.2×(1+2+3+4+5)=3,
V(ξ)=0.2×(22+12+02+12+22)=2.14分
【名师点评】 求离散型随机变量X的均值与方差的基本步骤:
(1)理解X的意义,写出X可能取的全部值;
(2)求X取每个值的概率;
(3)写出X的分布列;
(4)由均值的定义求E(X);
(5)由方差的定义求V(X).
变式训练3 有甲、乙两个建材厂,都想投标参加某重点建设,为了对重点建设负责,政府到两建材厂抽样检查,他们从中各取等量的样品检查它们的抗拉强度指数如下:
X 110 120 125 130 135
P 0.1 0.2 0.4 0.1 0.2
Y 100 115 125 130 145
P 0.1 0.2 0.4 0.1 0.2
其中X和Y分别表示甲、乙两厂材料的抗拉强度,试比较甲、乙两厂材料哪一种稳定性较好?
解:E(X)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(Y)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
V(X)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(135-125)2=50,
V(Y)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165.
由于E(X)=E(Y),而V(X)
1.求随机变量ξ的均值、方差的一般步骤
(1)写出ξ的分布列.在求ξ取每一个值的概率时,要联系概率的有关知识如分布列,在求ξ取每一个值的概率时,要联系概率的有关知识如古典概型、互斥事件的概率、独立事件的概率等.
(2)由分布列求E(ξ),进而求出V(ξ).
(3)如果随机变量是线性关系或服从两点分布、二项分布,根据它们的期望、方差公式计算.
2.期望(均值)仅体现了随机变量取值的平均水平
当我们希望实际的平均水平比较理想时,则先求它们的均值,但不要误认为均值相等时,它们都一样好,这时,还应看它们相对于均值的偏离程度,也就是看哪一个相对稳定(即计算方差的大小),稳定者就更好.如果我们希望比较稳定时,这时应先考虑方差,再考虑均值是否接近即可.
