3.1 独立性检验 课件(苏教版选修2-3)
文档属性
| 名称 | 3.1 独立性检验 课件(苏教版选修2-3) |  | |
| 格式 | zip | ||
| 文件大小 | 699.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-11 09:16:04 | ||
图片预览











文档简介
(共35张PPT)
3.1 独立性检验 课件(苏教版选修2-3)
课堂互动讲练
知能优化训练
3.1
课前自主学案
学习目标
学习目标
1.了解2×2列联表的意义.
2.了解随机变量χ2的意义.
3.通过典型案例分析了解独立性检验的基本思想和方法.
课前自主学案
温故夯基
简单随机抽样
系统抽样
分层抽样
0
知新益能
Ⅱ
类1 类2 合计
Ⅰ 类A a b a+b
类B c d c+d
合计 a+c b+d n=a+b+c+d
Ⅰ与Ⅱ没有关系
χ2
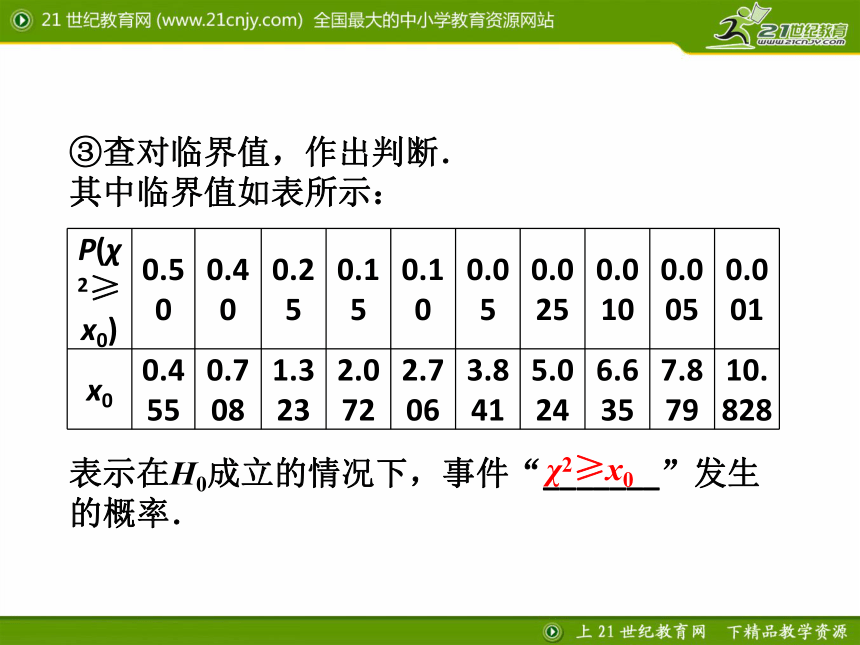
③查对临界值,作出判断.
其中临界值如表所示:
表示在H0成立的情况下,事件“_______”发生的概率.
P(χ2≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
χ2≥x0
3.变量独立性的判断
(1)如果____________ ,那么有99.9%的把握认为“Ⅰ与Ⅱ”有关系;
(2)如果____________ ,那么有99%的把握认为“Ⅰ与Ⅱ”有关系;
(3)如果____________ ,那么有90%的把握认为“Ⅰ与Ⅱ”有关系;
(4)如果____________ ,那么就认为没有充分的证据显示“Ⅰ与Ⅱ”有关系,但也不能作出结论“H0成立”,即Ⅰ与Ⅱ没有关系.
χ2>10.828
χ2>6.635
χ2>2.706
χ2≤2.706
问题探究
1.如何理解由χ2作出的判断?
提示:利用χ2进行独立性检验,可以对推断的正确性的概率作出估计,n越大,这个估计越准确.
2.在判断两变量相关时,若χ2=56.632,则P(χ2≥6.635)≈0.01和P(χ2≥10.828)≈0.001.
哪种说法是正确的?
提示:两种说法均正确.
P(χ2≥6.635)≈0.01的含义是:在犯错误的概率不超过0.01的前提下,认为两变量相关.
P(χ2≥10.828)≈0.001的含义是:在犯错误的概率不超过0.001的前提下,认为两变量相关.
课堂互动讲练
两个不独立事件的独立性检验
独立性检验的基本步骤:(1)找出相关数据,作出列联表;(2)求随机变量χ2的观测值;(3)比较临界值的大小,然后得出事件有关的可信程度.
考点突破
调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据表,试问能有多大把握认为婴儿的性别与出生时间有关系?
例1
出生时间
性别 晚上 白天 合计
男婴 24 31 55
女婴 8 26 34
合计 32 57 89
【名师点评】 研究两个变量是否独立的问题,其思路都是通过列联表的数据,计算统计量χ2,再和临界值对比得出认为它们有关系的把握程度,从而判断它们的独立性.
变式训练1 在国家未实施西部开发战略前,一新闻单位在应届大学毕业生中随机抽取1000人问卷,只有80人志愿加入西部建设.而国家实施西部开发战略后,随机抽取1200名应届大学毕业生问卷,有400人志愿加入国家西部建设.问实施西部开发战略是否对应届大学毕业生的选择产生了影响?
解:数据整理如下:
志愿者 非志愿者 合计
开发战略公布前 80 920 1000
开发战略公布后 400 800 1200
合计 480 1720 2200
两个独立事件的独立性检验
例2
(本题满分14分)研究人员选取170名青年男女大学生的样本,对他们进行一种心理测验,发现有60名女生对该心理测验中的最后一个题目的反应是:作肯定的18名,否定的42名;110名男生在相同的题目上作肯定的有22名,否定的有88名.问:性别与态度之间是否存在某种关系?用独立性检验的方法进行判断.
【思路点拨】 解答本题可先列出表格,然后计算χ2 ,再与临界值比较,判断两个变量是否相互独立.
【规范解答】 根据题目所给数据列出下列表格:
态度
性别 肯定 否定 合计
男生 22 88 110
女生 18 42 60
合计 40 130 170
【名师点评】 要熟练应用χ2公式,以免因公式不熟而导致结果错误.
变式训练2 某教育机构为了研究人具有大学专科以上学历(包括大学专科)和对待教育改革态度的关系,随机抽取了392名成年人进行调查,所得数据如下表所示:
对于教育机构的研究项目,根据上述数据能得出什么结论?
积极支持教育改革 不太赞成教育改革 合计
大学专科以上学历(包括大学专科) 39 157 196
大学专科以下学历 29 167 196
合计 68 324 392
独立性检验的应用
解决有关独立性检验的问题时,若题目中没有给出2×2列联表,需先根据题意画出2×2列联表,注意表中两个变量的放置位置,列表后可根据表中数据计算χ2的值,然后比较χ2值与临界值的大小来给出“两个变量”的相关性的判断.
例3
为研究学生对国家大事的关心与否与性别是否有关,在学生中随机抽样调查,结果如下:
(1)根据统计数据作出合适的判断分析;
(2)扩大样本容量,将表中每个数据扩大为原来的10倍,然后作出判断分析;
关心 不关心 合计
男生 182 18 200
女生 176 24 200
合计 358 42 400
(3)从某中学随机抽取450名学生,其中男、女生数量之比为5∶4,通过问卷调查发现男生关心国家大事的百分率为94%,而女生关心国家大事的百分率为85%,请根据这些数据,判断该中学的学生是否关心国家大事与性别的关系.
【思路点拨】 分别计算出三种情况下的χ2统计量的值,进行独立性检验,作出判断.
(3)依题意男、女生人数分别是250人和200人,男生中关心国家大事的人数为235人,女生中关心国家大事的人数为170人;
列出2×2列联表如下:
关心国家大事 不关心国家大事 合计
男生 235 15 250
女生 170 30 200
合计 405 45 450
【名师点评】 我们通过分析题意可求得χ2的值,根据χ2的值可以判断两个量是否有关系,并且能较精确地给出这种判断的可靠程度.三个不同的样本(包括样本量的不同)可能导致不同的结论或者影响判断正确(不正确)的程度.
变式训练3 网络对现代人的生活影响较大,尤其对青少年,为了解网络对中学生学习成绩的影响,某地区教育主管部门从辖区初中生中随机抽取了1000人调查,发现其中经常上网的有200人,这200人中有80人期末考试不及格,而另外800人中有120人不及格,问:中学生经常上网是否影响学习,为什么?
解:根据题意列出2×2列联表:
经常上网 不经常上网 合计
不及格 80 120 200
及格 120 680 800
合计 200 800 1000
方法感悟
1.画列联表时要把两个分类变量分别作为第一行和第一列,把数据填在相应的交叉点上,最右面一列为对行的合计,最下面一行为对列的合计.
2.对卡方公式要从结构上结合列联表记忆,分母分别是四个合计的积,分子是列联表主对角线之积与副对角线之积的差的平方再乘样本容量.注意:一是不要漏乘了样本容量,二是用公式时要细心计算,防止出错.
3.用卡方检验只能推定两类分类变量有多大程度的相关关系,而不能推定两个分类变量无关,所以当卡方的值小于2.706时,也不能对两个变量下“无关”的结论.
3.1 独立性检验 课件(苏教版选修2-3)
课堂互动讲练
知能优化训练
3.1
课前自主学案
学习目标
学习目标
1.了解2×2列联表的意义.
2.了解随机变量χ2的意义.
3.通过典型案例分析了解独立性检验的基本思想和方法.
课前自主学案
温故夯基
简单随机抽样
系统抽样
分层抽样
0
知新益能
Ⅱ
类1 类2 合计
Ⅰ 类A a b a+b
类B c d c+d
合计 a+c b+d n=a+b+c+d
Ⅰ与Ⅱ没有关系
χ2
③查对临界值,作出判断.
其中临界值如表所示:
表示在H0成立的情况下,事件“_______”发生的概率.
P(χ2≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
χ2≥x0
3.变量独立性的判断
(1)如果____________ ,那么有99.9%的把握认为“Ⅰ与Ⅱ”有关系;
(2)如果____________ ,那么有99%的把握认为“Ⅰ与Ⅱ”有关系;
(3)如果____________ ,那么有90%的把握认为“Ⅰ与Ⅱ”有关系;
(4)如果____________ ,那么就认为没有充分的证据显示“Ⅰ与Ⅱ”有关系,但也不能作出结论“H0成立”,即Ⅰ与Ⅱ没有关系.
χ2>10.828
χ2>6.635
χ2>2.706
χ2≤2.706
问题探究
1.如何理解由χ2作出的判断?
提示:利用χ2进行独立性检验,可以对推断的正确性的概率作出估计,n越大,这个估计越准确.
2.在判断两变量相关时,若χ2=56.632,则P(χ2≥6.635)≈0.01和P(χ2≥10.828)≈0.001.
哪种说法是正确的?
提示:两种说法均正确.
P(χ2≥6.635)≈0.01的含义是:在犯错误的概率不超过0.01的前提下,认为两变量相关.
P(χ2≥10.828)≈0.001的含义是:在犯错误的概率不超过0.001的前提下,认为两变量相关.
课堂互动讲练
两个不独立事件的独立性检验
独立性检验的基本步骤:(1)找出相关数据,作出列联表;(2)求随机变量χ2的观测值;(3)比较临界值的大小,然后得出事件有关的可信程度.
考点突破
调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据表,试问能有多大把握认为婴儿的性别与出生时间有关系?
例1
出生时间
性别 晚上 白天 合计
男婴 24 31 55
女婴 8 26 34
合计 32 57 89
【名师点评】 研究两个变量是否独立的问题,其思路都是通过列联表的数据,计算统计量χ2,再和临界值对比得出认为它们有关系的把握程度,从而判断它们的独立性.
变式训练1 在国家未实施西部开发战略前,一新闻单位在应届大学毕业生中随机抽取1000人问卷,只有80人志愿加入西部建设.而国家实施西部开发战略后,随机抽取1200名应届大学毕业生问卷,有400人志愿加入国家西部建设.问实施西部开发战略是否对应届大学毕业生的选择产生了影响?
解:数据整理如下:
志愿者 非志愿者 合计
开发战略公布前 80 920 1000
开发战略公布后 400 800 1200
合计 480 1720 2200
两个独立事件的独立性检验
例2
(本题满分14分)研究人员选取170名青年男女大学生的样本,对他们进行一种心理测验,发现有60名女生对该心理测验中的最后一个题目的反应是:作肯定的18名,否定的42名;110名男生在相同的题目上作肯定的有22名,否定的有88名.问:性别与态度之间是否存在某种关系?用独立性检验的方法进行判断.
【思路点拨】 解答本题可先列出表格,然后计算χ2 ,再与临界值比较,判断两个变量是否相互独立.
【规范解答】 根据题目所给数据列出下列表格:
态度
性别 肯定 否定 合计
男生 22 88 110
女生 18 42 60
合计 40 130 170
【名师点评】 要熟练应用χ2公式,以免因公式不熟而导致结果错误.
变式训练2 某教育机构为了研究人具有大学专科以上学历(包括大学专科)和对待教育改革态度的关系,随机抽取了392名成年人进行调查,所得数据如下表所示:
对于教育机构的研究项目,根据上述数据能得出什么结论?
积极支持教育改革 不太赞成教育改革 合计
大学专科以上学历(包括大学专科) 39 157 196
大学专科以下学历 29 167 196
合计 68 324 392
独立性检验的应用
解决有关独立性检验的问题时,若题目中没有给出2×2列联表,需先根据题意画出2×2列联表,注意表中两个变量的放置位置,列表后可根据表中数据计算χ2的值,然后比较χ2值与临界值的大小来给出“两个变量”的相关性的判断.
例3
为研究学生对国家大事的关心与否与性别是否有关,在学生中随机抽样调查,结果如下:
(1)根据统计数据作出合适的判断分析;
(2)扩大样本容量,将表中每个数据扩大为原来的10倍,然后作出判断分析;
关心 不关心 合计
男生 182 18 200
女生 176 24 200
合计 358 42 400
(3)从某中学随机抽取450名学生,其中男、女生数量之比为5∶4,通过问卷调查发现男生关心国家大事的百分率为94%,而女生关心国家大事的百分率为85%,请根据这些数据,判断该中学的学生是否关心国家大事与性别的关系.
【思路点拨】 分别计算出三种情况下的χ2统计量的值,进行独立性检验,作出判断.
(3)依题意男、女生人数分别是250人和200人,男生中关心国家大事的人数为235人,女生中关心国家大事的人数为170人;
列出2×2列联表如下:
关心国家大事 不关心国家大事 合计
男生 235 15 250
女生 170 30 200
合计 405 45 450
【名师点评】 我们通过分析题意可求得χ2的值,根据χ2的值可以判断两个量是否有关系,并且能较精确地给出这种判断的可靠程度.三个不同的样本(包括样本量的不同)可能导致不同的结论或者影响判断正确(不正确)的程度.
变式训练3 网络对现代人的生活影响较大,尤其对青少年,为了解网络对中学生学习成绩的影响,某地区教育主管部门从辖区初中生中随机抽取了1000人调查,发现其中经常上网的有200人,这200人中有80人期末考试不及格,而另外800人中有120人不及格,问:中学生经常上网是否影响学习,为什么?
解:根据题意列出2×2列联表:
经常上网 不经常上网 合计
不及格 80 120 200
及格 120 680 800
合计 200 800 1000
方法感悟
1.画列联表时要把两个分类变量分别作为第一行和第一列,把数据填在相应的交叉点上,最右面一列为对行的合计,最下面一行为对列的合计.
2.对卡方公式要从结构上结合列联表记忆,分母分别是四个合计的积,分子是列联表主对角线之积与副对角线之积的差的平方再乘样本容量.注意:一是不要漏乘了样本容量,二是用公式时要细心计算,防止出错.
3.用卡方检验只能推定两类分类变量有多大程度的相关关系,而不能推定两个分类变量无关,所以当卡方的值小于2.706时,也不能对两个变量下“无关”的结论.
