第1章 本章优化总结 课件(苏教版选修2-3)
文档属性
| 名称 | 第1章 本章优化总结 课件(苏教版选修2-3) |

|
|
| 格式 | zip | ||
| 文件大小 | 680.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-11 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第1章 本章优化总结 课件(苏教版选修2-3)
专题探究精讲
本章优化总结
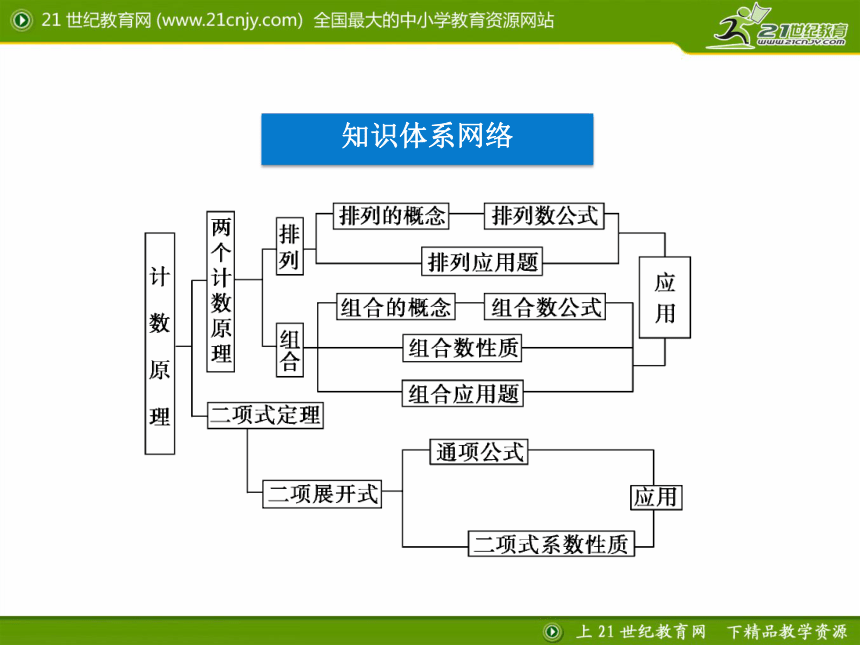
知识体系网络
章末综合检测
知识体系网络
专题探究精讲
两个计数原理的应用
分类计数原理和分步计数原理是本章内容的基础.在应用题的考查中,经常要用它对问题进行分类或分步分析求解,如何灵活利用这两个原理对问题进行分类或分步往往是解应用题的关键.
车间有11名工人,其中5名男工是钳工,4名女工是车工,另外两名老师傅既能当车工又能当钳工,现在要在这11名工人里选派4名钳工,4名车工修理一台机床,有多少种选派方法?
【分析】 两名老师傅既能当车工又能当钳工称之为“多面手”,因此应做到对这两名老师傅进行恰当、合理的分类.
例1
【名师点评】 法一是以老师傅为主考虑的;法二是以钳工为主考虑的;法三是以车工为主考虑的.本题中的“多面手”,可称为“特殊对象”,在解题中按“特殊对象”进行分类是常用的方法,要注意分类的独立性.
排列、组合的应用
在解决一个实际问题的过程中,常常遇到排列、组合的综合性问题.而解决问题的第一步是审题,只有认真审题,才能把握问题的实质,分清是排列问题、组合问题,还是综合问题,分清分类与分步的标准和方式,并且要遵循两个原则:一是按元素的性质进行分类;二是按事情发生的过程进行分步.
一条长椅上有七个座位,四个人坐,要求三个空位中,有两个空位相邻,另一个空位与这两个相邻空位不相邻,共有几种坐法?
【分析】 先把两个相邻空位看成一个整体,与另一个空位看作两个元素插入另外四个座位产生的五个空当中,即可解决问题.
例2
【名师点评】 优先安排人入坐,再让空位去“插队”,使问题得解.
例3
把4个男学生和4个女学生平均分成4组,到4辆公共汽车里参加售票体验活动,且同样两人在不同汽车上服务算作不同情况.
(1)有几种不同的分配方法?
(2)男学生与女学生分别分组,有几种不同的分配方法?
(3)每个小组必须是一个男学生和一个女学生,有几种不同的分配方法?
【分析】 本题考查的是排列组合的综合问题.(1)是平均分配问题.(2)先排列男、女学生,再用分步计数原理求解.(3)先把男、女学生分别分组,再排列.
【名师点评】 由本题可以看出对一个具体问题,用排列也好,组合也好,用分步计数原理还是用分类计数原理,都需要对具体问题进行具体分析,看是否与元素顺序有关,再选择分类或分步,并且做到元素不重不漏,这是解决排列组合问题的关键.
例4
由1,2,3,4,5这五个数字组成没有重复数字的五位数并排成一个递增数例,则首项为12345,第2项是12354,…直到末项(第120项)是54321.
(1)43251是第几项?
(2)第93项是怎样的一个五位数?
【分析】 (1)43251前面的数都比43251小,而后面的数都比43251大,因此比43251小的数的个数加1就是43251的项数,反过来,从总个数中减去比43251大的数的个数也是43251的项数.(2)先算出比第93项大的数的个数,从总个数中减去此数,再从万位数是5的个数,逐步缩小直到第93项的数为止,从而得到第93项的那个数.
【名师点评】 对于两个基本计数原理,在排列组合的学习与运用中要注意分类讨论、等价转换、整体思想、正难则反等数学思想的运用.
二项式定理及应用
二项式定理是历年高考中的必考内容,解决二项式定理问题,特别是涉及求二项展开式的通项的问题,关键在于抓住通项公式,还要注意区分“二项式系数”与“展开式系数”.
二项式定理的应用主要有以下几个方面:
(1)近似求值.利用二项式定理进行近似计算,关键在于构造恰当的二项式(p+q)n,(其中|q|<1),并根据近似要求,对展开式的项合理取舍.
(2)解决整除问题.通常把底数化为两数的和或差的形式,且这种转化形式与除数有密切的关系,再利用二项式定理展开,只考虑前面或后面的一两项就可以.
(3)求和.求二项展开式系数和的基本方法是赋值法.在解决有些数列求和的问题时,要注意对问题实施转化,为应用二项式定理创造条件.
(4)解不等式或证明组合恒等式.用二项式定理证明不等式时,通常表现为二项式定理的正用或逆用,再结合不等式的证明方法论证.而证明组合恒等式的关键在于构造不同的二项式,比较系数进行证明.
例5
已知(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11,那么a1+a2+a3+…+a11=________.
【分析】 令x=1与x=0即可解决问题.
【解析】 令x=0,得a0=1;
令x=1,得a0+a1+a2+…+a11=-64;
∴a1+a2+…+a11=-65.
【答案】 -65
【名师点评】 赋值法是求二项式系数和的主要方法.
例6
【分析】 本题是应用二项式定理通项公式的典型问题,解答本题的关键是利用方程思想列出方程,求出n.
【名师点评】 正确写出二项展开式的通项是解题的关键.
第1章 本章优化总结 课件(苏教版选修2-3)
专题探究精讲
本章优化总结
知识体系网络
章末综合检测
知识体系网络
专题探究精讲
两个计数原理的应用
分类计数原理和分步计数原理是本章内容的基础.在应用题的考查中,经常要用它对问题进行分类或分步分析求解,如何灵活利用这两个原理对问题进行分类或分步往往是解应用题的关键.
车间有11名工人,其中5名男工是钳工,4名女工是车工,另外两名老师傅既能当车工又能当钳工,现在要在这11名工人里选派4名钳工,4名车工修理一台机床,有多少种选派方法?
【分析】 两名老师傅既能当车工又能当钳工称之为“多面手”,因此应做到对这两名老师傅进行恰当、合理的分类.
例1
【名师点评】 法一是以老师傅为主考虑的;法二是以钳工为主考虑的;法三是以车工为主考虑的.本题中的“多面手”,可称为“特殊对象”,在解题中按“特殊对象”进行分类是常用的方法,要注意分类的独立性.
排列、组合的应用
在解决一个实际问题的过程中,常常遇到排列、组合的综合性问题.而解决问题的第一步是审题,只有认真审题,才能把握问题的实质,分清是排列问题、组合问题,还是综合问题,分清分类与分步的标准和方式,并且要遵循两个原则:一是按元素的性质进行分类;二是按事情发生的过程进行分步.
一条长椅上有七个座位,四个人坐,要求三个空位中,有两个空位相邻,另一个空位与这两个相邻空位不相邻,共有几种坐法?
【分析】 先把两个相邻空位看成一个整体,与另一个空位看作两个元素插入另外四个座位产生的五个空当中,即可解决问题.
例2
【名师点评】 优先安排人入坐,再让空位去“插队”,使问题得解.
例3
把4个男学生和4个女学生平均分成4组,到4辆公共汽车里参加售票体验活动,且同样两人在不同汽车上服务算作不同情况.
(1)有几种不同的分配方法?
(2)男学生与女学生分别分组,有几种不同的分配方法?
(3)每个小组必须是一个男学生和一个女学生,有几种不同的分配方法?
【分析】 本题考查的是排列组合的综合问题.(1)是平均分配问题.(2)先排列男、女学生,再用分步计数原理求解.(3)先把男、女学生分别分组,再排列.
【名师点评】 由本题可以看出对一个具体问题,用排列也好,组合也好,用分步计数原理还是用分类计数原理,都需要对具体问题进行具体分析,看是否与元素顺序有关,再选择分类或分步,并且做到元素不重不漏,这是解决排列组合问题的关键.
例4
由1,2,3,4,5这五个数字组成没有重复数字的五位数并排成一个递增数例,则首项为12345,第2项是12354,…直到末项(第120项)是54321.
(1)43251是第几项?
(2)第93项是怎样的一个五位数?
【分析】 (1)43251前面的数都比43251小,而后面的数都比43251大,因此比43251小的数的个数加1就是43251的项数,反过来,从总个数中减去比43251大的数的个数也是43251的项数.(2)先算出比第93项大的数的个数,从总个数中减去此数,再从万位数是5的个数,逐步缩小直到第93项的数为止,从而得到第93项的那个数.
【名师点评】 对于两个基本计数原理,在排列组合的学习与运用中要注意分类讨论、等价转换、整体思想、正难则反等数学思想的运用.
二项式定理及应用
二项式定理是历年高考中的必考内容,解决二项式定理问题,特别是涉及求二项展开式的通项的问题,关键在于抓住通项公式,还要注意区分“二项式系数”与“展开式系数”.
二项式定理的应用主要有以下几个方面:
(1)近似求值.利用二项式定理进行近似计算,关键在于构造恰当的二项式(p+q)n,(其中|q|<1),并根据近似要求,对展开式的项合理取舍.
(2)解决整除问题.通常把底数化为两数的和或差的形式,且这种转化形式与除数有密切的关系,再利用二项式定理展开,只考虑前面或后面的一两项就可以.
(3)求和.求二项展开式系数和的基本方法是赋值法.在解决有些数列求和的问题时,要注意对问题实施转化,为应用二项式定理创造条件.
(4)解不等式或证明组合恒等式.用二项式定理证明不等式时,通常表现为二项式定理的正用或逆用,再结合不等式的证明方法论证.而证明组合恒等式的关键在于构造不同的二项式,比较系数进行证明.
例5
已知(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11,那么a1+a2+a3+…+a11=________.
【分析】 令x=1与x=0即可解决问题.
【解析】 令x=0,得a0=1;
令x=1,得a0+a1+a2+…+a11=-64;
∴a1+a2+…+a11=-65.
【答案】 -65
【名师点评】 赋值法是求二项式系数和的主要方法.
例6
【分析】 本题是应用二项式定理通项公式的典型问题,解答本题的关键是利用方程思想列出方程,求出n.
【名师点评】 正确写出二项展开式的通项是解题的关键.
