2021-2022学年华东师大版数学九年级上册23.1.1 成比例线段课件(20张)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级上册23.1.1 成比例线段课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 21:42:28 | ||
图片预览






文档简介
(共20张PPT)
23.1.
成比例线段
第23章
图形的相似
第一课时
成比例线段
学习目标
1.掌握相似图形的概念;(重点)
2.了解成比例线段,比例的基本性质;
(重点)
3.能根据比例的基本性质解决相关问题.(难点)
一、相似图形的概念
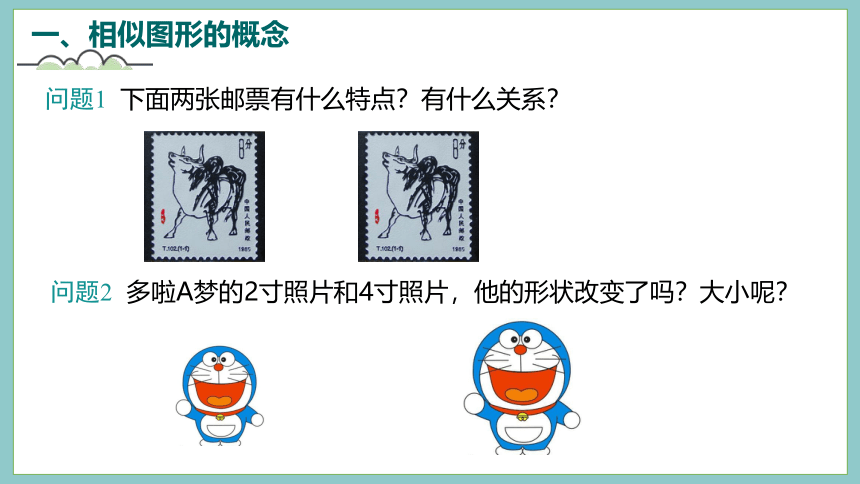
问题1
下面两张邮票有什么特点?有什么关系?
问题2
多啦A梦的2寸照片和4寸照片,他的形状改变了吗?大小呢?
下面图形有什么相同和不同的地方?
一、相似图形的概念
相同点:形状相同.
不同点:大小不相同.
形状相同的图形叫做相似图形.
注意:相似图形的大小不一定相同.
相似图形的概念
二、线段的比及比例线段
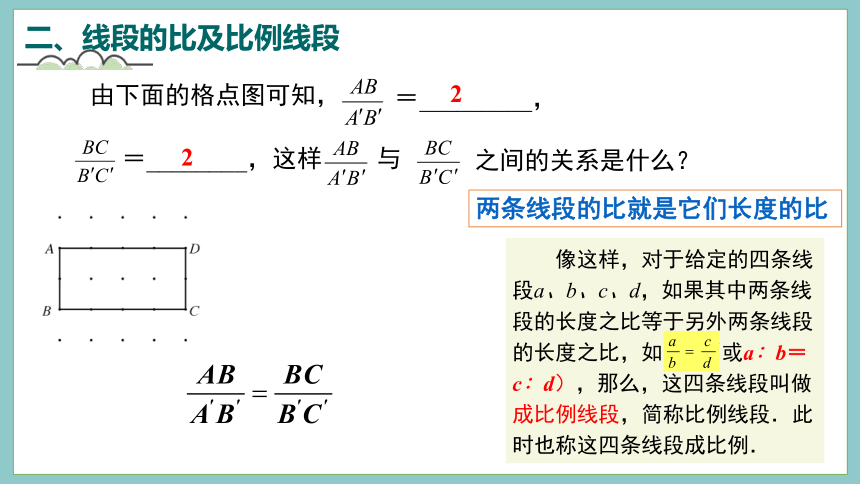
由下面的格点图可知,
=_________,
=________,这样
与
之间的关系是什么?
2
2
像这样,对于给定的四条线段a、b、c、d,如果其中两条线段的长度之比等于另外两条线段的长度之比,如
(或a∶b=c∶d),那么,这四条线段叫做成比例线段,简称比例线段.此时也称这四条线段成比例.
两条线段的比就是它们长度的比
用a,b,c,d
表示四条线段,则a,b,c,d
成比例线段可写成怎样的形式?
或
a:b=c:d,
那么
a、b、c、d
叫做组成比例的项,
a、d
叫做比例外项,
b、c
叫做比例内项,
d
叫做
a、b、c的第四比例项.
特殊情况:若作为比例内项的两条线段相等,即a:b=b:c,则b叫做a,c的比例中项.
二、线段的比及比例线段
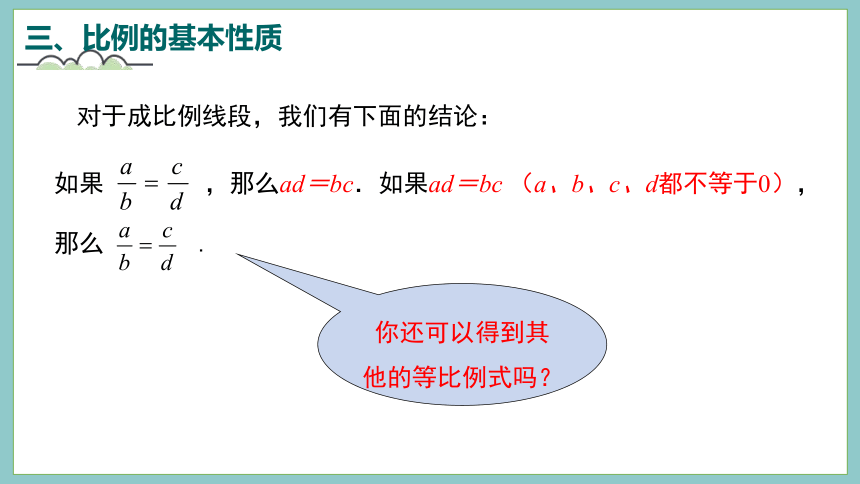
如果
,那么ad=bc.如果ad=bc
(a、b、c、d都不等于0),那么
.
对于成比例线段,我们有下面的结论:
你还可以得到其他的等比例式吗?
三、比例的基本性质
典例分析
例1:判断下列线段a、b、c、d是否是成比例线段.
(1)a=4,b=8,c=5,d=10;
(2)a=2,b=
,c=
,d=
.
练习巩固
1.判断下列线段是不是成比例线段:
(1)2cm,
4cm,
3cm,
8cm;
(2)2cm,
4cm,
3m,
6m;
(3)1.2dm,
3cm,
20cm,
0.5m;
(5)1m,
3m,
3m,
9m.
特殊情况:若x:y=y:z,则y叫做x,z的比例中项.
2.已知:线段a、b、c满足关系式
且b=4,那么ac=______.
16
练习
1.若a,b,c,d是成比例线段,其中a=5
cm,b=3
cm,c=2
cm,
则线段d=_____cm.
3.如果数b是a、c的比例中项,且a=8,c=6,那么b=
.
练习
4.已知
,那么下列式子中一定成立的是___________
①x+y=5
②2y=3x
③
④
5.已知
,则
的值为_________
6.如果a∶b=3∶4,c∶b=4∶3,那么a∶b∶c等于___________
练习
7.若
____.
8.若x∶y∶z=2∶4∶5,求
的值.
解题方法:见比设参
典例分析
例2:
证明:(1)如果
,那么
证明:(1)∵
在等式两边同加上1,
∴
∴
(法一)
典例分析
(2)如果
,那么
(其中a≠b,c≠d).
∴ ad=bc,
∴
-
ad=
-
bc,
在等式两边同加上ac,
∴ ac-ad=ac-bc,
∴ a(c-d)=(a-b)c,
两边同除以(a-b)(c-d),
证明: ∵
.
∴
拓展归纳
合比性质:
等比性质:
练习
,那么
、
各等于多少?
1.已知
练习
练习
求a:b:c的值.
课堂小结
1.若线段a,b,c,d满足
,则a,b,c,d叫做成比例线段,简称比例线段.
2.
把b叫做a,c的比例中项;
3.常用方法:见比设参,即设一份为k;
4.比例的基本性质:
合比性质:
等比性质:
完毕·感谢
The
user
can
perform
the
presentation
on
a
projector
or
computer,
and
the
powerpoint
can
be
printed
out
and
made
into
film.
23.1.
成比例线段
第23章
图形的相似
第一课时
成比例线段
学习目标
1.掌握相似图形的概念;(重点)
2.了解成比例线段,比例的基本性质;
(重点)
3.能根据比例的基本性质解决相关问题.(难点)
一、相似图形的概念
问题1
下面两张邮票有什么特点?有什么关系?
问题2
多啦A梦的2寸照片和4寸照片,他的形状改变了吗?大小呢?
下面图形有什么相同和不同的地方?
一、相似图形的概念
相同点:形状相同.
不同点:大小不相同.
形状相同的图形叫做相似图形.
注意:相似图形的大小不一定相同.
相似图形的概念
二、线段的比及比例线段
由下面的格点图可知,
=_________,
=________,这样
与
之间的关系是什么?
2
2
像这样,对于给定的四条线段a、b、c、d,如果其中两条线段的长度之比等于另外两条线段的长度之比,如
(或a∶b=c∶d),那么,这四条线段叫做成比例线段,简称比例线段.此时也称这四条线段成比例.
两条线段的比就是它们长度的比
用a,b,c,d
表示四条线段,则a,b,c,d
成比例线段可写成怎样的形式?
或
a:b=c:d,
那么
a、b、c、d
叫做组成比例的项,
a、d
叫做比例外项,
b、c
叫做比例内项,
d
叫做
a、b、c的第四比例项.
特殊情况:若作为比例内项的两条线段相等,即a:b=b:c,则b叫做a,c的比例中项.
二、线段的比及比例线段
如果
,那么ad=bc.如果ad=bc
(a、b、c、d都不等于0),那么
.
对于成比例线段,我们有下面的结论:
你还可以得到其他的等比例式吗?
三、比例的基本性质
典例分析
例1:判断下列线段a、b、c、d是否是成比例线段.
(1)a=4,b=8,c=5,d=10;
(2)a=2,b=
,c=
,d=
.
练习巩固
1.判断下列线段是不是成比例线段:
(1)2cm,
4cm,
3cm,
8cm;
(2)2cm,
4cm,
3m,
6m;
(3)1.2dm,
3cm,
20cm,
0.5m;
(5)1m,
3m,
3m,
9m.
特殊情况:若x:y=y:z,则y叫做x,z的比例中项.
2.已知:线段a、b、c满足关系式
且b=4,那么ac=______.
16
练习
1.若a,b,c,d是成比例线段,其中a=5
cm,b=3
cm,c=2
cm,
则线段d=_____cm.
3.如果数b是a、c的比例中项,且a=8,c=6,那么b=
.
练习
4.已知
,那么下列式子中一定成立的是___________
①x+y=5
②2y=3x
③
④
5.已知
,则
的值为_________
6.如果a∶b=3∶4,c∶b=4∶3,那么a∶b∶c等于___________
练习
7.若
____.
8.若x∶y∶z=2∶4∶5,求
的值.
解题方法:见比设参
典例分析
例2:
证明:(1)如果
,那么
证明:(1)∵
在等式两边同加上1,
∴
∴
(法一)
典例分析
(2)如果
,那么
(其中a≠b,c≠d).
∴ ad=bc,
∴
-
ad=
-
bc,
在等式两边同加上ac,
∴ ac-ad=ac-bc,
∴ a(c-d)=(a-b)c,
两边同除以(a-b)(c-d),
证明: ∵
.
∴
拓展归纳
合比性质:
等比性质:
练习
,那么
、
各等于多少?
1.已知
练习
练习
求a:b:c的值.
课堂小结
1.若线段a,b,c,d满足
,则a,b,c,d叫做成比例线段,简称比例线段.
2.
把b叫做a,c的比例中项;
3.常用方法:见比设参,即设一份为k;
4.比例的基本性质:
合比性质:
等比性质:
完毕·感谢
The
user
can
perform
the
presentation
on
a
projector
or
computer,
and
the
powerpoint
can
be
printed
out
and
made
into
film.
