第四章 《图形的相似》检测卷(含解析)
文档属性
| 名称 | 第四章 《图形的相似》检测卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 186.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 00:00:00 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
广东省佛山市高明区2021-2022学年度北师大版九年级上册
第四章《图形的相似》检测卷
一、选择题(每小题3分,共30分)
1.下列四组线段中,不能成比例的是(??
)
A.?a=3,b=6,c=2,d=4???????
????????B.?a=1,b=3,c=2,d=6
C.?a=4,b=6,c=5,d=10????????????????????????????????D.?a=2,b=5,c=4,d=10
2.如果5x=6y,那么下列结论正确的是(?
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
3.如图,
ABC中,点D、E分别在AB、AC上,且
,下列结论正确的是(??
)
A.?DE:BC=1:2???????????????????????????????????????????????????B.?
ADE与
ABC的面积比为1:3
C.?
ADE与
ABC的周长比为1:2??????????????????D.?DE
BC
4.用一个10倍的放大镜去观察一个三角形,下列说法中正确的是(??
)
①三角形的每个角都扩大10倍;②三角形的每条边都扩大10倍;
③三角形的面积扩大10倍;④三角形的周长扩大10倍.
A.?①②??????????????????B.?①③??????????????????????C.?②④???????????
???D.?②③
5.如图,□ABCD中,EF∥AB,DE∶DA
=
2∶5,EF
=
4,则CD的长为(???
)
A.
B.8
C.10
D.16
6.如图,
和
是位似三角形,位似中心为点
,
,则
和
的位似比为(??
)
A.???????????????????????????????B.?????????????????????????????C.??????????????????????????????????D.?
7.如图,
、
交于
点,
,则下列结论一定正确的是(???
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
8.如图,△ABC是一张锐角三角形的纸片,AD是边BC上的高,已知BC=20cm,AD=15cm,从这张纸片上剪一下一个矩形,使矩形的一边在BC上,另两个顶点分别在AB、AC上。则下列结论不正确的是(
???)
A.?当△AHG的面积等于矩形面积时,HE的长为5cm
B.?当HE的长为6cm时,剪下的矩形的边HG是HE的2倍
C.?当矩形的边HG是HE的2倍时,矩形面积最大
D.?当矩形的面积最大时,HG的长是10cm
9.如图,在平行四边形
中,F是
上一点,且
,连结
并延长交
的延长线于点G
,
则
的值为(
??)
A.???????????????????????????????B.????????????????????????????????C.????????????????????????????D.?
10.如图,正方形
中,点
是
边上一点,连接
,以
为对角线作正方形
,边
与正方形
的对角线
相交于点
,连接
.以下四个结论:①
;②
;③
;④
.其中正确的个数为(??
)
A.?1个?????????????????????????B.?2个??????????????????????????C.?3个????????????????????????D.?4个
二、填空题(每小题4分,共28分)
11.已知
,则
=________.
12.在某一时刻,测得一根高为1.5
m的竹竿的影长为3
m,同时同地测得一栋楼的影长为60
m,则这栋楼的高度为________m.
13.在平面直角坐标系中,点
的坐标为
,点
的坐标为
,在第三象限内作与
位似的
,点
的对应点为点
,
与
的位似比为
,则点
的坐标为________.
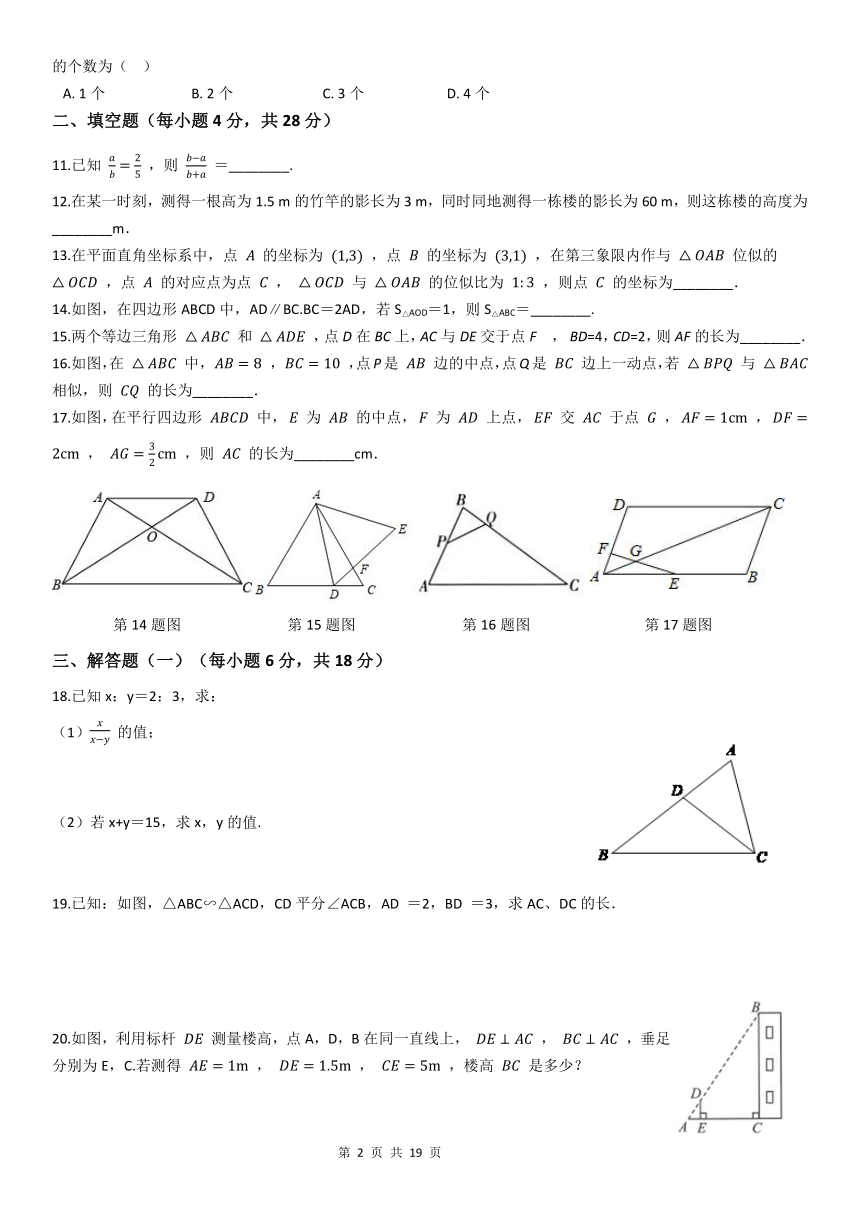
14.如图,在四边形ABCD中,AD∥BC.BC=2AD,若S△AOD=1,则S△ABC=________.
15.两个等边三角形
和
,点D在BC上,AC与DE交于点F
,
BD=4,CD=2,则AF的长为________.
16.如图,在
中,
,
,点P是
边的中点,点Q是
边上一动点,若
与
相似,则
的长为________.
17.如图,在平行四边形
中,
为
的中点,
为
上点,
交
于点
,
,
,
,则
的长为________cm.
第14题图
第15题图
第16题图
第17题图
三、解答题(一)(每小题6分,共18分)
18.已知x:y=2:3,求:
(1)
的值;
(2)若x+y=15,求x,y的值.
19.已知:如图,△ABC∽△ACD,CD平分∠ACB,AD
=2,BD
=3,求AC、DC的长.
20.如图,利用标杆
测量楼高,点A,D,B在同一直线上,
,
,垂足分别为E,C.若测得
,
,
,楼高
是多少?
四、解答题(二)(每小题8分,共24分)
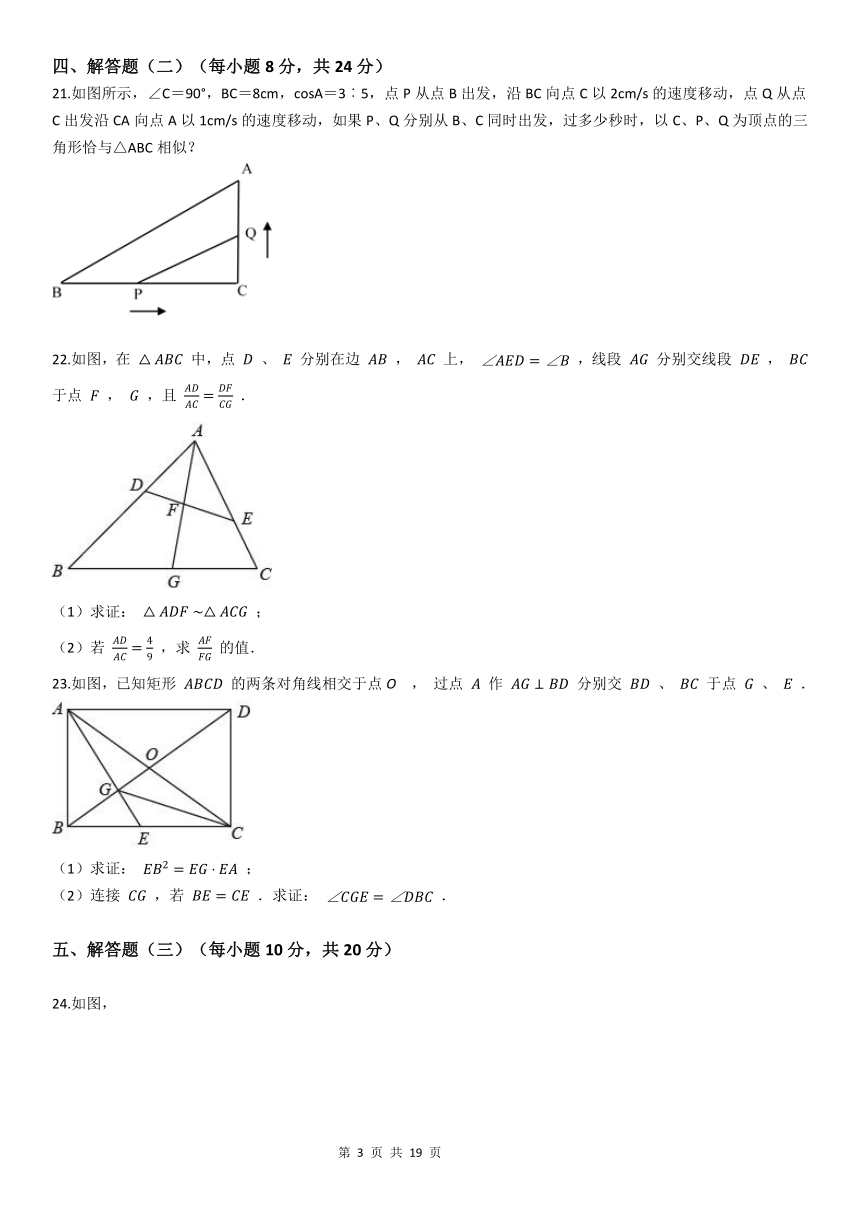
21.如图所示,∠C=90°,BC=8cm,cosA=3︰5,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
22.如图,在
中,点
、
分别在边
,
上,
,线段
分别交线段
,
于点
,
,且
.
(1)求证:
;
(2)若
,求
的值.
23.如图,已知矩形
的两条对角线相交于点O
,
过点
作
分别交
、
于点
、
.
(1)求证:
;
(2)连接
,若
.求证:
.
五、解答题(三)(每小题10分,共20分)
24.如图,
(1)【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G.
求证:
.
(2)【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若
,
,求线段DE的长.
(3)【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若
,
,求
的值(用含k的代数式表示).
25.已知:如图,在矩形ABCD中,AB=24cm,BC=16cm,点E为边CD的中点,连接BE
,
EF⊥BE交AD于点F
.
点P从点B出发,沿BE方向匀速运动,速度为2cm/s;同时,点Q从点A出发,沿AB方向匀速运动,速度为3cm/s.当一个点停止运动时,另一个点也停止运动.设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,点P在线段BQ的垂直平分线上?
(2)连接PQ
,
设五边形AFEPQ的面积为y(cm2),求y与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t
,
使S五边形AFEPQ∶S矩形ABCD=33∶64?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t
,
使点Q在∠AFE的平分线上?若存在,求出t的值;若不存在,请说明理由.
答案解析部分
一、选择题(每小题3分,共30分)
1.【答案】
C
【解析】【解答】解:A、∵2×6=3×4,∴四组线段中能成比例;不符合题意;
B、∵1×6=3×2,∴四组线段中能成比例;不符合题意;
C、∵4×10≠5×6,∴四组线段中不能成比例;符合题意;
D、∵2×10=4×10,∴四组线段中能成比例;不符合题意;
故答案为:C.
【分析】根据比例的性质验证四条线段是否两两乘积相等即可判断求解.
2.【答案】
A
【解析】【解答】A,
可以得出:
故答案为:A.
【分析】根据两内项之积等于两外项之积可判断求解.
3.【答案】
D
【解析】【解答】解:∵
,
∴AD:AB=AE:AC=1:3,
∵∠A=∠A,
∴△ADE∽△ABC,
∴DE:BC=1:3,故A错误;
∵△ADE∽△ABC,
∴△ADE与△ABC的面积比为1:9,周长的比为1:3,故B和C错误;
∵△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.故D正确.
故答案为:D.
【分析】由已知条件可得AD:AB=AE:AC=1:3,证明△ADE∽△ABC,由相似三角形的性质可判断A、B、C;由相似三角形对应角相等可得∠ADE=∠B,利用平行线的判定定理可判断D.
4.【答案】
C
【解析】【解答】解:①三角形的每个角不会变化,故错误;
②三角形的每条边都扩大10倍,故正确;
③三角形的面积会扩大100倍,故错误;
④三角形的周长会扩大10倍,故正确.
故答案为:C.
【分析】①由三角形的内角和等于180°可知,用一个10倍的放大镜去观察一个三角形,三角形的每个角不会变化;
②三角形的每条边都扩大10倍;
③根据S△=底×高可知,三角形的面积会扩大100倍;
④三角形的周长会扩大10倍.
5.【答案】
C
【解析】【解答】∵EF∥AB
∴△DEF∽△DAB
∴
∴AB=10
∴CD=AB=10
故答案为:C.
【分析】先证明△DEF∽△DAB,再求出
,
最后计算求解即可。
6.【答案】
D
【解析】【解答】解:∵
,
∴
,
∴
和
的位似比为
,
故答案为:D.
【分析】利用位似图形的性质即可求解.
7.【答案】
C
【解析】【解答】解:
,
,
,故A不符合题意,
,
,
,
,故B不符合题意,
,
,
,
,
,故C符合题意,
,
,
,
,故D不符合题意.
故答案为:C.
【分析】先求出△AEO△ABC,再根据
?和相似三角形的性质对每个选项一一判断即可。
8.【答案】
C
【解析】【解答】解:A.∵
△AHG的面积等于矩形面积,
∴HG·AP=HG·PD,
∴AP=PD,
∴(15-PD)=PD,
∴HE=PD=5(cm),
故A正确;
B.∵△AHG∽△ABC,
∴
,
∴
,
∴HG=12=2HE,
故B正确;
C.
∵△AHG∽△ABC,
∴
,
∴
,
解得:HG=20-HE,
∴S矩形=HG·HE=(20-HE)·HE=-HE2+20HE=-(HE-)2+75,
∴当HE=-时,
S矩形最大,
∴HG=20-HE=10(cm),
故C不正确,D正确.
故答案为:C.
【分析】A.根据三角形的面积和矩形的面积公式列出等式,得出(15-PD)=PD,求出PD的长,即可求出HE的长,从而判断A正确;
B.先证出△AEF∽△ABC,列出比例式,得出
,
求出HG的长,即可判断B正确;
CD.根据△AHG∽△ABC,得出
,
得出HG=20-HE,进而得出矩形EFHG的面积为-(HE-)2+75,利用二次函数的性质得出当HE=-时,
S矩形最大,再求出HG的长,即可判断C不正确,D正确.
9.【答案】
C
【解析】【解答】解:根据题意,
∵四边形
是平行四边形,
∴AB∥CD
,
∴△ABF∽△DGF
,
∴
,
∴
,
∴
,
∴
,
∵AB∥CD
,
∴△ABE∽△CGE,
∴
;
故答案为:C.
【分析】由四边形
是平行四边形,可证出△ABF∽△DGF
,
再利用平行线分线段成比例的了即可解决问题。
10.【答案】
D
【解析】【解答】解:①∵四边形AEFG和四边形ABCD均为正方形
∴∠EAG=∠BAD=90°
又∵∠EAB=90°-∠BAG,∠GAD=90°-∠BAG
∴∠EAB=∠GAD
∴①正确②∵四边形AEFG和四边形ABCD均为正方形
∴AD=DC,AG=FG
∴AC=
AD,AF=
AG
∴
,
即
又∵∠DAG+∠GAC=∠FAC+∠GAC
∴∠DAG=∠CAF
∴
∴②正确③∵四边形AEFG和四边形ABCD均为正方形,AF、AC为对角线
∴∠AFH=∠ACF=45°
又∵∠FAH=∠CAF
∴△HAF∽△FAC
∴
即
又∵AF=
AE
∴
∴③正确④由②知
又∵四边形ABCD为正方形,
AC为对角线
∴∠ADG=∠ACF=45°
∴DG在正方形另外一条对角线上
∴DG⊥AC
∴④正确
故答案为:D.
【分析】根据正方形的性质可得∠EAG=∠BAD=90°,利用同角的余角相等可得∠EAB=∠GAD,据此判断①;根据两组对边成比例且夹角相等,可证
,
据此判断②;先证△HAF∽△FAC,可得
,
可得
,
由AF=
AE,即得
,
据此判断③;由
,
可得∠ADG=∠ACF=45°,从而求出∠AND=90°,据此判断④.
二、填空题(每小题4分,共28分)
11.【答案】
【解析】【解答】解:∵
∴
设
=k,则a=2k,b=5k
∴
.
故填
.
【分析】
12.【答案】
30
【解析】【解答】解:设这栋楼的高度为hm,
∵在某一时刻,测得一根高为1.5m的竹竿的影长为3m,同时测得一栋楼的影长为60m,
∴
=
,
解得h=30.
故答案为:30.
【分析】先求出
=
,再解方程即可。
13.【答案】
【解析】【解答】解:∵
与
位似,点
的对应点为点
,
与
的位似比为
,
∵点
的坐标为
,点
在第三象限内,
∴点
的横纵坐标分别为:
,
;
∴点
的坐标为
;
故答案为:
;
【分析】根据相似和点C所在的象限求解即可。
14.【答案】
6
【解析】【解答】解:∵四边形ABCD中,AD//BC.
∴△AOD∽△COB.
∵AD
=
2BC.
∴AD:BC=1:2,
∴OD:OB=AD:BC=1:2,S△BOC=4
S△AOD=4
∴S△AOD:S△AOB
=1:2,即S△AOB
=2
∴S△ABC=S△BOC+
S△AOB
=4+2=6.
故填6.
【分析】
15.【答案】
【解析】【解答】∵
和
都是等边三角形,BD=4,CD=2,
∴AB=AC=BC=6,∠B=∠C=∠ADF=60°,
∴∠ADB+∠BAD=∠ADB+∠CDF=120°,
∴∠BAD=∠CDF,
∴
,
∴
,即
,
解得
,
∴
,
故答案为:
.
【分析】先求出∠BAD=∠CDF,再求出
,
最后计算求解即可。
16.【答案】
5或
【解析】【解答】∵
,
,点P是
边的中点
∴
当
时
∴
即
解得:
∴
当
时
∴
即
解得:
∴
∴
或
故答案为:
或
.
【分析】利用
或者
,分别得出答案。
17.【答案】
7.5
【解析】【解答】过点E作
,交AC于点H,如下图:
∵
∴
又∵
∴
∴
又∵四边形
是平行四边形,
且
为
的中点,
∴
,
,
∵
,
∴
,
∴
,
∴
cm.
故答案为:7.5
【分析】过点E做EH//AD,构造相似三角形,由相似性质得对应线段成比例,因为
且
为
的中点,由中位线推论得:EH是△ABC的中位线,因此。已知AF=1,DF=2,所以,因此,综合看,因此,
,
所以
,
AC=2AH=
三、解答题(一)(每小题6分,共18分)
18.【答案】
(1)解:
=
=﹣2
(2)解:∵x+y=15,
∴2k+3k=15,
解得:k=3,
∴x=6,y=9
【解析】【分析】(1)由已知的比例式可设x=2k,y=3k;(1)把x、y的值代入代数式计算即可求解;
(2)把x、y的值代入等式x+y=15可得关于k的方程,解方程可求得k的值,则x、y的值可求解.
?
?
19.【答案】
证明:
如图
∵△ABC∽△ACD,
∴∠1=∠B,
又∵CD是平分∠ACB,
∴∠1=∠2,
∴∠2=∠B,
∴BD=DC.
∵BD=3,
∴DC=3;
又∵AD
=2,BD
=3,
∴AB=5
由
得
即
=2×5=10
∴
.
【解析】【分析】利用相似三角形的性质得到
∠1=∠B,?
,把已知数据代入比例式求解即可得到AC的长;再结合角平分线的性质、等腰三角形的判定可求出DC的长。
20.【答案】
解:∵
,
,
∴
m,
∵
,
,
∴
∥
,
∴△ADE∽△ABC,
∴
,
∵
,
∴
,
∴
;
∴楼高
是9米.
【解析】【分析】由??,?
,
可得?∥?
,
可证△ADE∽△ABC,可得
,
代入相应数据,即可求出BC.
四、解答题(二)(每小题8分,共24分)
21.【答案】
解:∵∠C=90°,cosA=3︰5,
∴
,
∵BC=8cm,
∴
,
,
∵点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,设运动时间为t秒,则有:
,
∴
,
①当
时,则
,
∴
,即
,
解得:
,
②当
时,则
,
∴
,即
,
解得:
;
综上所述:当运动时间为
s或
s时,以C、P、Q为顶点的三角形恰与△ABC相似.
【解析】【分析】由题意可求出sin∠A=
,
然后根据正弦函数的概念以及BC的值可得AB的值,进而求得AC的值,然后表示出BP、CQ、PC,分①∠PQC=∠A;②∠PQC=∠B,结合相似三角形对应边成比例求解即可.
五、综合题
22.【答案】
(1)证明:
,
.
,
,
又
,
;
(2)解:
,
,
,
,
.
【解析】【分析】(1)先求出∠ADF=∠C,再证明三角形相似求解即可;
(2)根据相似三角形的性质计算求解即可。
23.【答案】
(1)证明:∵四边形ABCD是矩形
∴∠ABE=90°
∴∠ABG+∠EBG=90°
∵
∴∠ABG+∠BAG=90°
∴∠EBG=∠BAG
∴Rt△BEG∽Rt△AEB
∴
∴
(2)证明:由(1)有:
∵BE=CE
∴
∴
∵∠CEG=∠AEC
∴△CEG∽△AEC
∴∠CGE=∠ACE
∵四边形ABCD是矩形
∴AC=BD
∴OB=OC
∴∠DBC=∠ACE
∴
【解析】【分析】(1)先求出
∠EBG=∠BAG
,再求出
Rt△BEG∽Rt△AEB
,最后证明求解即可;
(2)先求出
∠CGE=∠ACE
,再求出
∠DBC=∠ACE
,最后证明求解即可。
五、解答题(三)(每小题10分,共20分)
24.【答案】
(1)证明:如图1,
由
折叠得到,
,
.
又
四边形ABCD是正方形,
,
,
,
又
正方形
,
(2)解:如图,连接
,
由(1)得
,
,
由折叠得
,
,
.
四边形
是正方形,
,
,
又
,
,
.
,
,
,
.
,
,
(
舍去)
(3)解:如图,连结HE,
由已知
可设
,
,可令
,
①当点H在D点左边时,如图,
同(2)可得,
,
,
由折叠得
,
,
又
,
,
,
又
,
,
,
,
,
,
.
,
,
,
(
舍去).
②当点
在
点右边时,如图,
同理得
,
,
同理可得
,
可得
,
,
,
,
(
舍去).
【解析】【分析】(1)利用折叠的性质可证得BE⊥CF,利用正方形的性质可得到BC=CD,∠D=∠BCE,利用余角的性质可得到∠BEC=∠CGD;然后利用AAS可证得结论.
(2)利用全等三角形的性质可求出DG的长,利用折叠的性质可得到BC=BF,CE=EF=9;再证明∠HFG=∠HGF,利用等角对等边可证得HF=HG,结合已知条件可求出HD,HF的长;再利用勾股定理建立关于DE的方程,解方程求出DE的长.
(3)连结HE,
设DH=4m,HG=5m,
,①当点H在D点左边时,同理可证得HF=HG,可得到DG=9,利用折叠的性质及余角的性质可推出∠BEC=∠CGD,利用有两组对应角相等的两三角形相似,可证得△CDG∽△BCE,利用相似三角形的性质,可表示出CE的长,即可得到DE的长;然后利用勾股定理,可求出x的值,即可得到DE与EC的比值;②当点
在
点右边时,如图,同理可证得△CDG∽△BCE,利用相似三角形的性质,可表示出CE的长,即可得到DE的长;然后利用勾股定理,可求出x的值,即可得到DE与EC的比值.
25.【答案】
(1)解:∵AB=24cm,BC=16cm,点E为边CD的中点,
∴CE=12cm,
在Rt△ECB中,根据勾股定理,得BE=
20(cm),
过P作PG⊥QB于G,
若点P在线段BQ的垂直平分线上,
则PQ=PB,GB=
BQ=
(24﹣3t),
∵∠C=∠PGB=90°,
∵CD∥AB,
∴∠PBG=∠BEC,
∴△PBG∽△BEC,
∴
,即
,
∴t=
,
∴当t=
时,点P在线段BQ的垂直平分线上;
(2)解:∵四边形ABCD是矩形,AB=24cm,BC=16cm,点E为边CD的中点,
∴DE=CE=12,∠C=∠D=90°,∠DEF+∠DFE=90°,
∵EF⊥BE,
∴∠DEF+∠CEB=90°,
∴∠DFE=∠CEB,
∴△DFE∽△CEB,
∴
,即
,
∴DF=9,
由(1)知,△PBG∽△BEC,
∴
,即
,
∴PG=
,
∴五边形AFEPQ的面积y=S矩形ABCD﹣S△BEC﹣S△DEF﹣S△PBQ
=24×16﹣
×12×16﹣
×12×9﹣
(24﹣3t)×
=
,
∴y与t的函数关系式为:y=
;
(3)解:∵S五边形AFEPQ∶S矩形ABCD=33∶64,
∴
=
×24×16,即t2﹣8t+15=0,
解得:t1=3,t2=5,
∴存在,t的值为3或5
(4)解:过Q作QM⊥EF于M,若点Q在∠AFE的平分线上,则QM=QA,分别延长EF、BA相交于点O,
∵四边形ABCD是矩形,
∴AB∥CD,
∴△OAF∽△EDF,
∴
,
∴OA=
,
∴OB=AB+OA=24+
=
,
∵QM⊥EF,EF⊥BE,
∴QM∥BE,
∴
,即
,
∴QM=
,
∴
,
解得:t=
.
答:存在,t的值是
.
【解析】【分析】(1)
在Rt△ECB中,根据勾股定理,得BE=20,过P作PG⊥QB于G,证明△PBG∽△BEC,根据相似三角形的性质求解即可;
(2)?证明△DFE∽△CEB,可得
,
据此求出DF,由(1)知△PBG∽△BEC,可得
,
据此求出PG,利用五边形AFEPQ的面积y=S矩形ABCD﹣S△BEC﹣S△DEF﹣S△PBQ,即可求出关系式;
(3)由S五边形AFEPQ∶S矩形ABCD=33∶64,建立方程,求出t值即可;
(4)过Q作QM⊥EF于M?,根据角平分线的性质得出QM=QA,
分别延长EF、BA相交于点O,?证明
△OAF∽△EDF,
利用相似三角形的性质求出OA,从而求出OB,由QM∥BE,可得
,
从而求出QM=??
,
?从而得出
,
解出t值即可.
?
(
第
一
页
共
1
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
广东省佛山市高明区2021-2022学年度北师大版九年级上册
第四章《图形的相似》检测卷
一、选择题(每小题3分,共30分)
1.下列四组线段中,不能成比例的是(??
)
A.?a=3,b=6,c=2,d=4???????
????????B.?a=1,b=3,c=2,d=6
C.?a=4,b=6,c=5,d=10????????????????????????????????D.?a=2,b=5,c=4,d=10
2.如果5x=6y,那么下列结论正确的是(?
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
3.如图,
ABC中,点D、E分别在AB、AC上,且
,下列结论正确的是(??
)
A.?DE:BC=1:2???????????????????????????????????????????????????B.?
ADE与
ABC的面积比为1:3
C.?
ADE与
ABC的周长比为1:2??????????????????D.?DE
BC
4.用一个10倍的放大镜去观察一个三角形,下列说法中正确的是(??
)
①三角形的每个角都扩大10倍;②三角形的每条边都扩大10倍;
③三角形的面积扩大10倍;④三角形的周长扩大10倍.
A.?①②??????????????????B.?①③??????????????????????C.?②④???????????
???D.?②③
5.如图,□ABCD中,EF∥AB,DE∶DA
=
2∶5,EF
=
4,则CD的长为(???
)
A.
B.8
C.10
D.16
6.如图,
和
是位似三角形,位似中心为点
,
,则
和
的位似比为(??
)
A.???????????????????????????????B.?????????????????????????????C.??????????????????????????????????D.?
7.如图,
、
交于
点,
,则下列结论一定正确的是(???
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
8.如图,△ABC是一张锐角三角形的纸片,AD是边BC上的高,已知BC=20cm,AD=15cm,从这张纸片上剪一下一个矩形,使矩形的一边在BC上,另两个顶点分别在AB、AC上。则下列结论不正确的是(
???)
A.?当△AHG的面积等于矩形面积时,HE的长为5cm
B.?当HE的长为6cm时,剪下的矩形的边HG是HE的2倍
C.?当矩形的边HG是HE的2倍时,矩形面积最大
D.?当矩形的面积最大时,HG的长是10cm
9.如图,在平行四边形
中,F是
上一点,且
,连结
并延长交
的延长线于点G
,
则
的值为(
??)
A.???????????????????????????????B.????????????????????????????????C.????????????????????????????D.?
10.如图,正方形
中,点
是
边上一点,连接
,以
为对角线作正方形
,边
与正方形
的对角线
相交于点
,连接
.以下四个结论:①
;②
;③
;④
.其中正确的个数为(??
)
A.?1个?????????????????????????B.?2个??????????????????????????C.?3个????????????????????????D.?4个
二、填空题(每小题4分,共28分)
11.已知
,则
=________.
12.在某一时刻,测得一根高为1.5
m的竹竿的影长为3
m,同时同地测得一栋楼的影长为60
m,则这栋楼的高度为________m.
13.在平面直角坐标系中,点
的坐标为
,点
的坐标为
,在第三象限内作与
位似的
,点
的对应点为点
,
与
的位似比为
,则点
的坐标为________.
14.如图,在四边形ABCD中,AD∥BC.BC=2AD,若S△AOD=1,则S△ABC=________.
15.两个等边三角形
和
,点D在BC上,AC与DE交于点F
,
BD=4,CD=2,则AF的长为________.
16.如图,在
中,
,
,点P是
边的中点,点Q是
边上一动点,若
与
相似,则
的长为________.
17.如图,在平行四边形
中,
为
的中点,
为
上点,
交
于点
,
,
,
,则
的长为________cm.
第14题图
第15题图
第16题图
第17题图
三、解答题(一)(每小题6分,共18分)
18.已知x:y=2:3,求:
(1)
的值;
(2)若x+y=15,求x,y的值.
19.已知:如图,△ABC∽△ACD,CD平分∠ACB,AD
=2,BD
=3,求AC、DC的长.
20.如图,利用标杆
测量楼高,点A,D,B在同一直线上,
,
,垂足分别为E,C.若测得
,
,
,楼高
是多少?
四、解答题(二)(每小题8分,共24分)
21.如图所示,∠C=90°,BC=8cm,cosA=3︰5,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
22.如图,在
中,点
、
分别在边
,
上,
,线段
分别交线段
,
于点
,
,且
.
(1)求证:
;
(2)若
,求
的值.
23.如图,已知矩形
的两条对角线相交于点O
,
过点
作
分别交
、
于点
、
.
(1)求证:
;
(2)连接
,若
.求证:
.
五、解答题(三)(每小题10分,共20分)
24.如图,
(1)【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G.
求证:
.
(2)【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若
,
,求线段DE的长.
(3)【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若
,
,求
的值(用含k的代数式表示).
25.已知:如图,在矩形ABCD中,AB=24cm,BC=16cm,点E为边CD的中点,连接BE
,
EF⊥BE交AD于点F
.
点P从点B出发,沿BE方向匀速运动,速度为2cm/s;同时,点Q从点A出发,沿AB方向匀速运动,速度为3cm/s.当一个点停止运动时,另一个点也停止运动.设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,点P在线段BQ的垂直平分线上?
(2)连接PQ
,
设五边形AFEPQ的面积为y(cm2),求y与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t
,
使S五边形AFEPQ∶S矩形ABCD=33∶64?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t
,
使点Q在∠AFE的平分线上?若存在,求出t的值;若不存在,请说明理由.
答案解析部分
一、选择题(每小题3分,共30分)
1.【答案】
C
【解析】【解答】解:A、∵2×6=3×4,∴四组线段中能成比例;不符合题意;
B、∵1×6=3×2,∴四组线段中能成比例;不符合题意;
C、∵4×10≠5×6,∴四组线段中不能成比例;符合题意;
D、∵2×10=4×10,∴四组线段中能成比例;不符合题意;
故答案为:C.
【分析】根据比例的性质验证四条线段是否两两乘积相等即可判断求解.
2.【答案】
A
【解析】【解答】A,
可以得出:
故答案为:A.
【分析】根据两内项之积等于两外项之积可判断求解.
3.【答案】
D
【解析】【解答】解:∵
,
∴AD:AB=AE:AC=1:3,
∵∠A=∠A,
∴△ADE∽△ABC,
∴DE:BC=1:3,故A错误;
∵△ADE∽△ABC,
∴△ADE与△ABC的面积比为1:9,周长的比为1:3,故B和C错误;
∵△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.故D正确.
故答案为:D.
【分析】由已知条件可得AD:AB=AE:AC=1:3,证明△ADE∽△ABC,由相似三角形的性质可判断A、B、C;由相似三角形对应角相等可得∠ADE=∠B,利用平行线的判定定理可判断D.
4.【答案】
C
【解析】【解答】解:①三角形的每个角不会变化,故错误;
②三角形的每条边都扩大10倍,故正确;
③三角形的面积会扩大100倍,故错误;
④三角形的周长会扩大10倍,故正确.
故答案为:C.
【分析】①由三角形的内角和等于180°可知,用一个10倍的放大镜去观察一个三角形,三角形的每个角不会变化;
②三角形的每条边都扩大10倍;
③根据S△=底×高可知,三角形的面积会扩大100倍;
④三角形的周长会扩大10倍.
5.【答案】
C
【解析】【解答】∵EF∥AB
∴△DEF∽△DAB
∴
∴AB=10
∴CD=AB=10
故答案为:C.
【分析】先证明△DEF∽△DAB,再求出
,
最后计算求解即可。
6.【答案】
D
【解析】【解答】解:∵
,
∴
,
∴
和
的位似比为
,
故答案为:D.
【分析】利用位似图形的性质即可求解.
7.【答案】
C
【解析】【解答】解:
,
,
,故A不符合题意,
,
,
,
,故B不符合题意,
,
,
,
,
,故C符合题意,
,
,
,
,故D不符合题意.
故答案为:C.
【分析】先求出△AEO△ABC,再根据
?和相似三角形的性质对每个选项一一判断即可。
8.【答案】
C
【解析】【解答】解:A.∵
△AHG的面积等于矩形面积,
∴HG·AP=HG·PD,
∴AP=PD,
∴(15-PD)=PD,
∴HE=PD=5(cm),
故A正确;
B.∵△AHG∽△ABC,
∴
,
∴
,
∴HG=12=2HE,
故B正确;
C.
∵△AHG∽△ABC,
∴
,
∴
,
解得:HG=20-HE,
∴S矩形=HG·HE=(20-HE)·HE=-HE2+20HE=-(HE-)2+75,
∴当HE=-时,
S矩形最大,
∴HG=20-HE=10(cm),
故C不正确,D正确.
故答案为:C.
【分析】A.根据三角形的面积和矩形的面积公式列出等式,得出(15-PD)=PD,求出PD的长,即可求出HE的长,从而判断A正确;
B.先证出△AEF∽△ABC,列出比例式,得出
,
求出HG的长,即可判断B正确;
CD.根据△AHG∽△ABC,得出
,
得出HG=20-HE,进而得出矩形EFHG的面积为-(HE-)2+75,利用二次函数的性质得出当HE=-时,
S矩形最大,再求出HG的长,即可判断C不正确,D正确.
9.【答案】
C
【解析】【解答】解:根据题意,
∵四边形
是平行四边形,
∴AB∥CD
,
∴△ABF∽△DGF
,
∴
,
∴
,
∴
,
∴
,
∵AB∥CD
,
∴△ABE∽△CGE,
∴
;
故答案为:C.
【分析】由四边形
是平行四边形,可证出△ABF∽△DGF
,
再利用平行线分线段成比例的了即可解决问题。
10.【答案】
D
【解析】【解答】解:①∵四边形AEFG和四边形ABCD均为正方形
∴∠EAG=∠BAD=90°
又∵∠EAB=90°-∠BAG,∠GAD=90°-∠BAG
∴∠EAB=∠GAD
∴①正确②∵四边形AEFG和四边形ABCD均为正方形
∴AD=DC,AG=FG
∴AC=
AD,AF=
AG
∴
,
即
又∵∠DAG+∠GAC=∠FAC+∠GAC
∴∠DAG=∠CAF
∴
∴②正确③∵四边形AEFG和四边形ABCD均为正方形,AF、AC为对角线
∴∠AFH=∠ACF=45°
又∵∠FAH=∠CAF
∴△HAF∽△FAC
∴
即
又∵AF=
AE
∴
∴③正确④由②知
又∵四边形ABCD为正方形,
AC为对角线
∴∠ADG=∠ACF=45°
∴DG在正方形另外一条对角线上
∴DG⊥AC
∴④正确
故答案为:D.
【分析】根据正方形的性质可得∠EAG=∠BAD=90°,利用同角的余角相等可得∠EAB=∠GAD,据此判断①;根据两组对边成比例且夹角相等,可证
,
据此判断②;先证△HAF∽△FAC,可得
,
可得
,
由AF=
AE,即得
,
据此判断③;由
,
可得∠ADG=∠ACF=45°,从而求出∠AND=90°,据此判断④.
二、填空题(每小题4分,共28分)
11.【答案】
【解析】【解答】解:∵
∴
设
=k,则a=2k,b=5k
∴
.
故填
.
【分析】
12.【答案】
30
【解析】【解答】解:设这栋楼的高度为hm,
∵在某一时刻,测得一根高为1.5m的竹竿的影长为3m,同时测得一栋楼的影长为60m,
∴
=
,
解得h=30.
故答案为:30.
【分析】先求出
=
,再解方程即可。
13.【答案】
【解析】【解答】解:∵
与
位似,点
的对应点为点
,
与
的位似比为
,
∵点
的坐标为
,点
在第三象限内,
∴点
的横纵坐标分别为:
,
;
∴点
的坐标为
;
故答案为:
;
【分析】根据相似和点C所在的象限求解即可。
14.【答案】
6
【解析】【解答】解:∵四边形ABCD中,AD//BC.
∴△AOD∽△COB.
∵AD
=
2BC.
∴AD:BC=1:2,
∴OD:OB=AD:BC=1:2,S△BOC=4
S△AOD=4
∴S△AOD:S△AOB
=1:2,即S△AOB
=2
∴S△ABC=S△BOC+
S△AOB
=4+2=6.
故填6.
【分析】
15.【答案】
【解析】【解答】∵
和
都是等边三角形,BD=4,CD=2,
∴AB=AC=BC=6,∠B=∠C=∠ADF=60°,
∴∠ADB+∠BAD=∠ADB+∠CDF=120°,
∴∠BAD=∠CDF,
∴
,
∴
,即
,
解得
,
∴
,
故答案为:
.
【分析】先求出∠BAD=∠CDF,再求出
,
最后计算求解即可。
16.【答案】
5或
【解析】【解答】∵
,
,点P是
边的中点
∴
当
时
∴
即
解得:
∴
当
时
∴
即
解得:
∴
∴
或
故答案为:
或
.
【分析】利用
或者
,分别得出答案。
17.【答案】
7.5
【解析】【解答】过点E作
,交AC于点H,如下图:
∵
∴
又∵
∴
∴
又∵四边形
是平行四边形,
且
为
的中点,
∴
,
,
∵
,
∴
,
∴
,
∴
cm.
故答案为:7.5
【分析】过点E做EH//AD,构造相似三角形,由相似性质得对应线段成比例,因为
且
为
的中点,由中位线推论得:EH是△ABC的中位线,因此。已知AF=1,DF=2,所以,因此,综合看,因此,
,
所以
,
AC=2AH=
三、解答题(一)(每小题6分,共18分)
18.【答案】
(1)解:
=
=﹣2
(2)解:∵x+y=15,
∴2k+3k=15,
解得:k=3,
∴x=6,y=9
【解析】【分析】(1)由已知的比例式可设x=2k,y=3k;(1)把x、y的值代入代数式计算即可求解;
(2)把x、y的值代入等式x+y=15可得关于k的方程,解方程可求得k的值,则x、y的值可求解.
?
?
19.【答案】
证明:
如图
∵△ABC∽△ACD,
∴∠1=∠B,
又∵CD是平分∠ACB,
∴∠1=∠2,
∴∠2=∠B,
∴BD=DC.
∵BD=3,
∴DC=3;
又∵AD
=2,BD
=3,
∴AB=5
由
得
即
=2×5=10
∴
.
【解析】【分析】利用相似三角形的性质得到
∠1=∠B,?
,把已知数据代入比例式求解即可得到AC的长;再结合角平分线的性质、等腰三角形的判定可求出DC的长。
20.【答案】
解:∵
,
,
∴
m,
∵
,
,
∴
∥
,
∴△ADE∽△ABC,
∴
,
∵
,
∴
,
∴
;
∴楼高
是9米.
【解析】【分析】由??,?
,
可得?∥?
,
可证△ADE∽△ABC,可得
,
代入相应数据,即可求出BC.
四、解答题(二)(每小题8分,共24分)
21.【答案】
解:∵∠C=90°,cosA=3︰5,
∴
,
∵BC=8cm,
∴
,
,
∵点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,设运动时间为t秒,则有:
,
∴
,
①当
时,则
,
∴
,即
,
解得:
,
②当
时,则
,
∴
,即
,
解得:
;
综上所述:当运动时间为
s或
s时,以C、P、Q为顶点的三角形恰与△ABC相似.
【解析】【分析】由题意可求出sin∠A=
,
然后根据正弦函数的概念以及BC的值可得AB的值,进而求得AC的值,然后表示出BP、CQ、PC,分①∠PQC=∠A;②∠PQC=∠B,结合相似三角形对应边成比例求解即可.
五、综合题
22.【答案】
(1)证明:
,
.
,
,
又
,
;
(2)解:
,
,
,
,
.
【解析】【分析】(1)先求出∠ADF=∠C,再证明三角形相似求解即可;
(2)根据相似三角形的性质计算求解即可。
23.【答案】
(1)证明:∵四边形ABCD是矩形
∴∠ABE=90°
∴∠ABG+∠EBG=90°
∵
∴∠ABG+∠BAG=90°
∴∠EBG=∠BAG
∴Rt△BEG∽Rt△AEB
∴
∴
(2)证明:由(1)有:
∵BE=CE
∴
∴
∵∠CEG=∠AEC
∴△CEG∽△AEC
∴∠CGE=∠ACE
∵四边形ABCD是矩形
∴AC=BD
∴OB=OC
∴∠DBC=∠ACE
∴
【解析】【分析】(1)先求出
∠EBG=∠BAG
,再求出
Rt△BEG∽Rt△AEB
,最后证明求解即可;
(2)先求出
∠CGE=∠ACE
,再求出
∠DBC=∠ACE
,最后证明求解即可。
五、解答题(三)(每小题10分,共20分)
24.【答案】
(1)证明:如图1,
由
折叠得到,
,
.
又
四边形ABCD是正方形,
,
,
,
又
正方形
,
(2)解:如图,连接
,
由(1)得
,
,
由折叠得
,
,
.
四边形
是正方形,
,
,
又
,
,
.
,
,
,
.
,
,
(
舍去)
(3)解:如图,连结HE,
由已知
可设
,
,可令
,
①当点H在D点左边时,如图,
同(2)可得,
,
,
由折叠得
,
,
又
,
,
,
又
,
,
,
,
,
,
.
,
,
,
(
舍去).
②当点
在
点右边时,如图,
同理得
,
,
同理可得
,
可得
,
,
,
,
(
舍去).
【解析】【分析】(1)利用折叠的性质可证得BE⊥CF,利用正方形的性质可得到BC=CD,∠D=∠BCE,利用余角的性质可得到∠BEC=∠CGD;然后利用AAS可证得结论.
(2)利用全等三角形的性质可求出DG的长,利用折叠的性质可得到BC=BF,CE=EF=9;再证明∠HFG=∠HGF,利用等角对等边可证得HF=HG,结合已知条件可求出HD,HF的长;再利用勾股定理建立关于DE的方程,解方程求出DE的长.
(3)连结HE,
设DH=4m,HG=5m,
,①当点H在D点左边时,同理可证得HF=HG,可得到DG=9,利用折叠的性质及余角的性质可推出∠BEC=∠CGD,利用有两组对应角相等的两三角形相似,可证得△CDG∽△BCE,利用相似三角形的性质,可表示出CE的长,即可得到DE的长;然后利用勾股定理,可求出x的值,即可得到DE与EC的比值;②当点
在
点右边时,如图,同理可证得△CDG∽△BCE,利用相似三角形的性质,可表示出CE的长,即可得到DE的长;然后利用勾股定理,可求出x的值,即可得到DE与EC的比值.
25.【答案】
(1)解:∵AB=24cm,BC=16cm,点E为边CD的中点,
∴CE=12cm,
在Rt△ECB中,根据勾股定理,得BE=
20(cm),
过P作PG⊥QB于G,
若点P在线段BQ的垂直平分线上,
则PQ=PB,GB=
BQ=
(24﹣3t),
∵∠C=∠PGB=90°,
∵CD∥AB,
∴∠PBG=∠BEC,
∴△PBG∽△BEC,
∴
,即
,
∴t=
,
∴当t=
时,点P在线段BQ的垂直平分线上;
(2)解:∵四边形ABCD是矩形,AB=24cm,BC=16cm,点E为边CD的中点,
∴DE=CE=12,∠C=∠D=90°,∠DEF+∠DFE=90°,
∵EF⊥BE,
∴∠DEF+∠CEB=90°,
∴∠DFE=∠CEB,
∴△DFE∽△CEB,
∴
,即
,
∴DF=9,
由(1)知,△PBG∽△BEC,
∴
,即
,
∴PG=
,
∴五边形AFEPQ的面积y=S矩形ABCD﹣S△BEC﹣S△DEF﹣S△PBQ
=24×16﹣
×12×16﹣
×12×9﹣
(24﹣3t)×
=
,
∴y与t的函数关系式为:y=
;
(3)解:∵S五边形AFEPQ∶S矩形ABCD=33∶64,
∴
=
×24×16,即t2﹣8t+15=0,
解得:t1=3,t2=5,
∴存在,t的值为3或5
(4)解:过Q作QM⊥EF于M,若点Q在∠AFE的平分线上,则QM=QA,分别延长EF、BA相交于点O,
∵四边形ABCD是矩形,
∴AB∥CD,
∴△OAF∽△EDF,
∴
,
∴OA=
,
∴OB=AB+OA=24+
=
,
∵QM⊥EF,EF⊥BE,
∴QM∥BE,
∴
,即
,
∴QM=
,
∴
,
解得:t=
.
答:存在,t的值是
.
【解析】【分析】(1)
在Rt△ECB中,根据勾股定理,得BE=20,过P作PG⊥QB于G,证明△PBG∽△BEC,根据相似三角形的性质求解即可;
(2)?证明△DFE∽△CEB,可得
,
据此求出DF,由(1)知△PBG∽△BEC,可得
,
据此求出PG,利用五边形AFEPQ的面积y=S矩形ABCD﹣S△BEC﹣S△DEF﹣S△PBQ,即可求出关系式;
(3)由S五边形AFEPQ∶S矩形ABCD=33∶64,建立方程,求出t值即可;
(4)过Q作QM⊥EF于M?,根据角平分线的性质得出QM=QA,
分别延长EF、BA相交于点O,?证明
△OAF∽△EDF,
利用相似三角形的性质求出OA,从而求出OB,由QM∥BE,可得
,
从而求出QM=??
,
?从而得出
,
解出t值即可.
?
(
第
一
页
共
1
页
)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
