11.5机械效率 同步练习 2021-2022学年苏科版九年级物理 上册(含答案)
文档属性
| 名称 | 11.5机械效率 同步练习 2021-2022学年苏科版九年级物理 上册(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 373.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-23 06:01:29 | ||
图片预览




文档简介
11.5
机械效率
一.选择题(共12小题)
1.下列关于功率、机械效率说法中,正确的是( )
A.机械效率越高,机械做功一定越快
B.做功越多的机械,机械效率越高
C.做功越快的机械,功率越大
D.功率越大的机械,做功一定越多
2.用如图重为G的均匀杠杆,先后把同一重物挂在A、B两处匀速提升相同高度,支点处的摩擦不计,下列说法正确的是( )
A.重物在A点处人做的有用功多
B.在提升重物时杠杆可节省距离
C.重物在A点处杠杆的机械效率更高
D.重物在B点处杠杆的机械效率更高
3.甲乙两个滑轮组如图所示,其中每一个滑轮的重量都相同,用它们在相同时间内分别将重物G1、G2提高相同的高度,不计绳重和摩擦,下列说法正确的是( )
A.若G1=G2,则拉力做的总功相同
B.若G1=G2,则甲机械效率大于乙机械效率
C.若F1=F2,则拉力做功的功率相同
D.用甲、乙中的任何一个滑轮组提起不同的重物,机械效率不变
4.如图所示,重800N的物体在100N水平拉力F的作用下,以0.1m/s的速度沿水平地面向左匀速直线运动了20s,滑轮组的机械效率为60%。在此过程中,下列说法正确的是( )
A.拉力F做的功为400J
B.物体与地面间的滑动摩擦力为180N
C.额外功的功率为6W
D.若物体的重力和运动速度不变,只增大水平地面的粗糙程度,则滑轮组的机械效率会降低
5.小明用如图所示的装置研究“杠杆的机械效率时,将重为G的钩码挂在铁质杠杆上A点,弹簧测力计作用于C点,竖直向上匀速拉动弹簧测力计,使钩码上升h高度,杠杆的机械效率为η1;在小明的装置基础上,小红仅改为将弹簧测力计作用于B点,竖直向上匀速拉动弹簧测力计,仍使钩码上升h高度,杠杆的机械效率为η2:在小明的装置基础上,小华仅改为将钩码挂到B点,竖直向上匀速拉动弹簧测力计,仍使钩码上升h高度,杠杆的机械效率为η3;则( )
A.η1<η2,η1<η3
B.η1=η2,η1<η3
C.η1=η2,η1=η3
D.η1>η2,η1>η3
6.如图所示,斜面长3m,高0.6m,小明用绳子在6s内将重50N的物体从其底端沿斜面向上匀速拉到顶端,拉力F是15N。下列说法中正确的是( )
A.斜面上的摩擦力是5N
B.拉力所做的功是30J
C.拉力做功的功率是5W
D.斜面的机械效率是80%
7.小明用动滑轮竖直向上提升重物,下列措施能提高动滑轮机械效率的是( )
A.减小动滑轮的重力
B.增大重物上升的高度
C.减小物体的重力
D.增大重物上升的速度
8.如图所示,在探究“斜面的机械效率”实验中,一下说法错误的是( )
A.木块沿斜面匀速上升的过程中,拉力和摩擦力是一对平衡力
B.用弹簧测力计沿着斜面向上拉木块时,应尽量匀速
C.斜面的倾斜程度影响斜面的机械效率
D.斜面的倾斜程度越小,所需的拉力越小
9.小明用如图所示的装置探究杠杆的机械效率,他将两个钩码悬挂在B点,在A点用弹簧测力计保持竖直方向拉动杠杆,使其绕O点缓慢转动,带动钩码上升一定的高度h(不计摩擦)( )
A.在杠杆转动过程中,弹簧测力计的示数会变小
B.仅将拉力的作用点从A点移到C点,杠杆的机械效率不变
C.仅增加钩码的个数,拉力所做的额外功增大
D.仅将钩码的悬挂点从B点移到C点,拉力做的总功变大
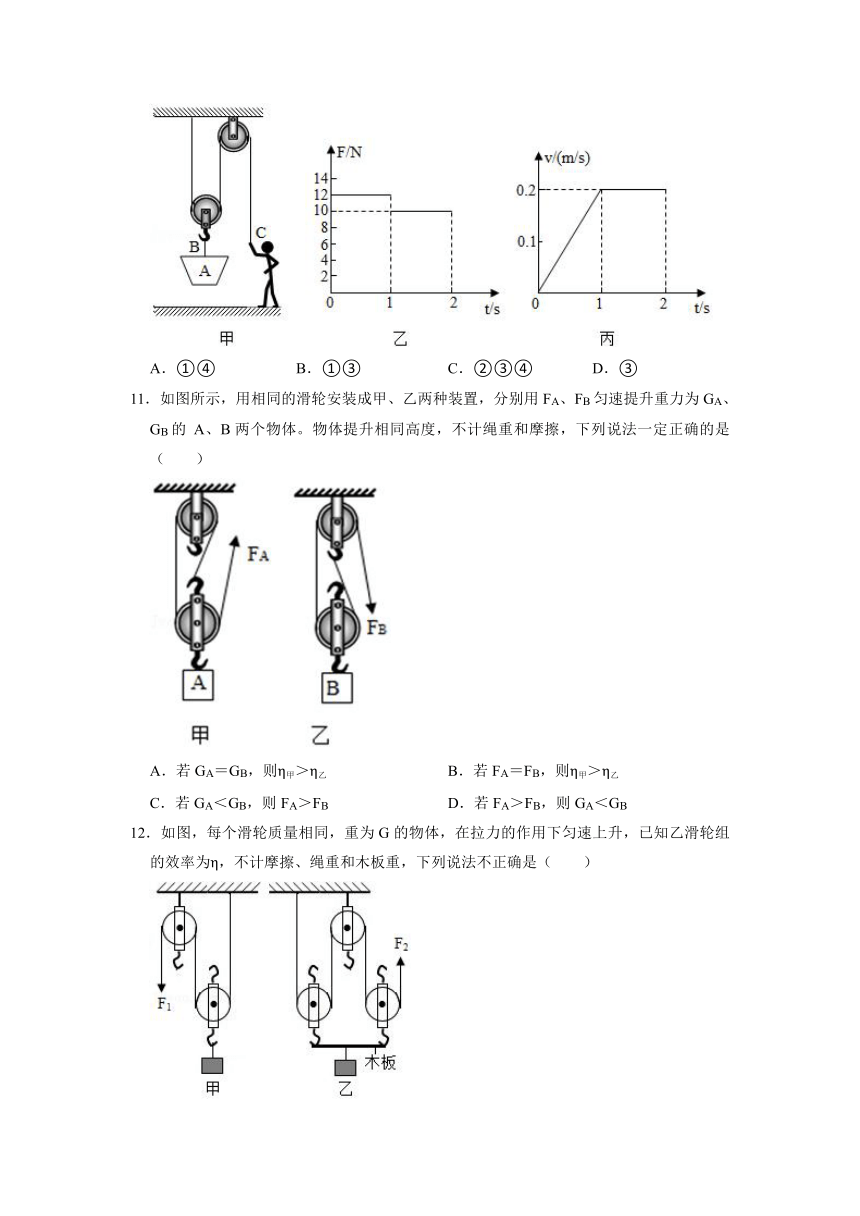
10.如图甲所示的装置,A是重10N的空吊篮,绳子B和C能承受的最大拉力分别为100N和60N。质量为50kg的小张同学将A提升到高处,施加的拉力F随时间变化关系如图乙所示,A上升的速度v随时间变化关系如图丙所示。忽略绳重及摩擦,(g=10N/kg)。下列结论正确的是( )
①动滑轮的重力为9N;
②0~1s内拉力F做的功为2.4J;
③1~2s内拉力F的功率为4W;
④此装置提升重物的最大机械效率约为81.8%。
A.①④
B.①③
C.②③④
D.③
11.如图所示,用相同的滑轮安装成甲、乙两种装置,分别用FA、FB匀速提升重力为GA、GB的
A、B两个物体。物体提升相同高度,不计绳重和摩擦,下列说法一定正确的是( )
A.若GA=GB,则η甲>η乙
B.若FA=FB,则η甲>η乙
C.若GA<GB,则FA>FB
D.若FA>FB,则GA<GB
12.如图,每个滑轮质量相同,重为G的物体,在拉力的作用下匀速上升,已知乙滑轮组的效率为η,不计摩擦、绳重和木板重,下列说法不正确是( )
A.两滑轮组的机械效率可能相等
B.F1一定大于F2
C.每个滑轮重
D.甲、乙将重物提升相同的高度时,拉力的功率可能相等
二.填空题(共6小题)
13.在实际生产劳动中使用机械时,总要做一些额外功,原因是任何机械本身都有
,并且机械零件与零件之间在发生相对运动时还存在着
,所以任何机械的机械效率总
100%(选填“大于”或“小于”)。
14.如图所示甲、乙两装置中所用滑轮相同,现分别用拉力F1、F2匀速提升重为G1、G2的两物体,不计绳重和摩擦。
(1)若F1=5N,G1=9N,则甲装置的机械效率是:
。
(2)若F1=F2,则甲装置的机械效率η甲
乙装置的机械效率η乙。(选填“大于”、“小于”或“等于”)
15.小明不小心将水桶掉入井中,用钩子将质量为1kg的桶从离井口5m的深处匀速捞到井口,称出桶内水的质量为9kg,这次捞桶的过程中,做的有用功是
J,额外功是
J,总功是
J,机械效率为
(g取10N/kg)。
16.如图所示,物体重180N,小明用100N的拉力(方向不变)将物体匀速提升2m,用了10s,则此过程中有用功
J,拉力的功率
W,滑轮组的机械效率
。
17.如图所示,弹簧测力计的示数为
N,钩码的重力为1.0N,钩码上升的高度h为0.1m,测力计竖直向上移动的距离s为0.3m,此时杠杆的机械效率为
。忽略杠杆转动轴的摩擦,仅将钩码的悬挂点从A移到B,若重物提升高度相同,则额外功与有用功的比值将
(增大/减小/不变),杠杆的机械效率将
。(增大/减小/不变)
18.如图,小明将一个重为3N的小车从斜面底端匀速拉到斜面顶端,沿斜面向上的拉力为1.25N,小车沿斜面移动的距离s=1.6m,上升的高度h=0.6m。则小明对小车做的有用功是
J,斜面的机械效率是
。
三.实验探究题(共2小题)
19.如图所示,“测滑轮组机械效率”的实验,实验得到的数据如表。
钩码重G/N
钩码上升高度h/m
绳端拉力F/N
绳端移动距离S/m
机械效率η
l
4
0.1
1.8
0.3
74%
2
4
0.1
1.4
0.5
57%
3
6
0.1
2.4
0.3
83%
(1)实验中应沿
拉动弹簧测力计,使钩码上升;
(2)从表中数据可分析出第1次是用
图的装置进行的实验;
(3)通过分析1,2次实验数据,可得结论:使用不同的滑轮组提升相同的重物时,动滑轮越重,滑轮组的机械效率越
(填“高”“低”);
(4)在第1次实验基础上,做了第3次实验,通过对比分析第1和第3次两次实验数据,可得结论:使用同一滑轮组,
可以提高滑轮组的机械效率。
20.为探究斜面的机械效率与斜面倾斜程度之间的关系,某探究小组的同学利用木块、木板、刻度尺、弹簧测力计等器材设计了如图所示的实验装置。实验测得的数据如下表:
实验次数
侧面倾斜程度
木块重力G/N
斜面高度h/m
沿斜面拉力F/N
斜面长度s/m
机械效率η
1
较缓
3
0.2
1.6
1
37.5%
2
较陡
3
0.3
1.8
1
3
最陡
3
0.4
2.0
1
60.0%
请你根据表中的数据解答下列问题:
(1)实验中要求用沿斜面向上的力拉着木块在斜面上做
运动,若木块沿斜面加速运动,则测得的机械效率
(选填“偏大”、“偏小”或“不变”)。
(2)第2次实验中,斜面的机械效率为
。
(3)当斜面长度一定时,斜面的机械效率η与斜面的高度h之间的关系大概如图
所示。
(4)从表格中我们还可以看出斜面的倾斜程度越
(选填“缓”或“陡”)越省力。
四.计算题(共2小题)
21.如图所示,工人用滑轮组在20s内匀速提起一个150N的物体,物体上升了10m,拉力F为100N,不计绳重与摩擦,求:
(1)工人做的有用功;
(2)动滑轮的重力;
(3)滑轮组的机械效率.
22.在九年级物理拓展课上,李博同学模拟某建筑工地上塔吊的工作情景,设置了如图所示的滑轮组来提升装修材料,若他用250N的拉力将500N的材料以0.5m/s匀速提升了20s,(不计绳重和摩擦,g=10N/kg)。求:
(1)20s内拉力所做的功;
(2)提升500N材料时,此滑轮组的机械效率是多少;
(3)若绳子能承受的最大拉力为500N时,设该最大拉力小于人的重力,此滑轮组的机械效率最大可提高到多少。
一.选择题(共12小题)
1.【解答】解:A、机械效率和功率两者没有因果关系,如滑轮组的机械效率可到80%,起重机的效率只有40%左右,但是起重机的功率却比滑轮组大的多。所以,机械效率高,功率不一定大,做功不一定快。故A错误;
B、根据W=Pt可知,做功的多少与时间和功率有关,只要时间长功率大,做功就多,与机械效率无关。故B错误;
C、做功快的机械,说明单位时间内完成的功多,所以功率一定大。故C正确;
D、根据W=Pt可知,做功的多少与时间和功率有关,若只是功率大,但时间短做功也不一定多。故D错误。
故选:C。
2.【解答】解:
A、利用杠杆提升重物时,所做的有用功为W有用=Gh,在A、B两处提升的是同一个重物,上升同样的高度,所以在A、B两处人做的有用功相同,故A错误;
B、根据力臂的定义,由图可知,动力臂大于阻力臂,则该杠杆为省力杠杆,费距离,故B错误;
CD、由图可知,在A、B两处提升重物,重物上升同样的高度时,杠杆的重心上升的高度hA>hB,
由W额外=G杆h可知,W额外A>W额外B,
在A、B两处人做的有用功相同,而W总=W有用+W额外,所以W总A>W总B,
由η=可知ηA<ηB.故C错误,D正确。
故选:D。
3.【解答】解:A、甲滑轮组中有一个动滑轮,乙滑轮组中有两个动滑轮,所以若把物体提升相同的高度,乙滑轮组做的额外功多,若G1=G2,把物体提升相同的高度,则根据W=Gh可知甲乙所做的有用功相同,总功=有用功+额外功,有用功一样,乙图额外功功大,所以乙的总功大于甲的总功,故A错误;
B、若G1=G2,甲乙所做的有用功相同,乙做的总功大于甲做的总功,根据η=,甲的机械效率大于乙的机械效率,故B正确;
C、若F1=F2,由于甲图有2段绳子承担物重,所以s=2h,乙图有3段绳子承担物重,所以s=3h,根据P==在相同时间内,甲的功率小于乙的功率,故C错误;
D、用同一个滑轮组提起不同的重物,所做的额外功不变,有用功发生变化,所以有用功在总功中的比值发生变化,所以机械效率变,故D错误。
故选:B。
4.【解答】解:A、由图知,n=3,则绳子自由端移动的距离:s=3s物=3v物t=3×0.1m/s×20s=6m,拉力做功为:W总=Fs绳=100N×6m=600J,故A错误;
B、因为η====,所以物体与地面间的滑动摩擦力:f=ηnF=60%×3×100N=180N,故B正确;
C、因为η=,所以有用功:W有=ηW总=60%×600J=360J,
额外功:W额=W总﹣W有=600J﹣360J=240J,
额外功做功的功率:P===12W,故C错误;
D、如果只增大接触面的粗糙程度,增大了摩擦力,增大了有用功,而额外功几乎不变,有用功与总功的比值变大,机械效率变大,故D错误。
故选:B。
5.【解答】解:
(1)原来弹簧测力计作用于C点,竖直向上匀速拉动弹簧测力计时,测得杠杆的机械效率η1;将弹簧测力计移动到B点时,仍将钩码竖直向上匀速提升相同的高度,根据W有用=Gh可知有用功不变;
因杠杆的偏转角度不变,则杠杆重心上升的高度不变,根据W额=G杠杆h杠杆可知,克服杠杆重和摩擦所做额外功不变;由于有用功和额外功都不变,所以总功也不变,根据η=×100%可知杠杆的机械效率不变,即η2=η1;
;
(2)根据图示可知,将钩码移动到B点时,阻力和动力臂都不变,阻力臂增大,由F1L1=F2L2可知,动力将增大,即F′>F;将钩码移至B点,提升相同高度,有用功相同,弹簧测力计竖直移动的距离不同,B点时杠杆上上升的高度小些,做的额外功小些,所以机械效率变大,即η1<η3。
故选:B。
6.【解答】解:(1)此过程所做有用功为:W有=Gh=50N×0.6m=30J;
拉力所做总功为:W总=Fs=15N×3m=45J;
故机械效率为:η===66.7%;
(2)拉力做功的功率为:P===7.5W;
(3)此过程所做额外功为:W额=W总﹣W有=45J﹣30J=15J;
由W额=fs变形得:
摩擦力为:f===5N。
故BCD错误,A正确。
故选:A。
7.【解答】解:
A、减小动滑轮的重力,在其他条件不变时,需要做的额外功减少,有用功不变,能提高动滑轮的机械效率,故A符合题意;
BD、动滑轮的机械效率η====,说明机械效率的高低与物体被提升的高度及上升速度无关,故BD不符合题意;
C、减小重物的重力,在其他条件不变时,所做的有用功会减少,额外功不变,这样有用功在总功中所占的比例就会降低,即动滑轮的机械效率降低,故C不符合题意。
故选:A。
8.【解答】解:A、木块在上升过程中受到重力、支持力、拉力和摩擦力四个力的作用,由于重力使物体有下滑的趋势,所以,要使物体匀速上升,拉力应大于摩擦力,拉力和摩擦力不是一对平衡力,故A错误;
B、为了保证弹簧测力计的示数稳定,需使木块受到的力为平衡力,则要让木块做匀速直线运动,故B正确;
C、其他条件一定时,斜面倾斜程度越大,机械效率越高,故C正确;
D、斜面的倾斜程度越小,越省力,沿斜面所用的拉力越小,故D正确。
故选:A。
9.【解答】解:A、若弹簧测力计拉力方向一直竖直向上拉动,阻力不变,动力臂减小,阻力臂变小,如下图所示:
△OBB′∽△OAA′,所以=,所以动力臂与阻力臂的比值不变,
因为阻力不变,根据杠杆的平衡条件知,弹簧测力计的示数应该不变,故A错误;
B、仅将拉力的作用点从A点移到C点,由于将相同的钩码提升相同的高度,有用功不变,额外功也不变,杠杆的机械效率不变,故B正确;
C、克服杠杆重力做的功为额外功,仅增加钩码的个数,杠杆重力和杠杆上升的高度不变,拉力所做的额外功不变,故C错误;
D、钩码的悬挂点在B点时,由杠杆的平衡条件得F1?OA=G?OB;悬挂点移至C点时,由杠杆的平衡条件得F2?OA=G?OC;从图中可以看出,由OB到OC力臂变大,所以弹簧测力计的示数变大,有用功不变,但杠杆提升的高度减小,额外功减小,又因为总功等于额外功与有用功之和,因此此次弹簧测力计做的功将小于第一次做的功,即仅将钩码的悬挂点从B点移到C点,拉力做的总功变小,故D错误。
故选:B。
10.【解答】解:
①由图丙可知,在1~2s内,A被匀速提升,由图乙可知拉力F=10N,
由图知,n=2,忽略绳重及摩擦,拉力F=(GA+G动),则动滑轮重力:G动=2F﹣GA=2×10N﹣10N=10N,故①错误;
②由图丙可知,0~1s内物体上升的距离:h=×0.2m/s×1s=0.1m,
则自由端移动的距离:s=2h=2×0.1m=0.2m,
由图乙可知,0~1s内拉力F=12N,
则0~1s内拉力F做的功:W=Fs=12N×0.2m=2.4J,故②正确;
③由图丙可知,A上升的速度vA=0.2m/s,拉力端移动速度v=2vA=2×0.2m/s=0.4m/s,
1~2s内拉力F的功率:P=Fv=10N×0.4m/s=4W,故③正确;
④忽略绳重及摩擦,C处绳子拉力FC=(FB+G动)=(FB+10N),
则当C处最大拉力为60N时,B处拉力为110N;
当B处最大拉力为100N时,C处拉力为55N;所以要以B处最大拉力为准,B处的拉力:FB=GA+G货物=100N,
此装置最多能匀速运载货物的重力:G货物=FB﹣GA=100N﹣10N=90N;
此装置提升重物的机械效率随提升物重的增大而增大,此装置提升重物的最大机械效率:
η=====×100%≈81.8%,故④正确。
故选:C。
11.【解答】解:
由图可知,甲滑轮组承重的绳子股数n甲=3,乙滑轮组承重的绳子股数n乙=2,
A、不计绳重和摩擦,克服物体重力做的功为有用功,克服物体重力和动滑轮重力做的功为总功,
则滑轮组的机械效率:η=×100%=×100%=×100%;
若GA=GB,由题知动滑轮重力相同,则η甲=η乙,故A错误;
B、由图可知,n甲=3,n乙=2,
由F=(G+G动)可得,提升物体的重力:G=nF﹣G动,
则两物体的重力分别为:GA=3FA﹣G动,GB=2FB﹣G动,
若FA=FB,由上式可知GA>GB,
根据η=×100%可知,则η甲>η乙,故B正确;
C、甲滑轮组绳子自由端的拉力F甲=(GA+G动),
乙滑轮组绳子自由端的拉力F乙=(GB+G动),
若GA<GB,则FA<FB,故C错误;
D、由B项解答可知,两物体的重力分别为:GA=3FA﹣G动,GB=2FB﹣G动,若FA>FB,由上式可知,无法判断GA与GB的大小关系,故D错误。
故选:B。
12.【解答】解:
(1)由图可知,甲滑轮组只有1个动滑轮,乙滑轮组有2个动滑轮,且不计摩擦、绳和木板的重,
因克服物体重力G做的功为有用功,克服物重和动滑轮重做的功为总功,
所以,两滑轮组的机械效率分别为:η甲==,η乙==,则η甲>η乙,故A错误;
由η乙=可得,动滑轮的重力(即每个滑轮重):
G动=,故C正确;
(2)由图可知,n甲=2,n乙=4,不计摩擦、绳和木板的重,
则两滑轮组绳子的拉力分别为:
F1=(G+G动)=(2G+2G动),F2=(G+2G动),
因(2G+2G动)>(G+2G动),
所以,F1>F2,故B正确;
甲、乙将重物提升相同的高度,拉力做功为总功,则F1与F2的功率分别为:
P甲==,P乙==,
因t甲和t乙的关系不确定,所以,F1与F2的功率可能相等,故D正确。
故选:A。
二.填空题(共6小题)
13.【解答】解:机械做功就要做额外功,额外功主要包括机械自身的重力和零件的摩擦,机械效率总小于1。
故答案为:重力、摩擦、小于。
14.【解答】解:
(1)由滑轮组的结构知道承担物重的绳子股数n甲=3,不计绳重和摩擦,甲装置的机械效率:
η=×100%=×100%=×100%=×100%=×100%=60%
(2)由图可知,乙图承担物重的绳子股数n乙=2,若F1=F2,由题知两装置中动滑轮重相同,不计绳重及摩擦,由拉力F=(G+G动),可知,G1>G2,
由η=×100%=×100%=×100%可知甲装置的机械效率η甲大于乙装置的机械效率η乙。
故答案为:60%;大于。
15.【解答】解:有用功为:W有=Gh=mgh=1kg×10N/kg×5m=50J;
该过程中是为了打捞水桶,对水桶中的水所做的功为额外功,额外功为:W额外=G水h=m水gh=9kg×10N/kg×5m=450J
总功为:W总=W有+W额外=50J+450J=500J
机械效率为:η===10%。
故答案为:50;450;500;10%。
16.【解答】解:(1)有用功:W有=Gh=180N×2m=360J;
(2)由图可知n=2,绳子自由端移动的距离s=nh=2×2m=4m,
拉力做的总功:W总=Fs=100N×4m=400J,
则拉力做功的功率:P===40W;
(3)滑轮组的机械效率:η=×100%=×100%=90%。
故答案为:360;40;90%。
17.【解答】解:
(1)由图可知,弹簧测力计的分度值是0.1N,所以它的示数是0.5N。
(2)在实验过程中,有用功是:W有=Gh=1.0N×0.1m=0.1J,
总功是:W总=Fs=0.5N×0.3m=0.15J,
所以杠杆的机械效率:η=×100%=×100%≈66.7%;
(3)杠杆提升钩码时,对钩码做有用功,克服杠杆重做额外功,并且W有+W额=W总;
设杠杆重心升高的距离为h,所以,Gh1+G杠h=Fh2,G不变,h1不变,G杠不变,
钩码从A点到B点,钩码还升高相同的高度,有用功不变;
杠杆上旋的角度减小,杠杆升高的距离h变小,克服杠杆重力所做的额外功变小,所以额外功与有用功的比值将减小;
因为Gh1+G杠h变小,所以Fh2也变小;根据η==可知,总功变小,有用功不变,所以η增大。
故答案为:0.5;
66.7%;减小;增大。
18.【解答】解:(1)小明对小车做的有用功:
W有=Gh=3N×0.6m=1.8J;
(2)拉力做的总功:
W总=Fs=1.25N×1.6m=2J,
斜面的机械效率为:
η==×100%=90%。
故答案为:1.8;90%。
三.实验探究题(共2小题)
19.【解答】解:
(1)实验中应该匀速竖直向上拉动弹簧测力计,以保证拉力大小恒定;
(2)实验1中,s1=0.3m,h1=0.1m,所以n1===3,所以实验1是用甲图做的实验;
(3)由表中第1次实验和第2次实验的数据可知,使用不同的滑轮组提升相同的重物时,动滑轮的个数越多(动滑轮的质量越大),滑轮组的机械效率越低;
(4)比较实验数据1和3可知,使用同一滑轮组,其他条件相同时,增大提升的物重,可以提高滑轮组的机械效率。
故答案为:(1)竖直匀速;(2)甲;(3)低;(4)增加物重。
20.【解答】解:(1)实验中要求用沿斜面向上的力拉着木块在斜面上做匀速直线运动,若物块沿斜面加速运动,则拉力变大,
由η=×100%=×100%可知,在物体重力G和斜面高度h、斜面长度s不变的情况下,斜面的机械效率偏小;
(2)第2次实验中斜面的机械效率为:η=×100%=×100%=×100%=50%;
(3)由表格数据可知,斜面长度为1m不变时,当斜面高度分别为0.2m、0.3m、0.4m时,斜面的机械效率依次为37.5%、50%、60%,
所以,斜面的高度h越大时斜面的机械效率越大,且斜面的机械效率先急剧增大,后缓慢增大,η与h的关系大概如图C所示;
(4)由表格数据可知,木块的重力和斜面长度为1m不变时,当斜面高度分别为0.2m、0.3m、0.4m时,拉力依次为1.6N、1.8N、2.0N,
所以,斜面的倾斜程度越缓越省力。
故答案为:(1)匀速直线;偏小;(2)50%;(3)C;(4)缓。
四.计算题(共2小题)
21.【解答】解:(1)工人做的有用功:
W有用=Gh=150N×10m=1500J;
(2)由图可知,n=2,不计绳重和摩擦,拉力F=(G+G动),
则动滑轮的重力;
G动=2F﹣G=2×100N﹣150N=50N;
(3)拉力端移动的距离:
s=nh=2×10m=20m,
拉力做的总功:
W总=Fs=100N×20m=2000J,
滑轮组的机械效率:
η==×100%=75%。
答:(1)工人做的有用功为1500J;
(2)动滑轮的重力为50N;
(3)滑轮组的机械效率为75%。
22.【解答】解:(1)由v=可得,20s内材料匀速提升的高度:
h=vt=0.5m/s×20s=10m,
由图可知,滑轮组绳子的有效股数n=3,则绳子自由端移动的距离:
s=nh=3×10m=30m,
20s内拉力所做的功:
W总=Fs=250N×30m=7500J;
(2)所做的有用功:
W有=Gh=500N×10m=5000J,
此滑轮组的机械效率:
η=×100%=×100%≈66.7%;
(3)不计绳重和摩擦,由F=(G+G动)可得,动滑轮的重力:
G动=nF﹣G=3×250N﹣500N=250N,
若绳子能承受的最大拉力为500N时,则提升物体的最大重力:
G大=nF大﹣G动=3×500N﹣250N=1250N,
此滑轮组的最大机械效率:
η大====×100%≈83.3%。
答:(1)20s内拉力所做的功为7500J;
(2)提升500N材料时,此滑轮组的机械效率是66.7%;
(3)若绳子能承受的最大拉力为500N时,此滑轮组的机械效率最大可提高到83.3%。
机械效率
一.选择题(共12小题)
1.下列关于功率、机械效率说法中,正确的是( )
A.机械效率越高,机械做功一定越快
B.做功越多的机械,机械效率越高
C.做功越快的机械,功率越大
D.功率越大的机械,做功一定越多
2.用如图重为G的均匀杠杆,先后把同一重物挂在A、B两处匀速提升相同高度,支点处的摩擦不计,下列说法正确的是( )
A.重物在A点处人做的有用功多
B.在提升重物时杠杆可节省距离
C.重物在A点处杠杆的机械效率更高
D.重物在B点处杠杆的机械效率更高
3.甲乙两个滑轮组如图所示,其中每一个滑轮的重量都相同,用它们在相同时间内分别将重物G1、G2提高相同的高度,不计绳重和摩擦,下列说法正确的是( )
A.若G1=G2,则拉力做的总功相同
B.若G1=G2,则甲机械效率大于乙机械效率
C.若F1=F2,则拉力做功的功率相同
D.用甲、乙中的任何一个滑轮组提起不同的重物,机械效率不变
4.如图所示,重800N的物体在100N水平拉力F的作用下,以0.1m/s的速度沿水平地面向左匀速直线运动了20s,滑轮组的机械效率为60%。在此过程中,下列说法正确的是( )
A.拉力F做的功为400J
B.物体与地面间的滑动摩擦力为180N
C.额外功的功率为6W
D.若物体的重力和运动速度不变,只增大水平地面的粗糙程度,则滑轮组的机械效率会降低
5.小明用如图所示的装置研究“杠杆的机械效率时,将重为G的钩码挂在铁质杠杆上A点,弹簧测力计作用于C点,竖直向上匀速拉动弹簧测力计,使钩码上升h高度,杠杆的机械效率为η1;在小明的装置基础上,小红仅改为将弹簧测力计作用于B点,竖直向上匀速拉动弹簧测力计,仍使钩码上升h高度,杠杆的机械效率为η2:在小明的装置基础上,小华仅改为将钩码挂到B点,竖直向上匀速拉动弹簧测力计,仍使钩码上升h高度,杠杆的机械效率为η3;则( )
A.η1<η2,η1<η3
B.η1=η2,η1<η3
C.η1=η2,η1=η3
D.η1>η2,η1>η3
6.如图所示,斜面长3m,高0.6m,小明用绳子在6s内将重50N的物体从其底端沿斜面向上匀速拉到顶端,拉力F是15N。下列说法中正确的是( )
A.斜面上的摩擦力是5N
B.拉力所做的功是30J
C.拉力做功的功率是5W
D.斜面的机械效率是80%
7.小明用动滑轮竖直向上提升重物,下列措施能提高动滑轮机械效率的是( )
A.减小动滑轮的重力
B.增大重物上升的高度
C.减小物体的重力
D.增大重物上升的速度
8.如图所示,在探究“斜面的机械效率”实验中,一下说法错误的是( )
A.木块沿斜面匀速上升的过程中,拉力和摩擦力是一对平衡力
B.用弹簧测力计沿着斜面向上拉木块时,应尽量匀速
C.斜面的倾斜程度影响斜面的机械效率
D.斜面的倾斜程度越小,所需的拉力越小
9.小明用如图所示的装置探究杠杆的机械效率,他将两个钩码悬挂在B点,在A点用弹簧测力计保持竖直方向拉动杠杆,使其绕O点缓慢转动,带动钩码上升一定的高度h(不计摩擦)( )
A.在杠杆转动过程中,弹簧测力计的示数会变小
B.仅将拉力的作用点从A点移到C点,杠杆的机械效率不变
C.仅增加钩码的个数,拉力所做的额外功增大
D.仅将钩码的悬挂点从B点移到C点,拉力做的总功变大
10.如图甲所示的装置,A是重10N的空吊篮,绳子B和C能承受的最大拉力分别为100N和60N。质量为50kg的小张同学将A提升到高处,施加的拉力F随时间变化关系如图乙所示,A上升的速度v随时间变化关系如图丙所示。忽略绳重及摩擦,(g=10N/kg)。下列结论正确的是( )
①动滑轮的重力为9N;
②0~1s内拉力F做的功为2.4J;
③1~2s内拉力F的功率为4W;
④此装置提升重物的最大机械效率约为81.8%。
A.①④
B.①③
C.②③④
D.③
11.如图所示,用相同的滑轮安装成甲、乙两种装置,分别用FA、FB匀速提升重力为GA、GB的
A、B两个物体。物体提升相同高度,不计绳重和摩擦,下列说法一定正确的是( )
A.若GA=GB,则η甲>η乙
B.若FA=FB,则η甲>η乙
C.若GA<GB,则FA>FB
D.若FA>FB,则GA<GB
12.如图,每个滑轮质量相同,重为G的物体,在拉力的作用下匀速上升,已知乙滑轮组的效率为η,不计摩擦、绳重和木板重,下列说法不正确是( )
A.两滑轮组的机械效率可能相等
B.F1一定大于F2
C.每个滑轮重
D.甲、乙将重物提升相同的高度时,拉力的功率可能相等
二.填空题(共6小题)
13.在实际生产劳动中使用机械时,总要做一些额外功,原因是任何机械本身都有
,并且机械零件与零件之间在发生相对运动时还存在着
,所以任何机械的机械效率总
100%(选填“大于”或“小于”)。
14.如图所示甲、乙两装置中所用滑轮相同,现分别用拉力F1、F2匀速提升重为G1、G2的两物体,不计绳重和摩擦。
(1)若F1=5N,G1=9N,则甲装置的机械效率是:
。
(2)若F1=F2,则甲装置的机械效率η甲
乙装置的机械效率η乙。(选填“大于”、“小于”或“等于”)
15.小明不小心将水桶掉入井中,用钩子将质量为1kg的桶从离井口5m的深处匀速捞到井口,称出桶内水的质量为9kg,这次捞桶的过程中,做的有用功是
J,额外功是
J,总功是
J,机械效率为
(g取10N/kg)。
16.如图所示,物体重180N,小明用100N的拉力(方向不变)将物体匀速提升2m,用了10s,则此过程中有用功
J,拉力的功率
W,滑轮组的机械效率
。
17.如图所示,弹簧测力计的示数为
N,钩码的重力为1.0N,钩码上升的高度h为0.1m,测力计竖直向上移动的距离s为0.3m,此时杠杆的机械效率为
。忽略杠杆转动轴的摩擦,仅将钩码的悬挂点从A移到B,若重物提升高度相同,则额外功与有用功的比值将
(增大/减小/不变),杠杆的机械效率将
。(增大/减小/不变)
18.如图,小明将一个重为3N的小车从斜面底端匀速拉到斜面顶端,沿斜面向上的拉力为1.25N,小车沿斜面移动的距离s=1.6m,上升的高度h=0.6m。则小明对小车做的有用功是
J,斜面的机械效率是
。
三.实验探究题(共2小题)
19.如图所示,“测滑轮组机械效率”的实验,实验得到的数据如表。
钩码重G/N
钩码上升高度h/m
绳端拉力F/N
绳端移动距离S/m
机械效率η
l
4
0.1
1.8
0.3
74%
2
4
0.1
1.4
0.5
57%
3
6
0.1
2.4
0.3
83%
(1)实验中应沿
拉动弹簧测力计,使钩码上升;
(2)从表中数据可分析出第1次是用
图的装置进行的实验;
(3)通过分析1,2次实验数据,可得结论:使用不同的滑轮组提升相同的重物时,动滑轮越重,滑轮组的机械效率越
(填“高”“低”);
(4)在第1次实验基础上,做了第3次实验,通过对比分析第1和第3次两次实验数据,可得结论:使用同一滑轮组,
可以提高滑轮组的机械效率。
20.为探究斜面的机械效率与斜面倾斜程度之间的关系,某探究小组的同学利用木块、木板、刻度尺、弹簧测力计等器材设计了如图所示的实验装置。实验测得的数据如下表:
实验次数
侧面倾斜程度
木块重力G/N
斜面高度h/m
沿斜面拉力F/N
斜面长度s/m
机械效率η
1
较缓
3
0.2
1.6
1
37.5%
2
较陡
3
0.3
1.8
1
3
最陡
3
0.4
2.0
1
60.0%
请你根据表中的数据解答下列问题:
(1)实验中要求用沿斜面向上的力拉着木块在斜面上做
运动,若木块沿斜面加速运动,则测得的机械效率
(选填“偏大”、“偏小”或“不变”)。
(2)第2次实验中,斜面的机械效率为
。
(3)当斜面长度一定时,斜面的机械效率η与斜面的高度h之间的关系大概如图
所示。
(4)从表格中我们还可以看出斜面的倾斜程度越
(选填“缓”或“陡”)越省力。
四.计算题(共2小题)
21.如图所示,工人用滑轮组在20s内匀速提起一个150N的物体,物体上升了10m,拉力F为100N,不计绳重与摩擦,求:
(1)工人做的有用功;
(2)动滑轮的重力;
(3)滑轮组的机械效率.
22.在九年级物理拓展课上,李博同学模拟某建筑工地上塔吊的工作情景,设置了如图所示的滑轮组来提升装修材料,若他用250N的拉力将500N的材料以0.5m/s匀速提升了20s,(不计绳重和摩擦,g=10N/kg)。求:
(1)20s内拉力所做的功;
(2)提升500N材料时,此滑轮组的机械效率是多少;
(3)若绳子能承受的最大拉力为500N时,设该最大拉力小于人的重力,此滑轮组的机械效率最大可提高到多少。
一.选择题(共12小题)
1.【解答】解:A、机械效率和功率两者没有因果关系,如滑轮组的机械效率可到80%,起重机的效率只有40%左右,但是起重机的功率却比滑轮组大的多。所以,机械效率高,功率不一定大,做功不一定快。故A错误;
B、根据W=Pt可知,做功的多少与时间和功率有关,只要时间长功率大,做功就多,与机械效率无关。故B错误;
C、做功快的机械,说明单位时间内完成的功多,所以功率一定大。故C正确;
D、根据W=Pt可知,做功的多少与时间和功率有关,若只是功率大,但时间短做功也不一定多。故D错误。
故选:C。
2.【解答】解:
A、利用杠杆提升重物时,所做的有用功为W有用=Gh,在A、B两处提升的是同一个重物,上升同样的高度,所以在A、B两处人做的有用功相同,故A错误;
B、根据力臂的定义,由图可知,动力臂大于阻力臂,则该杠杆为省力杠杆,费距离,故B错误;
CD、由图可知,在A、B两处提升重物,重物上升同样的高度时,杠杆的重心上升的高度hA>hB,
由W额外=G杆h可知,W额外A>W额外B,
在A、B两处人做的有用功相同,而W总=W有用+W额外,所以W总A>W总B,
由η=可知ηA<ηB.故C错误,D正确。
故选:D。
3.【解答】解:A、甲滑轮组中有一个动滑轮,乙滑轮组中有两个动滑轮,所以若把物体提升相同的高度,乙滑轮组做的额外功多,若G1=G2,把物体提升相同的高度,则根据W=Gh可知甲乙所做的有用功相同,总功=有用功+额外功,有用功一样,乙图额外功功大,所以乙的总功大于甲的总功,故A错误;
B、若G1=G2,甲乙所做的有用功相同,乙做的总功大于甲做的总功,根据η=,甲的机械效率大于乙的机械效率,故B正确;
C、若F1=F2,由于甲图有2段绳子承担物重,所以s=2h,乙图有3段绳子承担物重,所以s=3h,根据P==在相同时间内,甲的功率小于乙的功率,故C错误;
D、用同一个滑轮组提起不同的重物,所做的额外功不变,有用功发生变化,所以有用功在总功中的比值发生变化,所以机械效率变,故D错误。
故选:B。
4.【解答】解:A、由图知,n=3,则绳子自由端移动的距离:s=3s物=3v物t=3×0.1m/s×20s=6m,拉力做功为:W总=Fs绳=100N×6m=600J,故A错误;
B、因为η====,所以物体与地面间的滑动摩擦力:f=ηnF=60%×3×100N=180N,故B正确;
C、因为η=,所以有用功:W有=ηW总=60%×600J=360J,
额外功:W额=W总﹣W有=600J﹣360J=240J,
额外功做功的功率:P===12W,故C错误;
D、如果只增大接触面的粗糙程度,增大了摩擦力,增大了有用功,而额外功几乎不变,有用功与总功的比值变大,机械效率变大,故D错误。
故选:B。
5.【解答】解:
(1)原来弹簧测力计作用于C点,竖直向上匀速拉动弹簧测力计时,测得杠杆的机械效率η1;将弹簧测力计移动到B点时,仍将钩码竖直向上匀速提升相同的高度,根据W有用=Gh可知有用功不变;
因杠杆的偏转角度不变,则杠杆重心上升的高度不变,根据W额=G杠杆h杠杆可知,克服杠杆重和摩擦所做额外功不变;由于有用功和额外功都不变,所以总功也不变,根据η=×100%可知杠杆的机械效率不变,即η2=η1;
;
(2)根据图示可知,将钩码移动到B点时,阻力和动力臂都不变,阻力臂增大,由F1L1=F2L2可知,动力将增大,即F′>F;将钩码移至B点,提升相同高度,有用功相同,弹簧测力计竖直移动的距离不同,B点时杠杆上上升的高度小些,做的额外功小些,所以机械效率变大,即η1<η3。
故选:B。
6.【解答】解:(1)此过程所做有用功为:W有=Gh=50N×0.6m=30J;
拉力所做总功为:W总=Fs=15N×3m=45J;
故机械效率为:η===66.7%;
(2)拉力做功的功率为:P===7.5W;
(3)此过程所做额外功为:W额=W总﹣W有=45J﹣30J=15J;
由W额=fs变形得:
摩擦力为:f===5N。
故BCD错误,A正确。
故选:A。
7.【解答】解:
A、减小动滑轮的重力,在其他条件不变时,需要做的额外功减少,有用功不变,能提高动滑轮的机械效率,故A符合题意;
BD、动滑轮的机械效率η====,说明机械效率的高低与物体被提升的高度及上升速度无关,故BD不符合题意;
C、减小重物的重力,在其他条件不变时,所做的有用功会减少,额外功不变,这样有用功在总功中所占的比例就会降低,即动滑轮的机械效率降低,故C不符合题意。
故选:A。
8.【解答】解:A、木块在上升过程中受到重力、支持力、拉力和摩擦力四个力的作用,由于重力使物体有下滑的趋势,所以,要使物体匀速上升,拉力应大于摩擦力,拉力和摩擦力不是一对平衡力,故A错误;
B、为了保证弹簧测力计的示数稳定,需使木块受到的力为平衡力,则要让木块做匀速直线运动,故B正确;
C、其他条件一定时,斜面倾斜程度越大,机械效率越高,故C正确;
D、斜面的倾斜程度越小,越省力,沿斜面所用的拉力越小,故D正确。
故选:A。
9.【解答】解:A、若弹簧测力计拉力方向一直竖直向上拉动,阻力不变,动力臂减小,阻力臂变小,如下图所示:
△OBB′∽△OAA′,所以=,所以动力臂与阻力臂的比值不变,
因为阻力不变,根据杠杆的平衡条件知,弹簧测力计的示数应该不变,故A错误;
B、仅将拉力的作用点从A点移到C点,由于将相同的钩码提升相同的高度,有用功不变,额外功也不变,杠杆的机械效率不变,故B正确;
C、克服杠杆重力做的功为额外功,仅增加钩码的个数,杠杆重力和杠杆上升的高度不变,拉力所做的额外功不变,故C错误;
D、钩码的悬挂点在B点时,由杠杆的平衡条件得F1?OA=G?OB;悬挂点移至C点时,由杠杆的平衡条件得F2?OA=G?OC;从图中可以看出,由OB到OC力臂变大,所以弹簧测力计的示数变大,有用功不变,但杠杆提升的高度减小,额外功减小,又因为总功等于额外功与有用功之和,因此此次弹簧测力计做的功将小于第一次做的功,即仅将钩码的悬挂点从B点移到C点,拉力做的总功变小,故D错误。
故选:B。
10.【解答】解:
①由图丙可知,在1~2s内,A被匀速提升,由图乙可知拉力F=10N,
由图知,n=2,忽略绳重及摩擦,拉力F=(GA+G动),则动滑轮重力:G动=2F﹣GA=2×10N﹣10N=10N,故①错误;
②由图丙可知,0~1s内物体上升的距离:h=×0.2m/s×1s=0.1m,
则自由端移动的距离:s=2h=2×0.1m=0.2m,
由图乙可知,0~1s内拉力F=12N,
则0~1s内拉力F做的功:W=Fs=12N×0.2m=2.4J,故②正确;
③由图丙可知,A上升的速度vA=0.2m/s,拉力端移动速度v=2vA=2×0.2m/s=0.4m/s,
1~2s内拉力F的功率:P=Fv=10N×0.4m/s=4W,故③正确;
④忽略绳重及摩擦,C处绳子拉力FC=(FB+G动)=(FB+10N),
则当C处最大拉力为60N时,B处拉力为110N;
当B处最大拉力为100N时,C处拉力为55N;所以要以B处最大拉力为准,B处的拉力:FB=GA+G货物=100N,
此装置最多能匀速运载货物的重力:G货物=FB﹣GA=100N﹣10N=90N;
此装置提升重物的机械效率随提升物重的增大而增大,此装置提升重物的最大机械效率:
η=====×100%≈81.8%,故④正确。
故选:C。
11.【解答】解:
由图可知,甲滑轮组承重的绳子股数n甲=3,乙滑轮组承重的绳子股数n乙=2,
A、不计绳重和摩擦,克服物体重力做的功为有用功,克服物体重力和动滑轮重力做的功为总功,
则滑轮组的机械效率:η=×100%=×100%=×100%;
若GA=GB,由题知动滑轮重力相同,则η甲=η乙,故A错误;
B、由图可知,n甲=3,n乙=2,
由F=(G+G动)可得,提升物体的重力:G=nF﹣G动,
则两物体的重力分别为:GA=3FA﹣G动,GB=2FB﹣G动,
若FA=FB,由上式可知GA>GB,
根据η=×100%可知,则η甲>η乙,故B正确;
C、甲滑轮组绳子自由端的拉力F甲=(GA+G动),
乙滑轮组绳子自由端的拉力F乙=(GB+G动),
若GA<GB,则FA<FB,故C错误;
D、由B项解答可知,两物体的重力分别为:GA=3FA﹣G动,GB=2FB﹣G动,若FA>FB,由上式可知,无法判断GA与GB的大小关系,故D错误。
故选:B。
12.【解答】解:
(1)由图可知,甲滑轮组只有1个动滑轮,乙滑轮组有2个动滑轮,且不计摩擦、绳和木板的重,
因克服物体重力G做的功为有用功,克服物重和动滑轮重做的功为总功,
所以,两滑轮组的机械效率分别为:η甲==,η乙==,则η甲>η乙,故A错误;
由η乙=可得,动滑轮的重力(即每个滑轮重):
G动=,故C正确;
(2)由图可知,n甲=2,n乙=4,不计摩擦、绳和木板的重,
则两滑轮组绳子的拉力分别为:
F1=(G+G动)=(2G+2G动),F2=(G+2G动),
因(2G+2G动)>(G+2G动),
所以,F1>F2,故B正确;
甲、乙将重物提升相同的高度,拉力做功为总功,则F1与F2的功率分别为:
P甲==,P乙==,
因t甲和t乙的关系不确定,所以,F1与F2的功率可能相等,故D正确。
故选:A。
二.填空题(共6小题)
13.【解答】解:机械做功就要做额外功,额外功主要包括机械自身的重力和零件的摩擦,机械效率总小于1。
故答案为:重力、摩擦、小于。
14.【解答】解:
(1)由滑轮组的结构知道承担物重的绳子股数n甲=3,不计绳重和摩擦,甲装置的机械效率:
η=×100%=×100%=×100%=×100%=×100%=60%
(2)由图可知,乙图承担物重的绳子股数n乙=2,若F1=F2,由题知两装置中动滑轮重相同,不计绳重及摩擦,由拉力F=(G+G动),可知,G1>G2,
由η=×100%=×100%=×100%可知甲装置的机械效率η甲大于乙装置的机械效率η乙。
故答案为:60%;大于。
15.【解答】解:有用功为:W有=Gh=mgh=1kg×10N/kg×5m=50J;
该过程中是为了打捞水桶,对水桶中的水所做的功为额外功,额外功为:W额外=G水h=m水gh=9kg×10N/kg×5m=450J
总功为:W总=W有+W额外=50J+450J=500J
机械效率为:η===10%。
故答案为:50;450;500;10%。
16.【解答】解:(1)有用功:W有=Gh=180N×2m=360J;
(2)由图可知n=2,绳子自由端移动的距离s=nh=2×2m=4m,
拉力做的总功:W总=Fs=100N×4m=400J,
则拉力做功的功率:P===40W;
(3)滑轮组的机械效率:η=×100%=×100%=90%。
故答案为:360;40;90%。
17.【解答】解:
(1)由图可知,弹簧测力计的分度值是0.1N,所以它的示数是0.5N。
(2)在实验过程中,有用功是:W有=Gh=1.0N×0.1m=0.1J,
总功是:W总=Fs=0.5N×0.3m=0.15J,
所以杠杆的机械效率:η=×100%=×100%≈66.7%;
(3)杠杆提升钩码时,对钩码做有用功,克服杠杆重做额外功,并且W有+W额=W总;
设杠杆重心升高的距离为h,所以,Gh1+G杠h=Fh2,G不变,h1不变,G杠不变,
钩码从A点到B点,钩码还升高相同的高度,有用功不变;
杠杆上旋的角度减小,杠杆升高的距离h变小,克服杠杆重力所做的额外功变小,所以额外功与有用功的比值将减小;
因为Gh1+G杠h变小,所以Fh2也变小;根据η==可知,总功变小,有用功不变,所以η增大。
故答案为:0.5;
66.7%;减小;增大。
18.【解答】解:(1)小明对小车做的有用功:
W有=Gh=3N×0.6m=1.8J;
(2)拉力做的总功:
W总=Fs=1.25N×1.6m=2J,
斜面的机械效率为:
η==×100%=90%。
故答案为:1.8;90%。
三.实验探究题(共2小题)
19.【解答】解:
(1)实验中应该匀速竖直向上拉动弹簧测力计,以保证拉力大小恒定;
(2)实验1中,s1=0.3m,h1=0.1m,所以n1===3,所以实验1是用甲图做的实验;
(3)由表中第1次实验和第2次实验的数据可知,使用不同的滑轮组提升相同的重物时,动滑轮的个数越多(动滑轮的质量越大),滑轮组的机械效率越低;
(4)比较实验数据1和3可知,使用同一滑轮组,其他条件相同时,增大提升的物重,可以提高滑轮组的机械效率。
故答案为:(1)竖直匀速;(2)甲;(3)低;(4)增加物重。
20.【解答】解:(1)实验中要求用沿斜面向上的力拉着木块在斜面上做匀速直线运动,若物块沿斜面加速运动,则拉力变大,
由η=×100%=×100%可知,在物体重力G和斜面高度h、斜面长度s不变的情况下,斜面的机械效率偏小;
(2)第2次实验中斜面的机械效率为:η=×100%=×100%=×100%=50%;
(3)由表格数据可知,斜面长度为1m不变时,当斜面高度分别为0.2m、0.3m、0.4m时,斜面的机械效率依次为37.5%、50%、60%,
所以,斜面的高度h越大时斜面的机械效率越大,且斜面的机械效率先急剧增大,后缓慢增大,η与h的关系大概如图C所示;
(4)由表格数据可知,木块的重力和斜面长度为1m不变时,当斜面高度分别为0.2m、0.3m、0.4m时,拉力依次为1.6N、1.8N、2.0N,
所以,斜面的倾斜程度越缓越省力。
故答案为:(1)匀速直线;偏小;(2)50%;(3)C;(4)缓。
四.计算题(共2小题)
21.【解答】解:(1)工人做的有用功:
W有用=Gh=150N×10m=1500J;
(2)由图可知,n=2,不计绳重和摩擦,拉力F=(G+G动),
则动滑轮的重力;
G动=2F﹣G=2×100N﹣150N=50N;
(3)拉力端移动的距离:
s=nh=2×10m=20m,
拉力做的总功:
W总=Fs=100N×20m=2000J,
滑轮组的机械效率:
η==×100%=75%。
答:(1)工人做的有用功为1500J;
(2)动滑轮的重力为50N;
(3)滑轮组的机械效率为75%。
22.【解答】解:(1)由v=可得,20s内材料匀速提升的高度:
h=vt=0.5m/s×20s=10m,
由图可知,滑轮组绳子的有效股数n=3,则绳子自由端移动的距离:
s=nh=3×10m=30m,
20s内拉力所做的功:
W总=Fs=250N×30m=7500J;
(2)所做的有用功:
W有=Gh=500N×10m=5000J,
此滑轮组的机械效率:
η=×100%=×100%≈66.7%;
(3)不计绳重和摩擦,由F=(G+G动)可得,动滑轮的重力:
G动=nF﹣G=3×250N﹣500N=250N,
若绳子能承受的最大拉力为500N时,则提升物体的最大重力:
G大=nF大﹣G动=3×500N﹣250N=1250N,
此滑轮组的最大机械效率:
η大====×100%≈83.3%。
答:(1)20s内拉力所做的功为7500J;
(2)提升500N材料时,此滑轮组的机械效率是66.7%;
(3)若绳子能承受的最大拉力为500N时,此滑轮组的机械效率最大可提高到83.3%。
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
