11.2 与三角形有关的角 同步课时训练 2021--2022学年人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 11.2 与三角形有关的角 同步课时训练 2021--2022学年人教版八年级数学上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 480.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 22:03:09 | ||
图片预览


文档简介
人教版
八年级数学上册
11.2
与三角形有关的角
同步课时训练
一、选择题
1.
如图,∠A=60°,∠B=40°,则∠ACD的大小是( )
A.80°
B.90°
C.100°
D.110°
2.
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
A.
40°
B.
45°
C.
60°
D.
70°
3.
(2019?荆门)将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则的度数是
A.
B.
C.
D.
4.
如图,在△ABC中,D是∠ABC和∠ACB的平分线的交点,∠A=80°,∠ABD=30°,则∠BDC的度数为( )
A.100°
B.110°
C.120°
D.130°
5.
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A.
50°
B.
51°
C.
51.5°
D.
52.5°
6.
如图,将△ABC
沿BC向右平移后得到△DEF,∠A=65°,∠B=30°,则∠DFC的度数是( )
A.65°
B.35°
C.80°
D.85°
7.
(2019?大庆)如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是
A.15°
B.30°
C.45°
D.60°
8.
如图,把△ABC沿DE折叠,当点A落在四边形BCED内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,这个关系是( )
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
二、填空题
9.
如图,在△ABC中,∠A=85°,点D在BC的延长线上,∠ACD=140°,则∠B=________°.
10.
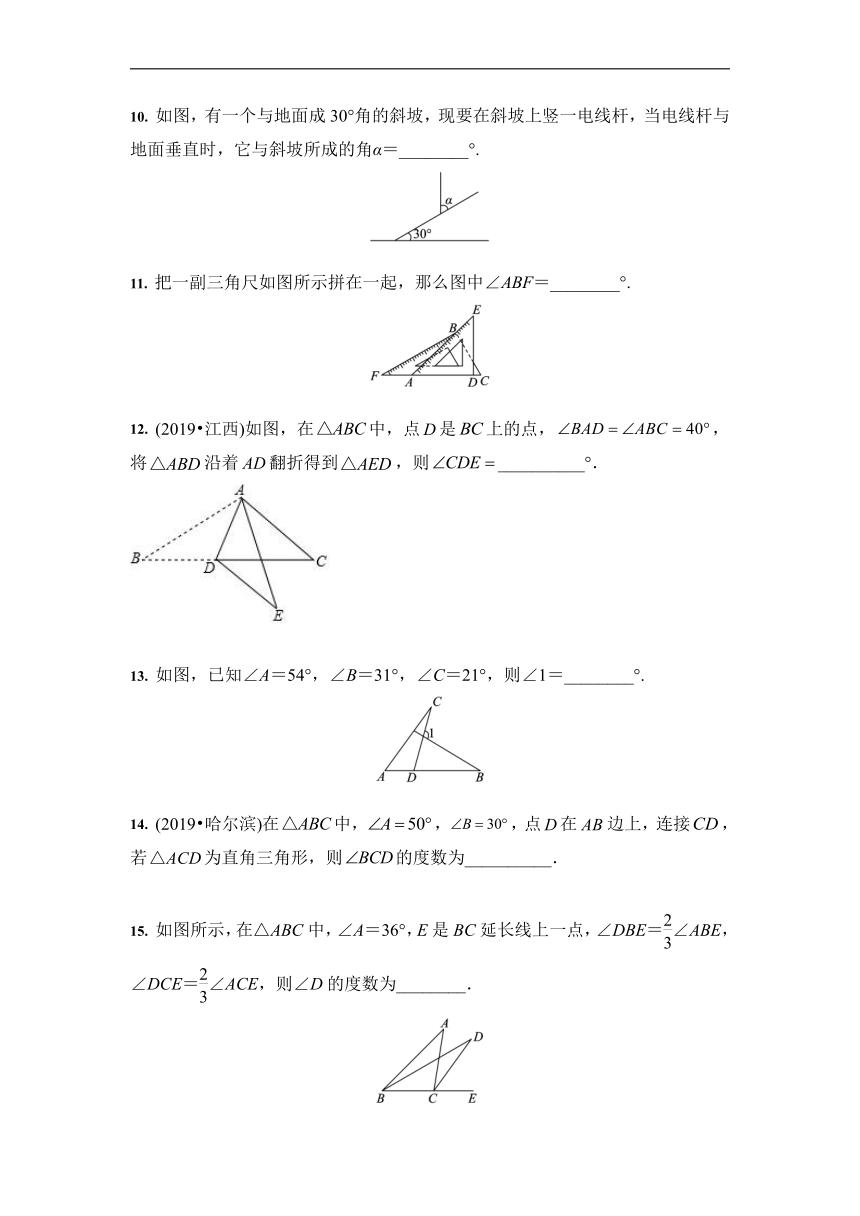
如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=________°.
11.
把一副三角尺如图所示拼在一起,那么图中∠ABF=________°.
12.
(2019?江西)如图,在中,点是上的点,,将沿着翻折得到,则__________°.
13.
如图,已知∠A=54°,∠B=31°,∠C=21°,则∠1=________°.
14.
(2019?哈尔滨)在中,,,点在边上,连接,若为直角三角形,则的度数为__________.
15.
如图所示,在△ABC中,∠A=36°,E是BC延长线上一点,∠DBE=∠ABE,∠DCE=∠ACE,则∠D的度数为________.
16.
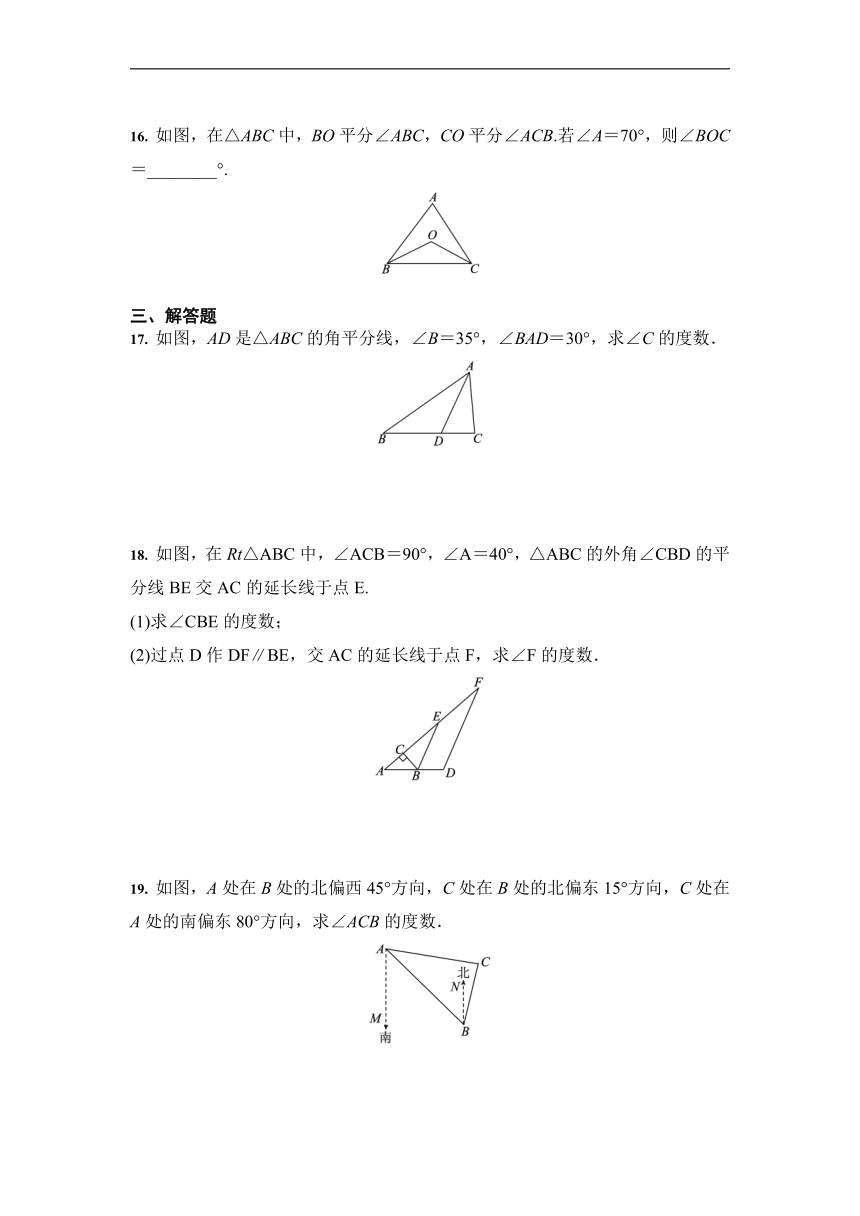
如图,在△ABC中,BO平分∠ABC,CO平分∠ACB.若∠A=70°,则∠BOC=________°.
三、解答题
17.
如图,AD是△ABC的角平分线,∠B=35°,∠BAD=30°,求∠C的度数.
18.
如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
19.
如图,A处在B处的北偏西45°方向,C处在B处的北偏东15°方向,C处在A处的南偏东80°方向,求∠ACB的度数.
20.
观察与转化思想如图是五角星形,求∠A+∠B+∠C+∠D+∠E的度数.
人教版
八年级数学上册
11.2
与三角形有关的角
同步课时训练-答案
一、选择题
1.
【答案】C
2.
【答案】A 【解析】由AE∥BD,可得∠DBC=∠E=35°,由BD平分∠ABC可得∠ABC=2∠DBC=70°,由AB=AC可得∠ABC=∠C=70°,由三角形内角和定理可得∠BAC=180°-70°-70°=40°.
3.
【答案】C
【解析】如图,
由题意得,,∴,
由三角形的外角性质可知,,故选C.
4.
【答案】D [解析]
∵BD是∠ABC的平分线,
∴∠DBC=∠ABD=30°,∠ABC=2∠ABD=2×30°=60°.
∴∠ACB=180°-∠A-∠ABC=40°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
∴∠BDC=180°-∠DCB-∠DBC=130°.
5.
【答案】D 【解析】∵AC=CD,∠A=50°,∴∠ADC=50°,∵DC=DB,∠ADC=∠B+∠BCD=50°,∴∠B=∠BCD=25°,∴∠BDC=130°,∵BD=BE,∴∠BED=∠BDE=77.5°,∴∠CDE=∠BDC-∠BDE=130°-77.5°=52.5°,故答案为D.
6.
【答案】D
7.
【答案】B
【解析】∵BE是∠ABC的平分线,∴∠EBM=∠ABC,
∵CE是外角∠ACM的平分线,∴∠ECM=∠ACM,
则∠BEC=∠ECM–∠EBM=×(∠ACM–∠ABC)=∠A=30°,故选B.
8.
【答案】B [解析]
因为∠A=180°-(∠B+∠C)=180°-(∠AED+∠ADE),所以∠B+∠C=∠AED+∠ADE.在四边形BCED中,∠1+∠2=360°-∠B-∠C-∠A′ED-∠A′DE=360°-(∠B+∠C)-(∠AED+∠ADE)=360°-2(180°-∠A),化简得∠1+∠2=2∠A.
二、填空题
9.
【答案】55
10.
【答案】60 [解析]
如图,延长电线杆与地面相交.
∵电线杆与地面垂直,
∴∠1=90°-30°=60°.
由对顶角相等,得α=∠1=60°.
11.
【答案】15 [解析]
由题意,得∠F=30°,∠EAD=45°.因为∠EAD=∠F+∠ABF,
所以∠ABF=∠EAD-∠F=15°.
12.
【答案】20
【解析】∵,将沿着翻折得到,
∴,,
∴,故答案为:20.
13.
【答案】106 [解析]
由三角形的外角性质可知,∠CDB=∠A+∠C=75°,
∴∠1=∠CDB+∠B=106°.
14.
【答案】或
【解析】分两种情况:
①如图1,当时,
∵,∴;
②如图2,当时,
∵,,∴,
∴,
综上,则的度数为或.故答案为:或.
15.
【答案】24° [解析]
∠D=∠DCE-∠DBE=∠ACE-∠ABE=(∠ACE-∠ABE)=∠A=×36°=24°.
16.
【答案】125 [解析]
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABO=∠CBO,∠BCO=∠ACO.
∴∠CBO+∠BCO=(∠ABC+∠ACB)=(180°-∠A)=(180°-70°)=55°.
∴在△BOC中,∠BOC=180°-55°=125°.
三、解答题
17.
【答案】
解:∵AD是△ABC的角平分线,
∴∠BAC=2∠BAD=2×30°=60°.
∴∠C=180°-∠B-∠BAC=180°-35°-60°=85°.
18.
【答案】
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,∴∠ABC=90°-∠A=50°.
∴∠CBD=130°.∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°.
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°-65°=25°.
∵DF∥BE,∴∠F=∠CEB=25°.
19.
【答案】
解:
由题意知∠ABN=45°,∠CBN=15°,∠MAC=80°,
所以∠ABC=60°.
因为AM∥BN,所以∠MAB=∠ABN=45°,
所以∠BAC=80°-45°=35°.
所以∠ACB=180°-60°-35°=85°.
20.
【答案】
解:如图,∵∠1是△CEG的外角,
∴∠1=∠C+∠E.
同理可得∠AFB=∠B+∠D.
∵在△AFG中,∠A+∠1+∠AFG=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
八年级数学上册
11.2
与三角形有关的角
同步课时训练
一、选择题
1.
如图,∠A=60°,∠B=40°,则∠ACD的大小是( )
A.80°
B.90°
C.100°
D.110°
2.
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
A.
40°
B.
45°
C.
60°
D.
70°
3.
(2019?荆门)将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则的度数是
A.
B.
C.
D.
4.
如图,在△ABC中,D是∠ABC和∠ACB的平分线的交点,∠A=80°,∠ABD=30°,则∠BDC的度数为( )
A.100°
B.110°
C.120°
D.130°
5.
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A.
50°
B.
51°
C.
51.5°
D.
52.5°
6.
如图,将△ABC
沿BC向右平移后得到△DEF,∠A=65°,∠B=30°,则∠DFC的度数是( )
A.65°
B.35°
C.80°
D.85°
7.
(2019?大庆)如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是
A.15°
B.30°
C.45°
D.60°
8.
如图,把△ABC沿DE折叠,当点A落在四边形BCED内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,这个关系是( )
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
二、填空题
9.
如图,在△ABC中,∠A=85°,点D在BC的延长线上,∠ACD=140°,则∠B=________°.
10.
如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=________°.
11.
把一副三角尺如图所示拼在一起,那么图中∠ABF=________°.
12.
(2019?江西)如图,在中,点是上的点,,将沿着翻折得到,则__________°.
13.
如图,已知∠A=54°,∠B=31°,∠C=21°,则∠1=________°.
14.
(2019?哈尔滨)在中,,,点在边上,连接,若为直角三角形,则的度数为__________.
15.
如图所示,在△ABC中,∠A=36°,E是BC延长线上一点,∠DBE=∠ABE,∠DCE=∠ACE,则∠D的度数为________.
16.
如图,在△ABC中,BO平分∠ABC,CO平分∠ACB.若∠A=70°,则∠BOC=________°.
三、解答题
17.
如图,AD是△ABC的角平分线,∠B=35°,∠BAD=30°,求∠C的度数.
18.
如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
19.
如图,A处在B处的北偏西45°方向,C处在B处的北偏东15°方向,C处在A处的南偏东80°方向,求∠ACB的度数.
20.
观察与转化思想如图是五角星形,求∠A+∠B+∠C+∠D+∠E的度数.
人教版
八年级数学上册
11.2
与三角形有关的角
同步课时训练-答案
一、选择题
1.
【答案】C
2.
【答案】A 【解析】由AE∥BD,可得∠DBC=∠E=35°,由BD平分∠ABC可得∠ABC=2∠DBC=70°,由AB=AC可得∠ABC=∠C=70°,由三角形内角和定理可得∠BAC=180°-70°-70°=40°.
3.
【答案】C
【解析】如图,
由题意得,,∴,
由三角形的外角性质可知,,故选C.
4.
【答案】D [解析]
∵BD是∠ABC的平分线,
∴∠DBC=∠ABD=30°,∠ABC=2∠ABD=2×30°=60°.
∴∠ACB=180°-∠A-∠ABC=40°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
∴∠BDC=180°-∠DCB-∠DBC=130°.
5.
【答案】D 【解析】∵AC=CD,∠A=50°,∴∠ADC=50°,∵DC=DB,∠ADC=∠B+∠BCD=50°,∴∠B=∠BCD=25°,∴∠BDC=130°,∵BD=BE,∴∠BED=∠BDE=77.5°,∴∠CDE=∠BDC-∠BDE=130°-77.5°=52.5°,故答案为D.
6.
【答案】D
7.
【答案】B
【解析】∵BE是∠ABC的平分线,∴∠EBM=∠ABC,
∵CE是外角∠ACM的平分线,∴∠ECM=∠ACM,
则∠BEC=∠ECM–∠EBM=×(∠ACM–∠ABC)=∠A=30°,故选B.
8.
【答案】B [解析]
因为∠A=180°-(∠B+∠C)=180°-(∠AED+∠ADE),所以∠B+∠C=∠AED+∠ADE.在四边形BCED中,∠1+∠2=360°-∠B-∠C-∠A′ED-∠A′DE=360°-(∠B+∠C)-(∠AED+∠ADE)=360°-2(180°-∠A),化简得∠1+∠2=2∠A.
二、填空题
9.
【答案】55
10.
【答案】60 [解析]
如图,延长电线杆与地面相交.
∵电线杆与地面垂直,
∴∠1=90°-30°=60°.
由对顶角相等,得α=∠1=60°.
11.
【答案】15 [解析]
由题意,得∠F=30°,∠EAD=45°.因为∠EAD=∠F+∠ABF,
所以∠ABF=∠EAD-∠F=15°.
12.
【答案】20
【解析】∵,将沿着翻折得到,
∴,,
∴,故答案为:20.
13.
【答案】106 [解析]
由三角形的外角性质可知,∠CDB=∠A+∠C=75°,
∴∠1=∠CDB+∠B=106°.
14.
【答案】或
【解析】分两种情况:
①如图1,当时,
∵,∴;
②如图2,当时,
∵,,∴,
∴,
综上,则的度数为或.故答案为:或.
15.
【答案】24° [解析]
∠D=∠DCE-∠DBE=∠ACE-∠ABE=(∠ACE-∠ABE)=∠A=×36°=24°.
16.
【答案】125 [解析]
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABO=∠CBO,∠BCO=∠ACO.
∴∠CBO+∠BCO=(∠ABC+∠ACB)=(180°-∠A)=(180°-70°)=55°.
∴在△BOC中,∠BOC=180°-55°=125°.
三、解答题
17.
【答案】
解:∵AD是△ABC的角平分线,
∴∠BAC=2∠BAD=2×30°=60°.
∴∠C=180°-∠B-∠BAC=180°-35°-60°=85°.
18.
【答案】
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,∴∠ABC=90°-∠A=50°.
∴∠CBD=130°.∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°.
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°-65°=25°.
∵DF∥BE,∴∠F=∠CEB=25°.
19.
【答案】
解:
由题意知∠ABN=45°,∠CBN=15°,∠MAC=80°,
所以∠ABC=60°.
因为AM∥BN,所以∠MAB=∠ABN=45°,
所以∠BAC=80°-45°=35°.
所以∠ACB=180°-60°-35°=85°.
20.
【答案】
解:如图,∵∠1是△CEG的外角,
∴∠1=∠C+∠E.
同理可得∠AFB=∠B+∠D.
∵在△AFG中,∠A+∠1+∠AFG=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
