13.1 轴对称 同步课时训练2021-2022学年人教版 八年级数学上册(Word版含答案)
文档属性
| 名称 | 13.1 轴对称 同步课时训练2021-2022学年人教版 八年级数学上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 686.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 22:04:34 | ||
图片预览


文档简介
人教版
八年级数学上册
13.1
轴对称
同步课时训练
一、选择题
1.
如图,在4×4的正方形网格中,已有四个小正方形被涂黑.若将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形,则该小正方形的位置可以是
( )
A.(一,2)
B.(二,4)
C.(三,2)
D.(四,4)
2.
如图,DE是△ABC中AB边的垂直平分线,若BC=6,AC=8,则△BCE的周长为( )
A.10
B.12
C.14
D.16
3.
若点A(2m,2-m)和点B(3+n,n)关于y轴对称,则m,n的值分别为( )
A.1,-1
B.,
C.-5,7
D.-,-
4.
如图,△ABC和△AB′C′关于直线l对称,下列结论中,错误的是( )
A.△ABC≌△AB′C′
B.∠BAC′=∠B′AC
C.l垂直平分点C,C′的连线
D.直线BC和B′C′的交点不在直线l上
5.
到三角形三个顶点的距离都相等的点是这个三角形的( )
A.
三条高线的交点
B.
三条角平分线的交点
C.
三条中线的交点
D.
三条边的垂直平分线的交点
6.
如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连接.若,,则的长为
A.
B.
C.
D.
7.
如图,以C为圆心,大于点C到AB的距离为半径作弧,交AB于点D,E,再以D,E为圆心,大于DE的长为半径作弧,两弧交于点F,作射线CF,则( )
A.CF平分∠ACB
B.CF⊥AB
C.CF平分AB
D.CF垂直平分AB
8.
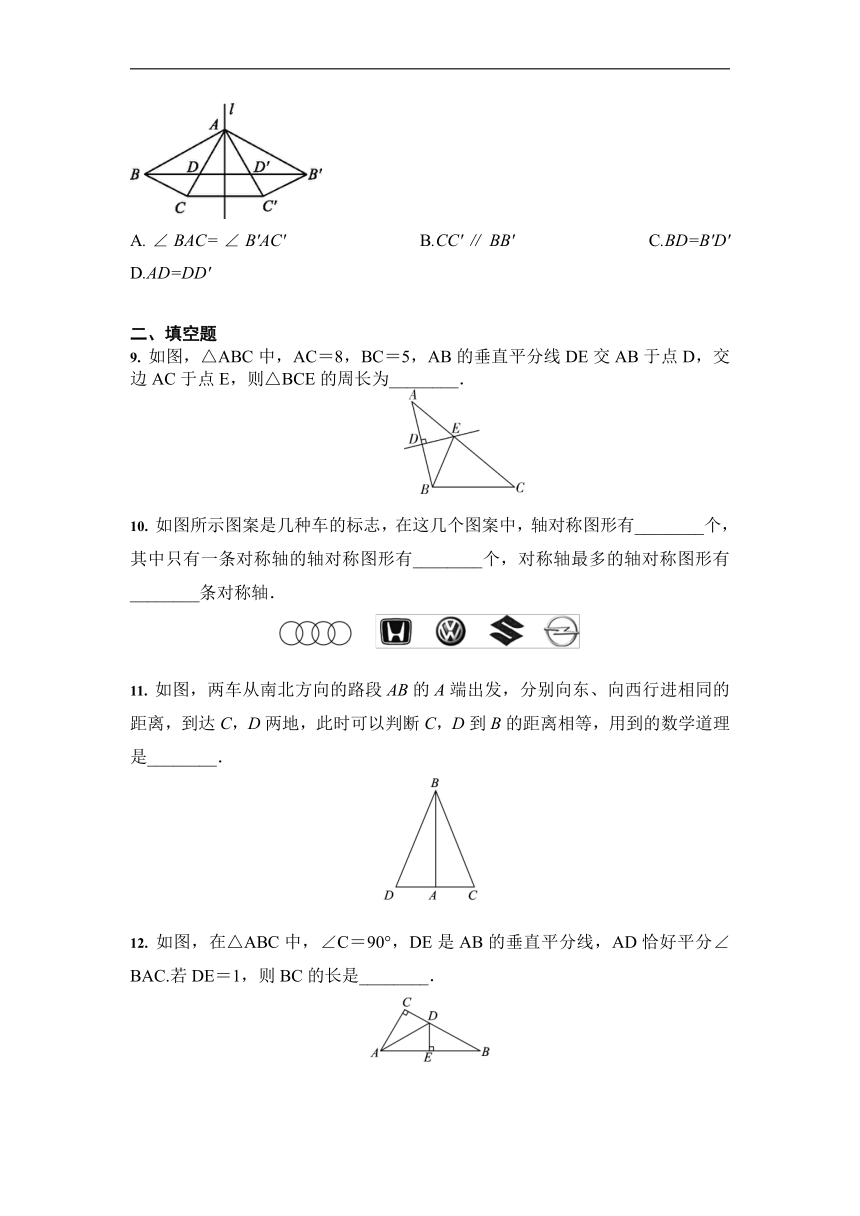
如图,点A在直线l上,△ABC与△AB'C'关于直线l对称,连接BB'分别交AC,AC'于点D,D',连接CC',下列结论不一定正确的是( )
A.∠BAC=∠B'AC'
B.CC'∥BB'
C.BD=B'D'
D.AD=DD'
二、填空题
9.
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
10.
如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.
11.
如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地,此时可以判断C,D到B的距离相等,用到的数学道理是________.
12.
如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.
13.
如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.
14.
画图:试画出下列正多边形的所有对称轴,并完成表格.
根据上表,猜想正n边形有 条对称轴.
15.
如图,在△ABC中,AB,AC的垂直平分线分别交BC于点E,F.若△AEF的周长为10
cm,则BC的长为 cm.?
16.
现要在三角地带ABC内(如图)建一座中心医院,使医院到A,B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请你确定这座中心医院的位置.
三、解答题
17.
如图,Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',其中
∠A=90°,AC=8
cm,点C,B,A'在同一条直线上,且A'C=12
cm.
(1)求△A'B'C'的周长;
(2)求△A'CC'的面积.
18.
如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,求线段DE的长.
19.
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
20.
如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG的周长为16,GE=3,求AC的长.
人教版
八年级数学上册
13.1
轴对称
同步课时训练-答案
一、选择题
1.
【答案】B [解析]
如图,把(二,4)位置的小正方形涂黑,则整个图案构成一个以直线AB为对称轴的轴对称图形.
2.
【答案】C [解析]
∵DE是△ABC中AB边的垂直平分线,∴AE=BE.∵BC=6,AC=8,∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=14.
3.
【答案】C [解析]
∵点A(2m,2-m)和点B(3+n,n)关于y轴对称,∴2m+3+n=0,2-m=n,解得m=-5,n=7.
4.
【答案】D
5.
【答案】D 【解析】依题意知这个点到三角形每边的两个端点的距离相等,∴它是三条边的垂直平分线的交点,故选D.
6.
【答案】A
【解析】由作法得垂直平分,
∴,,,
∵,∴,∴,
∴为斜边上的中线,
∵,
∴.故选A.
7.
【答案】B
8.
【答案】D [解析]
如图,设BB'交直线l于点O.
∵△ABC与△AB'C'关于直线l对称,
∴△ABC≌△AB'C',BB'⊥l,CC'⊥l,AB=AB',AC=AC',OD=OD',OB=OB'.
∴∠BAC=∠B'AC',BB'∥CC',BD=B'D'.
故选项A,B,C正确.故选D.
二、填空题
9.
【答案】13 【解析】∵DE垂直平分AB,∴AE=BE,∵AE+EC=8,∴EC+BE=8,∴△BCE的周长为BE+EC+BC=13.
10.
【答案】3 2 2
11.
【答案】线段垂直平分线上的点与这条线段两个端点的距离相等
12.
【答案】3 [解析]
∵AD平分∠BAC,且DE⊥AB,∠C=90°,∴CD=DE=1.
∵DE是AB的垂直平分线,∴AD=BD.
∴∠B=∠DAB.
∵∠DAB=∠CAD,
∴∠CAD=∠DAB=∠B.
∵∠C=90°,∴∠CAD+∠DAB+∠B=90°.
∴∠B=30°.∴BD=2DE=2.
∴BC=BD+CD=2+1=3.
13.
【答案】5
14.
【答案】解:如图.
故填3,4,5,6,n.
15.
【答案】10 [解析]
∵AB,AC的垂直平分线分别交BC于点E,F,∴AE=BE,AF=CF.
∴BC=BE+EF+CF=AE+EF+AF=10
cm.
16.
【答案】解:作线段AB的垂直平分线EF,作∠BAC的平分线AM,EF与AM相交于点P,则点P处即为这座中心医院的位置.
三、解答题
17.
【答案】
解:(1)∵Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',AC=8
cm,A'C=8cm,
∴AB=A'B',AC=A'C',∠A'=∠A=90°.
∴△A'B'C'的周长为A'C'+B'C'+A'B'=AC+A'C=12+8=20(cm).
(2)由(1)得A'C'=AC=8
cm,∠A'=90°,
∴△A'CC'的面积为A'C·A'C'=×12×8=48(cm2).
18.
【答案】
解:∵BC边的垂直平分线DE交边BC于点D,交边AB于点E,
∴BE=EC,BD=CD.
∵△EDC的周长为24,
∴DE+EC+CD=24.
∴DE+BE+BD=24.①
∵△ABC与四边形AEDC的周长之差为12,
∴(AE+BE+BD+CD+AC)-(AE+DE+CD+AC)=12,
∴BE+BD-DE=12.②
由①-②,得2DE=12,
∴DE=6.
19.
【答案】
解:(1)证明:在长方形ABCD中,DA=BC,∠A=∠D=∠B=∠BCD=90°.由折叠的性质,得GC=DA,∠G=∠D=90°,∠GCE=∠A=90°.
∴GC=BC,∠GCF+∠FCE=90°,∠FCE+∠BCE=90°.
∴∠GCF=∠BCE.
又∵∠G=∠B=90°,GC=BC,
∴△FGC≌△EBC(ASA).
(2)由(1)知,DF=GF=BE,
∴S四边形ECGF=S△FGC+S△EFC=S△EBC+S△EFC=S四边形BCFE====16.
20.
【答案】
解:∵DE垂直平分线段AB,GF垂直平分线段BC,
∴EB=EA,GB=GC.
∵△BEG的周长为16,
∴EB+GB+GE=16.
∴EA+GC+GE=16.
∴GA+GE+GE+GE+EC=16.
∴AC+2GE=16.
∵GE=3,
∴AC=10.
八年级数学上册
13.1
轴对称
同步课时训练
一、选择题
1.
如图,在4×4的正方形网格中,已有四个小正方形被涂黑.若将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形,则该小正方形的位置可以是
( )
A.(一,2)
B.(二,4)
C.(三,2)
D.(四,4)
2.
如图,DE是△ABC中AB边的垂直平分线,若BC=6,AC=8,则△BCE的周长为( )
A.10
B.12
C.14
D.16
3.
若点A(2m,2-m)和点B(3+n,n)关于y轴对称,则m,n的值分别为( )
A.1,-1
B.,
C.-5,7
D.-,-
4.
如图,△ABC和△AB′C′关于直线l对称,下列结论中,错误的是( )
A.△ABC≌△AB′C′
B.∠BAC′=∠B′AC
C.l垂直平分点C,C′的连线
D.直线BC和B′C′的交点不在直线l上
5.
到三角形三个顶点的距离都相等的点是这个三角形的( )
A.
三条高线的交点
B.
三条角平分线的交点
C.
三条中线的交点
D.
三条边的垂直平分线的交点
6.
如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连接.若,,则的长为
A.
B.
C.
D.
7.
如图,以C为圆心,大于点C到AB的距离为半径作弧,交AB于点D,E,再以D,E为圆心,大于DE的长为半径作弧,两弧交于点F,作射线CF,则( )
A.CF平分∠ACB
B.CF⊥AB
C.CF平分AB
D.CF垂直平分AB
8.
如图,点A在直线l上,△ABC与△AB'C'关于直线l对称,连接BB'分别交AC,AC'于点D,D',连接CC',下列结论不一定正确的是( )
A.∠BAC=∠B'AC'
B.CC'∥BB'
C.BD=B'D'
D.AD=DD'
二、填空题
9.
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
10.
如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.
11.
如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地,此时可以判断C,D到B的距离相等,用到的数学道理是________.
12.
如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.
13.
如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.
14.
画图:试画出下列正多边形的所有对称轴,并完成表格.
根据上表,猜想正n边形有 条对称轴.
15.
如图,在△ABC中,AB,AC的垂直平分线分别交BC于点E,F.若△AEF的周长为10
cm,则BC的长为 cm.?
16.
现要在三角地带ABC内(如图)建一座中心医院,使医院到A,B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请你确定这座中心医院的位置.
三、解答题
17.
如图,Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',其中
∠A=90°,AC=8
cm,点C,B,A'在同一条直线上,且A'C=12
cm.
(1)求△A'B'C'的周长;
(2)求△A'CC'的面积.
18.
如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,求线段DE的长.
19.
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
20.
如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG的周长为16,GE=3,求AC的长.
人教版
八年级数学上册
13.1
轴对称
同步课时训练-答案
一、选择题
1.
【答案】B [解析]
如图,把(二,4)位置的小正方形涂黑,则整个图案构成一个以直线AB为对称轴的轴对称图形.
2.
【答案】C [解析]
∵DE是△ABC中AB边的垂直平分线,∴AE=BE.∵BC=6,AC=8,∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=14.
3.
【答案】C [解析]
∵点A(2m,2-m)和点B(3+n,n)关于y轴对称,∴2m+3+n=0,2-m=n,解得m=-5,n=7.
4.
【答案】D
5.
【答案】D 【解析】依题意知这个点到三角形每边的两个端点的距离相等,∴它是三条边的垂直平分线的交点,故选D.
6.
【答案】A
【解析】由作法得垂直平分,
∴,,,
∵,∴,∴,
∴为斜边上的中线,
∵,
∴.故选A.
7.
【答案】B
8.
【答案】D [解析]
如图,设BB'交直线l于点O.
∵△ABC与△AB'C'关于直线l对称,
∴△ABC≌△AB'C',BB'⊥l,CC'⊥l,AB=AB',AC=AC',OD=OD',OB=OB'.
∴∠BAC=∠B'AC',BB'∥CC',BD=B'D'.
故选项A,B,C正确.故选D.
二、填空题
9.
【答案】13 【解析】∵DE垂直平分AB,∴AE=BE,∵AE+EC=8,∴EC+BE=8,∴△BCE的周长为BE+EC+BC=13.
10.
【答案】3 2 2
11.
【答案】线段垂直平分线上的点与这条线段两个端点的距离相等
12.
【答案】3 [解析]
∵AD平分∠BAC,且DE⊥AB,∠C=90°,∴CD=DE=1.
∵DE是AB的垂直平分线,∴AD=BD.
∴∠B=∠DAB.
∵∠DAB=∠CAD,
∴∠CAD=∠DAB=∠B.
∵∠C=90°,∴∠CAD+∠DAB+∠B=90°.
∴∠B=30°.∴BD=2DE=2.
∴BC=BD+CD=2+1=3.
13.
【答案】5
14.
【答案】解:如图.
故填3,4,5,6,n.
15.
【答案】10 [解析]
∵AB,AC的垂直平分线分别交BC于点E,F,∴AE=BE,AF=CF.
∴BC=BE+EF+CF=AE+EF+AF=10
cm.
16.
【答案】解:作线段AB的垂直平分线EF,作∠BAC的平分线AM,EF与AM相交于点P,则点P处即为这座中心医院的位置.
三、解答题
17.
【答案】
解:(1)∵Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',AC=8
cm,A'C=8cm,
∴AB=A'B',AC=A'C',∠A'=∠A=90°.
∴△A'B'C'的周长为A'C'+B'C'+A'B'=AC+A'C=12+8=20(cm).
(2)由(1)得A'C'=AC=8
cm,∠A'=90°,
∴△A'CC'的面积为A'C·A'C'=×12×8=48(cm2).
18.
【答案】
解:∵BC边的垂直平分线DE交边BC于点D,交边AB于点E,
∴BE=EC,BD=CD.
∵△EDC的周长为24,
∴DE+EC+CD=24.
∴DE+BE+BD=24.①
∵△ABC与四边形AEDC的周长之差为12,
∴(AE+BE+BD+CD+AC)-(AE+DE+CD+AC)=12,
∴BE+BD-DE=12.②
由①-②,得2DE=12,
∴DE=6.
19.
【答案】
解:(1)证明:在长方形ABCD中,DA=BC,∠A=∠D=∠B=∠BCD=90°.由折叠的性质,得GC=DA,∠G=∠D=90°,∠GCE=∠A=90°.
∴GC=BC,∠GCF+∠FCE=90°,∠FCE+∠BCE=90°.
∴∠GCF=∠BCE.
又∵∠G=∠B=90°,GC=BC,
∴△FGC≌△EBC(ASA).
(2)由(1)知,DF=GF=BE,
∴S四边形ECGF=S△FGC+S△EFC=S△EBC+S△EFC=S四边形BCFE====16.
20.
【答案】
解:∵DE垂直平分线段AB,GF垂直平分线段BC,
∴EB=EA,GB=GC.
∵△BEG的周长为16,
∴EB+GB+GE=16.
∴EA+GC+GE=16.
∴GA+GE+GE+GE+EC=16.
∴AC+2GE=16.
∵GE=3,
∴AC=10.
