12.2 一次函数 同步练习 2021—2022学年沪科版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 12.2 一次函数 同步练习 2021—2022学年沪科版八年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 232.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 22:09:17 | ||
图片预览




文档简介
12.2一次函数
基础强化
一、选择题
1.下列函数(1)y=x;(2)y=2x-1;(3)y=;(4)y=x2-1中,是一次函数的有(
)
A.4个
B.3个
C.2个
D.1个
2.一次函数y=2x-3的图象不经过的象限是(
?
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.下列说法正确的是(??
)
A.?正比例函数是一次函数?????B.?一次函数是正比例函数
C.?正比例函数不是一次函数???D.?不是正比例函数就不是一次函数
4.将函数y=x+2的图象用下列方法平移后,所得的图象经过点A(1,4)的方法是( )
A.向左平移1个单位
B.向右平移3个单位
C.向上平移1个单位
D.向下平移1个单位
5.如图所示的计算程序中,y与x之间的函数关系所对应的图象应为(
)
6.已知函数y=kx+b的图象如图,则k和b分别是(
?
)
A.k=1,b=-1;
B.k=-1,b=-1;
C.k=-1,b=1
;
D.k=1,b=1
7.已知点A(﹣2,y1),B(3,y2)在一次函数y=﹣x﹣2的图象上,则(????
)
A.?y1>y2??
B.?y1<y2?????C.?y1≤y2????D.?y1≥y2
8.小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完;销售金额与卖瓜千克数之间的关系如图所示,那么小李赚了()
A.32元
B.36元
C.38元
D.44元
9.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法:
(1)他们都骑行了20km;??????
(2)乙在途中停留了0.5h;
(3)甲、乙两人同时到达目的地;
(4)相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有(?
).
A. 1个??
B. 2个??????
C. 3个???????
D. 4个
已知一次函数y=2x+m-3和y=3x-m-1的图像相交于x轴上同一点,则m的值为(
)
A.???
B. ????
C. 1?????
D.
二、填空题
11.已知函数y=4-2x的图象经过(1,a),则a的值是_____________.
12.已知一次函数y=kx-5(k为常数,k≠0)的图象经过第二、三、四象限,写出一个符合条件的k的值: .?
13.已知函数y=(m-1)x+m2-1是正比例函数,则m=_____________.
14.已知函数满足下列两个条件:
①x>0时,y随x的增大而增大;
②它的图象经过点(1,2).
请写出一个符合上述条件的函数的表达式________.
15.已知直线与直线平行,且过点(2,1),则
,b=
16.已知与成正比例,当时,。则当时,的值为
。
三、简答题
17.一次函数的图象经过(-2,1)和(1,4)两点.
(1)求这个一次函数的解析式;
(2)当x=3时,求y的值.
18.在同一直角坐标系中画出一次函数y1=-2x+1与y2=2x-3的图象,并根据图象解答下列问题:
(1)直线y1=-x+1、y2=2x-2与y轴分别交于点A、B,请写出A、B两点的坐标;
(2)写出直线y1=-2x+1与y2=2x-3的交点P的坐标;
(3)求△PAB的面积.
19.声音在空气中传播的速度y(米/秒)(简称音速)是气温x(℃)的一次函数,下表列出了一组不同气温的音速.
气温x(℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
(1)求y与x的函数关系式;
(2)气温22
℃时,某人看到烟花燃放5秒后才听到响声,那么此人与燃放烟花所在地约相距多少米?
已知一次函数的图象过点A(1,4),B(-1,0)两点,求该函数的解析式,并画出它的图像,利用图像解答下列问题:
(1)当x为何值时,y>0,y=0,y<0
(2)当-3<x<0时,求y的取值范围
(3)当-2≤y≤2时,求x的取值范围
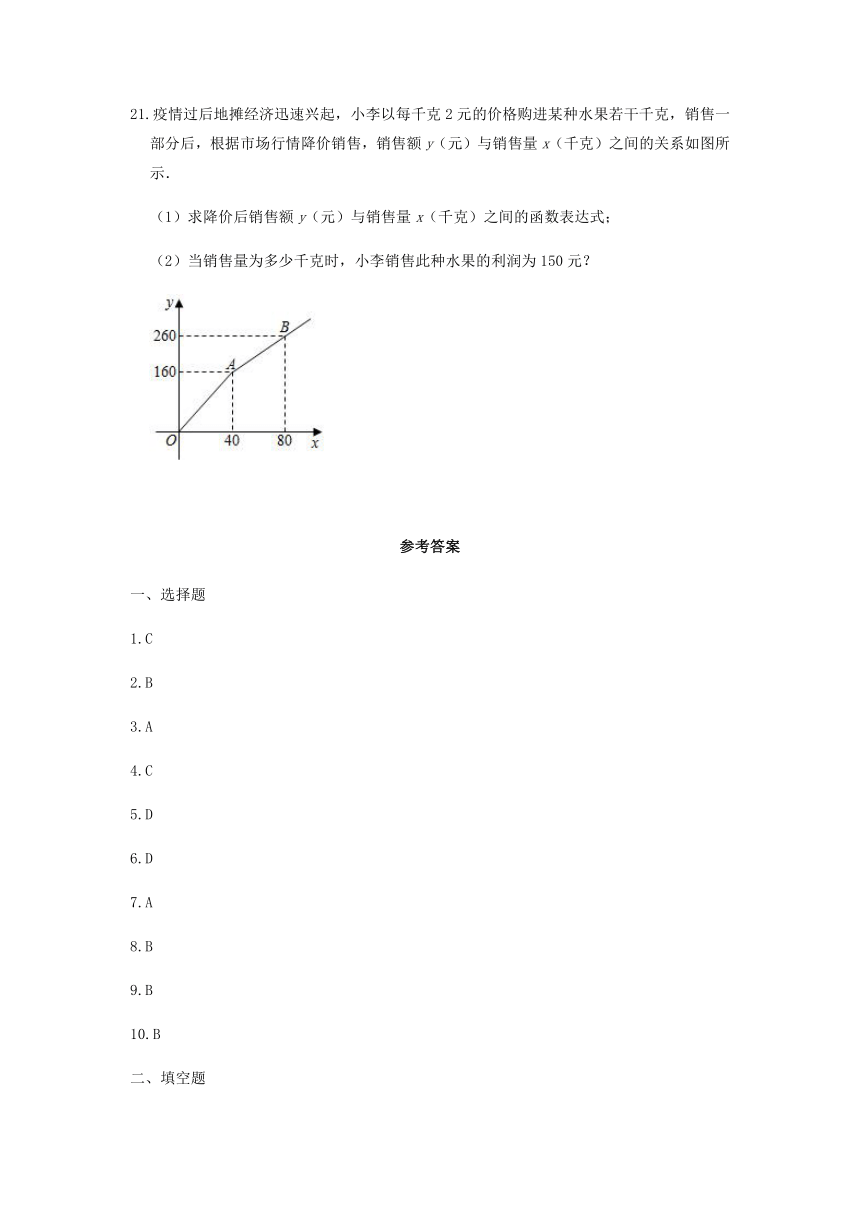
21.疫情过后地摊经济迅速兴起,小李以每千克2元的价格购进某种水果若干千克,销售一部分后,根据市场行情降价销售,销售额y(元)与销售量x(千克)之间的关系如图所示.
(1)求降价后销售额y(元)与销售量x(千克)之间的函数表达式;
(2)当销售量为多少千克时,小李销售此种水果的利润为150元?
参考答案
一、选择题
1.C
2.B
3.A
4.C
5.D
6.D
7.A
8.B
9.B
10.B
二、填空题
11.2;12.k为负数即可;13.-1;14.y=x+1(答案不唯一);
15.,2;
16.-4
三、简答题
17.解:(1)设这个一次函数的解析式为y=kx+b(k≠0).
∵该函数图象经过(-2,1)和(1,4)两点,
∴解得
∴这个一次函数的解析式为y=x+3.
(2)当x=3时,y=3+3=6.
18.①∵直线y1=-x+1、y2=2x-2与y轴分别交于点A、B,
∴x=0时,y1=1,x=0时,y2=-2,
∴A(0,1)、B(0,-2);
②如图所示:直线y1=-2x+1与y2=2x-3的交点P的坐标为:P(1,-1);
③△PAB的面积为:×AB×1=.
19.解:(1)设y=kx+b,则解得
∴y=x+331.
(2)当x=22时,y=×22+331=344.2米/秒,
344.2×5=1
721米.
即此人与燃放烟花所在地约相距1
721米.
20.解:设函数解析式为y=kx+b,把点A(1,4),B(-1,0)两点代入得,
k+b=4?k+b=0,
解得k=2b=2,
∴一次函数内的解析式为y=2x+2;
图象容如下:
(1)y=2x+2与x轴的交点为(-1,0),由图象可知:
当x>-1时,y>0,
当x=-1时,y=0,
当x<-1时,y<0;
(2)当x=-3时,y=-4,
当x=0时,y=2,
∴当-3<x<0时,-4<y<2;
(3)当y=-2时,x=-2,
当y=2时,x=0,
∴当-2≤y≤2时,-2<x<0.
21.解:(1)设降价后销售额y(元)与销售量x(千克)之间的函数表达式是y=kx+b,
∵AB段过点(40,160),(80,260),
∴,
解得,,
即降价后销售额y(元)与销售量x(千克)之间的函数表达式是y=2.5x+60(x>40);
(2)设当销售量为a千克时,小李销售此种水果的利润为150元,
2.5a+60﹣2a=150,
解得,a=180,
答:当销售量为180千克时,小李销售此种水果的利润为150元.
拓展培优
一、选择题
1.如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是(??
)
A.??????????B.?
C.?????????D.?
2.已知一次函数y=x+m与y=-x+n的图象都经过点A(-2,0),且分别与y轴交于点B,C,则△ABC的面积为( )
A.2
B.3
C.4
D.6
如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )
4.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离甲地的距离y(单位:km)与慢车行驶时间t(单位:h)的函数关系如图,则两车先后两次相遇的间隔时间是( )
A.h
B.h
C.h
D.h
5.为了提升城市品质,改善生态环境,落实民生实事,重庆市利用城市空地、荒地等修建了多个社区公园,为市民提供更多集休闲、娱乐、健身为一体的活动场所.一天晚饭后,小新和小达在小区附近的清溪公园散步,他们分别从公园入口和银杏林同时出发,匀速相向而行.小新到达银杏林后,放慢了速度,继续匀速向湖心亭前进,到达湖心亭后立即调头,以变慢后的速度匀速返回银杏林等待小达(公园入口、银杏林和湖心亭依次在同一直线上).小达走到公园入口后立即调头,以原速匀速返回银杏林与小新会合.小新和小达相距的路程y(米)与小达从银杏林出发的时间x(分)之间的函数关系如图所示(其中DE∥BG,B、C、D三点不在同一直线上,两人调头的时间忽略不计),
则下列4个说法:①a=22.5;②刚出发时,小新的速度为80米/分;③图象中线段DE表示小新和小达两人停止了运动;④公园入口到湖心亭的距离为2250米,其中正确说法的个数是( )
A.1
B.2
C.3
D.4
二、填空题
6.已知直线y=2x+(3-a)与x轴的交点在A(2,0),B(3,0)之间(包括A,B两点),则a的取值范围是
.
7.如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是________.
如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是
.
?
9.直线经过点A(-1,-2)和点B(-2,0)则关于的不等式组的解集为
。
10.如图,在平面直角坐标系中,点A1,A2,A3,…,An在x轴上,B1,B2,B3,…,Bn在直线y=x上,若A1(2,0),且△A1B1A2,△A2B2A3,…,△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1,S2,S3,…,Sn.则Sn可表示为
.
三、解答题
11.“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为y(米)与时间x(分钟)的关系如图.请结合图象,解答下列问题:
(1)填空:a=
;b=
;m=
.
(2)求线段BC所在直线的解析式.
(3)若小军的速度是120米/分,求小军第二次与爸爸相遇时距图书馆的距离.
12.
已知一水池的容积(公升)与注入水的时间(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间(分钟)
0
10
…
25
水池的容积(公升)
100
300
…
600
(1)求这段时间时关于的函数关系式(不需要写出函数的定义域);
(2)从为25分钟开始,每分钟注入的水量发生变化了,到为27分钟时,水池的容积为公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
13.一水池现储水20立方米,用水管以5立方米/时的速度向水池注水,同时另一排水管以6立方米/时的速度向水池外排水.
(1)写出水池蓄水量V(米3)与进水时间t(时)之间的关系式(注意自变量的取值范围);
(2)何时水池中的水被排空?
14.有两条直线l1:y=ax+b和l2:y=cx+5.学生甲解出它们的交点为(3,-2);学生乙因把c抄错了而解出它们的交点为,试写出这两条直线的解析式.
参考答案
一、选择题
1.B
2.C
3.C
4.B
5.B
二、填空题
6.7≤a≤9
7.10
8.48
9.
10..
三、解答题
11.解:(1)由图可得,
a=1500÷150=10,b=10+5=15,m=(3000﹣1500)÷(22.5﹣15)=1500÷7.5=200,
故答案为:10,15,200;
(2)设线段BC所在的直线的解析式为y=kx+m,
∵点B(15,1500),点C(22.5,3000)在直线y=kx+m上,
∴,得
即线段BC所在的直线的解析式为y=200x﹣1500;
(3)∵小军的速度是120米/分,
∴线段OD所在直线的解析式为y=120x,
令120x=200x﹣1500,
解得,x=18.75
∴小军第二次与爸爸相遇时距图书馆的距离是3000﹣120×18.75=750(米),
答:小军第二次与爸爸相遇时距图书馆的距离是750米.
12.解:(1)设关于的函数解析式为:
由题意得:
解此方程组得:
所以关于的函数解析式为:
(2)设这个百分率为
由题意得:
解此方程得:,(不符合题意舍去)
答这个百分率为.
13.(1)V=20+5t-6t=20-t(0≤t≤20);
(2)由题意得0=20-t,
解得t=20.
答:20小时后水池中的水被排空.
14.
基础强化
一、选择题
1.下列函数(1)y=x;(2)y=2x-1;(3)y=;(4)y=x2-1中,是一次函数的有(
)
A.4个
B.3个
C.2个
D.1个
2.一次函数y=2x-3的图象不经过的象限是(
?
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.下列说法正确的是(??
)
A.?正比例函数是一次函数?????B.?一次函数是正比例函数
C.?正比例函数不是一次函数???D.?不是正比例函数就不是一次函数
4.将函数y=x+2的图象用下列方法平移后,所得的图象经过点A(1,4)的方法是( )
A.向左平移1个单位
B.向右平移3个单位
C.向上平移1个单位
D.向下平移1个单位
5.如图所示的计算程序中,y与x之间的函数关系所对应的图象应为(
)
6.已知函数y=kx+b的图象如图,则k和b分别是(
?
)
A.k=1,b=-1;
B.k=-1,b=-1;
C.k=-1,b=1
;
D.k=1,b=1
7.已知点A(﹣2,y1),B(3,y2)在一次函数y=﹣x﹣2的图象上,则(????
)
A.?y1>y2??
B.?y1<y2?????C.?y1≤y2????D.?y1≥y2
8.小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完;销售金额与卖瓜千克数之间的关系如图所示,那么小李赚了()
A.32元
B.36元
C.38元
D.44元
9.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法:
(1)他们都骑行了20km;??????
(2)乙在途中停留了0.5h;
(3)甲、乙两人同时到达目的地;
(4)相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有(?
).
A. 1个??
B. 2个??????
C. 3个???????
D. 4个
已知一次函数y=2x+m-3和y=3x-m-1的图像相交于x轴上同一点,则m的值为(
)
A.???
B. ????
C. 1?????
D.
二、填空题
11.已知函数y=4-2x的图象经过(1,a),则a的值是_____________.
12.已知一次函数y=kx-5(k为常数,k≠0)的图象经过第二、三、四象限,写出一个符合条件的k的值: .?
13.已知函数y=(m-1)x+m2-1是正比例函数,则m=_____________.
14.已知函数满足下列两个条件:
①x>0时,y随x的增大而增大;
②它的图象经过点(1,2).
请写出一个符合上述条件的函数的表达式________.
15.已知直线与直线平行,且过点(2,1),则
,b=
16.已知与成正比例,当时,。则当时,的值为
。
三、简答题
17.一次函数的图象经过(-2,1)和(1,4)两点.
(1)求这个一次函数的解析式;
(2)当x=3时,求y的值.
18.在同一直角坐标系中画出一次函数y1=-2x+1与y2=2x-3的图象,并根据图象解答下列问题:
(1)直线y1=-x+1、y2=2x-2与y轴分别交于点A、B,请写出A、B两点的坐标;
(2)写出直线y1=-2x+1与y2=2x-3的交点P的坐标;
(3)求△PAB的面积.
19.声音在空气中传播的速度y(米/秒)(简称音速)是气温x(℃)的一次函数,下表列出了一组不同气温的音速.
气温x(℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
(1)求y与x的函数关系式;
(2)气温22
℃时,某人看到烟花燃放5秒后才听到响声,那么此人与燃放烟花所在地约相距多少米?
已知一次函数的图象过点A(1,4),B(-1,0)两点,求该函数的解析式,并画出它的图像,利用图像解答下列问题:
(1)当x为何值时,y>0,y=0,y<0
(2)当-3<x<0时,求y的取值范围
(3)当-2≤y≤2时,求x的取值范围
21.疫情过后地摊经济迅速兴起,小李以每千克2元的价格购进某种水果若干千克,销售一部分后,根据市场行情降价销售,销售额y(元)与销售量x(千克)之间的关系如图所示.
(1)求降价后销售额y(元)与销售量x(千克)之间的函数表达式;
(2)当销售量为多少千克时,小李销售此种水果的利润为150元?
参考答案
一、选择题
1.C
2.B
3.A
4.C
5.D
6.D
7.A
8.B
9.B
10.B
二、填空题
11.2;12.k为负数即可;13.-1;14.y=x+1(答案不唯一);
15.,2;
16.-4
三、简答题
17.解:(1)设这个一次函数的解析式为y=kx+b(k≠0).
∵该函数图象经过(-2,1)和(1,4)两点,
∴解得
∴这个一次函数的解析式为y=x+3.
(2)当x=3时,y=3+3=6.
18.①∵直线y1=-x+1、y2=2x-2与y轴分别交于点A、B,
∴x=0时,y1=1,x=0时,y2=-2,
∴A(0,1)、B(0,-2);
②如图所示:直线y1=-2x+1与y2=2x-3的交点P的坐标为:P(1,-1);
③△PAB的面积为:×AB×1=.
19.解:(1)设y=kx+b,则解得
∴y=x+331.
(2)当x=22时,y=×22+331=344.2米/秒,
344.2×5=1
721米.
即此人与燃放烟花所在地约相距1
721米.
20.解:设函数解析式为y=kx+b,把点A(1,4),B(-1,0)两点代入得,
k+b=4?k+b=0,
解得k=2b=2,
∴一次函数内的解析式为y=2x+2;
图象容如下:
(1)y=2x+2与x轴的交点为(-1,0),由图象可知:
当x>-1时,y>0,
当x=-1时,y=0,
当x<-1时,y<0;
(2)当x=-3时,y=-4,
当x=0时,y=2,
∴当-3<x<0时,-4<y<2;
(3)当y=-2时,x=-2,
当y=2时,x=0,
∴当-2≤y≤2时,-2<x<0.
21.解:(1)设降价后销售额y(元)与销售量x(千克)之间的函数表达式是y=kx+b,
∵AB段过点(40,160),(80,260),
∴,
解得,,
即降价后销售额y(元)与销售量x(千克)之间的函数表达式是y=2.5x+60(x>40);
(2)设当销售量为a千克时,小李销售此种水果的利润为150元,
2.5a+60﹣2a=150,
解得,a=180,
答:当销售量为180千克时,小李销售此种水果的利润为150元.
拓展培优
一、选择题
1.如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是(??
)
A.??????????B.?
C.?????????D.?
2.已知一次函数y=x+m与y=-x+n的图象都经过点A(-2,0),且分别与y轴交于点B,C,则△ABC的面积为( )
A.2
B.3
C.4
D.6
如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )
4.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离甲地的距离y(单位:km)与慢车行驶时间t(单位:h)的函数关系如图,则两车先后两次相遇的间隔时间是( )
A.h
B.h
C.h
D.h
5.为了提升城市品质,改善生态环境,落实民生实事,重庆市利用城市空地、荒地等修建了多个社区公园,为市民提供更多集休闲、娱乐、健身为一体的活动场所.一天晚饭后,小新和小达在小区附近的清溪公园散步,他们分别从公园入口和银杏林同时出发,匀速相向而行.小新到达银杏林后,放慢了速度,继续匀速向湖心亭前进,到达湖心亭后立即调头,以变慢后的速度匀速返回银杏林等待小达(公园入口、银杏林和湖心亭依次在同一直线上).小达走到公园入口后立即调头,以原速匀速返回银杏林与小新会合.小新和小达相距的路程y(米)与小达从银杏林出发的时间x(分)之间的函数关系如图所示(其中DE∥BG,B、C、D三点不在同一直线上,两人调头的时间忽略不计),
则下列4个说法:①a=22.5;②刚出发时,小新的速度为80米/分;③图象中线段DE表示小新和小达两人停止了运动;④公园入口到湖心亭的距离为2250米,其中正确说法的个数是( )
A.1
B.2
C.3
D.4
二、填空题
6.已知直线y=2x+(3-a)与x轴的交点在A(2,0),B(3,0)之间(包括A,B两点),则a的取值范围是
.
7.如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是________.
如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是
.
?
9.直线经过点A(-1,-2)和点B(-2,0)则关于的不等式组的解集为
。
10.如图,在平面直角坐标系中,点A1,A2,A3,…,An在x轴上,B1,B2,B3,…,Bn在直线y=x上,若A1(2,0),且△A1B1A2,△A2B2A3,…,△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1,S2,S3,…,Sn.则Sn可表示为
.
三、解答题
11.“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为y(米)与时间x(分钟)的关系如图.请结合图象,解答下列问题:
(1)填空:a=
;b=
;m=
.
(2)求线段BC所在直线的解析式.
(3)若小军的速度是120米/分,求小军第二次与爸爸相遇时距图书馆的距离.
12.
已知一水池的容积(公升)与注入水的时间(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间(分钟)
0
10
…
25
水池的容积(公升)
100
300
…
600
(1)求这段时间时关于的函数关系式(不需要写出函数的定义域);
(2)从为25分钟开始,每分钟注入的水量发生变化了,到为27分钟时,水池的容积为公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
13.一水池现储水20立方米,用水管以5立方米/时的速度向水池注水,同时另一排水管以6立方米/时的速度向水池外排水.
(1)写出水池蓄水量V(米3)与进水时间t(时)之间的关系式(注意自变量的取值范围);
(2)何时水池中的水被排空?
14.有两条直线l1:y=ax+b和l2:y=cx+5.学生甲解出它们的交点为(3,-2);学生乙因把c抄错了而解出它们的交点为,试写出这两条直线的解析式.
参考答案
一、选择题
1.B
2.C
3.C
4.B
5.B
二、填空题
6.7≤a≤9
7.10
8.48
9.
10..
三、解答题
11.解:(1)由图可得,
a=1500÷150=10,b=10+5=15,m=(3000﹣1500)÷(22.5﹣15)=1500÷7.5=200,
故答案为:10,15,200;
(2)设线段BC所在的直线的解析式为y=kx+m,
∵点B(15,1500),点C(22.5,3000)在直线y=kx+m上,
∴,得
即线段BC所在的直线的解析式为y=200x﹣1500;
(3)∵小军的速度是120米/分,
∴线段OD所在直线的解析式为y=120x,
令120x=200x﹣1500,
解得,x=18.75
∴小军第二次与爸爸相遇时距图书馆的距离是3000﹣120×18.75=750(米),
答:小军第二次与爸爸相遇时距图书馆的距离是750米.
12.解:(1)设关于的函数解析式为:
由题意得:
解此方程组得:
所以关于的函数解析式为:
(2)设这个百分率为
由题意得:
解此方程得:,(不符合题意舍去)
答这个百分率为.
13.(1)V=20+5t-6t=20-t(0≤t≤20);
(2)由题意得0=20-t,
解得t=20.
答:20小时后水池中的水被排空.
14.
