12.2 一次函数(正比例函数)同步练习 2021-2022学年沪科版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 12.2 一次函数(正比例函数)同步练习 2021-2022学年沪科版八年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 191.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 22:15:46 | ||
图片预览



文档简介
一次函数(正比例函数)
一、单选题
1.下列问题中,两个变量之间是正比例函数关系的是(
)
A.汽车以的速度匀速行驶,行驶路程与行驶时间之间的关系
B.圆的面积与它的半径之间的关系
C.某水池有水,现打开进水管进水,进水速度,后水池有水
D.有一个边长为x的正方体,则它的表面积S与边长x之间的函数关系
2.下列函数中,是正比例函数的是( )
A.y=x2
B.y=
C.y=
D.y=2x+3
3.若点在正比例函数的图象上,则k的值为(
)
A.
B.2
C.
D.
4.若正比例函数,当时,,则下列各点在该函数图象上的是(
)
A.
B.
C.
D.
5.在平面直角坐标系中,若一个正比例函数的图象经过A(5,b),B(a,4)两点,则a,b一定满足的关系式为(
)
A.a﹣b=1
B.a+b=9
C.a?b=20
D.=
6.正比例函数的图象经过的象限是( )
A.第一、三象限
B.第二、四象限
C.第一、四象限
D.第二、三象限
7.已知P1(x1,y1),P2(x2,y2)是正比例函数y=kx(k≠0)在第二象限的图象上的两个点,如果P1点在P2点左边,那么y1,y2的大小关系是( )
A.y1=y2
B.y1<y2
C.y1>y2
D.不能确定
8.正比例函数的图像如图所示,下列说法正确的是(
)
A.
B.随的增大而增大
C.
D.函数图像经过点
9.对于正比例函数,下列说法正确的是(
)
A.随的增大而减小
B.随的增大而增大
C.随的减小而增大
D.有最小值
10.P1(x1,y1),P2(x2,y2)是正比例函数y=﹣x图象上的两点,则下列判断正确的是( )
A.y1>y2
B.y1<y2
C.当x1<x2时,y1>y2
D.当x1<x2时,y1<y2
11.如果正比例函数y=(a﹣1)x(a是常数)的图象在第一、三象限,那么a的取值范围是( )
A.a<0
B.a>0
C.a<1
D.a>1
12.已知正比例函数y=(1﹣k)x.若函数值y随x的增大而减小,则实数k的值可能是( )
A.﹣1
B.0
C.1
D.
二、填空题
13.在y=3x﹣a﹣2中,若y是x的正比例函数,则常数a=_____.
14.已知,正比例函数y=kx的图象经过点(a,b),且=2,则k的值等于_______________.
15.若正比例函数y=kx的图象经过点A(k,9),且经过第一、三象限,则k的值是
___.
16.已知正比例函数,的值随的值增大而减小,那么的取值范围是______.
17.若正比例函数y=(1﹣2m)x的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时,y1>y2,则m的取值范围是__________________.
三、解答题
18.永安批发市场某天鸡蛋的价格为10元/kg.
(1)填写下表;
购买量/kg
0.5
1
2
?
付款金额/元
?
(2)写出付款金额y与购买量x(x≥0)的函数表达式.
19.已知函数,y=kx(k为常数且k≠0);
(1)当x=1,y=2时,则函数解析式为 ;
(2)当函数图象过第一、三象限时,k ;
(3)k ,y随x的增大而减小;
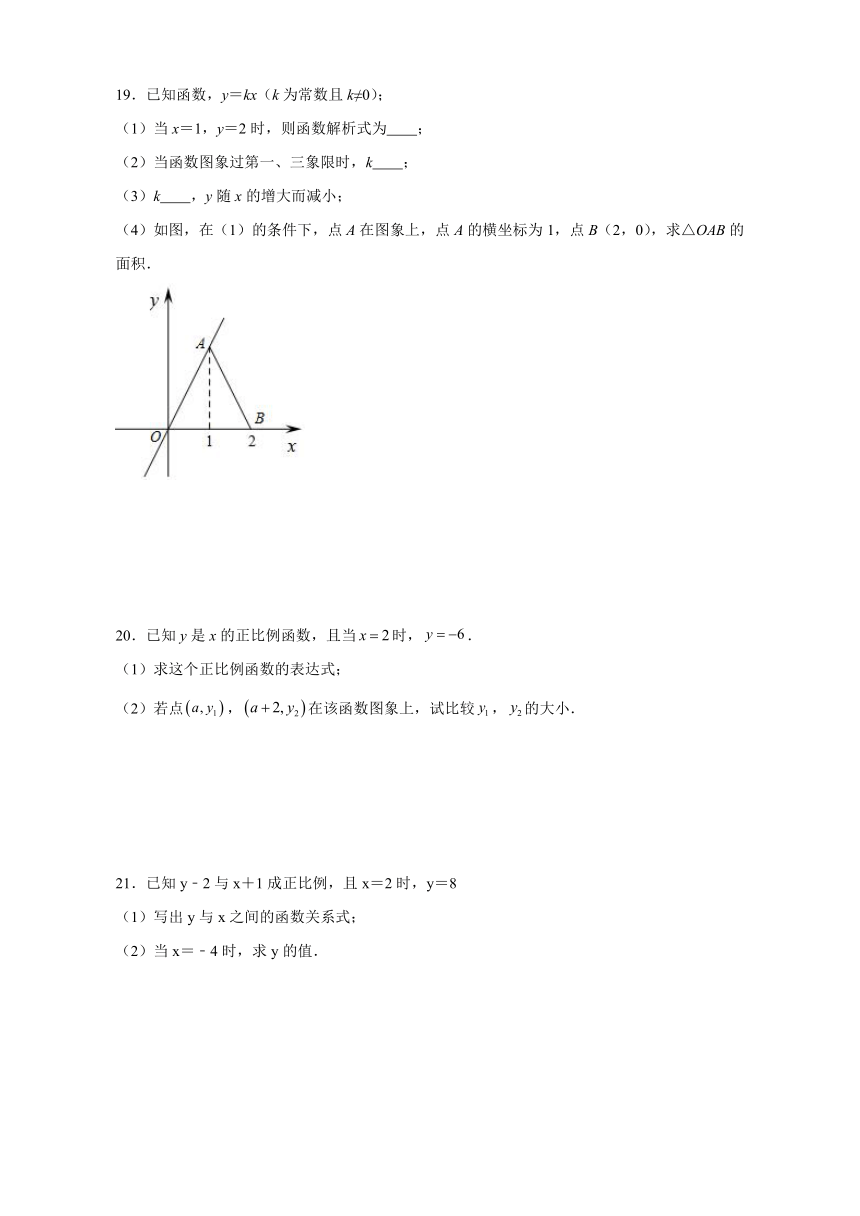
(4)如图,在(1)的条件下,点A在图象上,点A的横坐标为1,点B(2,0),求△OAB的面积.
20.已知y是x的正比例函数,且当时,.
(1)求这个正比例函数的表达式;
(2)若点,在该函数图象上,试比较,的大小.
21.已知y﹣2与x+1成正比例,且x=2时,y=8
(1)写出y与x之间的函数关系式;
(2)当x=﹣4时,求y的值.
参考答案
1.A
解:选项A:
y=80x,属于正比例函数,两个变量之间成正比例函数关系,符合题意;
选项B:属于二次函数,两个变量之间不是成正比例函数关系,不合题意;
选项C:
y=15+5x,
属于一次函数,两个变量之间不是成正比例函数关系,不合题意;
选项D:
S=6x2,属于二次函数,两个变量之间不是成正比例函数关系,不合题意;
故选:
A
2.B
解:A选项,y=x2,x次数为2,是2次函数,不符合题意.
B选项,y=,x次数为1,系数为,是正比例函数,符合题意.
C选项,y=,x次数为﹣1,是反比例函数,不符合题意.
D选项,y=2x+3为一次函数,不符合题意.
故选:B.
3.A
解:∵点A(-2,4)在正比例函数的图象上,
∴,解得k=-2.
故选:A.
4.A
解:把时,代入得,
2k=6,
k=3,
∴,
选项A,把x=-1代入得y=-3,即可得点在正比例函数的图象上,选项A符合题意;
选项B,把x=-1代入得y=-3,即可得点不在正比例函数的图象上,选项B不符合题意;
选项C,把x=1代入得y=3,即可得点不在正比例函数的图象上,选项C不符合题意;
选项D,把x=3代入得y=9,即可得点不在正比例函数的图象上,选项D不符合题意.
故选A.
5.C
解:设该正比例函数是y=kx(k≠0),则b=5k,4=ak.
∴=,
∴ab=20.
故选:C.
6.A
解:正比例函数中,,
此函数的图象经过一、三象限.
故选:A.
7.C
解:∵P1(x1,y1),P2(x2,y2)是正比例函数y=kx(k≠0)在第二象限的图象上的两个点,
∴k<0,
∴y随x的增大而减小,
∵P1点在P2点左边,
∴x1<x2,
∴y1>y2.
故选:C.
8.C
解:当正比例函数图象经过二、四象限,
可得,
故选:C.
9.B
解:∵正比例函数中,,
∴随的增大而增大,y没有最值.
故选B.
10.C
解:∵y=﹣x,
∴随的增大而减小
∴当x1<x2时,y1>y2
故答案选C.
11.D
解:因为正比例函数y=(a﹣1)x(a是常数)的图象在第一、三象限,
所以a﹣1>0,
解得:a>1,
故选:D.
12.D
解:由正比例函数y=(1﹣k)x.若函数值y随x的增大而减小,则有:
,
∴,
∴符合题意的只有D选项;
故选D.
13.-2
解:∵在y=3x﹣a﹣2中,
y是x的正比例函数,
∴
,
解得:
.
故答案为:-2.
14.
解:∵正比例函数y=kx的图象经过点(a,b),
∴b=ka,
又∵=2,
∴k==.
故答案为:.
15.3
解:∵正比例函数y=kx的图象经过点A(k,9),
∴k2=9,
∴k=±3,
∵函数图象经过第一、三象限,
∴k>0,
∴k=3,
故答案为3.
16.
解:∵正比例函数,的值随的值增大而减小
∴
∴.
故答案是:
17.m>
解:由题目分析可知:在正比例函数y=(1﹣2m)x中,y随x的增大而减小
由一次函数性质可知应有:1﹣2m<0,即﹣2m<﹣1,
解得:m>,
故答案为:.
18.(1)5;10;20;(2)y=10x
解:(1)由题意可得:
0.5×10=5元,1×10=10元,2×10=20元;
故答案为5;10;20;
(2)由(1)可设付款金额y与购买量x(x≥0)的函数表达式为y=kx,则有:
0.5k=5,解得:k=10,
∴付款金额y与购买量x(x≥0)的函数表达式为y=10x.
19.(1)y=2x;(2)>0;(3)<0;(4)2.
解:(1)当,时,,
,
故答案为;
(2)函数图象过第一、三象限,
,
故答案为;
(3)随的增大而减小,
函数图象经过第二、四象限,
,
故答案为;
(4),点的横坐标为1,
,
,
,
的面积.
20.(1)y=?3x;(2)>
解:(1)∵y与x成正比例,
∴设y=kx,
∵当时,.
∴-6=2k,
解得:k=?3,
∴y与x之间的函数表达式为:y=?3x;
(2)∵k=?3,
∴y随x的增大而减小,
∵点,在该函数图象上,a<a+2,
∴>.
21.(1)y=2x+4,(2)-4
解:(1)∵y﹣2与x+1成正比例,
∴设y﹣2=k(x+1)(k为常数,k≠0),
把x=2,y=8代入得:8﹣2=k(2+1),
解得:k=2,
即y﹣2=2(x+1),
即y=2x+4,
∴y与x之间的函数关系式是y=2x+4;
(2)当x=﹣4时,y=2×(﹣4)+4=﹣4.
一、单选题
1.下列问题中,两个变量之间是正比例函数关系的是(
)
A.汽车以的速度匀速行驶,行驶路程与行驶时间之间的关系
B.圆的面积与它的半径之间的关系
C.某水池有水,现打开进水管进水,进水速度,后水池有水
D.有一个边长为x的正方体,则它的表面积S与边长x之间的函数关系
2.下列函数中,是正比例函数的是( )
A.y=x2
B.y=
C.y=
D.y=2x+3
3.若点在正比例函数的图象上,则k的值为(
)
A.
B.2
C.
D.
4.若正比例函数,当时,,则下列各点在该函数图象上的是(
)
A.
B.
C.
D.
5.在平面直角坐标系中,若一个正比例函数的图象经过A(5,b),B(a,4)两点,则a,b一定满足的关系式为(
)
A.a﹣b=1
B.a+b=9
C.a?b=20
D.=
6.正比例函数的图象经过的象限是( )
A.第一、三象限
B.第二、四象限
C.第一、四象限
D.第二、三象限
7.已知P1(x1,y1),P2(x2,y2)是正比例函数y=kx(k≠0)在第二象限的图象上的两个点,如果P1点在P2点左边,那么y1,y2的大小关系是( )
A.y1=y2
B.y1<y2
C.y1>y2
D.不能确定
8.正比例函数的图像如图所示,下列说法正确的是(
)
A.
B.随的增大而增大
C.
D.函数图像经过点
9.对于正比例函数,下列说法正确的是(
)
A.随的增大而减小
B.随的增大而增大
C.随的减小而增大
D.有最小值
10.P1(x1,y1),P2(x2,y2)是正比例函数y=﹣x图象上的两点,则下列判断正确的是( )
A.y1>y2
B.y1<y2
C.当x1<x2时,y1>y2
D.当x1<x2时,y1<y2
11.如果正比例函数y=(a﹣1)x(a是常数)的图象在第一、三象限,那么a的取值范围是( )
A.a<0
B.a>0
C.a<1
D.a>1
12.已知正比例函数y=(1﹣k)x.若函数值y随x的增大而减小,则实数k的值可能是( )
A.﹣1
B.0
C.1
D.
二、填空题
13.在y=3x﹣a﹣2中,若y是x的正比例函数,则常数a=_____.
14.已知,正比例函数y=kx的图象经过点(a,b),且=2,则k的值等于_______________.
15.若正比例函数y=kx的图象经过点A(k,9),且经过第一、三象限,则k的值是
___.
16.已知正比例函数,的值随的值增大而减小,那么的取值范围是______.
17.若正比例函数y=(1﹣2m)x的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时,y1>y2,则m的取值范围是__________________.
三、解答题
18.永安批发市场某天鸡蛋的价格为10元/kg.
(1)填写下表;
购买量/kg
0.5
1
2
?
付款金额/元
?
(2)写出付款金额y与购买量x(x≥0)的函数表达式.
19.已知函数,y=kx(k为常数且k≠0);
(1)当x=1,y=2时,则函数解析式为 ;
(2)当函数图象过第一、三象限时,k ;
(3)k ,y随x的增大而减小;
(4)如图,在(1)的条件下,点A在图象上,点A的横坐标为1,点B(2,0),求△OAB的面积.
20.已知y是x的正比例函数,且当时,.
(1)求这个正比例函数的表达式;
(2)若点,在该函数图象上,试比较,的大小.
21.已知y﹣2与x+1成正比例,且x=2时,y=8
(1)写出y与x之间的函数关系式;
(2)当x=﹣4时,求y的值.
参考答案
1.A
解:选项A:
y=80x,属于正比例函数,两个变量之间成正比例函数关系,符合题意;
选项B:属于二次函数,两个变量之间不是成正比例函数关系,不合题意;
选项C:
y=15+5x,
属于一次函数,两个变量之间不是成正比例函数关系,不合题意;
选项D:
S=6x2,属于二次函数,两个变量之间不是成正比例函数关系,不合题意;
故选:
A
2.B
解:A选项,y=x2,x次数为2,是2次函数,不符合题意.
B选项,y=,x次数为1,系数为,是正比例函数,符合题意.
C选项,y=,x次数为﹣1,是反比例函数,不符合题意.
D选项,y=2x+3为一次函数,不符合题意.
故选:B.
3.A
解:∵点A(-2,4)在正比例函数的图象上,
∴,解得k=-2.
故选:A.
4.A
解:把时,代入得,
2k=6,
k=3,
∴,
选项A,把x=-1代入得y=-3,即可得点在正比例函数的图象上,选项A符合题意;
选项B,把x=-1代入得y=-3,即可得点不在正比例函数的图象上,选项B不符合题意;
选项C,把x=1代入得y=3,即可得点不在正比例函数的图象上,选项C不符合题意;
选项D,把x=3代入得y=9,即可得点不在正比例函数的图象上,选项D不符合题意.
故选A.
5.C
解:设该正比例函数是y=kx(k≠0),则b=5k,4=ak.
∴=,
∴ab=20.
故选:C.
6.A
解:正比例函数中,,
此函数的图象经过一、三象限.
故选:A.
7.C
解:∵P1(x1,y1),P2(x2,y2)是正比例函数y=kx(k≠0)在第二象限的图象上的两个点,
∴k<0,
∴y随x的增大而减小,
∵P1点在P2点左边,
∴x1<x2,
∴y1>y2.
故选:C.
8.C
解:当正比例函数图象经过二、四象限,
可得,
故选:C.
9.B
解:∵正比例函数中,,
∴随的增大而增大,y没有最值.
故选B.
10.C
解:∵y=﹣x,
∴随的增大而减小
∴当x1<x2时,y1>y2
故答案选C.
11.D
解:因为正比例函数y=(a﹣1)x(a是常数)的图象在第一、三象限,
所以a﹣1>0,
解得:a>1,
故选:D.
12.D
解:由正比例函数y=(1﹣k)x.若函数值y随x的增大而减小,则有:
,
∴,
∴符合题意的只有D选项;
故选D.
13.-2
解:∵在y=3x﹣a﹣2中,
y是x的正比例函数,
∴
,
解得:
.
故答案为:-2.
14.
解:∵正比例函数y=kx的图象经过点(a,b),
∴b=ka,
又∵=2,
∴k==.
故答案为:.
15.3
解:∵正比例函数y=kx的图象经过点A(k,9),
∴k2=9,
∴k=±3,
∵函数图象经过第一、三象限,
∴k>0,
∴k=3,
故答案为3.
16.
解:∵正比例函数,的值随的值增大而减小
∴
∴.
故答案是:
17.m>
解:由题目分析可知:在正比例函数y=(1﹣2m)x中,y随x的增大而减小
由一次函数性质可知应有:1﹣2m<0,即﹣2m<﹣1,
解得:m>,
故答案为:.
18.(1)5;10;20;(2)y=10x
解:(1)由题意可得:
0.5×10=5元,1×10=10元,2×10=20元;
故答案为5;10;20;
(2)由(1)可设付款金额y与购买量x(x≥0)的函数表达式为y=kx,则有:
0.5k=5,解得:k=10,
∴付款金额y与购买量x(x≥0)的函数表达式为y=10x.
19.(1)y=2x;(2)>0;(3)<0;(4)2.
解:(1)当,时,,
,
故答案为;
(2)函数图象过第一、三象限,
,
故答案为;
(3)随的增大而减小,
函数图象经过第二、四象限,
,
故答案为;
(4),点的横坐标为1,
,
,
,
的面积.
20.(1)y=?3x;(2)>
解:(1)∵y与x成正比例,
∴设y=kx,
∵当时,.
∴-6=2k,
解得:k=?3,
∴y与x之间的函数表达式为:y=?3x;
(2)∵k=?3,
∴y随x的增大而减小,
∵点,在该函数图象上,a<a+2,
∴>.
21.(1)y=2x+4,(2)-4
解:(1)∵y﹣2与x+1成正比例,
∴设y﹣2=k(x+1)(k为常数,k≠0),
把x=2,y=8代入得:8﹣2=k(2+1),
解得:k=2,
即y﹣2=2(x+1),
即y=2x+4,
∴y与x之间的函数关系式是y=2x+4;
(2)当x=﹣4时,y=2×(﹣4)+4=﹣4.
