2021-2022学年人教版九年级数学上册21.3实际问题与一元二次方程(1)同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册21.3实际问题与一元二次方程(1)同步练习(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 325.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 11:30:44 | ||
图片预览




文档简介
2021-2022学年九年级数学上册同步(人教版)
21.3实际问题与一元二次方程(1)
时间:60分钟
一、单选题
1.某农家前年水蜜桃亩产量为800千克,今年的亩产量为1200千克.设从前年到今年平均增长率都为x,则可列方程( )
A.800(1+2x)=1200
B.800(1+x2)=1200
C.800(1+x)2=1200
D.800(1+x)=1200
2.某经济开发区,今年一月份工业产值达50亿元,第一季度总产值为175亿元,二月、三月平均每月的增长率是多少?若设平均每月的增长率为x,根据题意,可列方程为( )
A.50(1+x)2=175
B.50+50(1+x)+50(1+x)2=175
C.50(1+x)+50(1+x)2=175
D.50+50(1+x)2=175
3.元旦当天,小明将收到的一条微信,发送给若干人,每个收到微信的人又给相同数量的人转发了这条微信,此时收到这条微信的人共有157人,则小明给多少人发了微信(
)
A.10
B.11
C.12
D.13
4.爷爷的生日晚宴上,大家两两碰杯一次,总共碰杯45次,那么有几人参加了这次宴会?(
)
A.8人
B.9人
C.10人
D.11人
5.已知一个两位数,个位上的数字比十位上的数字少4,这个两位数十位和个位交换位置后,新两位数与原两位数的积为1612,那么原两位数是(
)
A.95
B.59
C.26
D.62
6.某数的一半比这个数的平方的3倍少,设某数为x,某数的方程是(
)
A.
B.
C.
D.
7.如图,要设计一幅宽、长的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为,如果要使所有彩条所占面积为原矩形图案面积的三分之一,则横彩条和竖彩条的宽度分别是(
)
A.和
B.和
C.和
D.和
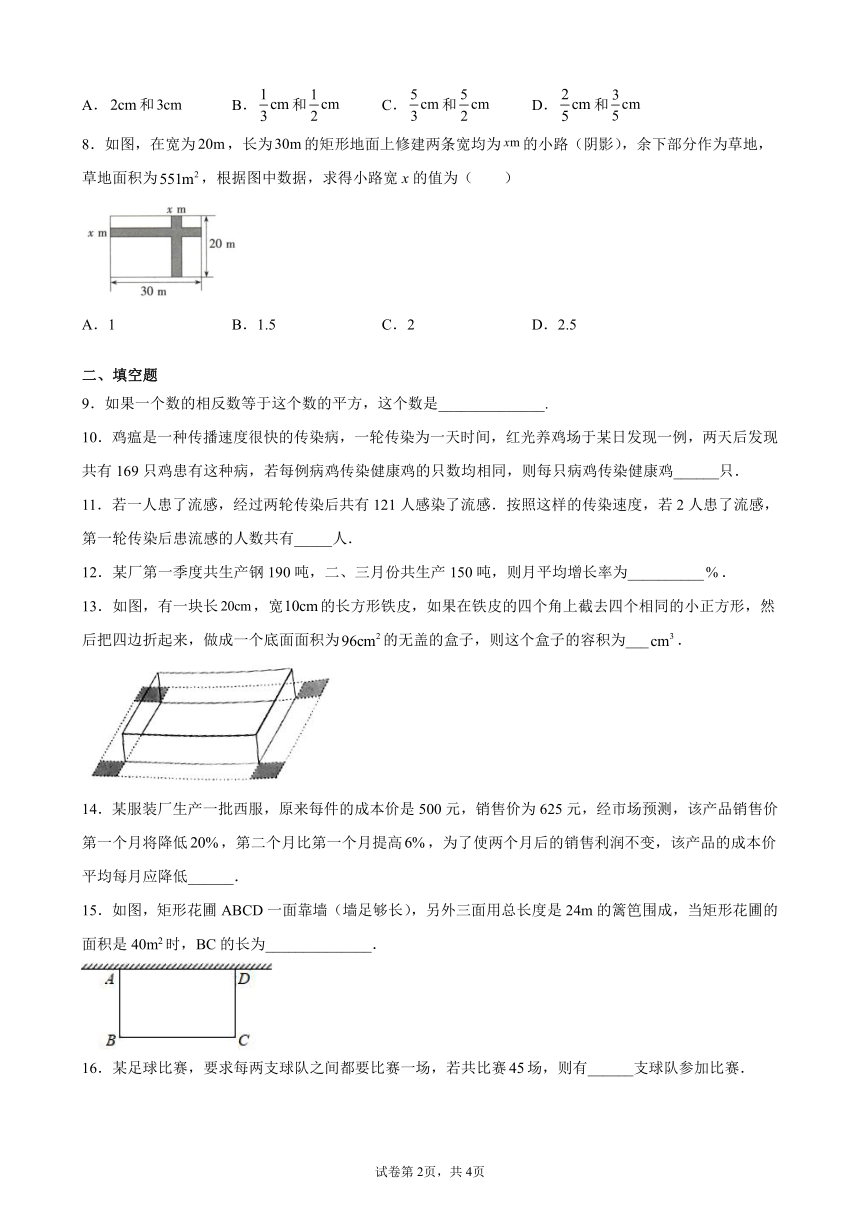
8.如图,在宽为,长为的矩形地面上修建两条宽均为的小路(阴影),余下部分作为草地,草地面积为,根据图中数据,求得小路宽x的值为(
)
A.1
B.1.5
C.2
D.2.5
二、填空题
9.如果一个数的相反数等于这个数的平方,这个数是______________.
10.鸡瘟是一种传播速度很快的传染病,一轮传染为一天时间,红光养鸡场于某日发现一例,两天后发现共有169只鸡患有这种病,若每例病鸡传染健康鸡的只数均相同,则每只病鸡传染健康鸡______只.
11.若一人患了流感,经过两轮传染后共有121人感染了流感.按照这样的传染速度,若2人患了流感,第一轮传染后患流感的人数共有_____人.
12.某厂第一季度共生产钢190吨,二、三月份共生产150吨,则月平均增长率为__________.
13.如图,有一块长,宽的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为的无盖的盒子,则这个盒子的容积为___.
14.某服装厂生产一批西服,原来每件的成本价是500元,销售价为625元,经市场预测,该产品销售价第一个月将降低,第二个月比第一个月提高,为了使两个月后的销售利润不变,该产品的成本价平均每月应降低______.
15.如图,矩形花圃ABCD一面靠墙(墙足够长),另外三面用总长度是24m的篱笆围成,当矩形花圃的面积是40m2时,BC的长为______________.
16.某足球比赛,要求每两支球队之间都要比赛一场,若共比赛场,则有______支球队参加比赛.
三、解答题
17.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
18.一个两位数,两个数字的和为5,把这个两位数的个位上的数字与十位上的数字互换得到一个新的两位数,它与原两位数的积为736,求原两位数.
19.子曰:“吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩.”—《论语·第十二章·为政篇》
列方程解决下面问题:
大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符
哪位学子算得快,多少年华属周瑜?
20.如图,矩形是景区内一块油菜花地,,,点E、F、G、H分别在矩形的四条边上,且,现在其中修建一条观花道(阴影所示)供游人赏花.若观花道的面积为,求的长.
21.某农场去年种植南瓜10亩,总产量为,今年该农场扩大了种植面积,并引进新品种,使产量增长到.已知今年种植面积的增长率是今年平均亩产量增长率的2倍,求今年平均亩产量的增长率.
22.某象棋比赛,每名选手都要与其他选手比赛一局,每局胜者记2分,负者记0分,和棋各记1分.有四位观众统计了比赛中全部选手得分总数,分别是2017,2070,2018,2078,经核实,只有一位观众统计准确,则这次比赛的选手共有多少名?
23.根据下列问题,设出未知数x,列出关于x的方程,并将其化为一元二次方程的一般形式.
(1)有一个三位数,它的个位数字比十位数字大3,十位数字比百位数字小2,三个数字的平方和的9倍比这个三位数大20,求这个三位数;
(2)如果一个直角三角形的两条直角边长之和为,面积为,求它的两条直角边的长.
24.某种农产品今年第一季度价格大幅度下降,下降后每千克的价格是原价格的,下降后,用60元买这种农产品比原来多买了2千克.
(1)求该种农产品下降后的价格;
(2)从第二季度开始,该种农产品的价格开始回升,经过两个季度,该种农产品的价格上升到每千克14.4元.求第二和第三季度该种农产品价格的平均增长率.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:去年水蜜桃的亩产量为800×(1+x),今年水蜜桃的亩产量在去年水蜜桃的亩产量的基础上增加x,
为800×(1+x)×(1+x),则列出的方程是800(1+x)2=1200,
故选C.
2.B
【解析】解:二月份的产值为:50(1+x),
三月份的产值为:50(1+x)(1+x)=50(1+x)2,
故第一季度总产值为:50+50(1+x)+50(1+x)2=175.
故选:B.
3.C
【解析】解:设小明发短信给x个人,由题意得:
∴1+x+x2=157,
解得:x1=12,x2=-13(不合题意舍去),
答:小明发短信给12个人,
故选:C.
4.C
【解析】解:设有x人参加了这次宴会,根据题意列方程得,
,
解得x?=10,x?=?9(不合题意,舍去),
∴有10人参加了这次宴会.
故选:C.
5.D
【解析】解:令个位为y,十位为x,则数为10x+y,且x-4=y,交换位置后,数字为10y+x,则
(10x+y)×(10y+x)=1612,即(11x-4)×(11x-40)=1612,
解得x=6,
10x+y=60+(6-4)=62.
故这个两位数是62.
故选:D.
6.D
【解析】由已知得:的一半为,的平方的倍为,
则有:.
故选:D.
7.C
【解析】解:设横彩条的宽度为,则竖彩条的宽度为,
由图可知一个横彩条的面积为:,一个竖彩条的面积为:,
有四个重叠的部分,重叠的面积为:,
因为所有彩条的面积为总面积的三分之一,
所以列方程为:
,
解得:,(不符合题意,舍去),
∴,
应设计横的彩条宽为,竖的彩条宽为.
故选:.
8.A
【解析】解:根据题意,得,
整理,得,
解得,
∵当时,,
∴舍去,
∴小路宽x的值为1.
故选A.
9.0或-1.
【解析】解:设这个数为x,
-x
=
x2
x(x+1)=0,
解得x1=0,x2=-1,
故答案为:0或-1.
10.12
【解析】解:设每只病鸡传染健康鸡x只,由题意得:
x+1+x(x+1)=169,
整理,得,
解得(不符合题意舍去).
答:设每只病鸡传染健康鸡12只.
故答案为:12.
11.22
【解析】解:设每轮传染中1人传染给x人,则第一轮传染后共(1+x)人患流感,第二轮传染后共[1+x+x(x+1)]人患流感,
根据题意得:1+x+x(x+1)=121,
解得:x1=10,x2=﹣12(舍去),
∴2(1+x)=22.
故答案为22.
12.50
【解析】设月平均增长率为x,
依题意可知一月份产量为(吨),
则
,解得,(舍去),
故答案为:.
13.192
【解析】解:设截去的四个相同的小正方形边长为,
则无盖盒子的底面长为,宽为,
由题意:,
解得:或(不合题意,舍去),
∴小正方形边长为2,
则该无盖盒子的高为2,
∴其容积为:,
故答案为:192.
14.
【解析】设该产品的成本价平均每月降低率为x,
根据题意,得,
整理得,
解得(舍去),.
∴该产品的成本价平均每月应降低.
故答案为:10%.
15.4m或20m.
【解析】设BC的长度为xm,
由题意得
x?=40,
整理得:x2﹣24x+80=0,即(x﹣4)(x﹣20)=0,
解得
x1=4,x2=20,
答:BC长为4m或20m.
故答案为:4m或20m.
16.10
【解析】∵有x支球队参加篮球比赛,每两队之间都比赛一场,
∴共比赛场数为x(x-1),
∴共比赛了45场,
∴x(x-1)=45,
解得:x1=10,x2=-9(舍去),
故答案为:10.
17.每轮感染中平均1台电脑会感染8台电脑,3轮感染后被感染的电脑会超过700台.
【解析】设每轮感染中平均1台电脑会感染台电脑.
根据题意可列:,
解得:,(舍去).
∴3轮感染后,被感染得电脑为:.
答:每轮感染中平均1台电脑会感染8台电脑,3轮感染后被感染的电脑会超过700台.
18.23或32.
【解析】解:设原两位数字的十位数字为x,则个位数字为(5-x),
根据题意得(10x+5-x)[10(5-x)+x]=736,
整理得:x2-5x+6=0,
解得:x1=2,x2=3,
∴5-x=3或2,
∴原两位数是23或32.
故答案为:23或32.
19.周瑜的年龄是36岁.
【解析】解:设周瑜逝世的年龄的个位数字为x,则十位数字为x-3,
根据题意得:10(x-3)+x=x2,
解得:x1=5,x2=6,
当x1=5时,周瑜的年龄是25岁,
∵25非而立之年,
∴不符合题意,舍去;
当x2=6时,周瑜的年龄是36岁,符合题意.
答:周瑜的年龄是36岁.
20.
【解析】解:设,则,,
根据题意,得,整理得:,
解得:.
∵,∴,∴.
答:的长为.
21.今年平均亩产量的增长率为.
【解析】解:设今年平均亩产量的增长率为x,则今年种植面积的平均增长率为.
根据题意,得.
解得,(不合题意,舍去).
答:今年平均亩产量的增长率为.
22.这次比赛的选手共有46名.
【解析】解:设这次比赛共有x名选手.
由题意可知,无论胜负,每局两名选手得分总和均为2分,x名选手比赛的总局数为,
所以得分总数为.
因为x是正整数,且大于1,所以x,是两个连续的正整数.
不难验证:两个连续的整数之积的末位数字只能是0,2,6,故得分总数只能是2070,
则,
解得(舍去).
答:这次比赛的选手共有46名.
23.(1),;(2),.
【解析】解:(1)设十位数字为x,则个位数字为,百位数字为,根据题意得:,
化简为;
(2)设其中一条直角边的长为,则另一条直角边的长为,
根据题意得,
整理得.
24.(1)10元;(2)20%
【解析】解:(1)设该种农产品的原价格是元/千克,则下降后的价格是元/千克,
根据题意,得,解得,
经检验:是原方程的解,
故,
答:该种农产品下降后的价格是每千克10元.
(2)设第二和第三季度该种农产品价格的平均增长率是,
根据题意,得,
解得或(不合题意,舍去)
答:第二和第三季度该种农产品价格的平均增长率是20%.
答案第1页,共2页
答案第1页,共2页
21.3实际问题与一元二次方程(1)
时间:60分钟
一、单选题
1.某农家前年水蜜桃亩产量为800千克,今年的亩产量为1200千克.设从前年到今年平均增长率都为x,则可列方程( )
A.800(1+2x)=1200
B.800(1+x2)=1200
C.800(1+x)2=1200
D.800(1+x)=1200
2.某经济开发区,今年一月份工业产值达50亿元,第一季度总产值为175亿元,二月、三月平均每月的增长率是多少?若设平均每月的增长率为x,根据题意,可列方程为( )
A.50(1+x)2=175
B.50+50(1+x)+50(1+x)2=175
C.50(1+x)+50(1+x)2=175
D.50+50(1+x)2=175
3.元旦当天,小明将收到的一条微信,发送给若干人,每个收到微信的人又给相同数量的人转发了这条微信,此时收到这条微信的人共有157人,则小明给多少人发了微信(
)
A.10
B.11
C.12
D.13
4.爷爷的生日晚宴上,大家两两碰杯一次,总共碰杯45次,那么有几人参加了这次宴会?(
)
A.8人
B.9人
C.10人
D.11人
5.已知一个两位数,个位上的数字比十位上的数字少4,这个两位数十位和个位交换位置后,新两位数与原两位数的积为1612,那么原两位数是(
)
A.95
B.59
C.26
D.62
6.某数的一半比这个数的平方的3倍少,设某数为x,某数的方程是(
)
A.
B.
C.
D.
7.如图,要设计一幅宽、长的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为,如果要使所有彩条所占面积为原矩形图案面积的三分之一,则横彩条和竖彩条的宽度分别是(
)
A.和
B.和
C.和
D.和
8.如图,在宽为,长为的矩形地面上修建两条宽均为的小路(阴影),余下部分作为草地,草地面积为,根据图中数据,求得小路宽x的值为(
)
A.1
B.1.5
C.2
D.2.5
二、填空题
9.如果一个数的相反数等于这个数的平方,这个数是______________.
10.鸡瘟是一种传播速度很快的传染病,一轮传染为一天时间,红光养鸡场于某日发现一例,两天后发现共有169只鸡患有这种病,若每例病鸡传染健康鸡的只数均相同,则每只病鸡传染健康鸡______只.
11.若一人患了流感,经过两轮传染后共有121人感染了流感.按照这样的传染速度,若2人患了流感,第一轮传染后患流感的人数共有_____人.
12.某厂第一季度共生产钢190吨,二、三月份共生产150吨,则月平均增长率为__________.
13.如图,有一块长,宽的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为的无盖的盒子,则这个盒子的容积为___.
14.某服装厂生产一批西服,原来每件的成本价是500元,销售价为625元,经市场预测,该产品销售价第一个月将降低,第二个月比第一个月提高,为了使两个月后的销售利润不变,该产品的成本价平均每月应降低______.
15.如图,矩形花圃ABCD一面靠墙(墙足够长),另外三面用总长度是24m的篱笆围成,当矩形花圃的面积是40m2时,BC的长为______________.
16.某足球比赛,要求每两支球队之间都要比赛一场,若共比赛场,则有______支球队参加比赛.
三、解答题
17.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
18.一个两位数,两个数字的和为5,把这个两位数的个位上的数字与十位上的数字互换得到一个新的两位数,它与原两位数的积为736,求原两位数.
19.子曰:“吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩.”—《论语·第十二章·为政篇》
列方程解决下面问题:
大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符
哪位学子算得快,多少年华属周瑜?
20.如图,矩形是景区内一块油菜花地,,,点E、F、G、H分别在矩形的四条边上,且,现在其中修建一条观花道(阴影所示)供游人赏花.若观花道的面积为,求的长.
21.某农场去年种植南瓜10亩,总产量为,今年该农场扩大了种植面积,并引进新品种,使产量增长到.已知今年种植面积的增长率是今年平均亩产量增长率的2倍,求今年平均亩产量的增长率.
22.某象棋比赛,每名选手都要与其他选手比赛一局,每局胜者记2分,负者记0分,和棋各记1分.有四位观众统计了比赛中全部选手得分总数,分别是2017,2070,2018,2078,经核实,只有一位观众统计准确,则这次比赛的选手共有多少名?
23.根据下列问题,设出未知数x,列出关于x的方程,并将其化为一元二次方程的一般形式.
(1)有一个三位数,它的个位数字比十位数字大3,十位数字比百位数字小2,三个数字的平方和的9倍比这个三位数大20,求这个三位数;
(2)如果一个直角三角形的两条直角边长之和为,面积为,求它的两条直角边的长.
24.某种农产品今年第一季度价格大幅度下降,下降后每千克的价格是原价格的,下降后,用60元买这种农产品比原来多买了2千克.
(1)求该种农产品下降后的价格;
(2)从第二季度开始,该种农产品的价格开始回升,经过两个季度,该种农产品的价格上升到每千克14.4元.求第二和第三季度该种农产品价格的平均增长率.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:去年水蜜桃的亩产量为800×(1+x),今年水蜜桃的亩产量在去年水蜜桃的亩产量的基础上增加x,
为800×(1+x)×(1+x),则列出的方程是800(1+x)2=1200,
故选C.
2.B
【解析】解:二月份的产值为:50(1+x),
三月份的产值为:50(1+x)(1+x)=50(1+x)2,
故第一季度总产值为:50+50(1+x)+50(1+x)2=175.
故选:B.
3.C
【解析】解:设小明发短信给x个人,由题意得:
∴1+x+x2=157,
解得:x1=12,x2=-13(不合题意舍去),
答:小明发短信给12个人,
故选:C.
4.C
【解析】解:设有x人参加了这次宴会,根据题意列方程得,
,
解得x?=10,x?=?9(不合题意,舍去),
∴有10人参加了这次宴会.
故选:C.
5.D
【解析】解:令个位为y,十位为x,则数为10x+y,且x-4=y,交换位置后,数字为10y+x,则
(10x+y)×(10y+x)=1612,即(11x-4)×(11x-40)=1612,
解得x=6,
10x+y=60+(6-4)=62.
故这个两位数是62.
故选:D.
6.D
【解析】由已知得:的一半为,的平方的倍为,
则有:.
故选:D.
7.C
【解析】解:设横彩条的宽度为,则竖彩条的宽度为,
由图可知一个横彩条的面积为:,一个竖彩条的面积为:,
有四个重叠的部分,重叠的面积为:,
因为所有彩条的面积为总面积的三分之一,
所以列方程为:
,
解得:,(不符合题意,舍去),
∴,
应设计横的彩条宽为,竖的彩条宽为.
故选:.
8.A
【解析】解:根据题意,得,
整理,得,
解得,
∵当时,,
∴舍去,
∴小路宽x的值为1.
故选A.
9.0或-1.
【解析】解:设这个数为x,
-x
=
x2
x(x+1)=0,
解得x1=0,x2=-1,
故答案为:0或-1.
10.12
【解析】解:设每只病鸡传染健康鸡x只,由题意得:
x+1+x(x+1)=169,
整理,得,
解得(不符合题意舍去).
答:设每只病鸡传染健康鸡12只.
故答案为:12.
11.22
【解析】解:设每轮传染中1人传染给x人,则第一轮传染后共(1+x)人患流感,第二轮传染后共[1+x+x(x+1)]人患流感,
根据题意得:1+x+x(x+1)=121,
解得:x1=10,x2=﹣12(舍去),
∴2(1+x)=22.
故答案为22.
12.50
【解析】设月平均增长率为x,
依题意可知一月份产量为(吨),
则
,解得,(舍去),
故答案为:.
13.192
【解析】解:设截去的四个相同的小正方形边长为,
则无盖盒子的底面长为,宽为,
由题意:,
解得:或(不合题意,舍去),
∴小正方形边长为2,
则该无盖盒子的高为2,
∴其容积为:,
故答案为:192.
14.
【解析】设该产品的成本价平均每月降低率为x,
根据题意,得,
整理得,
解得(舍去),.
∴该产品的成本价平均每月应降低.
故答案为:10%.
15.4m或20m.
【解析】设BC的长度为xm,
由题意得
x?=40,
整理得:x2﹣24x+80=0,即(x﹣4)(x﹣20)=0,
解得
x1=4,x2=20,
答:BC长为4m或20m.
故答案为:4m或20m.
16.10
【解析】∵有x支球队参加篮球比赛,每两队之间都比赛一场,
∴共比赛场数为x(x-1),
∴共比赛了45场,
∴x(x-1)=45,
解得:x1=10,x2=-9(舍去),
故答案为:10.
17.每轮感染中平均1台电脑会感染8台电脑,3轮感染后被感染的电脑会超过700台.
【解析】设每轮感染中平均1台电脑会感染台电脑.
根据题意可列:,
解得:,(舍去).
∴3轮感染后,被感染得电脑为:.
答:每轮感染中平均1台电脑会感染8台电脑,3轮感染后被感染的电脑会超过700台.
18.23或32.
【解析】解:设原两位数字的十位数字为x,则个位数字为(5-x),
根据题意得(10x+5-x)[10(5-x)+x]=736,
整理得:x2-5x+6=0,
解得:x1=2,x2=3,
∴5-x=3或2,
∴原两位数是23或32.
故答案为:23或32.
19.周瑜的年龄是36岁.
【解析】解:设周瑜逝世的年龄的个位数字为x,则十位数字为x-3,
根据题意得:10(x-3)+x=x2,
解得:x1=5,x2=6,
当x1=5时,周瑜的年龄是25岁,
∵25非而立之年,
∴不符合题意,舍去;
当x2=6时,周瑜的年龄是36岁,符合题意.
答:周瑜的年龄是36岁.
20.
【解析】解:设,则,,
根据题意,得,整理得:,
解得:.
∵,∴,∴.
答:的长为.
21.今年平均亩产量的增长率为.
【解析】解:设今年平均亩产量的增长率为x,则今年种植面积的平均增长率为.
根据题意,得.
解得,(不合题意,舍去).
答:今年平均亩产量的增长率为.
22.这次比赛的选手共有46名.
【解析】解:设这次比赛共有x名选手.
由题意可知,无论胜负,每局两名选手得分总和均为2分,x名选手比赛的总局数为,
所以得分总数为.
因为x是正整数,且大于1,所以x,是两个连续的正整数.
不难验证:两个连续的整数之积的末位数字只能是0,2,6,故得分总数只能是2070,
则,
解得(舍去).
答:这次比赛的选手共有46名.
23.(1),;(2),.
【解析】解:(1)设十位数字为x,则个位数字为,百位数字为,根据题意得:,
化简为;
(2)设其中一条直角边的长为,则另一条直角边的长为,
根据题意得,
整理得.
24.(1)10元;(2)20%
【解析】解:(1)设该种农产品的原价格是元/千克,则下降后的价格是元/千克,
根据题意,得,解得,
经检验:是原方程的解,
故,
答:该种农产品下降后的价格是每千克10元.
(2)设第二和第三季度该种农产品价格的平均增长率是,
根据题意,得,
解得或(不合题意,舍去)
答:第二和第三季度该种农产品价格的平均增长率是20%.
答案第1页,共2页
答案第1页,共2页
同课章节目录
