3.2.1双曲线及其标准方程-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第一册课件(共20张PPT)
文档属性
| 名称 | 3.2.1双曲线及其标准方程-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第一册课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 540.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 14:57:48 | ||
图片预览







文档简介
(共20张PPT)
第三章
圆锥曲线的方程
3.2.1双曲线及其标准方程
复习引入
标准方程
图象
范围
对称性
顶点坐标
焦点坐标
半轴长
焦距
a,b,c关系
离心率
|x|≤
a,|y|≤
b
|x|≤
b,|y|≤
a
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,短半轴长为b.
焦距为2c;
a2=b2+c2
(a,0)、(-a,0)、(0,b)、(0,-b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(c,0)、(-c,0)
(0
,
c)、(0,
-c)
(01.
椭圆的定义:
和
等于常数
2a
(
2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2.
思考:
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
课堂探究
课堂探究
平面内与两个定点F1,F2的距离的差的绝对值
等于非零常数
的点的轨迹叫做
双曲线.
(小于︱F1F2︱)
2
F
F
1
M
课堂探究
①
两个定点F1、F2——双曲线的焦点;
②
|F1F2|=2c
——焦距.
没有“绝对值”这个条件时,仅表示双曲线的一支.
③此常数记为2a,则a2
F
F
1
M
课堂探究
双曲线的一支
两条射线
1、平面内与两定点F1,F2的距离的差等于非零常数2a
(小于|F1F2
|)的点的轨迹是什么?
2、若常数2a=0,轨迹是什么?
线段F1F2的垂直平分线
4、若常数2a>|F1F2|轨迹是什么?
轨迹不存在
3、若常数2a=|F1F2|轨迹是什么?
课堂探究
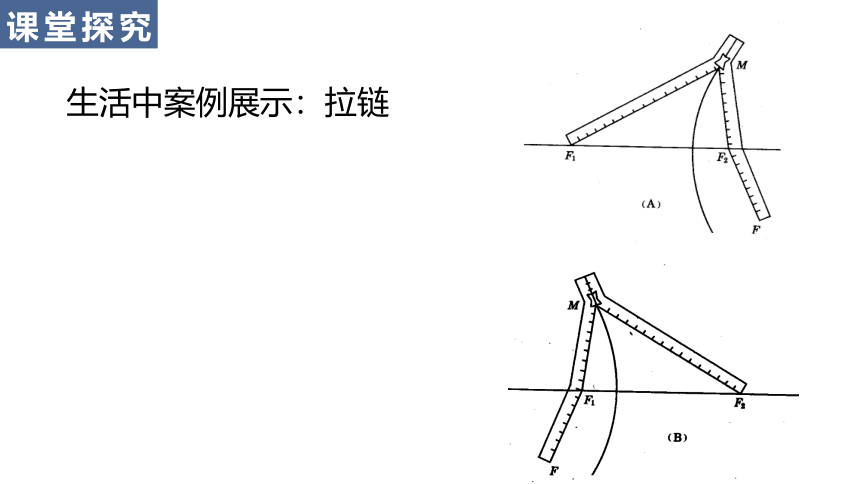
生活中案例展示:拉链
课堂探究
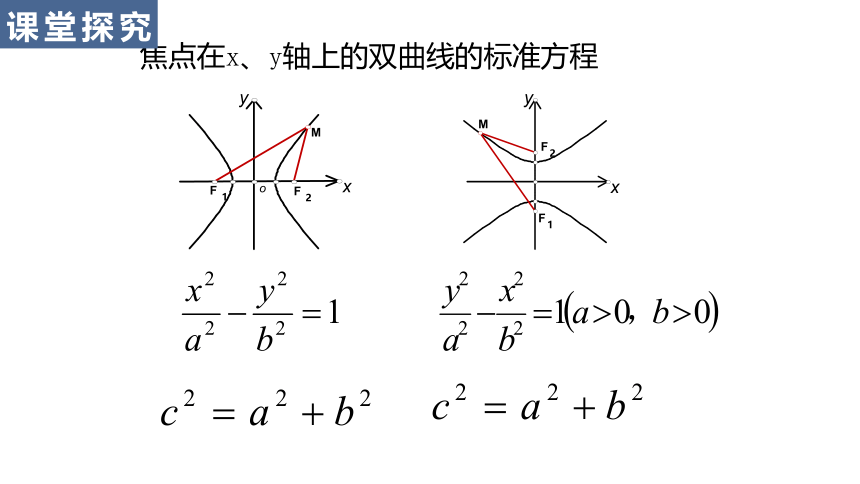
焦点在x、y轴上的双曲线的标准方程
课堂探究
1.用正负确定焦点位置(与分母大小无关)
2.a、b大小不定
3.c2=a2+b2
特别:当焦点位置不确定,可设方程为
mx2+ny2=1(mn<0).
课堂探究
例1:已知下列双曲线的方程:
3
4
5
(0,-5),(0,5)
1
2
(-2,0),(2,0)
(3)a=4,b=3,焦点在x轴上,求双曲线方程;
例题解析
解:因为双曲线焦点在y轴上,
可设其方程为
由双曲线得定义可知c=6
所以a=
所以b2=c2-a2=36-20=16
故双曲线得标准方程为
例2:求满足条件的双曲线的标准方程,已知焦点为
F1(0,-6),F2(0,6),过点M(2,-5)
例题解析
.
解:双曲线的方程为mx2+ny2=1(mn<0)
∵点A、B在椭圆上
所以
所以双曲线的方程为
故双曲线得标准方程为
例3:求满足条件的双曲线的标准方程,已知
例题解析
例题解析
例题解析
1.如果方程
表示双曲线,求m的取值范围.
解:
练习巩固
2.方程
表示焦点在y轴双曲线时,
则m的取值范围_____________.
练习巩固
练习巩固
你学到了什么?
课堂小结
作业1:书本
练习
作业2:
名师基础部分
作业3:
报纸第
期
版
作业布置
第三章
圆锥曲线的方程
3.2.1双曲线及其标准方程
复习引入
标准方程
图象
范围
对称性
顶点坐标
焦点坐标
半轴长
焦距
a,b,c关系
离心率
|x|≤
a,|y|≤
b
|x|≤
b,|y|≤
a
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,短半轴长为b.
焦距为2c;
a2=b2+c2
(a,0)、(-a,0)、(0,b)、(0,-b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(c,0)、(-c,0)
(0
,
c)、(0,
-c)
(0
椭圆的定义:
和
等于常数
2a
(
2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2.
思考:
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
课堂探究
课堂探究
平面内与两个定点F1,F2的距离的差的绝对值
等于非零常数
的点的轨迹叫做
双曲线.
(小于︱F1F2︱)
2
F
F
1
M
课堂探究
①
两个定点F1、F2——双曲线的焦点;
②
|F1F2|=2c
——焦距.
没有“绝对值”这个条件时,仅表示双曲线的一支.
③此常数记为2a,则a
F
F
1
M
课堂探究
双曲线的一支
两条射线
1、平面内与两定点F1,F2的距离的差等于非零常数2a
(小于|F1F2
|)的点的轨迹是什么?
2、若常数2a=0,轨迹是什么?
线段F1F2的垂直平分线
4、若常数2a>|F1F2|轨迹是什么?
轨迹不存在
3、若常数2a=|F1F2|轨迹是什么?
课堂探究
生活中案例展示:拉链
课堂探究
焦点在x、y轴上的双曲线的标准方程
课堂探究
1.用正负确定焦点位置(与分母大小无关)
2.a、b大小不定
3.c2=a2+b2
特别:当焦点位置不确定,可设方程为
mx2+ny2=1(mn<0).
课堂探究
例1:已知下列双曲线的方程:
3
4
5
(0,-5),(0,5)
1
2
(-2,0),(2,0)
(3)a=4,b=3,焦点在x轴上,求双曲线方程;
例题解析
解:因为双曲线焦点在y轴上,
可设其方程为
由双曲线得定义可知c=6
所以a=
所以b2=c2-a2=36-20=16
故双曲线得标准方程为
例2:求满足条件的双曲线的标准方程,已知焦点为
F1(0,-6),F2(0,6),过点M(2,-5)
例题解析
.
解:双曲线的方程为mx2+ny2=1(mn<0)
∵点A、B在椭圆上
所以
所以双曲线的方程为
故双曲线得标准方程为
例3:求满足条件的双曲线的标准方程,已知
例题解析
例题解析
例题解析
1.如果方程
表示双曲线,求m的取值范围.
解:
练习巩固
2.方程
表示焦点在y轴双曲线时,
则m的取值范围_____________.
练习巩固
练习巩固
你学到了什么?
课堂小结
作业1:书本
练习
作业2:
名师基础部分
作业3:
报纸第
期
版
作业布置
