第17章 勾股定理 章末小结 课件(共31张PPT)
文档属性
| 名称 | 第17章 勾股定理 章末小结 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 06:24:55 | ||
图片预览










文档简介
(共31张PPT)
第十七章
勾股定理
章末小结
人教版
八年级下册
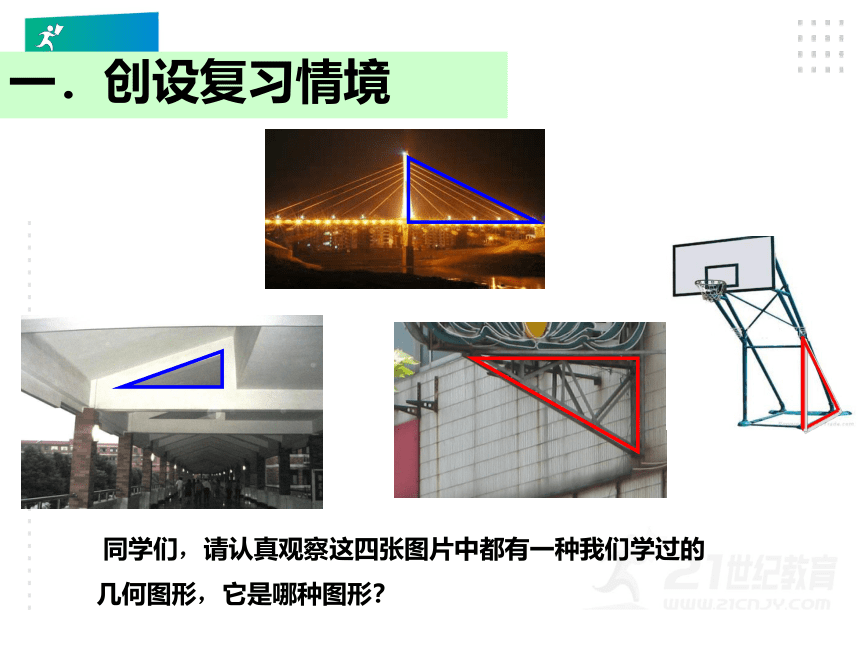
一.创设复习情境
同学们,请认真观察这四张图片中都有一种我们学过的几何图形,它是哪种图形?
1.如图,已知在△ABC
中,∠B
=90°,一直角边为a,斜边为b,则另一直角边c满足c2
=
.
【思考】为什么不是
?
第一组练习:
勾股定理的直接应用
(一)知两边或一边一角型
二.
基础知识运用
答案:因为∠B
所对的边是斜边.
答案:
2.在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4,
则c=
;
(2)如果a=6,c=10,
则b= ;
(3)如果c=13,b=12,则a=
;
(4)已知b=3,∠A=30°,求a,c.
答案:(4)a=
,c=
.
5
8
5
第一组练习:
勾股定理的直接应用
(一)知两边或一边一角型
1.如图,已知在△ABC
中,∠B
=90°,若BC=4
,
AB=x
,AC=8-x,则AB=
,AC=
.
2.在Rt△ABC
中,∠B=90°,b=34,a:c=8:15,则
a=
,
c=
.
3
5
16
30
第一组练习:
勾股定理的直接应用
(二)知一边及另两边关系型
1.
对三角形边的分类.
已知一个直角三角形的两条边长是3
cm和4
cm,求第三条边的长.
注意:这里并没有指明已知的两条边就是直角边,所以4
cm可以是直角边,也可以是斜边,即应分情况讨论.
答案:5
cm或
cm.
第一组练习:
勾股定理的直接应用
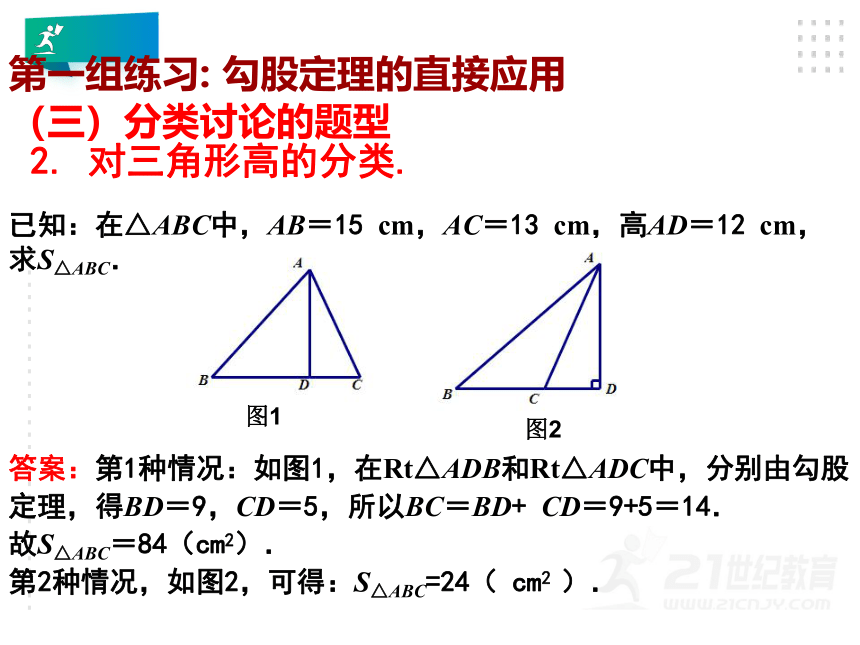
(三)分类讨论的题型
已知:在△ABC中,AB=15
cm,AC=13
cm,高AD=12
cm,求S△ABC.
答案:第1种情况:如图1,在Rt△ADB和Rt△ADC中,分别由勾股定理,得BD=9,CD=5,所以BC=BD+
CD=9+5=14.
故S△ABC=84(cm2).
第2种情况,如图2,可得:S△ABC=24(
cm2
).
2.
对三角形高的分类.
图1
图2
第一组练习:
勾股定理的直接应用
(三)分类讨论的题型
【思考】本组题,利用勾股定理解决了哪些类型题目?注意事项是什么?
利用勾股定理能求三角形的边长和高等线段的长度.注意没有图形的题目,先画图,再考虑是否需分类讨论.
1.
在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?( )
A.一定不会
B.可能会
C.一定会
D.以上答案都不对
A
第二组练习:
用勾股定理解决简单的实际问题
2.
如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑杆顶端A下滑多少米?
A
E
C
B
D
答案:解:设AE的长为x
米,依题意
得CE=AC
-
x
,∵AB=DE=2.5,BC=1.5,
∠C=90°,∴AC=2.∵BD=0.5,∴AC=2.
∴在Rt△ECD中,CE=1.5.
∴2-
x
=1.5,
x
=0.5.
即AE=0.5
.
答:梯子下滑0.5米.
第二组练习:
用勾股定理解决简单的实际问题
答案:是.
证明:在Rt△ACB中,BC=3,AB=5,AC=4.DC=4-1=3.
在Rt△ECD中,DC=3,DE=5,
CE=4.BE=CE-CB=1.
即梯子底端也滑动了1米.
3.(选做题)一架长5米的梯子,斜立在一竖直的墙上,这时梯子底端距墙底3米.
如果梯子的顶端沿墙下滑1米,梯子的底端在水平方向沿一条直线也将滑动1米吗?用所学知识,论证你的结论.
第二组练习:
用勾股定理解决简单的实际问题
思考:利用勾股定理解题决实际问题时,基本步骤是什么?
答案:1.把实际问题转化成数学问题,找出相应的直角三角形.
2.在直角三角形中找出直角边,斜边.
3.根据已知和所求,利用勾股定理解决问题.
1.证明线段相等.
已知:如图,AD是△ABC的高,AB=10,AD=8,BC=12
.
求证:
△ABC是等腰三角形.
?
答案:证明:∵AD是△ABC的高,∴∠ADB=∠ADC=90°.∵在Rt△ADB中,AB=10,AD=8,∴BD=6
.∵BC=12,
∴DC=6.∵在Rt△ADC中,AD=8,∴AC=10,∴AB=AC.即△ABC是等腰三角形.
分析:利用勾股定理求出线段BD的长,也能求出线段AC的长,最后得出AB=AC,即可.
第三组练习:
会用勾股定理解决较综合的问题
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
【思考1】由AB=8,BC=10,你可以知道哪些线段长?请在图中标出来.
答案:AD=10,DC=8
.
第三组练习:
会用勾股定理解决较综合的问题
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考2】
在Rt△DFC中,你可以求出DF的长吗?请在图中标出来.
答案:
DF=6
.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
答案:
AF=4
.
【思考3】
由DF的长,你还可以求出哪条线段长?
请在图中标出来.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考4】
设BE
=
x,你可以用含有x的式子表示出哪些线段长?请在图中标出来.
答案:EF
=
x,AE
=
8-x,CF
=
10
.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考5】
你在哪个直角三角形中,应用勾股定理建立方程?你建立的方程是
.
答案:直角三角形△AEF,
∵∠A=90°,
AE=8-x,
∴
.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考6】
图中共有几个直角三角形?每一个直角三角形的作用是什么?折叠的作用是什么?
答案:
四个,两个用来折叠,将线段和角等量转化,
一个用来知二求一,最后一个建立方程.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考7】
请把你的解答过程写下来.
答案:
设BE=x,折叠,∴△BCE
≌△FCE,
∴BC=FC=10.
令BE=FE=x,长方形ABCD,
∴
AB=DC=8
,AD=BC=10,∠D=90°,
∴DF=6,
AF=4,∠A=90°,
AE=8-x
,
∴
,解得
x
=
5
.∴BE的长为5.
3.做高线,构造直角三角形.
已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=2.求(1)BC
的长;(2)S△ABC?.
分析:由于本题中的△ABC不是直角三角形,所以添加BC边上的高这条辅助线,就可以求得BC及S△ABC?.
第三组练习:
会用勾股定理解决较综合的问题
3.做高线,构造直角三角形.
已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=2.求(1)BC
的长;(2)S△ABC?.
答案:过点A作AD⊥BC于D,∴∠ADB=∠ADC=90°.
在△ABD中,∠ADB=90°,
∠B=45°,AB=2,∴AD=BD=
.∵在△ABD中,∠ADC=90°,∠C=60°,AD=
,
∴CD=
,∴BC=
,S△ABC?=
第三组练习:
会用勾股定理解决较综合的问题
思考
:在不是直角三角形中如何求线段长和面积?
解一般三角形的问题常常通过作高转化成直角三角形,利用勾股定理解决问题.
思考:利用勾股定理解决综合题的基本步骤是什么?
1.画图与标图,根据题目要求添加辅助线,
构造直角三角形.
2.将已知量与未知量集中到同一个直角三角
形中.
3
.利用勾股定理列出方程.
4.解方程,求线段长,最后完成解题.
1.下列线段不能组成直角三角形的是(
)
A.a=8,b=15,c=17
B.a=9,b=12,c=15
C.a=
,b=
,c=
D.a:b:c=2:3:4
2.如图,在由单位正方形组成的网格图中标有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的是( )
A.CD,EF,GH
B.AB,EF,GH
C.AB,CD,GH
D.AB,CD,EF
C
E
B
H
D
F
A
G
D
B
第四组练习:
勾股定理的逆定理的应用
已知:如图,四边形ABCD,AB=1,BC=2,CD=2,AD=3,
且AB⊥BC.求四边形
ABCD的面积.
分析:本题解题的关键是恰当的添加辅助线,利用勾股定理的逆定理判定△ADC的形状为直角三角形,再利用勾股定理解题.
答案:连接AC,∵AB⊥BC,∴∠ABC=90°.
∵在△ABC中,∠ABC=90°,AB=1,BC=2,
∴AC=
.∵CD=2,AD=3,
∴△ACD是直角三角形;∴四边形的面积为1+
.
第五组练习:
勾股定理及其逆定理的综合应用
你在本节课的收获是什么?
还有什么困惑?
三.
课堂小结
1.一个直角三角形的两边长分别为4、5,那么第三条边长为______.
2.已知:如图,等边△ABC的边长是6
cm.
求⑴等边△ABC的高;
⑵S△ABC.
3.(选做题)如图,AB=AC=20,BC=32,
∠DAC=90°,求BD的长.
四.
布置作业
1.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处.已知BC=12,∠B=30°,
则DE的长是(
).
A.6
B.4
C.3
D.2
2.一个直角三角形的两条边长分别是6
cm和8
cm,那么这个三角形的周长和面积分别是多少?
3.如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便估算产量.小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°.
答案:2.(1)周长是24
cm,面积是24
cm2;
(2)周长是
cm
,面积是
cm2.
B
答案:
3.36平方米.
五.
课堂反馈
https://www.21cnjy.com/help/help_extract.php
第十七章
勾股定理
章末小结
人教版
八年级下册
一.创设复习情境
同学们,请认真观察这四张图片中都有一种我们学过的几何图形,它是哪种图形?
1.如图,已知在△ABC
中,∠B
=90°,一直角边为a,斜边为b,则另一直角边c满足c2
=
.
【思考】为什么不是
?
第一组练习:
勾股定理的直接应用
(一)知两边或一边一角型
二.
基础知识运用
答案:因为∠B
所对的边是斜边.
答案:
2.在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4,
则c=
;
(2)如果a=6,c=10,
则b= ;
(3)如果c=13,b=12,则a=
;
(4)已知b=3,∠A=30°,求a,c.
答案:(4)a=
,c=
.
5
8
5
第一组练习:
勾股定理的直接应用
(一)知两边或一边一角型
1.如图,已知在△ABC
中,∠B
=90°,若BC=4
,
AB=x
,AC=8-x,则AB=
,AC=
.
2.在Rt△ABC
中,∠B=90°,b=34,a:c=8:15,则
a=
,
c=
.
3
5
16
30
第一组练习:
勾股定理的直接应用
(二)知一边及另两边关系型
1.
对三角形边的分类.
已知一个直角三角形的两条边长是3
cm和4
cm,求第三条边的长.
注意:这里并没有指明已知的两条边就是直角边,所以4
cm可以是直角边,也可以是斜边,即应分情况讨论.
答案:5
cm或
cm.
第一组练习:
勾股定理的直接应用
(三)分类讨论的题型
已知:在△ABC中,AB=15
cm,AC=13
cm,高AD=12
cm,求S△ABC.
答案:第1种情况:如图1,在Rt△ADB和Rt△ADC中,分别由勾股定理,得BD=9,CD=5,所以BC=BD+
CD=9+5=14.
故S△ABC=84(cm2).
第2种情况,如图2,可得:S△ABC=24(
cm2
).
2.
对三角形高的分类.
图1
图2
第一组练习:
勾股定理的直接应用
(三)分类讨论的题型
【思考】本组题,利用勾股定理解决了哪些类型题目?注意事项是什么?
利用勾股定理能求三角形的边长和高等线段的长度.注意没有图形的题目,先画图,再考虑是否需分类讨论.
1.
在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?( )
A.一定不会
B.可能会
C.一定会
D.以上答案都不对
A
第二组练习:
用勾股定理解决简单的实际问题
2.
如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑杆顶端A下滑多少米?
A
E
C
B
D
答案:解:设AE的长为x
米,依题意
得CE=AC
-
x
,∵AB=DE=2.5,BC=1.5,
∠C=90°,∴AC=2.∵BD=0.5,∴AC=2.
∴在Rt△ECD中,CE=1.5.
∴2-
x
=1.5,
x
=0.5.
即AE=0.5
.
答:梯子下滑0.5米.
第二组练习:
用勾股定理解决简单的实际问题
答案:是.
证明:在Rt△ACB中,BC=3,AB=5,AC=4.DC=4-1=3.
在Rt△ECD中,DC=3,DE=5,
CE=4.BE=CE-CB=1.
即梯子底端也滑动了1米.
3.(选做题)一架长5米的梯子,斜立在一竖直的墙上,这时梯子底端距墙底3米.
如果梯子的顶端沿墙下滑1米,梯子的底端在水平方向沿一条直线也将滑动1米吗?用所学知识,论证你的结论.
第二组练习:
用勾股定理解决简单的实际问题
思考:利用勾股定理解题决实际问题时,基本步骤是什么?
答案:1.把实际问题转化成数学问题,找出相应的直角三角形.
2.在直角三角形中找出直角边,斜边.
3.根据已知和所求,利用勾股定理解决问题.
1.证明线段相等.
已知:如图,AD是△ABC的高,AB=10,AD=8,BC=12
.
求证:
△ABC是等腰三角形.
?
答案:证明:∵AD是△ABC的高,∴∠ADB=∠ADC=90°.∵在Rt△ADB中,AB=10,AD=8,∴BD=6
.∵BC=12,
∴DC=6.∵在Rt△ADC中,AD=8,∴AC=10,∴AB=AC.即△ABC是等腰三角形.
分析:利用勾股定理求出线段BD的长,也能求出线段AC的长,最后得出AB=AC,即可.
第三组练习:
会用勾股定理解决较综合的问题
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
【思考1】由AB=8,BC=10,你可以知道哪些线段长?请在图中标出来.
答案:AD=10,DC=8
.
第三组练习:
会用勾股定理解决较综合的问题
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考2】
在Rt△DFC中,你可以求出DF的长吗?请在图中标出来.
答案:
DF=6
.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
答案:
AF=4
.
【思考3】
由DF的长,你还可以求出哪条线段长?
请在图中标出来.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考4】
设BE
=
x,你可以用含有x的式子表示出哪些线段长?请在图中标出来.
答案:EF
=
x,AE
=
8-x,CF
=
10
.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考5】
你在哪个直角三角形中,应用勾股定理建立方程?你建立的方程是
.
答案:直角三角形△AEF,
∵∠A=90°,
AE=8-x,
∴
.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考6】
图中共有几个直角三角形?每一个直角三角形的作用是什么?折叠的作用是什么?
答案:
四个,两个用来折叠,将线段和角等量转化,
一个用来知二求一,最后一个建立方程.
2.解决折叠的问题.
已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10,
求BE的长.
第三组练习:
会用勾股定理解决较综合的问题
【思考7】
请把你的解答过程写下来.
答案:
设BE=x,折叠,∴△BCE
≌△FCE,
∴BC=FC=10.
令BE=FE=x,长方形ABCD,
∴
AB=DC=8
,AD=BC=10,∠D=90°,
∴DF=6,
AF=4,∠A=90°,
AE=8-x
,
∴
,解得
x
=
5
.∴BE的长为5.
3.做高线,构造直角三角形.
已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=2.求(1)BC
的长;(2)S△ABC?.
分析:由于本题中的△ABC不是直角三角形,所以添加BC边上的高这条辅助线,就可以求得BC及S△ABC?.
第三组练习:
会用勾股定理解决较综合的问题
3.做高线,构造直角三角形.
已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=2.求(1)BC
的长;(2)S△ABC?.
答案:过点A作AD⊥BC于D,∴∠ADB=∠ADC=90°.
在△ABD中,∠ADB=90°,
∠B=45°,AB=2,∴AD=BD=
.∵在△ABD中,∠ADC=90°,∠C=60°,AD=
,
∴CD=
,∴BC=
,S△ABC?=
第三组练习:
会用勾股定理解决较综合的问题
思考
:在不是直角三角形中如何求线段长和面积?
解一般三角形的问题常常通过作高转化成直角三角形,利用勾股定理解决问题.
思考:利用勾股定理解决综合题的基本步骤是什么?
1.画图与标图,根据题目要求添加辅助线,
构造直角三角形.
2.将已知量与未知量集中到同一个直角三角
形中.
3
.利用勾股定理列出方程.
4.解方程,求线段长,最后完成解题.
1.下列线段不能组成直角三角形的是(
)
A.a=8,b=15,c=17
B.a=9,b=12,c=15
C.a=
,b=
,c=
D.a:b:c=2:3:4
2.如图,在由单位正方形组成的网格图中标有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的是( )
A.CD,EF,GH
B.AB,EF,GH
C.AB,CD,GH
D.AB,CD,EF
C
E
B
H
D
F
A
G
D
B
第四组练习:
勾股定理的逆定理的应用
已知:如图,四边形ABCD,AB=1,BC=2,CD=2,AD=3,
且AB⊥BC.求四边形
ABCD的面积.
分析:本题解题的关键是恰当的添加辅助线,利用勾股定理的逆定理判定△ADC的形状为直角三角形,再利用勾股定理解题.
答案:连接AC,∵AB⊥BC,∴∠ABC=90°.
∵在△ABC中,∠ABC=90°,AB=1,BC=2,
∴AC=
.∵CD=2,AD=3,
∴△ACD是直角三角形;∴四边形的面积为1+
.
第五组练习:
勾股定理及其逆定理的综合应用
你在本节课的收获是什么?
还有什么困惑?
三.
课堂小结
1.一个直角三角形的两边长分别为4、5,那么第三条边长为______.
2.已知:如图,等边△ABC的边长是6
cm.
求⑴等边△ABC的高;
⑵S△ABC.
3.(选做题)如图,AB=AC=20,BC=32,
∠DAC=90°,求BD的长.
四.
布置作业
1.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处.已知BC=12,∠B=30°,
则DE的长是(
).
A.6
B.4
C.3
D.2
2.一个直角三角形的两条边长分别是6
cm和8
cm,那么这个三角形的周长和面积分别是多少?
3.如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便估算产量.小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°.
答案:2.(1)周长是24
cm,面积是24
cm2;
(2)周长是
cm
,面积是
cm2.
B
答案:
3.36平方米.
五.
课堂反馈
https://www.21cnjy.com/help/help_extract.php
