第四讲 估算(考点讲解)（含答案）

中小学教育资源及组卷应用平台
第四讲
估算
【学习目标】
会估算一个无理数的大致范围，比较两个无理数的大小
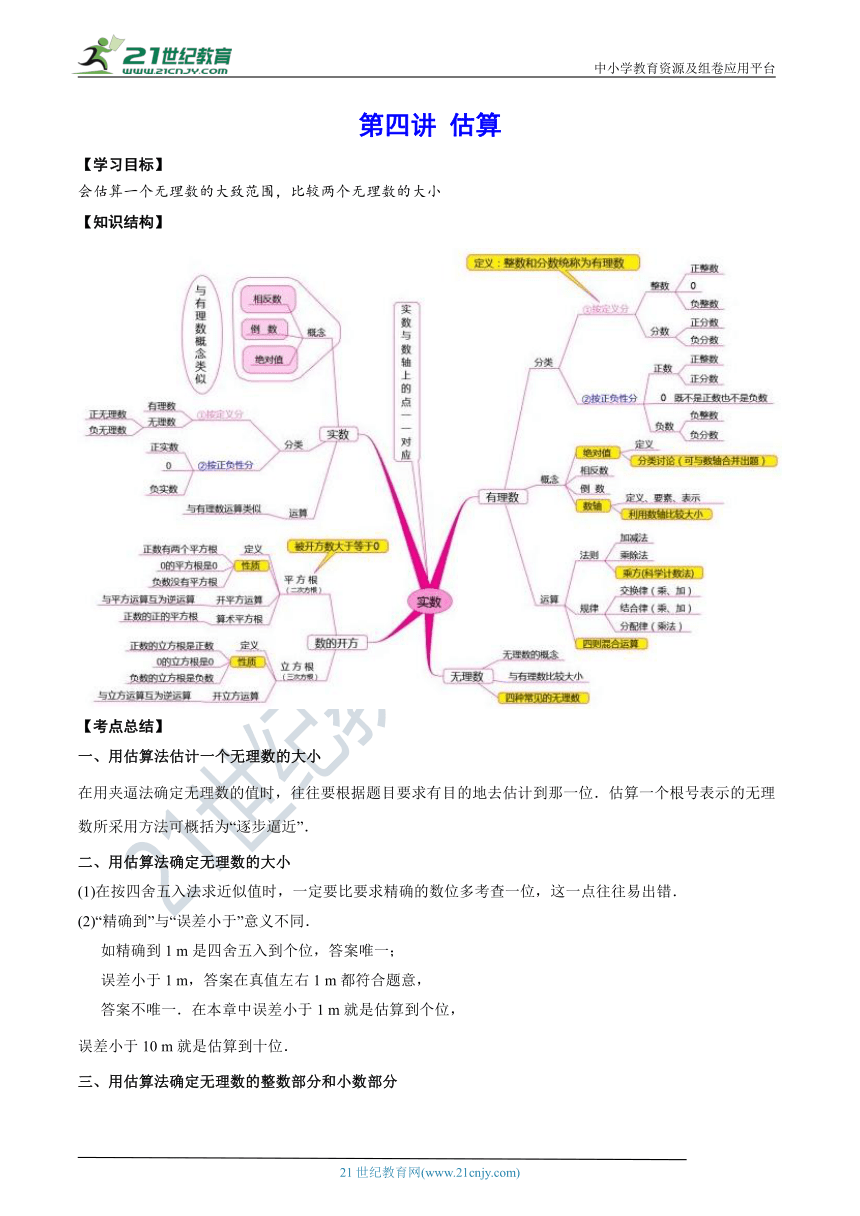
【知识结构】
(?http:?/??/?www.21cnjy.com?/??)
【考点总结】
一、用估算法估计一个无理数的大小
在用夹逼法确定无理数的值时，往往要根据题目要求有目的地去估计到那一位．估算一个根号表示的无理数所采用方法可概括为“逐步逼近”．21世纪教育网版权所有
二、用估算法确定无理数的大小
(1)在按四舍五入法求近似值时，一定要比要求精确的数位多考查一位，这一点往往易出错．
(2)“精确到”与“误差小于”意义不同．
如精确到1
m是四舍五入到个位，答案唯一；
误差小于1
m，答案在真值左右1
m都符合题意，
答案不唯一．在本章中误差小于1
m就是估算到个位，
误差小于10
m就是估算到十位．
三、用估算法确定无理数的整数部分和小数部分
关键要先估算整数部分，只要整数部分估算出来了，小数部分随之就写出来了．一个无理数减去它的整数部分，剩下的就是它的小数部分．21教育网
四、比较两个无理数的大小
两个有理数的大小比较方法较多，
1、
比如将它们化为小数再比较，先对无理数求近似值，然后比较．当然，
2、
还有许多特殊的方法，比如平方法、作差法、估算法等．
合理的选用特殊方法比较数的大小，会让运算变得简单．
用估算法比较含根号的数的大小，一般可采取下列方法：
(1)先估算含根号的数的近似值，再和另一个数进行比较；
(2)当符号相同时，把不含根号的数平方，和含根号的数的被开方数比较．
本方法的实质是比较被开方数，被开方数越大，其算术平方根越大；
(3)若同分母或同分子的，可比较它们分子或分母的大小．
五、估算的实际应用
在生产生活中，我们经常遇到求距离、高度、长度、深度等一些线段长度的问题，在很多情况下得到的是无理数，根据实际需要，一般情况下只需取无理数的近似值就可以了．要求无理数的近似值，首先需要用估算的方法确定无理数的大致范围，估算无理数经常用到“夹逼法”，即利用乘方与开方互为逆运算来确定无理数的近似值．
21·cn·jy·com
【例题讲解】
【类型】一、估计取值范围
例1．（1）1．估计的值应在（
）
A．4和5之间
B．3和4之间
C．2和3之间
D．1和2之间
【答案】B
【详解】
解：∵，，
∴，
∴，
∴，
故选B．
（2）如图，长方形的长为3，宽为2，对角线为，且，则下列各数中与点表示的数最接近的是（
）21cnjy.com
(?http:?/??/?www.21cnjy.com?/??)
A．-3.5
B．-3.6
C．-3.7
D．-3.8
【答案】B
【详解】
解：∵长方形的长为3，宽为2，
∴，
∴A所表示的数为，
∵，，
∴介于-3.6和-3.7之间，
∵，
∴比较接近-3.6，
故选：B．
例2．我们知道面积为8的正方形的边长为
(?http:?/??/?www.21cnjy.com?/??)
（1）在方格图中画出面积为8的正方形．
（2）若的整数部分为a，小数部分为b，请你求的相反数
【答案】（1）见解析；（2）
【详解】
解：（1）如图所示：
(?http:?/??/?www.21cnjy.com?/??)
（2）∵，
∴，
∴，
∴，
∴a=3，b==，
∴==，
∴的相反数是．
【类型】二、无理数整数部分的估算与计算
例3．已知的平方根是的立方根是是的整数部分，求的算术平方根．
【答案】
【详解】
解：根据题意，可得2a?1＝9，
a＋3b?1＝-8；
解得：a＝5，b＝-4；
又∵6＜＜7，
可得c＝6；
∴a＋2b＋c＝3；
∴a＋2b＋c的算术平方根为．
例4．5a﹣4的立方根是﹣4，25的平方根是5与b+15，c是的整数部分．
（1）求a、b、c的值；
（2）求b+c﹣2a的算术平方根．
【答案】（1）a=﹣12，b=﹣20，c=3；（2）
【详解】
解：（1）∵5a﹣4的立方根是﹣4，25的平方根是5与b+15，
∴5a﹣4=（﹣4）3，b+15=﹣5，
解得：a=﹣12，b=﹣20，
∵3＜＜4，
∴的整数部分是3，
∴c=3；
（2）当a=﹣12，b=﹣20，c=3时，
b+c﹣2a=﹣20+3﹣2×（﹣12）=7，
∴b+c﹣2a的算术平方根为．
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)