2020-2021学年河北省唐山市丰南区九年级(上)月考数学试卷(12月份)(word解析版)
文档属性
| 名称 | 2020-2021学年河北省唐山市丰南区九年级(上)月考数学试卷(12月份)(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 00:00:00 | ||
图片预览


文档简介
2020-2021学年河北省唐山市丰南区九年级(上)月考数学试卷(12月份)
一、选择题(每题3分,共39分)
1.(3分)小华在解方程时,得,则他漏掉的一个根是
A.
B.
C.
D.
2.(3分)从下列四张卡片中任取一张,卡片上的图形是中心对称图形的概率为
A.0
B.
C.
D.
3.(3分)如图,是的直径,是的弦,若,则的大小为
A.
B.
C.
D.
4.(3分)给出下列函数,其中随的增大而减小的函数是
①;②;③;④.
A.①③④
B.②③④
C.②④
D.②③
5.(3分)如图,四边形是的内接四边形,的半径为6,,则劣弧的长为
A.
B.
C.
D.
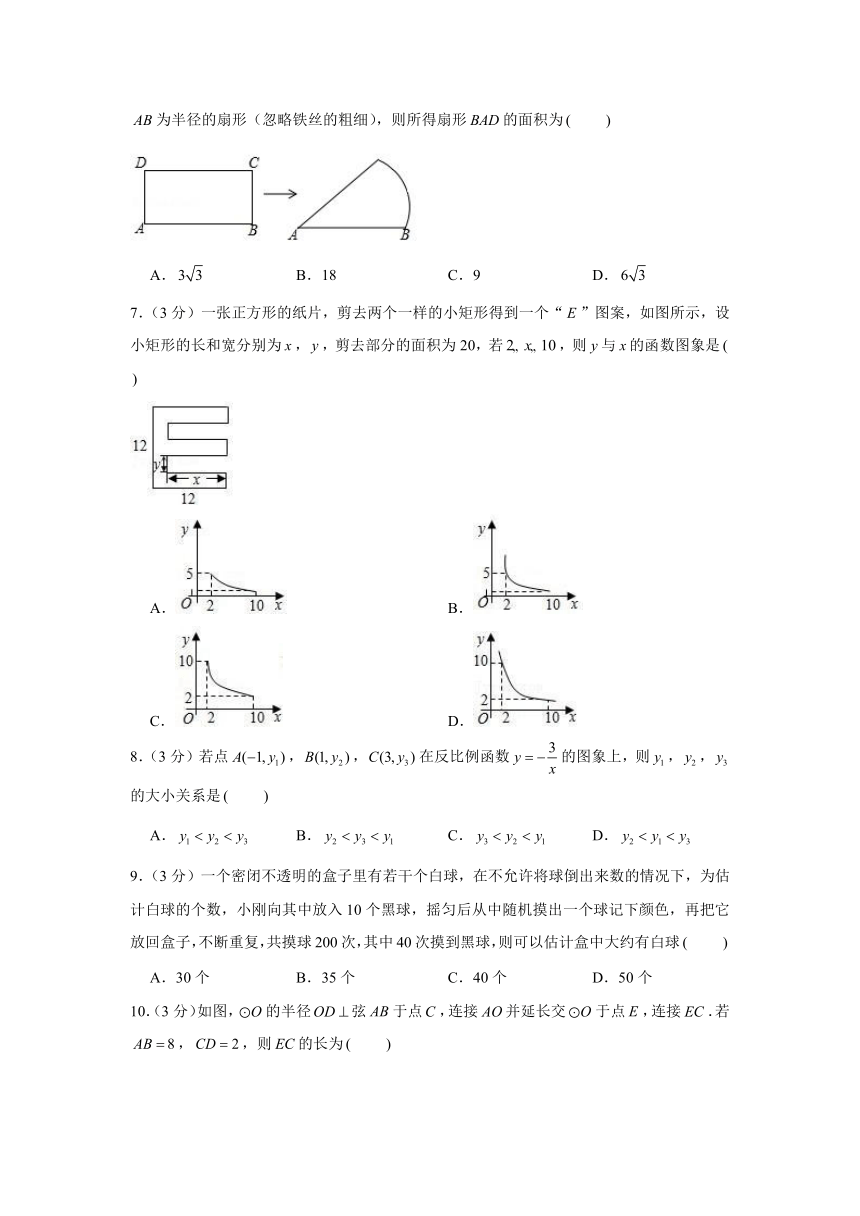
6.(3分)如图,某数学兴趣小组将长为6,宽为3的矩形铁丝框变形为以为圆心,为半径的扇形(忽略铁丝的粗细),则所得扇形的面积为
A.
B.18
C.9
D.
7.(3分)一张正方形的纸片,剪去两个一样的小矩形得到一个“”图案,如图所示,设小矩形的长和宽分别为,,剪去部分的面积为20,若,则与的函数图象是
A.
B.
C.
D.
8.(3分)若点,,在反比例函数的图象上,则,,的大小关系是
A.
B.
C.
D.
9.(3分)一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球的个数,小刚向其中放入10个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子,不断重复,共摸球200次,其中40次摸到黑球,则可以估计盒中大约有白球
A.30个
B.35个
C.40个
D.50个
10.(3分)如图,的半径弦于点,连接并延长交于点,连接.若,,则的长为
A.
B.
C.
D.8
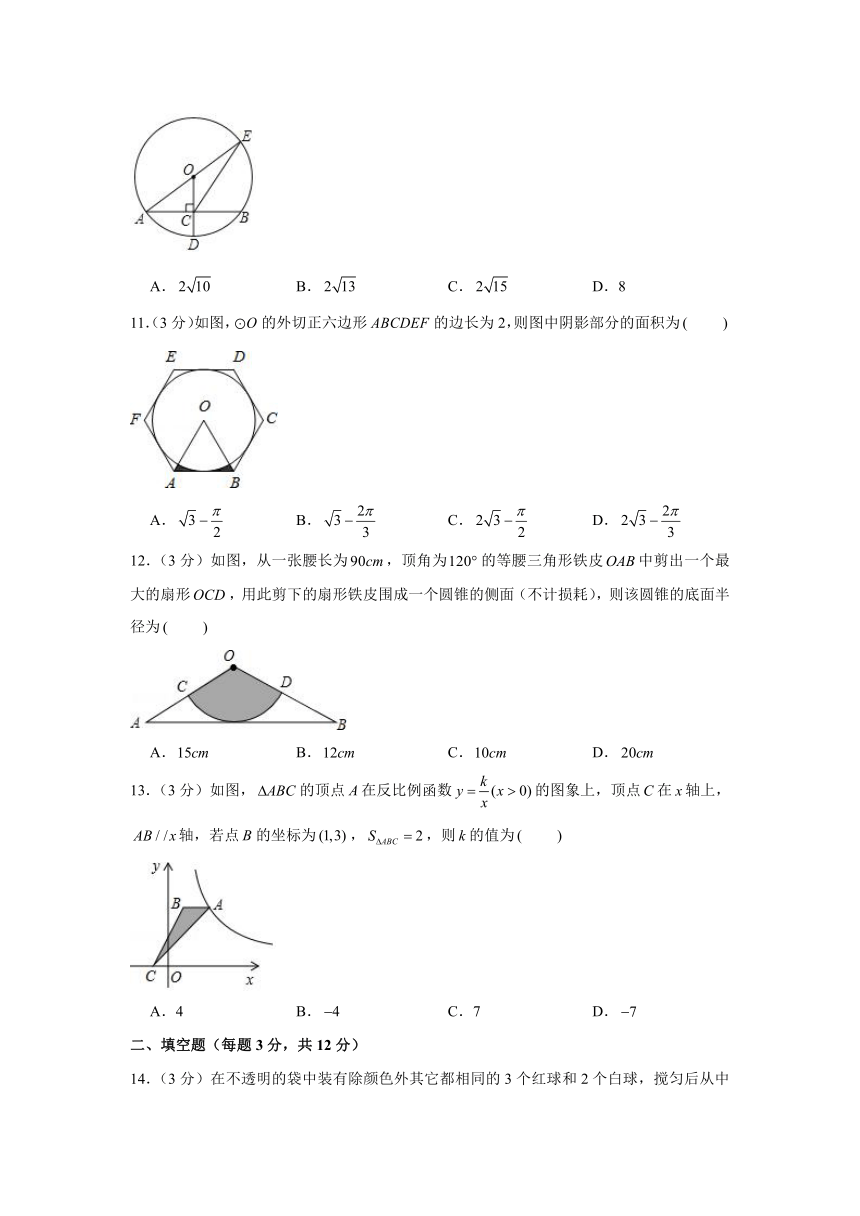
11.(3分)如图,的外切正六边形的边长为2,则图中阴影部分的面积为
A.
B.
C.
D.
12.(3分)如图,从一张腰长为,顶角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为
A.
B.
C.
D.
13.(3分)如图,的顶点在反比例函数的图象上,顶点在轴上,轴,若点的坐标为,,则的值为
A.4
B.
C.7
D.
二、填空题(每题3分,共12分)
14.(3分)在不透明的袋中装有除颜色外其它都相同的3个红球和2个白球,搅匀后从中随机摸出2个球,则摸出的两个球恰好一红一白的概率是 .
15.(3分)如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,以为边在第一象限作正方形,点恰好在双曲线上,则值为 .
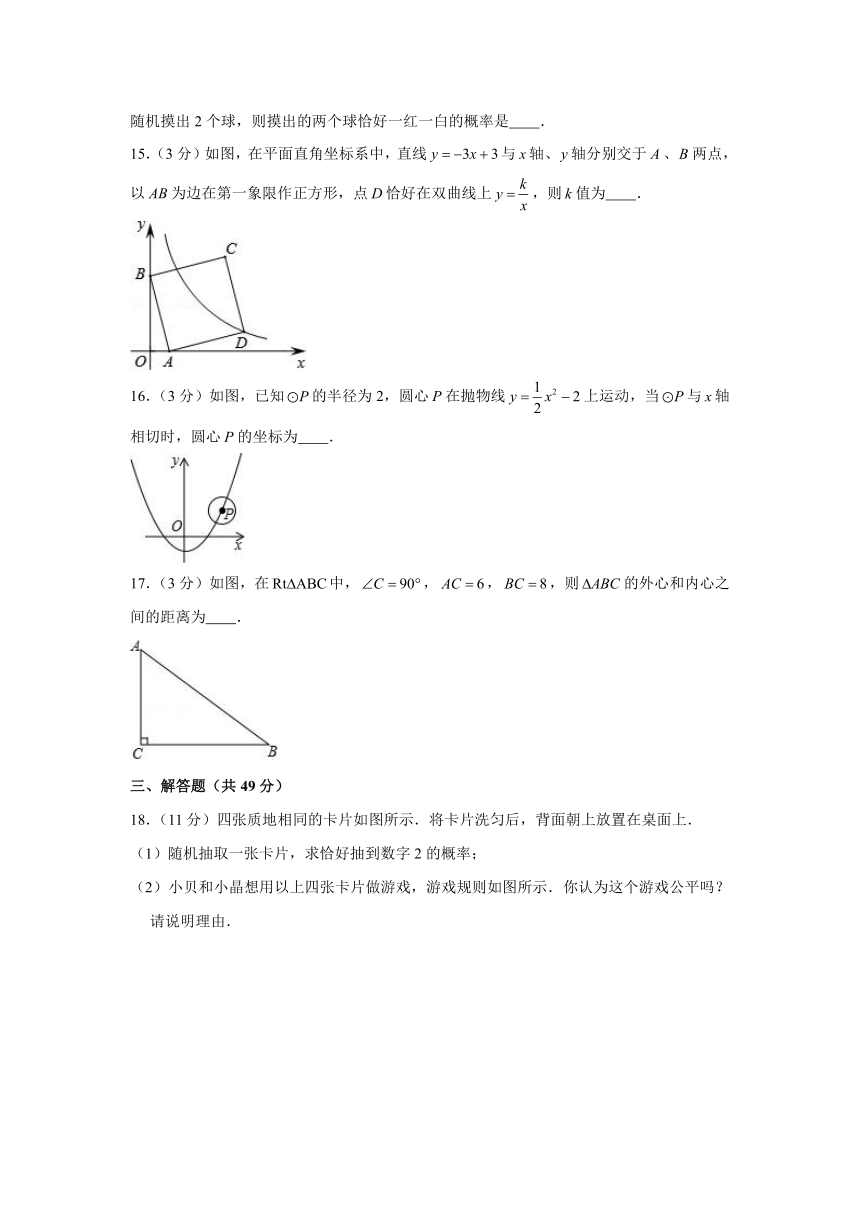
16.(3分)如图,已知的半径为2,圆心在抛物线上运动,当与轴相切时,圆心的坐标为 .
17.(3分)如图,在中,,,,则的外心和内心之间的距离为 .
三、解答题(共49分)
18.(11分)四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
(1)随机抽取一张卡片,求恰好抽到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则如图所示.你认为这个游戏公平吗?请说明理由.
19.(12分)在平面直角坐标系中,直线与双曲线相交于点.
(1)求反比例函数的表达式;
(2)画出双曲线的示意图;
(3)若另一个交点的坐标为,则 ;当时,的取值范围为
;
(4)观察反比例函数的图象,当时,自变量的取值范围是
.
20.(12分)如图,已知在中,,,延长到,使,以为圆心,长为半径作交延长线于点,连接.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积.
21.(14分)如图,已知在平面直角坐标系中,矩形的边轴,轴,点的坐标位,,.
(1)求直线的解析式;
(2)已知双曲线与折线的交点为,与折线的交点为.
①连接,当时,求该双曲线的解析式,并求出此时点的坐标;
②若双曲线与矩形各边和对角线的交点个数为3,请直接写出的取值范围.
参考答案与试题解析
一、选择题(每题3分,共39分)
1.(3分)小华在解方程时,得,则他漏掉的一个根是
A.
B.
C.
D.
【解答】解:方程移项得:,
分解因式得:,
解得:,,
则他漏掉的一个根式,
故选:.
2.(3分)从下列四张卡片中任取一张,卡片上的图形是中心对称图形的概率为
A.0
B.
C.
D.
【解答】解:在这一组图形中,中心对称图形只有最后一个,
卡片上的图形是中心对称图形的概率是.
故选:.
3.(3分)如图,是的直径,是的弦,若,则的大小为
A.
B.
C.
D.
【解答】解:连接,
是的直径,
,
,
.
故选:.
4.(3分)给出下列函数,其中随的增大而减小的函数是
①;②;③;④.
A.①③④
B.②③④
C.②④
D.②③
【解答】解:①中,随的增大而增大,故本小题不合题意;
②中,随的增大而减小,故本小题符合题意;
③中,时,随的增大而减小,故本小题符合题意;
④中,当时,随的增大而增大,故本小题不合题意.
故选:.
5.(3分)如图,四边形是的内接四边形,的半径为6,,则劣弧的长为
A.
B.
C.
D.
【解答】解:如图,连接,.
,,
,
,
的长,
故选:.
6.(3分)如图,某数学兴趣小组将长为6,宽为3的矩形铁丝框变形为以为圆心,为半径的扇形(忽略铁丝的粗细),则所得扇形的面积为
A.
B.18
C.9
D.
【解答】解:矩形的长为6,宽为3,
,,
弧的弧长,
.
故选:.
7.(3分)一张正方形的纸片,剪去两个一样的小矩形得到一个“”图案,如图所示,设小矩形的长和宽分别为,,剪去部分的面积为20,若,则与的函数图象是
A.
B.
C.
D.
【解答】解:是剪去的两个矩形,两个矩形的面积和为20,
,
是的反比例函数,
,
答案为.
故选:.
8.(3分)若点,,在反比例函数的图象上,则,,的大小关系是
A.
B.
C.
D.
【解答】解:,
在第四象限,随的增大而增大,
,
,
,
故选:.
9.(3分)一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球的个数,小刚向其中放入10个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子,不断重复,共摸球200次,其中40次摸到黑球,则可以估计盒中大约有白球
A.30个
B.35个
C.40个
D.50个
【解答】解:设盒子里有白球个,
根据得:
解得:.
故选:.
10.(3分)如图,的半径弦于点,连接并延长交于点,连接.若,,则的长为
A.
B.
C.
D.8
【解答】解:连接,
设半径为,则,,
,
,
,
在中,由勾股定理得:,
,
,
为的直径,
,
由勾股定理得:,
在中,.
故选:.
11.(3分)如图,的外切正六边形的边长为2,则图中阴影部分的面积为
A.
B.
C.
D.
【解答】解:六边形是正六边形,
,
是等边三角形,,
设点为与的切点,连接,则,
,
.
故选:.
12.(3分)如图,从一张腰长为,顶角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为
A.
B.
C.
D.
【解答】解:过作于,,,
,
,
弧的长,
设圆锥的底面圆的半径为,则,解得.
故选:.
13.(3分)如图,的顶点在反比例函数的图象上,顶点在轴上,轴,若点的坐标为,,则的值为
A.4
B.
C.7
D.
【解答】解:轴,若点的坐标为,
设点
点,
点在反比例函数的图象上,
故选:.
二、填空题(每题3分,共12分)
14.(3分)在不透明的袋中装有除颜色外其它都相同的3个红球和2个白球,搅匀后从中随机摸出2个球,则摸出的两个球恰好一红一白的概率是 .
【解答】解:列表如下:
红
红
红
白
白
红
(红,红)
(红,红)
(红,白)
(红,白)
红
(红,红)
(红,红)
(红,白)
(红,白)
红
(红,红)
(红,红)
(红,白)
(红,白)
白
(白,红)
(白,红)
(白,红)
(白,白)
白
(白,红)
(白,红)
(白,红)
(白,白)
由树状图知,共有20种等可能结果,其中摸出的两个球恰好一红一白的有12种结果,
摸出的两个球恰好一红一白的概率为,
故答案为:.
15.(3分)如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,以为边在第一象限作正方形,点恰好在双曲线上,则值为 4 .
【解答】解:作轴于点.
在中,令,解得:,即的坐标是.
令,解得:,即的坐标是.
则,.
,
,
又中,,
,
在和中,
,
,
,,
故的坐标是,
代入得:,
故答案为:4.
16.(3分)如图,已知的半径为2,圆心在抛物线上运动,当与轴相切时,圆心的坐标为 ,或,或 .
【解答】解:与轴相切,点到轴的距离为2,即,
当时,,
解得:;
当时,,
解得:;
故圆心的坐标为:,或,或.
故答案为:,或,或.
17.(3分)如图,在中,,,,则的外心和内心之间的距离为 .
【解答】解:设的内切圆,为的外接圆的圆心,过点作于,于,于,
在中,,,,
,
点为的外心,
为外接圆半径,,
设的半径为,则,
又,
四边形是正方形,
,,,
,
解得:,
,,
在中,,,
,
故答案为:.
三、解答题(共49分)
18.(11分)四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
(1)随机抽取一张卡片,求恰好抽到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则如图所示.你认为这个游戏公平吗?请说明理由.
【解答】解:(1)(抽到数字.(2分)
(2)公平.
列表:
2
2
3
6
2
2
3
6
由上表可以看出,可能出现的结果共有16种,它们出现的可能性相同,所有的结果中,满足两位数不超过30的结果有8种.(5分)
所以(小贝胜),(小晶胜).所以游戏公平.(7分)
19.(12分)在平面直角坐标系中,直线与双曲线相交于点.
(1)求反比例函数的表达式;
(2)画出双曲线的示意图;
(3)若另一个交点的坐标为,则 ;当时,的取值范围为
;
(4)观察反比例函数的图象,当时,自变量的取值范围是
.
【解答】解:(1)直线与双曲线相交于点,
,
.
,
把代入,
,
反比例函数的表达式为;
(2)双曲线的示意图如图所示:
(3)直线与双曲线相交于另一个交点的坐标为,
,
,
,
由图象可知:当时,的取值范围或,
故答案为,或.
(4)观察图象,当时,自变量的取值范围是或,
故答案为或.
20.(12分)如图,已知在中,,,延长到,使,以为圆心,长为半径作交延长线于点,连接.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积.
【解答】(1)证明:连接,
,,
,
,
是等边三角形,
,,
,
,
即,
为半径,
是的切线;
(2)解:,,,
,
由勾股定理得:,
.
21.(14分)如图,已知在平面直角坐标系中,矩形的边轴,轴,点的坐标位,,.
(1)求直线的解析式;
(2)已知双曲线与折线的交点为,与折线的交点为.
①连接,当时,求该双曲线的解析式,并求出此时点的坐标;
②若双曲线与矩形各边和对角线的交点个数为3,请直接写出的取值范围.
【解答】解:(1),,,
,.
设直线的解析式为,
将,分别代人,
得,解得,
故直线的解析式为;
(2)①当时,,
,
,
又,
.
将点代人,
,
故该双曲线的解析式为,
将代人,得,
;
②或,
当双曲线经过点,即时,有2个交点;
当线经过点,即时,有3个交点,
故当时,有3个交点,
当双曲线与直线相切时,有3个交点,令,整理得,
当△时,双曲线与直线相切,此时,
或.
一、选择题(每题3分,共39分)
1.(3分)小华在解方程时,得,则他漏掉的一个根是
A.
B.
C.
D.
2.(3分)从下列四张卡片中任取一张,卡片上的图形是中心对称图形的概率为
A.0
B.
C.
D.
3.(3分)如图,是的直径,是的弦,若,则的大小为
A.
B.
C.
D.
4.(3分)给出下列函数,其中随的增大而减小的函数是
①;②;③;④.
A.①③④
B.②③④
C.②④
D.②③
5.(3分)如图,四边形是的内接四边形,的半径为6,,则劣弧的长为
A.
B.
C.
D.
6.(3分)如图,某数学兴趣小组将长为6,宽为3的矩形铁丝框变形为以为圆心,为半径的扇形(忽略铁丝的粗细),则所得扇形的面积为
A.
B.18
C.9
D.
7.(3分)一张正方形的纸片,剪去两个一样的小矩形得到一个“”图案,如图所示,设小矩形的长和宽分别为,,剪去部分的面积为20,若,则与的函数图象是
A.
B.
C.
D.
8.(3分)若点,,在反比例函数的图象上,则,,的大小关系是
A.
B.
C.
D.
9.(3分)一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球的个数,小刚向其中放入10个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子,不断重复,共摸球200次,其中40次摸到黑球,则可以估计盒中大约有白球
A.30个
B.35个
C.40个
D.50个
10.(3分)如图,的半径弦于点,连接并延长交于点,连接.若,,则的长为
A.
B.
C.
D.8
11.(3分)如图,的外切正六边形的边长为2,则图中阴影部分的面积为
A.
B.
C.
D.
12.(3分)如图,从一张腰长为,顶角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为
A.
B.
C.
D.
13.(3分)如图,的顶点在反比例函数的图象上,顶点在轴上,轴,若点的坐标为,,则的值为
A.4
B.
C.7
D.
二、填空题(每题3分,共12分)
14.(3分)在不透明的袋中装有除颜色外其它都相同的3个红球和2个白球,搅匀后从中随机摸出2个球,则摸出的两个球恰好一红一白的概率是 .
15.(3分)如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,以为边在第一象限作正方形,点恰好在双曲线上,则值为 .
16.(3分)如图,已知的半径为2,圆心在抛物线上运动,当与轴相切时,圆心的坐标为 .
17.(3分)如图,在中,,,,则的外心和内心之间的距离为 .
三、解答题(共49分)
18.(11分)四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
(1)随机抽取一张卡片,求恰好抽到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则如图所示.你认为这个游戏公平吗?请说明理由.
19.(12分)在平面直角坐标系中,直线与双曲线相交于点.
(1)求反比例函数的表达式;
(2)画出双曲线的示意图;
(3)若另一个交点的坐标为,则 ;当时,的取值范围为
;
(4)观察反比例函数的图象,当时,自变量的取值范围是
.
20.(12分)如图,已知在中,,,延长到,使,以为圆心,长为半径作交延长线于点,连接.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积.
21.(14分)如图,已知在平面直角坐标系中,矩形的边轴,轴,点的坐标位,,.
(1)求直线的解析式;
(2)已知双曲线与折线的交点为,与折线的交点为.
①连接,当时,求该双曲线的解析式,并求出此时点的坐标;
②若双曲线与矩形各边和对角线的交点个数为3,请直接写出的取值范围.
参考答案与试题解析
一、选择题(每题3分,共39分)
1.(3分)小华在解方程时,得,则他漏掉的一个根是
A.
B.
C.
D.
【解答】解:方程移项得:,
分解因式得:,
解得:,,
则他漏掉的一个根式,
故选:.
2.(3分)从下列四张卡片中任取一张,卡片上的图形是中心对称图形的概率为
A.0
B.
C.
D.
【解答】解:在这一组图形中,中心对称图形只有最后一个,
卡片上的图形是中心对称图形的概率是.
故选:.
3.(3分)如图,是的直径,是的弦,若,则的大小为
A.
B.
C.
D.
【解答】解:连接,
是的直径,
,
,
.
故选:.
4.(3分)给出下列函数,其中随的增大而减小的函数是
①;②;③;④.
A.①③④
B.②③④
C.②④
D.②③
【解答】解:①中,随的增大而增大,故本小题不合题意;
②中,随的增大而减小,故本小题符合题意;
③中,时,随的增大而减小,故本小题符合题意;
④中,当时,随的增大而增大,故本小题不合题意.
故选:.
5.(3分)如图,四边形是的内接四边形,的半径为6,,则劣弧的长为
A.
B.
C.
D.
【解答】解:如图,连接,.
,,
,
,
的长,
故选:.
6.(3分)如图,某数学兴趣小组将长为6,宽为3的矩形铁丝框变形为以为圆心,为半径的扇形(忽略铁丝的粗细),则所得扇形的面积为
A.
B.18
C.9
D.
【解答】解:矩形的长为6,宽为3,
,,
弧的弧长,
.
故选:.
7.(3分)一张正方形的纸片,剪去两个一样的小矩形得到一个“”图案,如图所示,设小矩形的长和宽分别为,,剪去部分的面积为20,若,则与的函数图象是
A.
B.
C.
D.
【解答】解:是剪去的两个矩形,两个矩形的面积和为20,
,
是的反比例函数,
,
答案为.
故选:.
8.(3分)若点,,在反比例函数的图象上,则,,的大小关系是
A.
B.
C.
D.
【解答】解:,
在第四象限,随的增大而增大,
,
,
,
故选:.
9.(3分)一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球的个数,小刚向其中放入10个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子,不断重复,共摸球200次,其中40次摸到黑球,则可以估计盒中大约有白球
A.30个
B.35个
C.40个
D.50个
【解答】解:设盒子里有白球个,
根据得:
解得:.
故选:.
10.(3分)如图,的半径弦于点,连接并延长交于点,连接.若,,则的长为
A.
B.
C.
D.8
【解答】解:连接,
设半径为,则,,
,
,
,
在中,由勾股定理得:,
,
,
为的直径,
,
由勾股定理得:,
在中,.
故选:.
11.(3分)如图,的外切正六边形的边长为2,则图中阴影部分的面积为
A.
B.
C.
D.
【解答】解:六边形是正六边形,
,
是等边三角形,,
设点为与的切点,连接,则,
,
.
故选:.
12.(3分)如图,从一张腰长为,顶角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为
A.
B.
C.
D.
【解答】解:过作于,,,
,
,
弧的长,
设圆锥的底面圆的半径为,则,解得.
故选:.
13.(3分)如图,的顶点在反比例函数的图象上,顶点在轴上,轴,若点的坐标为,,则的值为
A.4
B.
C.7
D.
【解答】解:轴,若点的坐标为,
设点
点,
点在反比例函数的图象上,
故选:.
二、填空题(每题3分,共12分)
14.(3分)在不透明的袋中装有除颜色外其它都相同的3个红球和2个白球,搅匀后从中随机摸出2个球,则摸出的两个球恰好一红一白的概率是 .
【解答】解:列表如下:
红
红
红
白
白
红
(红,红)
(红,红)
(红,白)
(红,白)
红
(红,红)
(红,红)
(红,白)
(红,白)
红
(红,红)
(红,红)
(红,白)
(红,白)
白
(白,红)
(白,红)
(白,红)
(白,白)
白
(白,红)
(白,红)
(白,红)
(白,白)
由树状图知,共有20种等可能结果,其中摸出的两个球恰好一红一白的有12种结果,
摸出的两个球恰好一红一白的概率为,
故答案为:.
15.(3分)如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,以为边在第一象限作正方形,点恰好在双曲线上,则值为 4 .
【解答】解:作轴于点.
在中,令,解得:,即的坐标是.
令,解得:,即的坐标是.
则,.
,
,
又中,,
,
在和中,
,
,
,,
故的坐标是,
代入得:,
故答案为:4.
16.(3分)如图,已知的半径为2,圆心在抛物线上运动,当与轴相切时,圆心的坐标为 ,或,或 .
【解答】解:与轴相切,点到轴的距离为2,即,
当时,,
解得:;
当时,,
解得:;
故圆心的坐标为:,或,或.
故答案为:,或,或.
17.(3分)如图,在中,,,,则的外心和内心之间的距离为 .
【解答】解:设的内切圆,为的外接圆的圆心,过点作于,于,于,
在中,,,,
,
点为的外心,
为外接圆半径,,
设的半径为,则,
又,
四边形是正方形,
,,,
,
解得:,
,,
在中,,,
,
故答案为:.
三、解答题(共49分)
18.(11分)四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
(1)随机抽取一张卡片,求恰好抽到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则如图所示.你认为这个游戏公平吗?请说明理由.
【解答】解:(1)(抽到数字.(2分)
(2)公平.
列表:
2
2
3
6
2
2
3
6
由上表可以看出,可能出现的结果共有16种,它们出现的可能性相同,所有的结果中,满足两位数不超过30的结果有8种.(5分)
所以(小贝胜),(小晶胜).所以游戏公平.(7分)
19.(12分)在平面直角坐标系中,直线与双曲线相交于点.
(1)求反比例函数的表达式;
(2)画出双曲线的示意图;
(3)若另一个交点的坐标为,则 ;当时,的取值范围为
;
(4)观察反比例函数的图象,当时,自变量的取值范围是
.
【解答】解:(1)直线与双曲线相交于点,
,
.
,
把代入,
,
反比例函数的表达式为;
(2)双曲线的示意图如图所示:
(3)直线与双曲线相交于另一个交点的坐标为,
,
,
,
由图象可知:当时,的取值范围或,
故答案为,或.
(4)观察图象,当时,自变量的取值范围是或,
故答案为或.
20.(12分)如图,已知在中,,,延长到,使,以为圆心,长为半径作交延长线于点,连接.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积.
【解答】(1)证明:连接,
,,
,
,
是等边三角形,
,,
,
,
即,
为半径,
是的切线;
(2)解:,,,
,
由勾股定理得:,
.
21.(14分)如图,已知在平面直角坐标系中,矩形的边轴,轴,点的坐标位,,.
(1)求直线的解析式;
(2)已知双曲线与折线的交点为,与折线的交点为.
①连接,当时,求该双曲线的解析式,并求出此时点的坐标;
②若双曲线与矩形各边和对角线的交点个数为3,请直接写出的取值范围.
【解答】解:(1),,,
,.
设直线的解析式为,
将,分别代人,
得,解得,
故直线的解析式为;
(2)①当时,,
,
,
又,
.
将点代人,
,
故该双曲线的解析式为,
将代人,得,
;
②或,
当双曲线经过点,即时,有2个交点;
当线经过点,即时,有3个交点,
故当时,有3个交点,
当双曲线与直线相切时,有3个交点,令,整理得,
当△时,双曲线与直线相切,此时,
或.
同课章节目录
