2021-2022学年苏科版七年级数学上册5.3 展开与折叠 课件(38张ppt)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学上册5.3 展开与折叠 课件(38张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 830.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 13:38:27 | ||
图片预览




文档简介
(共38张PPT)
5.3展开与折叠(一)
小壁虎的难题:
如图:一只圆桶的下方有一只壁虎,上方有一只蚊子,壁虎要想尽快吃到蚊子,应该走哪条路径?
你有何高招?
●
蚊子
壁虎
●
我们一起动动手:
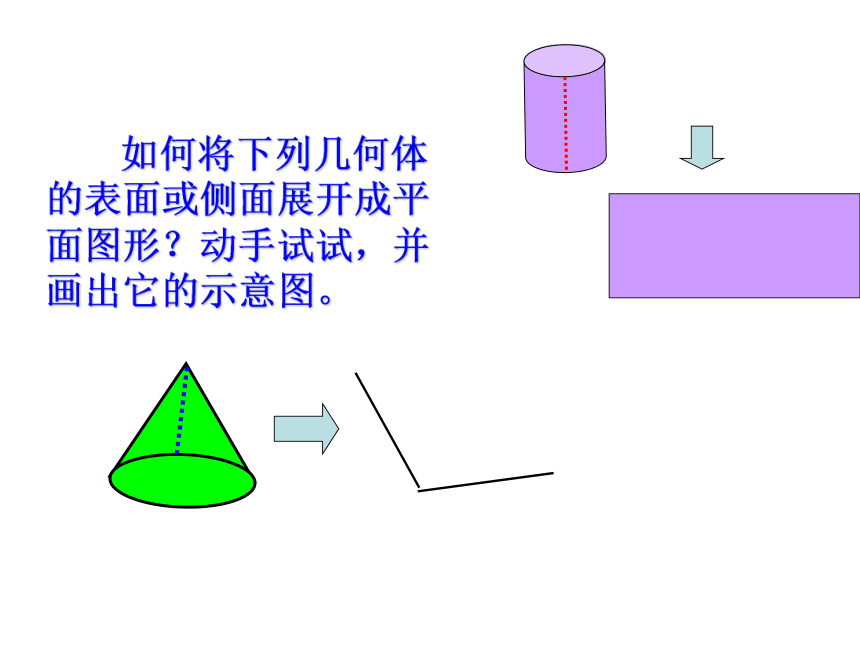
如何将下列几何体的表面或侧面展开成平面图形?动手试试,并画出它的示意图。
蚊子
●
●
壁虎
●
蚊子
壁虎
●
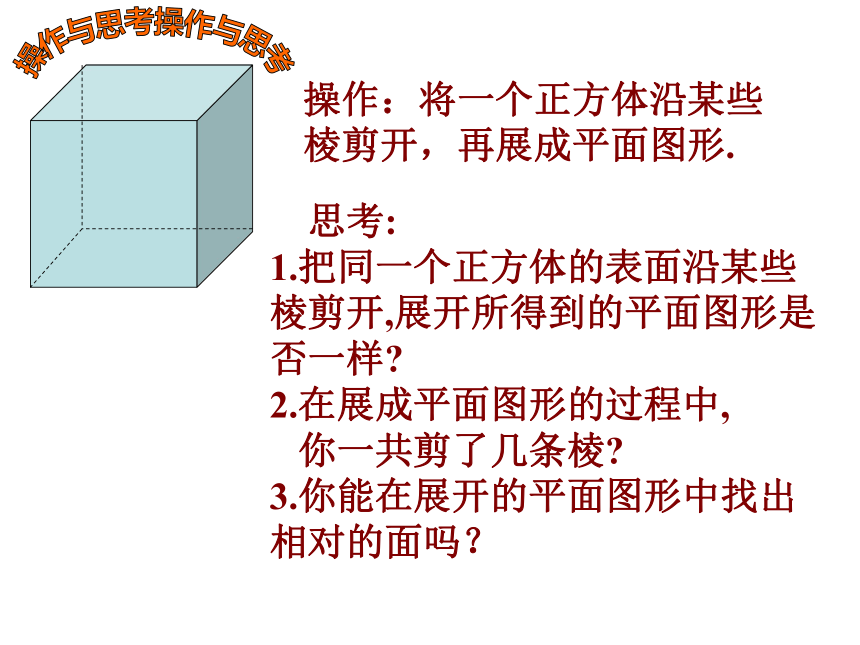
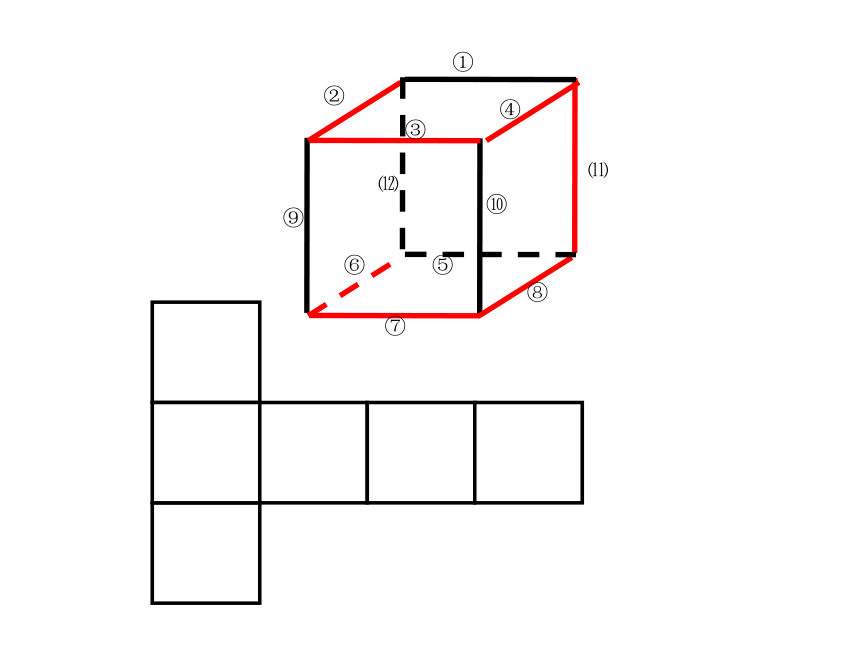
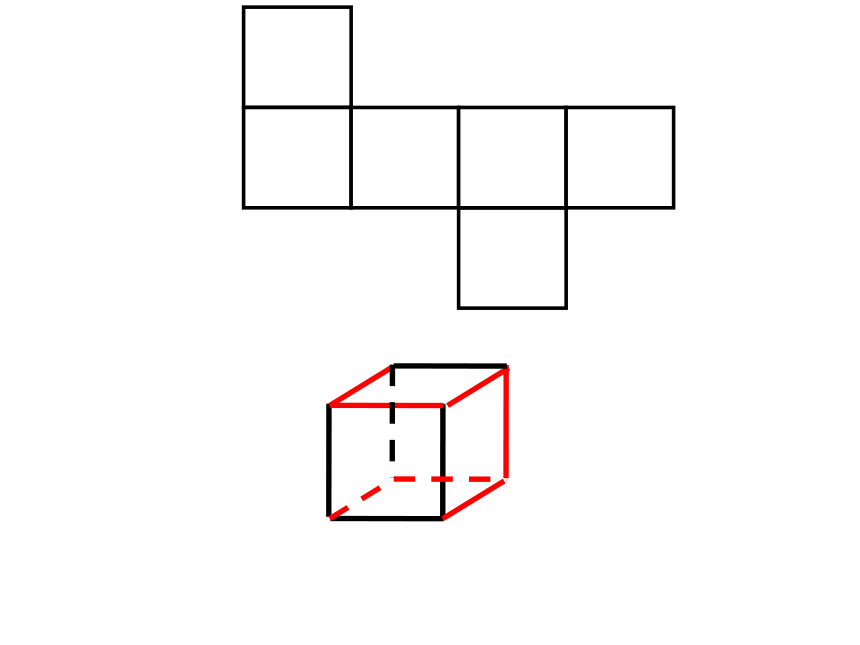
操作:将一个正方体沿某些
棱剪开,再展成平面图形.
思考:
1.把同一个正方体的表面沿某些棱剪开,展开所得到的平面图形是否一样?
2.在展成平面图形的过程中,
你一共剪了几条棱?
3.你能在展开的平面图形中找出相对的面吗?
操作与思考
①
②
③
④
⑤
⑥
⑧
⑦
⑨
⑩
⑾
⑿
第一类,1,4,
1型,共六种。
思考1
正方体展开所得到的平面图形有11种
第二类,2,3,1型,共三种。
第三类,2,2,2型,只有一种。
第四类,3,3型,只有一种。
一度测试
下列的图形都是正方体的展开图吗?
(5)
(2)
(6)
(3)
(1)
(4)
(√)
(√)
(√)
(×)
(×)
(√)
2、如图,哪一个是棱锥
侧面展开图?
(1)
(2)
(3)
√
3、如图,第一行的几何体表面展开后得到的第二行的某个平面图形,请用线连一连。
1
2
3
4
5
A
B
C
D
E
①
②
③
④
⑤
思考2:要将一个正方体纸盒的表面展开成一个平面图形,要剪开多少条棱?
思考3:
将相对的两个面涂上相同的颜色,正方体的平面展开图共有以下11种:
正方体的表面展开图用“口诀”:
一线不过四,
田凹应弃之;
相间、“Z”端是对面,
间二、拐角邻面知。
总结规律:
一线不过四
×
×
田凹应弃之
×
×
×
×
相间、“Z”端是对面
A
B
A
B
A和B为相对的两个面
间二、拐角邻面知
C
C
D
D
C和D为相邻的两个面
有一只虫子在正方体的一个顶点A,要爬到距它最远的另一个顶点B去,哪条路径最短?
B
●
●
A
拓展提高
展开
?
B
A
这样的路径有几条?
A
B
图(1)
图(2)
图(3)
图(4)
图(5)
图(6)
不是
不是
是
不是
不是
不是
二度测试
1.下列哪些是正方体的展开图?
你
太
棒
了
!
们
棒
KEY:
2、如果“你”在前面,那么谁在后面?
利
胜
持
是
就
坚
3、“坚”在下,“就”在后,胜、利在哪里?
“胜”在上,
“利”在前!
4.在图(1)~(4)的四个展开图中,哪一个
是(5)的展开图?
(1)
(2)
(3)
(4)
(5)
这节课你最大
的收获是什么
小结:
(1)正方体的展开图是平面图形;
(2)正方体的展开图,因展开方式的不同而不同,共有11种。
是不是所有的立体图形展开后,都是平面图形?
球体的展开图是不是平面图形?
NO!
交流归纳:
有些立体图形
展开
平面图形
有些平面图形
折叠
立体图形
5.3展开与折叠(一)
小壁虎的难题:
如图:一只圆桶的下方有一只壁虎,上方有一只蚊子,壁虎要想尽快吃到蚊子,应该走哪条路径?
你有何高招?
●
蚊子
壁虎
●
我们一起动动手:
如何将下列几何体的表面或侧面展开成平面图形?动手试试,并画出它的示意图。
蚊子
●
●
壁虎
●
蚊子
壁虎
●
操作:将一个正方体沿某些
棱剪开,再展成平面图形.
思考:
1.把同一个正方体的表面沿某些棱剪开,展开所得到的平面图形是否一样?
2.在展成平面图形的过程中,
你一共剪了几条棱?
3.你能在展开的平面图形中找出相对的面吗?
操作与思考
①
②
③
④
⑤
⑥
⑧
⑦
⑨
⑩
⑾
⑿
第一类,1,4,
1型,共六种。
思考1
正方体展开所得到的平面图形有11种
第二类,2,3,1型,共三种。
第三类,2,2,2型,只有一种。
第四类,3,3型,只有一种。
一度测试
下列的图形都是正方体的展开图吗?
(5)
(2)
(6)
(3)
(1)
(4)
(√)
(√)
(√)
(×)
(×)
(√)
2、如图,哪一个是棱锥
侧面展开图?
(1)
(2)
(3)
√
3、如图,第一行的几何体表面展开后得到的第二行的某个平面图形,请用线连一连。
1
2
3
4
5
A
B
C
D
E
①
②
③
④
⑤
思考2:要将一个正方体纸盒的表面展开成一个平面图形,要剪开多少条棱?
思考3:
将相对的两个面涂上相同的颜色,正方体的平面展开图共有以下11种:
正方体的表面展开图用“口诀”:
一线不过四,
田凹应弃之;
相间、“Z”端是对面,
间二、拐角邻面知。
总结规律:
一线不过四
×
×
田凹应弃之
×
×
×
×
相间、“Z”端是对面
A
B
A
B
A和B为相对的两个面
间二、拐角邻面知
C
C
D
D
C和D为相邻的两个面
有一只虫子在正方体的一个顶点A,要爬到距它最远的另一个顶点B去,哪条路径最短?
B
●
●
A
拓展提高
展开
?
B
A
这样的路径有几条?
A
B
图(1)
图(2)
图(3)
图(4)
图(5)
图(6)
不是
不是
是
不是
不是
不是
二度测试
1.下列哪些是正方体的展开图?
你
太
棒
了
!
们
棒
KEY:
2、如果“你”在前面,那么谁在后面?
利
胜
持
是
就
坚
3、“坚”在下,“就”在后,胜、利在哪里?
“胜”在上,
“利”在前!
4.在图(1)~(4)的四个展开图中,哪一个
是(5)的展开图?
(1)
(2)
(3)
(4)
(5)
这节课你最大
的收获是什么
小结:
(1)正方体的展开图是平面图形;
(2)正方体的展开图,因展开方式的不同而不同,共有11种。
是不是所有的立体图形展开后,都是平面图形?
球体的展开图是不是平面图形?
NO!
交流归纳:
有些立体图形
展开
平面图形
有些平面图形
折叠
立体图形
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
