27.2.1相似三角形的判定(第4课时) 课件(共30张PPPT)
文档属性
| 名称 | 27.2.1相似三角形的判定(第4课时) 课件(共30张PPPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 06:27:05 | ||
图片预览





文档简介
(共30张PPT)
27.2.1相似三角形的判定
---第4课时
人教版
九年级下
教学目标
1.
探索两角分别相等的两个三角形相似的判定定理.
2.
掌握利用两角分别相等来判定两个三角形相似的方法,并能
进行相关计算.(重点、难点)
3.
掌握判定两个直角三角形相似的方法,并能进行相关计算.
回顾旧知
1、想一想:
到目前为止我们学习了几种相似三角形的判定方法?
符号语言:
∵
DE∥BC
∴
△
ADE
∽
△
ABC
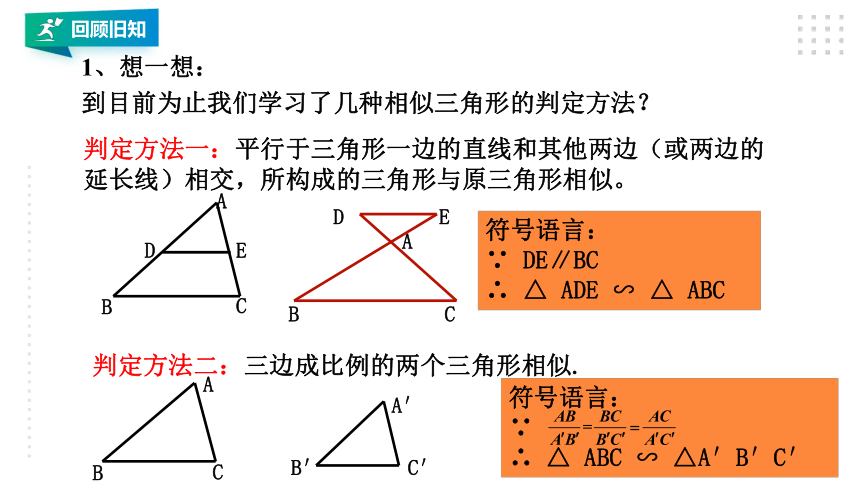
判定方法一:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
D
E
A
B
C
A
B
C
D
E
判定方法二:三边成比例的两个三角形相似.
符号语言:
∵
∴
△
ABC
∽
△A′B′C′
A
B
C
A′
B′
C′
回顾旧知
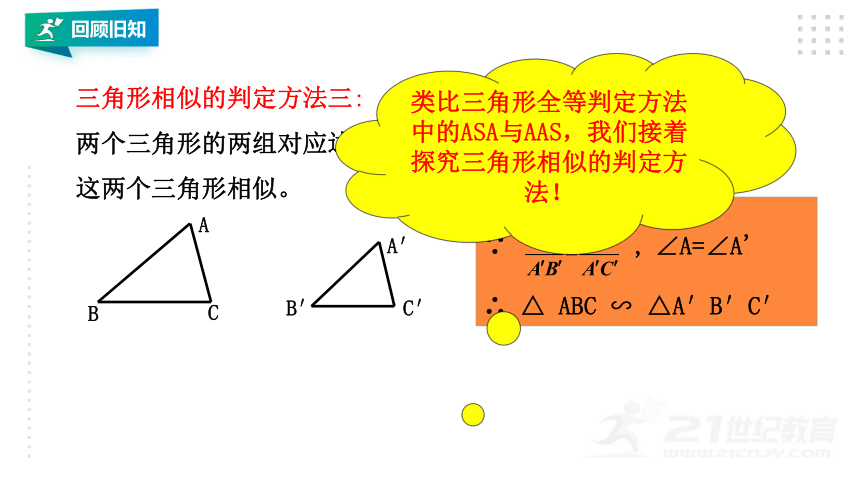
三角形相似的判定方法三:
两个三角形的两组对应边的比相等,且它们的夹角相等,那么这两个三角形相似。
A
B
C
A′
B′
C′
符号语言:
∵
,
∠A=∠A'
∴
△
ABC
∽
△A′B′C′
类比三角形全等判定方法中的ASA与AAS,我们接着探究三角形相似的判定方法!
合作探究
2、这两个三角形的三个内角的大小有什么关系?
3、三个内角对应相等的两个三角形一定相似吗?一定需要三个内角吗?我们一起探究!
三个内角对应相等。
观察与思考:1、你与老师的直角三角尺
,相似吗?
(30O
与60O)
相似!
合作探究
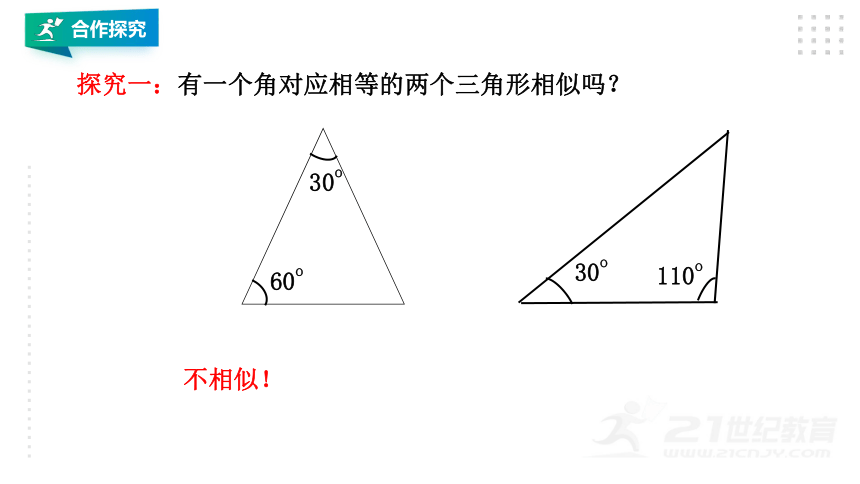
探究一:有一个角对应相等的两个三角形相似吗?
30o
30o
60o
110o
不相似!
合作探究
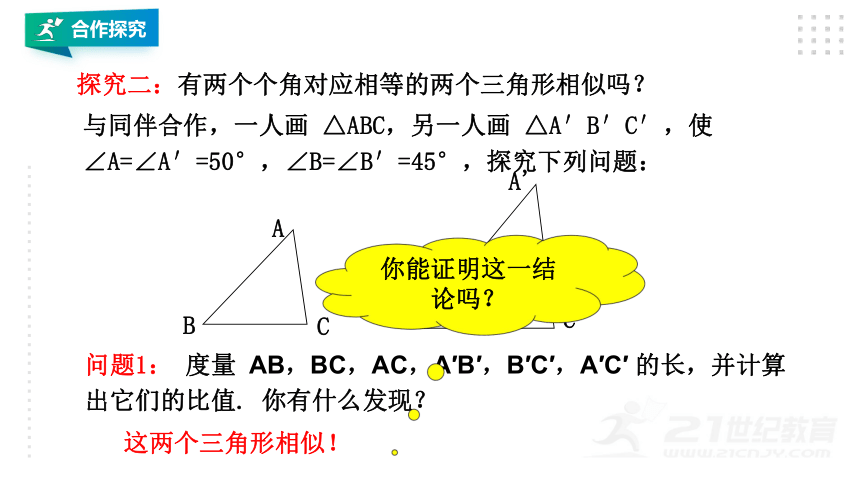
探究二:有两个个角对应相等的两个三角形相似吗?
问题1:
度量
AB,BC,AC,A′B′,B′C′,A′C′
的长,并计算出它们的比值.
你有什么发现?
C
A
B
A'
B'
C'
与同伴合作,一人画
△ABC,另一人画
△A′B′C′,使
∠A=∠A′=50°,∠B=∠B′=45°,探究下列问题:
这两个三角形相似!
你能证明这一结论吗?
合作探究
证明:在
△A′B′C′的边
A′B′上,
截取
A′D=AB,点
D
作
DE
//
B′C′,交
A′C′
于点
E,
则有△A′DE
∽△A′B′C′,∠A′DE
=∠B′.
∵∠B=∠B′,∴∠A′DE=∠B.
又∵
A′D=AB,∠A=∠A′,
∴△A′DE
≌△ABC,
∴△ABC∽△A′B′C′
.
C
A
A'
B
B'
C'
D
E
已知:在
△ABC与
△A′B′C′中,∠A=∠A′,∠B=∠B′;
求证:
△ABC∽△A′B′C′
合作探究
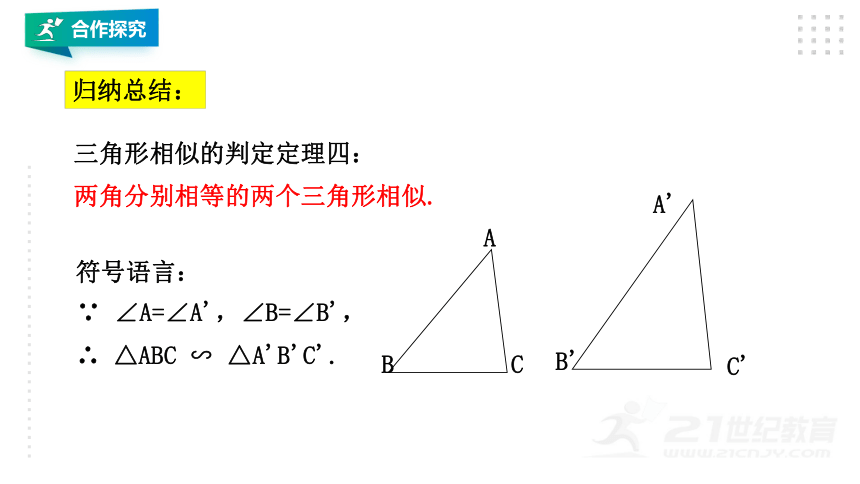
三角形相似的判定定理四:
两角分别相等的两个三角形相似.
∵
∠A=∠A',∠B=∠B',
∴
△ABC
∽
△A'B'C'.
符号语言:
归纳总结:
C
A
B
A'
B'
C'
趁热打铁
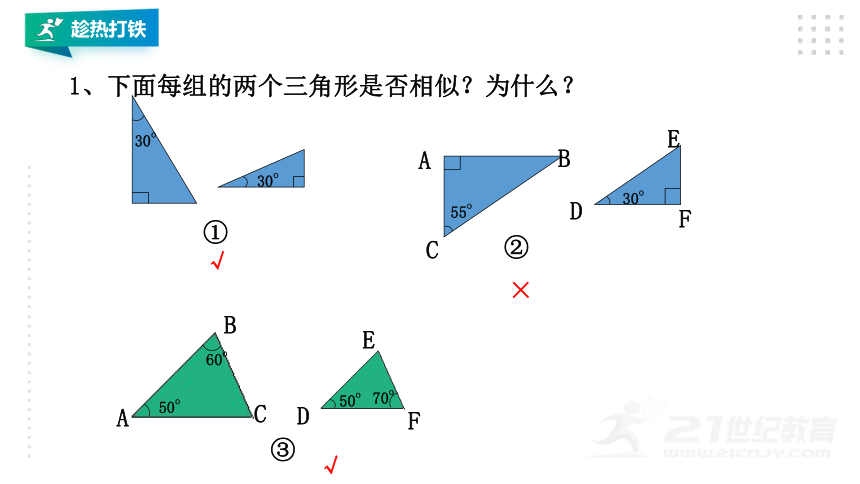
1、下面每组的两个三角形是否相似?为什么?
①
②
③
70o
50o
A
B
C
F
D
E
A
C
B
D
E
F
30o
30o
55o
30o
60o
50o
√
√
×
趁热打铁
2、如图,△ABC中,DE∥BC,EF∥AB,试说明△ADE∽△EFC.
A
E
F
B
C
D
解:
∵
DE∥BC,EF∥AB(已知),
∴
∠ADE=∠B=∠EFC
∠AED=∠C.
∴
△ADE∽△EFC.
典例精析
∴
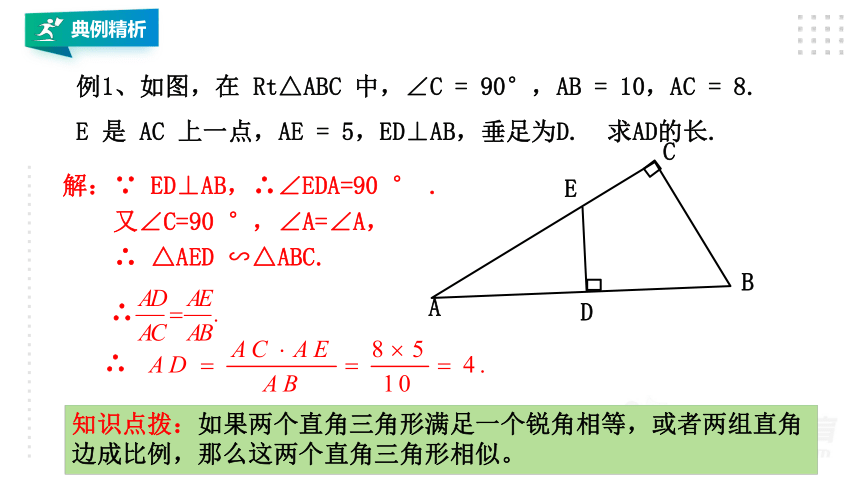
解:∵
ED⊥AB,∴∠EDA=90
°
.
又∠C=90
°,∠A=∠A,
∴
△AED
∽△ABC.
例1、如图,在
Rt△ABC
中,∠C
=
90°,AB
=
10,AC
=
8.
E
是
AC
上一点,AE
=
5,ED⊥AB,垂足为D.
求AD的长.
D
A
B
C
E
∴
知识点拨:如果两个直角三角形满足一个锐角相等,或者两组直角边成比例,那么这两个直角三角形相似。
合作探究
对于两个直角三角形,我们还可以用
“HL”判定它们全等.
那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
思考:
如图,在
Rt△ABC
和
Rt△A′B′C′
中,∠C=90°,∠C′=90°,
.
求证:Rt△ABC
∽
Rt△A′B′C′.
C
A
A'
B
B'
C'
分析:我们只需证明:
即可。
合作探究
证明:设____________=
k
,则AB=kA′B′,AC=kA′C′.
由
,得
∴
∴
Rt
△ABC
∽
Rt
△A′B′C′.
勾股定理
∴
C
A
A'
B
B'
C'
合作探究
直角三角形相似的判定方法:
斜边和一直角边成比例的两个直角三角形相似.
归纳总结:
在
Rt△ABC
和
Rt△A′B′C′
中,
∴
Rt
△ABC
∽
Rt
△A′B′C′.
符号语言:
C
A
A'
B
B'
C'
趁热打铁
证明:
∵
△ABC
的高AD、BE交于点F,
∴
∠FEA=∠FDB=90°,
∵∠AFE
=∠BFD
(对顶角相等).
∴
△FEA
∽
△
FDB,
∴
3.
如图,△ABC
的高
AD,BE
交于点
F.
求证:
D
C
A
B
E
F
综合演练
如图,已知
AB∥DE,∠AFC
=∠E,则图中相似三角形共有
(
)
A.
1对
B.
2对
C.
3对
D.
4对
C
2.
如图,△ABC中,AE
交
BC
于点
D,∠C=∠E,AD
:
DE=2
:3,
BD=6,则BC的长等于
(
)
A.4
B.6
C.8
D.10
D
C
A
B
D
E
综合演练
A
B
D
C
3.
如图,点
D
在
AB上,当∠
=∠
(或
∠
=∠
)时,
△ACD∽△ABC;
ACD
ACB
B
ADC
4.如图,⊙O
的弦
AB,CD
相交于点
P,
若
PA=4,PB
=
10,PC
=
5,则
PD
=
.
8
O
D
C
B
A
P
知识点拨:题中涉及的线段属于△BCP和△ADP,因此连接AD、BC,根据圆周角的性质得到解题所需角度,进而求解。
综合演练
证明:
∵∠BAC=
∠1+
∠DAC,
∠DAE=
∠3+
∠DAC,∠1=∠3,
∴
∠BAC=∠DAE.
∵
∠C=180°-∠2-∠DOC
,
∠E=180°-∠3-∠AOE,
∠DOC
=∠AOE(对顶角相等),
∴
∠C=
∠E.
∴
△ABC∽△ADE.
5.
如图,∠1=∠2=∠3,求证:△ABC
∽△ADE.
A
B
C
D
E
1
3
2
O
综合演练
6、如图,弦
AB
和
CD
相交于
⊙O
内一点
P,求证:PA
·
PB=
PC
·
PD.
证明:连接AC,DB.
∵∠A
和
∠D
都是弧
CB
所对的圆周角,
∴
∠A=
,
同理
∠C=
,
∴
△PAC
∽
△PDB,
∴
即PA
·PB
=
PC
·
PD.
∠D
∠B
O
D
C
B
A
P
综合演练
7、如图,在矩形ABCD中,AC是对角线,E是AC的中点,过E作MN交AD于M,交BC于N,若CEN=90°,EN:AB=2:3,EC=3,求BC的长。
解:∵
∠CEN=90°∠ACB=∠NCE
∴
△ABC
∽
△NEC,
∴
又∵EC=3
∴BC=4.5
综合演练
8、已知,如图,梯形ABCD中,AD∥BC,
∠A=900,对角线BD⊥CD;
求证:(1)
△ABD∽△DCB;
(2)BD2=AD·BC
A
B
C
D
证明:(1)
∵AD∥BC,
∴
∠ADB=
∠DBC
∵
∠A=∠BDC=
90°,
∴
△ABD∽△DCB
(2)
∵
△ABD∽△DCB
∴
AD
BD
BD
BC
即:BD2=AD·BC
=
综合演练
9、如图,已知:∠ACB
=∠ADC
=
90°,AD
=
2,CD
=
,当
AB
的长为多长时,△ACB
与△ADC相似.
C
A
B
D
解:∵∠ADC
=
90°,AD
=
2,CD
=
,
要使这两个直角三角形相似,有两种情况:
当
Rt△ABC
∽
Rt△ACD
时,
有
AC
:
AD
=AB
:
AC,
即
:
2
=AB
:
,
解得
AB=3;
∴
C
A
B
D
(2)
当
Rt△ACB
∽
Rt△CDA
时,
有
AC
:
CD
=AB
:
AC
,
即
:
=AB
:
,
解得
AB=
.
∴
当
AB
的长为
3
或
时,这两个直
角三角形相似.
综合演练
提能训练
10、如图,Rt△ABC中,CD是斜边上的高,
△ADC和△CBD和△ABC相似吗?证明你的结论。在图中的已有线段之间有哪些等量关系?
课堂总结
说一说
1、你学习了判定三角形相似的哪个方法?
2、判定两个直角三角形相似有哪些方法?
本节课你有哪些收获?
作业布置
习题27.2
P42页:2(2)、7
https://www.21cnjy.com/help/help_extract.php
27.2.1相似三角形的判定
---第4课时
人教版
九年级下
教学目标
1.
探索两角分别相等的两个三角形相似的判定定理.
2.
掌握利用两角分别相等来判定两个三角形相似的方法,并能
进行相关计算.(重点、难点)
3.
掌握判定两个直角三角形相似的方法,并能进行相关计算.
回顾旧知
1、想一想:
到目前为止我们学习了几种相似三角形的判定方法?
符号语言:
∵
DE∥BC
∴
△
ADE
∽
△
ABC
判定方法一:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
D
E
A
B
C
A
B
C
D
E
判定方法二:三边成比例的两个三角形相似.
符号语言:
∵
∴
△
ABC
∽
△A′B′C′
A
B
C
A′
B′
C′
回顾旧知
三角形相似的判定方法三:
两个三角形的两组对应边的比相等,且它们的夹角相等,那么这两个三角形相似。
A
B
C
A′
B′
C′
符号语言:
∵
,
∠A=∠A'
∴
△
ABC
∽
△A′B′C′
类比三角形全等判定方法中的ASA与AAS,我们接着探究三角形相似的判定方法!
合作探究
2、这两个三角形的三个内角的大小有什么关系?
3、三个内角对应相等的两个三角形一定相似吗?一定需要三个内角吗?我们一起探究!
三个内角对应相等。
观察与思考:1、你与老师的直角三角尺
,相似吗?
(30O
与60O)
相似!
合作探究
探究一:有一个角对应相等的两个三角形相似吗?
30o
30o
60o
110o
不相似!
合作探究
探究二:有两个个角对应相等的两个三角形相似吗?
问题1:
度量
AB,BC,AC,A′B′,B′C′,A′C′
的长,并计算出它们的比值.
你有什么发现?
C
A
B
A'
B'
C'
与同伴合作,一人画
△ABC,另一人画
△A′B′C′,使
∠A=∠A′=50°,∠B=∠B′=45°,探究下列问题:
这两个三角形相似!
你能证明这一结论吗?
合作探究
证明:在
△A′B′C′的边
A′B′上,
截取
A′D=AB,点
D
作
DE
//
B′C′,交
A′C′
于点
E,
则有△A′DE
∽△A′B′C′,∠A′DE
=∠B′.
∵∠B=∠B′,∴∠A′DE=∠B.
又∵
A′D=AB,∠A=∠A′,
∴△A′DE
≌△ABC,
∴△ABC∽△A′B′C′
.
C
A
A'
B
B'
C'
D
E
已知:在
△ABC与
△A′B′C′中,∠A=∠A′,∠B=∠B′;
求证:
△ABC∽△A′B′C′
合作探究
三角形相似的判定定理四:
两角分别相等的两个三角形相似.
∵
∠A=∠A',∠B=∠B',
∴
△ABC
∽
△A'B'C'.
符号语言:
归纳总结:
C
A
B
A'
B'
C'
趁热打铁
1、下面每组的两个三角形是否相似?为什么?
①
②
③
70o
50o
A
B
C
F
D
E
A
C
B
D
E
F
30o
30o
55o
30o
60o
50o
√
√
×
趁热打铁
2、如图,△ABC中,DE∥BC,EF∥AB,试说明△ADE∽△EFC.
A
E
F
B
C
D
解:
∵
DE∥BC,EF∥AB(已知),
∴
∠ADE=∠B=∠EFC
∠AED=∠C.
∴
△ADE∽△EFC.
典例精析
∴
解:∵
ED⊥AB,∴∠EDA=90
°
.
又∠C=90
°,∠A=∠A,
∴
△AED
∽△ABC.
例1、如图,在
Rt△ABC
中,∠C
=
90°,AB
=
10,AC
=
8.
E
是
AC
上一点,AE
=
5,ED⊥AB,垂足为D.
求AD的长.
D
A
B
C
E
∴
知识点拨:如果两个直角三角形满足一个锐角相等,或者两组直角边成比例,那么这两个直角三角形相似。
合作探究
对于两个直角三角形,我们还可以用
“HL”判定它们全等.
那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
思考:
如图,在
Rt△ABC
和
Rt△A′B′C′
中,∠C=90°,∠C′=90°,
.
求证:Rt△ABC
∽
Rt△A′B′C′.
C
A
A'
B
B'
C'
分析:我们只需证明:
即可。
合作探究
证明:设____________=
k
,则AB=kA′B′,AC=kA′C′.
由
,得
∴
∴
Rt
△ABC
∽
Rt
△A′B′C′.
勾股定理
∴
C
A
A'
B
B'
C'
合作探究
直角三角形相似的判定方法:
斜边和一直角边成比例的两个直角三角形相似.
归纳总结:
在
Rt△ABC
和
Rt△A′B′C′
中,
∴
Rt
△ABC
∽
Rt
△A′B′C′.
符号语言:
C
A
A'
B
B'
C'
趁热打铁
证明:
∵
△ABC
的高AD、BE交于点F,
∴
∠FEA=∠FDB=90°,
∵∠AFE
=∠BFD
(对顶角相等).
∴
△FEA
∽
△
FDB,
∴
3.
如图,△ABC
的高
AD,BE
交于点
F.
求证:
D
C
A
B
E
F
综合演练
如图,已知
AB∥DE,∠AFC
=∠E,则图中相似三角形共有
(
)
A.
1对
B.
2对
C.
3对
D.
4对
C
2.
如图,△ABC中,AE
交
BC
于点
D,∠C=∠E,AD
:
DE=2
:3,
BD=6,则BC的长等于
(
)
A.4
B.6
C.8
D.10
D
C
A
B
D
E
综合演练
A
B
D
C
3.
如图,点
D
在
AB上,当∠
=∠
(或
∠
=∠
)时,
△ACD∽△ABC;
ACD
ACB
B
ADC
4.如图,⊙O
的弦
AB,CD
相交于点
P,
若
PA=4,PB
=
10,PC
=
5,则
PD
=
.
8
O
D
C
B
A
P
知识点拨:题中涉及的线段属于△BCP和△ADP,因此连接AD、BC,根据圆周角的性质得到解题所需角度,进而求解。
综合演练
证明:
∵∠BAC=
∠1+
∠DAC,
∠DAE=
∠3+
∠DAC,∠1=∠3,
∴
∠BAC=∠DAE.
∵
∠C=180°-∠2-∠DOC
,
∠E=180°-∠3-∠AOE,
∠DOC
=∠AOE(对顶角相等),
∴
∠C=
∠E.
∴
△ABC∽△ADE.
5.
如图,∠1=∠2=∠3,求证:△ABC
∽△ADE.
A
B
C
D
E
1
3
2
O
综合演练
6、如图,弦
AB
和
CD
相交于
⊙O
内一点
P,求证:PA
·
PB=
PC
·
PD.
证明:连接AC,DB.
∵∠A
和
∠D
都是弧
CB
所对的圆周角,
∴
∠A=
,
同理
∠C=
,
∴
△PAC
∽
△PDB,
∴
即PA
·PB
=
PC
·
PD.
∠D
∠B
O
D
C
B
A
P
综合演练
7、如图,在矩形ABCD中,AC是对角线,E是AC的中点,过E作MN交AD于M,交BC于N,若CEN=90°,EN:AB=2:3,EC=3,求BC的长。
解:∵
∠CEN=90°∠ACB=∠NCE
∴
△ABC
∽
△NEC,
∴
又∵EC=3
∴BC=4.5
综合演练
8、已知,如图,梯形ABCD中,AD∥BC,
∠A=900,对角线BD⊥CD;
求证:(1)
△ABD∽△DCB;
(2)BD2=AD·BC
A
B
C
D
证明:(1)
∵AD∥BC,
∴
∠ADB=
∠DBC
∵
∠A=∠BDC=
90°,
∴
△ABD∽△DCB
(2)
∵
△ABD∽△DCB
∴
AD
BD
BD
BC
即:BD2=AD·BC
=
综合演练
9、如图,已知:∠ACB
=∠ADC
=
90°,AD
=
2,CD
=
,当
AB
的长为多长时,△ACB
与△ADC相似.
C
A
B
D
解:∵∠ADC
=
90°,AD
=
2,CD
=
,
要使这两个直角三角形相似,有两种情况:
当
Rt△ABC
∽
Rt△ACD
时,
有
AC
:
AD
=AB
:
AC,
即
:
2
=AB
:
,
解得
AB=3;
∴
C
A
B
D
(2)
当
Rt△ACB
∽
Rt△CDA
时,
有
AC
:
CD
=AB
:
AC
,
即
:
=AB
:
,
解得
AB=
.
∴
当
AB
的长为
3
或
时,这两个直
角三角形相似.
综合演练
提能训练
10、如图,Rt△ABC中,CD是斜边上的高,
△ADC和△CBD和△ABC相似吗?证明你的结论。在图中的已有线段之间有哪些等量关系?
课堂总结
说一说
1、你学习了判定三角形相似的哪个方法?
2、判定两个直角三角形相似有哪些方法?
本节课你有哪些收获?
作业布置
习题27.2
P42页:2(2)、7
https://www.21cnjy.com/help/help_extract.php
