安徽省滁州市定远民族高级中学校2021-2022学年高二上学期期初质量检测数学试题(Word版含答案)
文档属性
| 名称 | 安徽省滁州市定远民族高级中学校2021-2022学年高二上学期期初质量检测数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 92.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 08:02:49 | ||
图片预览



文档简介
定远民族高中2021—2022学年度第一学期初期高二质量检测
数学试卷
一、选择题(共12小题,每小题5分,共60分)
1.已知复数z1=2+i,z2在复平面内对应的点在直线x=1上,且满足1·z2是实数,则z2等于( )
A.
1-i
B.
1+i
C.+i
D.-i
2.已知空间向量a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|等于(
)
A.
B.
C.
D.
3.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F.若=a,=b,则等于( )
A.a+b
B.a+b
C.a+b
D.a+b
4.在△ABC中,点D在直线CB的延长线上,且=4=r+s,
则r-s等于( )
A.
0
B.
C.
D.
3
5.某公司有一批专业技术人员,其中年龄在35~50岁的本科生和研究生分别有30人和20人,现用分层抽样法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体,从中任意抽取3人,则至少有1人为研究生的概率为( )
A.
B.
C.
D.
6.已知A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
A.
等腰三角形
B.
等边三角形C.
直角三角形
D.
等腰直角三角形
7.梯形OABC的直观图是一个等腰梯形O′A′B′C′,等腰梯形O′A′B′C′的底角为45°,且面积为,则梯形ABCD的面积为( )
A.
4
B.
2
C.
2
D.
8.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意程度越高,现随机抽取6位小区居民,他们的“幸福感指数”分别为5,6,7,8,9,5,则这组数据第80百分位数是( )
A.7 B.7.5
C.8 D.9
9.甲从正方形四个顶点中任选两个顶点连成直线,乙也从该正方形四个顶点中任选两个顶点连成直线,则所得的两条直线相互垂直的概率是( )
A.
B.
C.
D.
10.《算数书》竹简于上世纪八十年代在湖北省张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“禾盖”的术:置如其周,令相乘也,又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈L2h相当于将圆锥体积公式中的圆周率π近似取为( )
A.
B.
C.
D.
11.设m,n是两条不同的直线,α,β,γ是三个不同的平面,下列命题中正确的是( )
A.
若m?β,α⊥β,则m⊥α
B.
若m∥α,m⊥β,则α⊥β
C.
若α⊥β,α⊥γ,则β⊥γ
D.
若α∩γ=m,β∩γ=n,m∥n,则α∥β
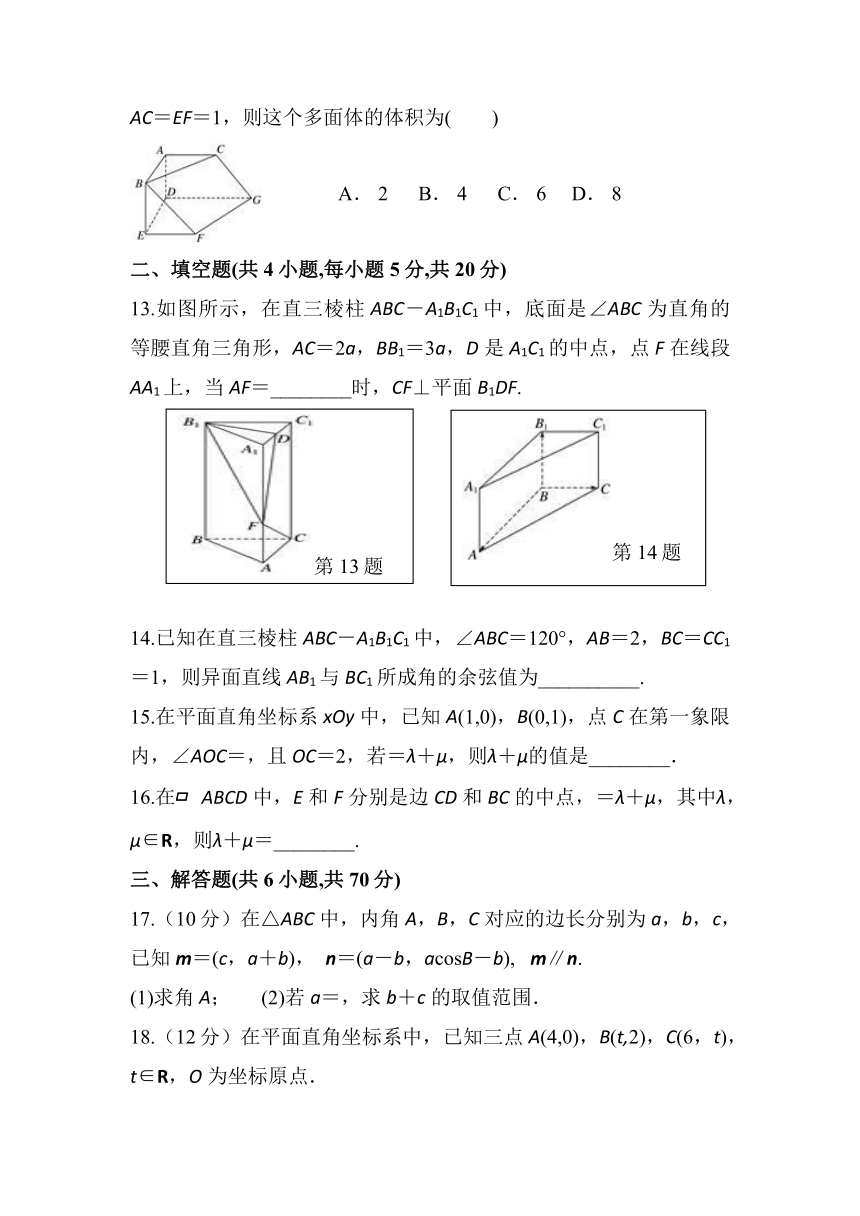
12.已知多面体ABC-DEFG中(如图),AB、AC、AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则这个多面体的体积为( )
A.
2
B.
4
C.
6
D.
8
二、填空题(共4小题,每小题5分,共20分)
(
第14题
)
(
第13题
)13.如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=________时,CF⊥平面B1DF.
14.已知在直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为__________.
15.在平面直角坐标系xOy中,已知A(1,0),B(0,1),点C在第一象限内,∠AOC=,且OC=2,若=λ+μ,则λ+μ的值是________.
16.在?ABCD中,E和F分别是边CD和BC的中点,=λ+μ,其中λ,μ∈R,则λ+μ=________.
三、解答题(共6小题,共70分)
17.(10分)在△ABC中,内角A,B,C对应的边长分别为a,b,c,已知m=(c,a+b),
n=(a-b,acosB-b),
m∥n.
(1)求角A;
(2)若a=,求b+c的取值范围.
18.(12分)在平面直角坐标系中,已知三点A(4,0),B(t,2),C(6,t),t∈R,O为坐标原点.
(1)若△ABC是直角三角形,求t的值;
(2)若四边形ABCD是平行四边形,求||的最小值.
(
第19题
)19.(12分)在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(1)求证:BD⊥平面AED;
(2)求二面角F-BD-C的余弦值.
20.(12分)在△ABC中,已知·=3·.
(1)求证:tanB=3tanA;
(2)若cosC=,求A的值.
21.(12分)已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)若点D在直线AC上,且⊥,求点D的坐标;
(2)求以BA,BC为邻边的平行四边形的面积.
22.(12分)如图所示,在矩形ABCD中,AB=2,AD=1,E为CD中点,以AE为折痕,把△DAE折起到△D′AE的位置,且平面D′AE⊥平面ABCE.
(1)求证:AD′⊥BE;
(2)求四棱锥D′-ABCE的体积;
(3)在棱ED′上是否存在一点P,使得D′B∥平面PAC,若存在,求出点P的位置,若不存在,请说明理由.
答案解析
1.【答案】B
【解析】由z1=2+i,得1=2-i,
由z2在复平面内对应的点在直线x=1上,
可设z2=1+bi(b∈R),
则1·z2=(2-i)·(1+bi)=2+b+(2b-1)i.
又1·z2为实数,所以2b-1=0,b=.
所以z2=1+i.
2.【答案】B
【解析】因为a=(1,n,2),b=(-2,1,2),
所以2a-b=(4,2n-1,2).
因为2a-b与b垂直,
所以(2a-b)·b=0,
所以-8+2n-1+4=0,
解得n=,所以a=,
所以|a|==.
3.【答案】B
【解析】如图所示,
∵E是OD的中点,∴==b.
又∵△ABE∽△FDE,∴==.
∴=3,∴=.
在△AOE中,=+=a+b,
∴==a+b,故选B.
4.【答案】C
【解析】∵=+=4,∴=3.
∴=-=+-=+-=+(-)-=-,
∴r=,s=-,r-s=,故选C.
5.【答案】D
【解析】设容量为5的样本中本科生的人数为m,由题意可得=,解得m=3,所以样本中有研究生2人,分别记为A,B,本科生3人,分别记为a,b,c,所以从中任意抽取3人的所有情况有(A,B,a),(A,B,b),(A,B,c),(A,a,b),(A,a,c),(A,b,c),(B,a,b),(B,a,c),(B,b,c),(a,b,c),共10种,3人均为本科生的情况只有(a,b,c)1种,所以至少有1人为研究生的概率为=.
6.【答案】C
【解析】因为=(3,4,-8),=(2,-3,1),=(5,1,-7),
·=10-3-7=0,∴BC⊥AC,
而||=,||=5,
所以△ABC是直角三角形.
7.【答案】A
【解析】如图,由斜二测画法原理知,平面中的图形与直观图中的图形上下底边的长度是一样的,不一样的是两个梯形的高,其高的关系是这样的:平面图中的高OA是直观图中O′A′长度的2倍,如直观图,O′A′的长度是直观图中梯形的高的倍,由此平面图中梯形的高OA的长度是直观图中梯形高的2×=2倍,故其面积是梯形O′A′B′C′的面积的2倍,
又∵梯形O′A′B′C′的面积为,
∴原梯形的面积是4.
故选A.
8.【答案】C [该组数据从小到大排列为5,5,6,7,8,9,且6×80%=4.8.所以这组数据的第80百分位数是8.]
9.【答案】C
【解析】甲从正方形四个顶点中任意选择两个顶点连成直线,乙也从正方形四个顶点中任意选择两个顶点连成直线,所得的直线共有6×6=36(对),而相互垂直的有10对,故根据古典概型概率公式得P==.
10.【答案】D
【解析】设圆锥的底面半径为r,则圆锥的底面周长L=2πr,∴r=,∴V=πr2h=.令=L2h,提π=,故选D.
11.【答案】B
【解析】若m?β,α⊥β,则m与α的关系不确定,故A错误;若m∥α,则存在直线n?α,使m∥n,又由m⊥β,可得n⊥β,进而由面面垂直的判定定理得到α⊥β,故B正确;若α⊥β,α⊥γ,则β与γ关系不确定,故C错误;若α∩γ=m,β∩γ=n,m∥n,则α与β可能平行,也可能相交(此时交线与m,n均平行),故D错误.故选B.
12.【答案】B
【解析】取DG中点M,连接CM,AM,FM,则这个多面体的体积可以表示为棱柱BEF-ADM与三棱锥C-FMG以及四棱锥C-ABFM的和.由于多面体ABC-DEFG中(如图),AB、AC、AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,故棱柱BEF-ADM可看作是底面是直角三角形的三棱柱,其高是2,底面是两直角边分别是1,2的三角形,其体积是2××2×1=2.三棱锥C-FMG以CM为高,其长为2,底面是以MF=2,MG=1为直角边的直角三角形,其体积为×2××2×1=.由图形知,C到AM的距离就是四棱锥C-ABFM的高,由于AM=,由等面积法可求得C到AM的距离是,底面四边形是以AM=与AB=2为边长的矩形,故其体积为××2×=.
所以这个多面体的体积为++2=4.
故选B.
13.
【答????案】
a或2a
【解????析】
由已知得B1D⊥AC1,
又CF?平面AC1,∴B1D⊥CF,
故若CF⊥平面B1DF,则必有CF⊥DF.
设AF=x(0<x<3a),则CF2=x2+4a2,
DF2=a2+(3a-x)2,又CD2=a2+9a2=10a2,
∴10a2=x2+4a2+a2+(3a-x)2,
解得x=a或2a.故答案为a或2a.
14.
【答????案】
【解????析】
如图所示,
设=a,=b,=c,则〈a,b〉=120°,c⊥a,c⊥b,
因为=+=-a+c,=+=b+c,
|cos〈,〉|===
===.
15.【答案】+1
【解析】由题意,知=(1,0),=(0,1).
设C(x,y),则=(x,y).
∵=λ+μ,
∴(x,y)=λ(1,0)+μ(0,1)=(λ,μ),
∴又∵∠AOC=,OC=2,
∴λ=x=2cos=,μ=y=2sin=1,
∴λ+μ=+1.
16.
【答????案】
43
【解????析】
设AB→=a,AD→=b,则AC→=a+b,AE→=12a+b,AF→=a+12b,
∴λAE→+μAF→=λ(12a+b)+μ(a+12b)=(12λ+μ)a+(λ+12μ)b,
∴a+b=(12λ+μ)a+(λ+12μ)b,
∴?,,12λ+μ=1,λ+12μ=1,∴,,λ=23,μ=23,∴λ+μ=43.
17.【答案】(1)∵c=a2-b2,由余弦定理
得a2+c2-b2-bc=2a2-2b2,a2=b2+c2-bc.
∵a2=b2+c2-2bccosA,∴cosA=,
∵A∈
(0,π),∴A=.
(2)由正弦定理得===2,
∴b=2sinB,c=2sinC,
∴b+c=2sinB+2sinC=2sinB+2sin
(A+B)
=2sinB+2sinAcosB+2cosAsinB
=2sinB+2×cosB+2×sinB
=3sinB+cosB
=2sin.
∵B∈,∴B+∈,
sin∈,
∴b+c∈.
(1)由题意得AB=(t-4,2),AC=(2,t),BC=(6-t,t-2),
若∠A=90°,则AB?AC=0,即2(t-4)+2t=0,∴t=2;
若∠B=90°,则AB?BC=0,即(t-4)(6-t)+2(t-2)=0,∴t=6±2;
若∠C=90°,则AC?BC=0,即2(6-t)+t(t-2)=0,无解,
∴满足条件的t的值为2或6±2.
(2)若四边形ABCD是平行四边形,则AD=BC,设D的坐标为(x,y),
即(x-4,y)=(6-t,t-2),∴x-4=6-t,y=t-2即D(10-t,t-2),
∴|OD|
2=(10-t)
2+(t-2)
2=2t
2-24t+104,
∴当t=6时,|OD|的最小值为4.
19.【答案】(1)证明 因为四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
所以∠ADC=∠BCD=120°.
又CB=CD,所以∠CDB=30°,
因此∠ADB=90°,即AD⊥BD.
又AE⊥BD,且AE∩AD=A,AE,AD?平面AED,
所以BD⊥平面AED.
(2)解 如图,
取BD的中点G,连接CG,FG,
由于CB=CD,
因此CG⊥BD.
又FC⊥平面ABCD,BD?平面ABCD,
所以FC⊥BD.
由于FC∩CG=C,FC,CG?平面FCG,
所以BD⊥平面FCG,
故BD⊥FG,
所以∠FGC为二面角F-BD-C的平面角.
在等腰三角形BCD中,由于∠BCD=120°,
因此CG=CB.又CB=CF,
所以GF==CG,
故cos∠FGC=,
因此二面角F-BD-C的余弦值为.
20.【答案】(1)证明 因为·=3·,
所以AB·AC·cosA=3BA·BC·cosB,
即AC·cosA=3BC·cosB.
由正弦定理知=,
从而sinBcosA=3sinAcosB.
又因为00,cosB>0,
所以tanB=3tanA.
(2)解 因为cosC=,0所以sinC==,
从而tanC=2,于是tan[π-(A+B)]=2,
即tan(A+B)=-2,
亦即=-2.
由(1)得=-2,
解得tanA=1或tanA=-.
因为cosA>0,所以tanA=1,所以A=.
21.【答案】解 (1)由题意知,=(1,-3,2),点D在直线AC上,
设=λ=λ(1,-3,2)=(λ,-3λ,2λ),
∴D(λ,2-3λ,2λ+3),
=(λ,2-3λ,3+2λ)-(-2,1,6)
=(λ+2,1-3λ,2λ-3),
∵⊥,
∴·=(1,-3,2)·(λ+2,1-3λ,2λ-3)
=λ+2-3+9λ+4λ-6=14λ-7=0,
∴λ=,
∴D.
(2)∵=(2,1,-3),=(3,-2,-1),
∴||==,
||==,
∴·=2×3+1×(-2)+(-3)×(-1)=7,
∴cosB=cos〈,〉===,
∴sinB=,
∴S=××=7,
∴以BA,BC为邻边的平行四边形的面积为7.
22.【答案】(1)证明 根据题意可知,在长方形ABCD中,△DAE和△CBE为等腰直角三角形,
∴∠DEA=∠CEB=45°,
∴∠AEB=90°,即BE⊥AE.
∵平面D′AE⊥平面ABCE,且平面D′AE∩平面ABCE=AE,BE?平面ABCE,
∴BE⊥平面D′AE,∵AD′?平面D′AE,
∴AD′⊥BE.
(2)解 取AE的中点F,连接D′F,则D′F⊥AE.
∵平面D′AE⊥平面ABCE,
且平面D′AE∩平面ABCE=AE,D′F?平面D′AE,
∴D′F⊥平面ABCE,
∴VD′-ABCE=S四边形ABCE·D′F=××(1+2)×1×=.
(3)解 如图所示,连接AC交BE于Q,假设在D′E上存在点P,使得D′B∥平面PAC,连接PQ.
∵D′B?平面D′BE,
平面D′BE∩平面PAC=PQ,∴D′B∥PQ,
∴在△EBD′中,=.
∵在梯形ABCE中,==,
∴==,即EP=ED′,
∴在棱ED′上存在一点P,且EP=ED′,使得D′B∥平面PAC.
数学试卷
一、选择题(共12小题,每小题5分,共60分)
1.已知复数z1=2+i,z2在复平面内对应的点在直线x=1上,且满足1·z2是实数,则z2等于( )
A.
1-i
B.
1+i
C.+i
D.-i
2.已知空间向量a=(1,n,2),b=(-2,1,2),若2a-b与b垂直,则|a|等于(
)
A.
B.
C.
D.
3.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F.若=a,=b,则等于( )
A.a+b
B.a+b
C.a+b
D.a+b
4.在△ABC中,点D在直线CB的延长线上,且=4=r+s,
则r-s等于( )
A.
0
B.
C.
D.
3
5.某公司有一批专业技术人员,其中年龄在35~50岁的本科生和研究生分别有30人和20人,现用分层抽样法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体,从中任意抽取3人,则至少有1人为研究生的概率为( )
A.
B.
C.
D.
6.已知A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
A.
等腰三角形
B.
等边三角形C.
直角三角形
D.
等腰直角三角形
7.梯形OABC的直观图是一个等腰梯形O′A′B′C′,等腰梯形O′A′B′C′的底角为45°,且面积为,则梯形ABCD的面积为( )
A.
4
B.
2
C.
2
D.
8.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意程度越高,现随机抽取6位小区居民,他们的“幸福感指数”分别为5,6,7,8,9,5,则这组数据第80百分位数是( )
A.7 B.7.5
C.8 D.9
9.甲从正方形四个顶点中任选两个顶点连成直线,乙也从该正方形四个顶点中任选两个顶点连成直线,则所得的两条直线相互垂直的概率是( )
A.
B.
C.
D.
10.《算数书》竹简于上世纪八十年代在湖北省张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“禾盖”的术:置如其周,令相乘也,又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈L2h相当于将圆锥体积公式中的圆周率π近似取为( )
A.
B.
C.
D.
11.设m,n是两条不同的直线,α,β,γ是三个不同的平面,下列命题中正确的是( )
A.
若m?β,α⊥β,则m⊥α
B.
若m∥α,m⊥β,则α⊥β
C.
若α⊥β,α⊥γ,则β⊥γ
D.
若α∩γ=m,β∩γ=n,m∥n,则α∥β
12.已知多面体ABC-DEFG中(如图),AB、AC、AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则这个多面体的体积为( )
A.
2
B.
4
C.
6
D.
8
二、填空题(共4小题,每小题5分,共20分)
(
第14题
)
(
第13题
)13.如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=________时,CF⊥平面B1DF.
14.已知在直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为__________.
15.在平面直角坐标系xOy中,已知A(1,0),B(0,1),点C在第一象限内,∠AOC=,且OC=2,若=λ+μ,则λ+μ的值是________.
16.在?ABCD中,E和F分别是边CD和BC的中点,=λ+μ,其中λ,μ∈R,则λ+μ=________.
三、解答题(共6小题,共70分)
17.(10分)在△ABC中,内角A,B,C对应的边长分别为a,b,c,已知m=(c,a+b),
n=(a-b,acosB-b),
m∥n.
(1)求角A;
(2)若a=,求b+c的取值范围.
18.(12分)在平面直角坐标系中,已知三点A(4,0),B(t,2),C(6,t),t∈R,O为坐标原点.
(1)若△ABC是直角三角形,求t的值;
(2)若四边形ABCD是平行四边形,求||的最小值.
(
第19题
)19.(12分)在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(1)求证:BD⊥平面AED;
(2)求二面角F-BD-C的余弦值.
20.(12分)在△ABC中,已知·=3·.
(1)求证:tanB=3tanA;
(2)若cosC=,求A的值.
21.(12分)已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)若点D在直线AC上,且⊥,求点D的坐标;
(2)求以BA,BC为邻边的平行四边形的面积.
22.(12分)如图所示,在矩形ABCD中,AB=2,AD=1,E为CD中点,以AE为折痕,把△DAE折起到△D′AE的位置,且平面D′AE⊥平面ABCE.
(1)求证:AD′⊥BE;
(2)求四棱锥D′-ABCE的体积;
(3)在棱ED′上是否存在一点P,使得D′B∥平面PAC,若存在,求出点P的位置,若不存在,请说明理由.
答案解析
1.【答案】B
【解析】由z1=2+i,得1=2-i,
由z2在复平面内对应的点在直线x=1上,
可设z2=1+bi(b∈R),
则1·z2=(2-i)·(1+bi)=2+b+(2b-1)i.
又1·z2为实数,所以2b-1=0,b=.
所以z2=1+i.
2.【答案】B
【解析】因为a=(1,n,2),b=(-2,1,2),
所以2a-b=(4,2n-1,2).
因为2a-b与b垂直,
所以(2a-b)·b=0,
所以-8+2n-1+4=0,
解得n=,所以a=,
所以|a|==.
3.【答案】B
【解析】如图所示,
∵E是OD的中点,∴==b.
又∵△ABE∽△FDE,∴==.
∴=3,∴=.
在△AOE中,=+=a+b,
∴==a+b,故选B.
4.【答案】C
【解析】∵=+=4,∴=3.
∴=-=+-=+-=+(-)-=-,
∴r=,s=-,r-s=,故选C.
5.【答案】D
【解析】设容量为5的样本中本科生的人数为m,由题意可得=,解得m=3,所以样本中有研究生2人,分别记为A,B,本科生3人,分别记为a,b,c,所以从中任意抽取3人的所有情况有(A,B,a),(A,B,b),(A,B,c),(A,a,b),(A,a,c),(A,b,c),(B,a,b),(B,a,c),(B,b,c),(a,b,c),共10种,3人均为本科生的情况只有(a,b,c)1种,所以至少有1人为研究生的概率为=.
6.【答案】C
【解析】因为=(3,4,-8),=(2,-3,1),=(5,1,-7),
·=10-3-7=0,∴BC⊥AC,
而||=,||=5,
所以△ABC是直角三角形.
7.【答案】A
【解析】如图,由斜二测画法原理知,平面中的图形与直观图中的图形上下底边的长度是一样的,不一样的是两个梯形的高,其高的关系是这样的:平面图中的高OA是直观图中O′A′长度的2倍,如直观图,O′A′的长度是直观图中梯形的高的倍,由此平面图中梯形的高OA的长度是直观图中梯形高的2×=2倍,故其面积是梯形O′A′B′C′的面积的2倍,
又∵梯形O′A′B′C′的面积为,
∴原梯形的面积是4.
故选A.
8.【答案】C [该组数据从小到大排列为5,5,6,7,8,9,且6×80%=4.8.所以这组数据的第80百分位数是8.]
9.【答案】C
【解析】甲从正方形四个顶点中任意选择两个顶点连成直线,乙也从正方形四个顶点中任意选择两个顶点连成直线,所得的直线共有6×6=36(对),而相互垂直的有10对,故根据古典概型概率公式得P==.
10.【答案】D
【解析】设圆锥的底面半径为r,则圆锥的底面周长L=2πr,∴r=,∴V=πr2h=.令=L2h,提π=,故选D.
11.【答案】B
【解析】若m?β,α⊥β,则m与α的关系不确定,故A错误;若m∥α,则存在直线n?α,使m∥n,又由m⊥β,可得n⊥β,进而由面面垂直的判定定理得到α⊥β,故B正确;若α⊥β,α⊥γ,则β与γ关系不确定,故C错误;若α∩γ=m,β∩γ=n,m∥n,则α与β可能平行,也可能相交(此时交线与m,n均平行),故D错误.故选B.
12.【答案】B
【解析】取DG中点M,连接CM,AM,FM,则这个多面体的体积可以表示为棱柱BEF-ADM与三棱锥C-FMG以及四棱锥C-ABFM的和.由于多面体ABC-DEFG中(如图),AB、AC、AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,故棱柱BEF-ADM可看作是底面是直角三角形的三棱柱,其高是2,底面是两直角边分别是1,2的三角形,其体积是2××2×1=2.三棱锥C-FMG以CM为高,其长为2,底面是以MF=2,MG=1为直角边的直角三角形,其体积为×2××2×1=.由图形知,C到AM的距离就是四棱锥C-ABFM的高,由于AM=,由等面积法可求得C到AM的距离是,底面四边形是以AM=与AB=2为边长的矩形,故其体积为××2×=.
所以这个多面体的体积为++2=4.
故选B.
13.
【答????案】
a或2a
【解????析】
由已知得B1D⊥AC1,
又CF?平面AC1,∴B1D⊥CF,
故若CF⊥平面B1DF,则必有CF⊥DF.
设AF=x(0<x<3a),则CF2=x2+4a2,
DF2=a2+(3a-x)2,又CD2=a2+9a2=10a2,
∴10a2=x2+4a2+a2+(3a-x)2,
解得x=a或2a.故答案为a或2a.
14.
【答????案】
【解????析】
如图所示,
设=a,=b,=c,则〈a,b〉=120°,c⊥a,c⊥b,
因为=+=-a+c,=+=b+c,
|cos〈,〉|===
===.
15.【答案】+1
【解析】由题意,知=(1,0),=(0,1).
设C(x,y),则=(x,y).
∵=λ+μ,
∴(x,y)=λ(1,0)+μ(0,1)=(λ,μ),
∴又∵∠AOC=,OC=2,
∴λ=x=2cos=,μ=y=2sin=1,
∴λ+μ=+1.
16.
【答????案】
43
【解????析】
设AB→=a,AD→=b,则AC→=a+b,AE→=12a+b,AF→=a+12b,
∴λAE→+μAF→=λ(12a+b)+μ(a+12b)=(12λ+μ)a+(λ+12μ)b,
∴a+b=(12λ+μ)a+(λ+12μ)b,
∴?,,12λ+μ=1,λ+12μ=1,∴,,λ=23,μ=23,∴λ+μ=43.
17.【答案】(1)∵c=a2-b2,由余弦定理
得a2+c2-b2-bc=2a2-2b2,a2=b2+c2-bc.
∵a2=b2+c2-2bccosA,∴cosA=,
∵A∈
(0,π),∴A=.
(2)由正弦定理得===2,
∴b=2sinB,c=2sinC,
∴b+c=2sinB+2sinC=2sinB+2sin
(A+B)
=2sinB+2sinAcosB+2cosAsinB
=2sinB+2×cosB+2×sinB
=3sinB+cosB
=2sin.
∵B∈,∴B+∈,
sin∈,
∴b+c∈.
(1)由题意得AB=(t-4,2),AC=(2,t),BC=(6-t,t-2),
若∠A=90°,则AB?AC=0,即2(t-4)+2t=0,∴t=2;
若∠B=90°,则AB?BC=0,即(t-4)(6-t)+2(t-2)=0,∴t=6±2;
若∠C=90°,则AC?BC=0,即2(6-t)+t(t-2)=0,无解,
∴满足条件的t的值为2或6±2.
(2)若四边形ABCD是平行四边形,则AD=BC,设D的坐标为(x,y),
即(x-4,y)=(6-t,t-2),∴x-4=6-t,y=t-2即D(10-t,t-2),
∴|OD|
2=(10-t)
2+(t-2)
2=2t
2-24t+104,
∴当t=6时,|OD|的最小值为4.
19.【答案】(1)证明 因为四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
所以∠ADC=∠BCD=120°.
又CB=CD,所以∠CDB=30°,
因此∠ADB=90°,即AD⊥BD.
又AE⊥BD,且AE∩AD=A,AE,AD?平面AED,
所以BD⊥平面AED.
(2)解 如图,
取BD的中点G,连接CG,FG,
由于CB=CD,
因此CG⊥BD.
又FC⊥平面ABCD,BD?平面ABCD,
所以FC⊥BD.
由于FC∩CG=C,FC,CG?平面FCG,
所以BD⊥平面FCG,
故BD⊥FG,
所以∠FGC为二面角F-BD-C的平面角.
在等腰三角形BCD中,由于∠BCD=120°,
因此CG=CB.又CB=CF,
所以GF==CG,
故cos∠FGC=,
因此二面角F-BD-C的余弦值为.
20.【答案】(1)证明 因为·=3·,
所以AB·AC·cosA=3BA·BC·cosB,
即AC·cosA=3BC·cosB.
由正弦定理知=,
从而sinBcosA=3sinAcosB.
又因为0
所以tanB=3tanA.
(2)解 因为cosC=,0
从而tanC=2,于是tan[π-(A+B)]=2,
即tan(A+B)=-2,
亦即=-2.
由(1)得=-2,
解得tanA=1或tanA=-.
因为cosA>0,所以tanA=1,所以A=.
21.【答案】解 (1)由题意知,=(1,-3,2),点D在直线AC上,
设=λ=λ(1,-3,2)=(λ,-3λ,2λ),
∴D(λ,2-3λ,2λ+3),
=(λ,2-3λ,3+2λ)-(-2,1,6)
=(λ+2,1-3λ,2λ-3),
∵⊥,
∴·=(1,-3,2)·(λ+2,1-3λ,2λ-3)
=λ+2-3+9λ+4λ-6=14λ-7=0,
∴λ=,
∴D.
(2)∵=(2,1,-3),=(3,-2,-1),
∴||==,
||==,
∴·=2×3+1×(-2)+(-3)×(-1)=7,
∴cosB=cos〈,〉===,
∴sinB=,
∴S=××=7,
∴以BA,BC为邻边的平行四边形的面积为7.
22.【答案】(1)证明 根据题意可知,在长方形ABCD中,△DAE和△CBE为等腰直角三角形,
∴∠DEA=∠CEB=45°,
∴∠AEB=90°,即BE⊥AE.
∵平面D′AE⊥平面ABCE,且平面D′AE∩平面ABCE=AE,BE?平面ABCE,
∴BE⊥平面D′AE,∵AD′?平面D′AE,
∴AD′⊥BE.
(2)解 取AE的中点F,连接D′F,则D′F⊥AE.
∵平面D′AE⊥平面ABCE,
且平面D′AE∩平面ABCE=AE,D′F?平面D′AE,
∴D′F⊥平面ABCE,
∴VD′-ABCE=S四边形ABCE·D′F=××(1+2)×1×=.
(3)解 如图所示,连接AC交BE于Q,假设在D′E上存在点P,使得D′B∥平面PAC,连接PQ.
∵D′B?平面D′BE,
平面D′BE∩平面PAC=PQ,∴D′B∥PQ,
∴在△EBD′中,=.
∵在梯形ABCE中,==,
∴==,即EP=ED′,
∴在棱ED′上存在一点P,且EP=ED′,使得D′B∥平面PAC.
同课章节目录
