华师大版数学七上2.3相反数课件(17张ppt)
文档属性
| 名称 | 华师大版数学七上2.3相反数课件(17张ppt) | 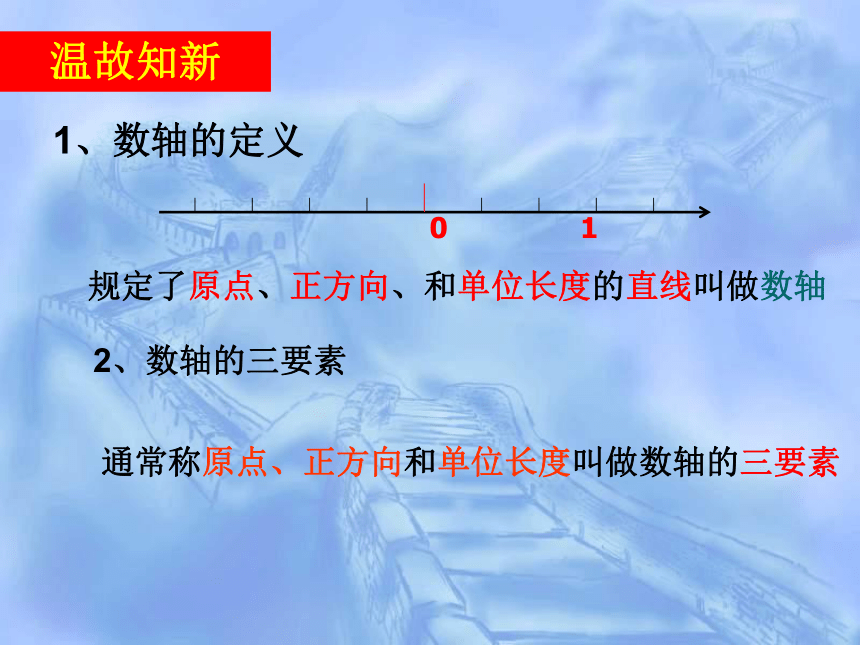 | |
| 格式 | ppt | ||
| 文件大小 | 735.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 13:49:06 | ||
图片预览






文档简介
(共17张PPT)
温故知新
0
1
规定了原点、正方向、和单位长度的直线叫做数轴
通常称原点、正方向和单位长度叫做数轴的三要素
1、数轴的定义
2、数轴的三要素
2.5
2.5
1
1
-
+
+
-
+
-
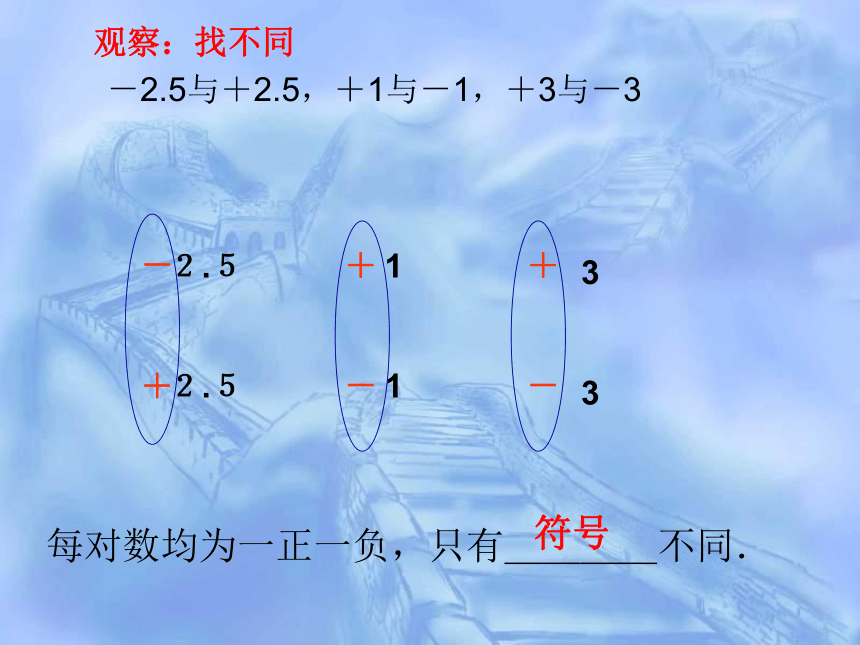
每对数均为一正一负,只有____不同.
符号
3
3
-2.5与+2.5,+1与-1,+3与-3
观察:找不同
§2.3
相反数
只有符号不同的两个数称互为相反数.
规定:
零的相反数是零
.
-2.5与+2.5,+1与-1,+3与-3
0
.
.
+2.5
-2.5
0
.
.
+1
-1
0
.
.
每一对数在数轴上的对应点位于原点的两侧,且到原点的距离相等.
-3
+3
画数轴,并表示出下列各对相反数所在的点.
-
6
和
6,
1.5
和
-
1.5
观察这两对点,每对点各有什么相同和不同.
0
2
-
6
6
-
1.5
1.5
相同点:
不同点:
互为相反数的两个数在数轴上的特点:
与原点的距离相等
位于原点的两旁
我来
辨一辨:
(1)只要符号不同的两个数就称互为相
反数.( )
(2)一个数的相反数一定是负数.( )
(3)零的相反数是零.(
)
(4)-8是相反数.(
)
×
×
√
×
例1:
下列各数的相反数是什么?
解:
的相反数是
的相反数是
的相反数是
的相反数是
的相反数是
一般地,数a
的相反数是-a,a可以是正数,也可以是负数或0。求一个数的相反数即在它前面加一个“-”号。
-a就是表示数a的相反数。
a的相反数是
-a
a
例题尝试
(1)分别写出下列各数的相反数:
+11.2,
-7,
3
,
- ;
(2)指出下列各数是哪个数的相反数:
3.1415926
,
0
,
-
.
例2、说出下列各式的意义并化简符号
(1)-(+3)
(2)-(-4)
解
(1)
-(+3)表示+3的相反数
所以
-(+3)=-3
(2)-(-4)表示-4的相反数
所以-(-4)=4
例题尝试
我来露一手:
化简下列各数:
(1)
-(+10);
(2)
+(-0.15);
(4)
+(-0).
(3)
-7表示__的相反数;
-(-7)
表示___的相反数.
在一个数的前面添上“-”号表示原来这个数的相反数.
在一个数的前面添上“+”号表示这个数本身.
7
-7
-7的相反数是7
求相反数中的有趣发现:
(3)-[-(-2)]
(4)+{-[-(+5)]}
(5)-{-{-…-(-6)}}(共n个负号)
例3、说出下列各式的意义并化简符号
化简的规律是:一个正数前有偶数个负号,结果为正;有奇数个负号,结果为负.
例题尝试
我们一起来议一议:
小丸子说:一个数的相反数一定小于它本
身.你认同她的说法吗?
同学们说:正数的相反数小于它本身;
负数的相反数大于它本身;
零的相反数是零.
看谁掌握得最好:
(1)下列说法正确的是
( )
(A)
与 互为相反数
(B) -( )与+( )互为相反数
(C)5与-(-5)互为相反数
(D)
与-0.125互为相反数
D
(2)下列结论正确的是
(A)
0没有相反数
(B)
符号不同的两个数是相反数
(C)
一个数的相反数的相反数是它本身
(D)
互为相反数的两个数中,一个是正
数,一个是负数
看谁掌握得最好:
(3)一个数的相反数是最小的正整数,则
这个数是____.
看谁掌握得最好:
-1
(3)
数轴上表示相反数的两个对应点,分别位于原点
两侧,它们到原点距离相等;
(1)
只有符号不同的两个数叫做互为相反数;
(2)
相反数成对出现;
(4)
符号的化简方法。
学到了
温故知新
0
1
规定了原点、正方向、和单位长度的直线叫做数轴
通常称原点、正方向和单位长度叫做数轴的三要素
1、数轴的定义
2、数轴的三要素
2.5
2.5
1
1
-
+
+
-
+
-
每对数均为一正一负,只有____不同.
符号
3
3
-2.5与+2.5,+1与-1,+3与-3
观察:找不同
§2.3
相反数
只有符号不同的两个数称互为相反数.
规定:
零的相反数是零
.
-2.5与+2.5,+1与-1,+3与-3
0
.
.
+2.5
-2.5
0
.
.
+1
-1
0
.
.
每一对数在数轴上的对应点位于原点的两侧,且到原点的距离相等.
-3
+3
画数轴,并表示出下列各对相反数所在的点.
-
6
和
6,
1.5
和
-
1.5
观察这两对点,每对点各有什么相同和不同.
0
2
-
6
6
-
1.5
1.5
相同点:
不同点:
互为相反数的两个数在数轴上的特点:
与原点的距离相等
位于原点的两旁
我来
辨一辨:
(1)只要符号不同的两个数就称互为相
反数.( )
(2)一个数的相反数一定是负数.( )
(3)零的相反数是零.(
)
(4)-8是相反数.(
)
×
×
√
×
例1:
下列各数的相反数是什么?
解:
的相反数是
的相反数是
的相反数是
的相反数是
的相反数是
一般地,数a
的相反数是-a,a可以是正数,也可以是负数或0。求一个数的相反数即在它前面加一个“-”号。
-a就是表示数a的相反数。
a的相反数是
-a
a
例题尝试
(1)分别写出下列各数的相反数:
+11.2,
-7,
3
,
- ;
(2)指出下列各数是哪个数的相反数:
3.1415926
,
0
,
-
.
例2、说出下列各式的意义并化简符号
(1)-(+3)
(2)-(-4)
解
(1)
-(+3)表示+3的相反数
所以
-(+3)=-3
(2)-(-4)表示-4的相反数
所以-(-4)=4
例题尝试
我来露一手:
化简下列各数:
(1)
-(+10);
(2)
+(-0.15);
(4)
+(-0).
(3)
-7表示__的相反数;
-(-7)
表示___的相反数.
在一个数的前面添上“-”号表示原来这个数的相反数.
在一个数的前面添上“+”号表示这个数本身.
7
-7
-7的相反数是7
求相反数中的有趣发现:
(3)-[-(-2)]
(4)+{-[-(+5)]}
(5)-{-{-…-(-6)}}(共n个负号)
例3、说出下列各式的意义并化简符号
化简的规律是:一个正数前有偶数个负号,结果为正;有奇数个负号,结果为负.
例题尝试
我们一起来议一议:
小丸子说:一个数的相反数一定小于它本
身.你认同她的说法吗?
同学们说:正数的相反数小于它本身;
负数的相反数大于它本身;
零的相反数是零.
看谁掌握得最好:
(1)下列说法正确的是
( )
(A)
与 互为相反数
(B) -( )与+( )互为相反数
(C)5与-(-5)互为相反数
(D)
与-0.125互为相反数
D
(2)下列结论正确的是
(A)
0没有相反数
(B)
符号不同的两个数是相反数
(C)
一个数的相反数的相反数是它本身
(D)
互为相反数的两个数中,一个是正
数,一个是负数
看谁掌握得最好:
(3)一个数的相反数是最小的正整数,则
这个数是____.
看谁掌握得最好:
-1
(3)
数轴上表示相反数的两个对应点,分别位于原点
两侧,它们到原点距离相等;
(1)
只有符号不同的两个数叫做互为相反数;
(2)
相反数成对出现;
(4)
符号的化简方法。
学到了
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
