八年级人教版数学第十二章12.1《全等三角形》同步测试-2021-2022学年秋季(word版,含解析)
文档属性
| 名称 | 八年级人教版数学第十二章12.1《全等三角形》同步测试-2021-2022学年秋季(word版,含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 334.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-22 21:13:14 | ||
图片预览

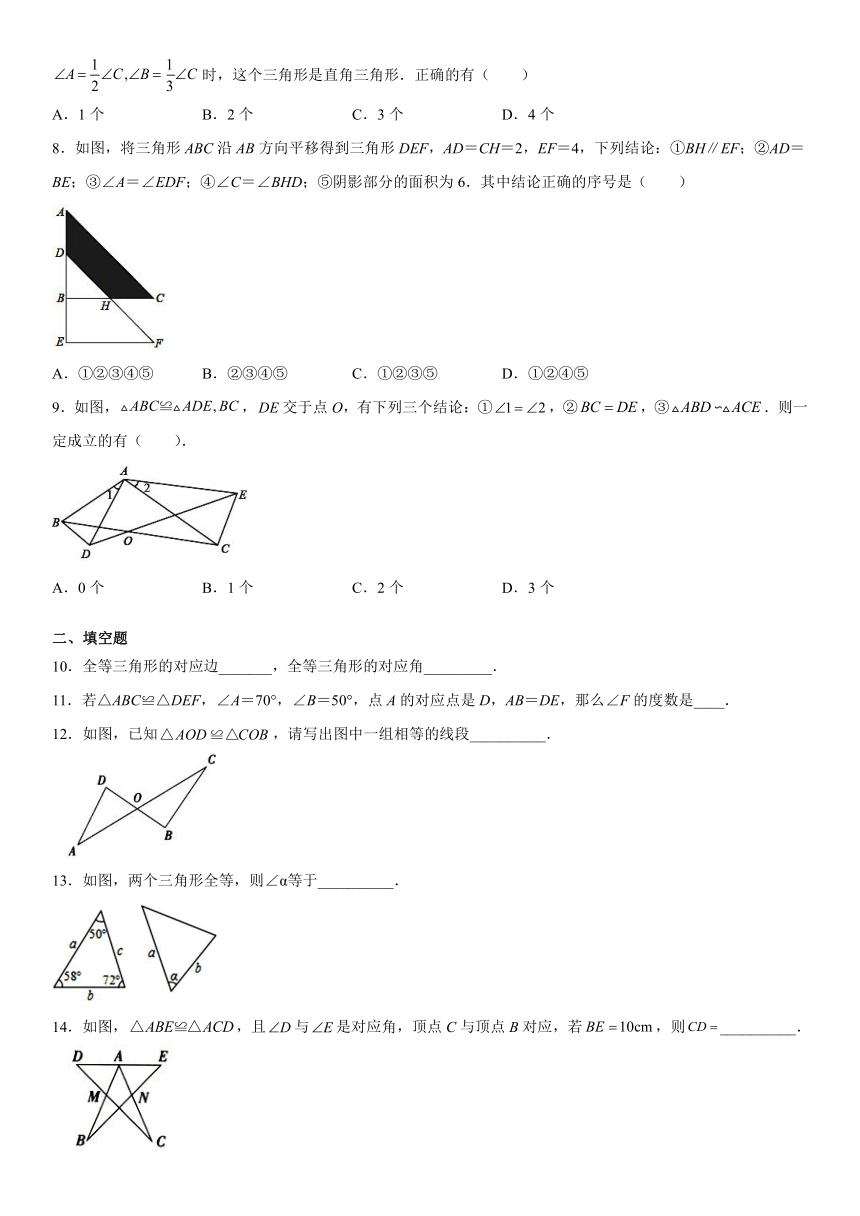
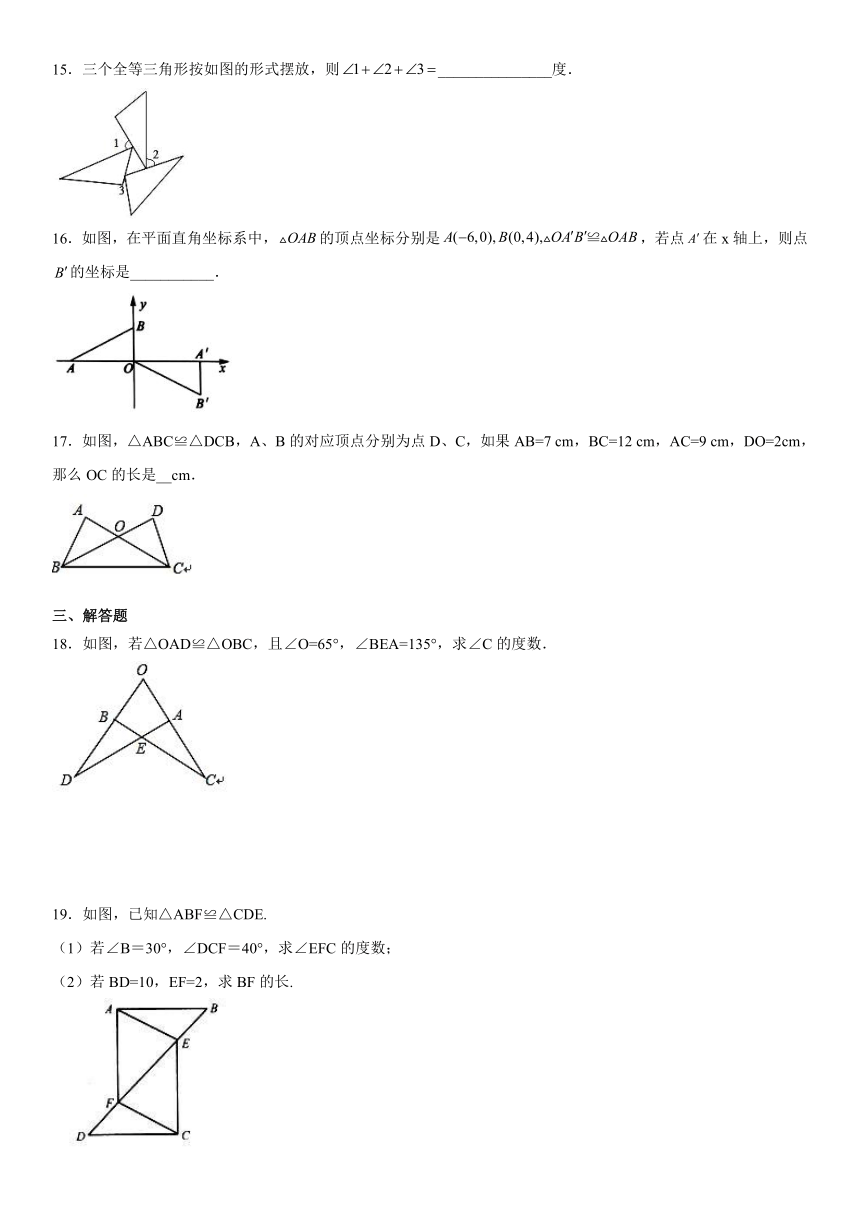


文档简介
八年级人教版数学第十二章12.1《全等三角形》同步测试-2021-2022学年秋季
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列说法中不正确的是(
)
A.能够完全重合的两个图形是全等图形
B.形状相同的两个图形是全等图形
C.大小不同的两个图形不是全等图形
D.形状、大小都相同的两个图形是全等图形
2.下列各组中的两个图形属于全等图形的是(
)
A.
B.
C.
D.
3.如图,ABC≌EFD,则BC与DF的关系是(
)
A.平行但不相等
B.相等但不平行
C.不平行也不相等
D.平行且相等
4.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是( )
A.6cm
B.5cm
C.7cm
D.无法确定
5.如图,△ABE≌△ACD,∠1=∠2,∠B=∠C,下列等式不一定正确的是(
)
A.AB=AC
B.∠BAD=∠CAE
C.BE=CD
D.AD=DE
6.一个三角形的三边长分别为2,5,x,另一个三角形的三边长分别为y,2,6,若这两个三角形全等,则x+y=( )
A.11
B.7
C.8
D.13
7.下列说法:(1)周长相等的两个三角形是全等三角形;(2)周长相等的两个圆是全等图形;(3)如果两个三角形是全等三角形,那么这两个三角形的面积相等;(4)所有的正方形是全等图形;(5)在中,当时,这个三角形是直角三角形.正确的有(
)
A.1个
B.2个
C.3个
D.4个
8.如图,将三角形ABC沿AB方向平移得到三角形DEF,AD=CH=2,EF=4,下列结论:①BH∥EF;②AD=BE;③∠A=∠EDF;④∠C=∠BHD;⑤阴影部分的面积为6.其中结论正确的序号是( )
A.①②③④⑤
B.②③④⑤
C.①②③⑤
D.①②④⑤
9.如图,,交于点O,有下列三个结论:①,②,③.则一定成立的有(
).
A.0个
B.1个
C.2个
D.3个
二、填空题
10.全等三角形的对应边_______,全等三角形的对应角_________.
11.若△ABC≌△DEF,∠A=70°,∠B=50°,点A的对应点是D,AB=DE,那么∠F的度数是____.
12.如图,已知,请写出图中一组相等的线段__________.
13.如图,两个三角形全等,则∠α等于__________.
14.如图,,且与是对应角,顶点C与顶点B对应,若,则__________.
15.三个全等三角形按如图的形式摆放,则_______________度.
16.如图,在平面直角坐标系中,的顶点坐标分别是,若点在x轴上,则点的坐标是___________.
17.如图,△ABC≌△DCB,A、B的对应顶点分别为点D、C,如果AB=7
cm,BC=12
cm,AC=9
cm,DO=2cm,那么OC的长是__cm.
三、解答题
18.如图,若△OAD≌△OBC,且∠O=65°,∠BEA=135°,求∠C的度数.
19.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
20.如图,已知,点E在AB上,DE与AC相交于点F.
(1)当,时,线段AE的长为________;
(2)已知,,
①求的度数;
②求的度数.
参考答案
1.B
【分析】
根据全等图形的定义:能够完全重合的两个图形是全等形,判断即可.
【详解】
解:A、能够完全重合的两个图形是全等形,正确,不合题意;
B、形状相同的两个图形是相似形,故此选项错误,符合题意;
C、大小不同的两个图形不是全等形,正确,不合题意;
D、形状、大小都相同的两个图形是全等形,正确,不合题意;
故选:B.
【点睛】
此题主要考查了全等图形的定义,正确利用全等图形的性质与定义分析是解题关键.
2.B
【分析】
根据全等图形的定义,逐一判断选项,即可.
【详解】
A.两个图形不能完全重合,不是全等图形,不符合题意,
B.两个图形能完全重合,是全等图形,符合题意,
C.两个图形不能完全重合,不是全等图形,不符合题意,
D.两个图形不能完全重合,不是全等图形,不符合题意,
故选B
【点睛】
本题主要考查全等图形的定义,熟练掌握“能完全重合的两个图形,是全等图形”是解题的关键.
3.D
【分析】
根据全等三角形的性质可得BC=FD,∠BCA=∠FDE,再由平行线的判定可推出BC∥FD,即可得出结论.
【详解】
解:∵△ABC≌△EFD,
∴BC=FD,∠BCA=∠FDE,
∴BC∥FD,
即BC与DF的关系是:平行且相等;
故选:D.
【点睛】
本题考查了全等三角形的性质、平行线的判定,掌握全等三角形的性质是解题的关键.
4.C
【分析】
根据全等三角形的性质计算即可;
【详解】
∵△ABC≌△ADE,
∴,
∵BC=7cm,
∴;
故答案选C.
【点睛】
本题主要考查了全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.
5.D
【分析】
由全等三角形的性质可求解.
【详解】
解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,AD=AE,BE=CD,∠BAE=∠CAD,
∴∠BAD=∠CAE
故选D.
【点睛】
本题考查了全等三角形的性质,灵活运用全等三角形的性质是本题的关键.
6.A
【分析】
根据全等三角形的基本性质求解即可.
【详解】
已知这两个三角形全等,则三组对应边应分别为2、5、6,所以x=6,y=5,则
x+y=6+5=11,故本题正确答案为A.
【点睛】
本题主要考查全等三角形的基本性质,掌握全等三角形的基本性质是解决本题的关键.
7.B
【分析】
根据全等的图形判定和性质及直角三角形的判定方法即可判断求解.
【详解】
解:(1)周长相等的两个三角形不一定是全等三角形,故(1)错误;
(2)周长相等的两个圆是全等图形,故(2)正确;
(3)如果两个三角形是全等三角形,那么这两个三角形的面积相等,故(3)正确;
(4)所有的正方形是相似图形,故(4)错误;
(5)在中,当时,
∵∠A+∠B+∠C=180°,
∴∠C+∠C+∠C=180°
∴∠C=°≠90°,
∴这个三角形不是直角三角形,故(5)错误,
故选B.
【点睛】
本题考查全等的图形判定和性质及直角三角形的判定方法,解题的关键是熟练掌握所学知识.
8.A
【分析】
根据平移的性质及全等三角形的性质判断即可.
【详解】
∵将△ABC沿AB方向平移得到△DEF,AD=CH=2,EF=4,
∴BC∥EF,AB=DE,
∴BH∥EF,①正确;
∴AB﹣DB=DE﹣DB,
∴AD=BE,②正确;
③∵将三角形ABC沿AB方向平移得到三角形DEF,
∴△ABC≌△DEF,
∴∠A=∠EDF,③正确;
∵BH∥EF,
∴∠BHD=∠F,
由平移性质可得:∠C=∠F,
∴∠C=∠BHD,④正确;
∵阴影部分的面积=△ABC的面积﹣△DBH的面积=6.⑤正确;
故选:A.
【点睛】
本题考查了全等三角形的判定与性质,直角三角形的面积公式和平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
9.D
【分析】
根据全等三角形的性质可判断①和②,再根据相似三角形的判定判断③即可.
【详解】
解:①∵,
∴∠BAC=∠DAE,
∴∠1+∠DAC=∠2+∠DAC,
∴∠1=∠2,故①成立;
②∵,
∴BC=DE,故②成立,
③∵,
∴AB=AD,AC=AE,
∴,又∠1=∠2,
∴,故③成立,
综上,一定成立的有①②③共3个,
故选:D.
【点睛】
本题考查全等三角形的性质、相似三角形的判定,熟练掌握全等三角形的性质和相似三角形的判定是解答的关键.
10.相等
相等
【详解】
略
11.60°
【分析】
根据全等三角形的对应角相等以及三角形的内角和是180°求解.
【详解】
∵△ABC≌△DEF,∠A=70°,∠B=50°,
∴∠F=∠C=180°﹣∠A﹣∠B=60°.
故答案为:60°.
【点睛】
本题考查了全等三角形的性质.
12.或或(答案不唯一)
【分析】
根据全等三角形的性质可得对应线段相等.
【详解】
解:∵,
∴,,.
故答案为:或或(答案不唯一).
【点睛】
本题考查了全等三角形的性质,对应边相等,能准确找到对应边是解题关键.
13.58°.
【分析】
直接利用全等三角形的性质得出∠α=58°.
【详解】
解:如图所示:∵两个三角形全等,
∴∠α=58°,
故答案为:58°.
【点睛】
本题考察全等三角形的性质,全等三角形的对应角相等.
14.
【分析】
先由“,且与是对应角,点C与点B是对应点”得出CD的对应边为BE,再利用全等三角形的性质,根据BE的长即可求解.
【详解】
∵,且与是对应角,点C与点B是对应点,
∴与是对应边,.
故答案为:.
【点睛】
本题主要考查的是全等三角形的性质,解题关键是观察图形,找出全等三角形的对应点.
15.180°
【分析】
如图所示,利用平角的定义结合三角形内角和性质以及全等三角形性质得出∠4+∠9+∠6=180°,∠5+∠7+∠8=180°,然后进一步求解即可.
【详解】
如图所示,由图形可得:
∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7==540°,
∵三个三角形全等,
∴∠4+∠9+∠6=180°,
∵∠5+∠7+∠8=180°,
∴540°?
180°?
180°=180°,
故答案为:180°.
【点睛】
本题主要考查了全等三角形性质以及三角形内角和性质,熟练掌握相关概念是解题关键.
16.(6,-4)
【分析】
根据全等三角形的性质和点的坐标得出OA=OA′=6,OB=A′B′=4,即可得出答案.
【详解】
解:∵A(-6,0),B(0,4),△OA′B′≌△OAB,
∴OA=OA′=6,OB=A′B′=4,
∴点B′的坐标是(6,-4),
故答案为:(6,-4).
【点睛】
本题考查了坐标与图形性质,全等三角形的性质的应用,解此题的关键是求出OA=OA′=6,OB=A′B′=4.
17.7.
【解析】
试题分析:先根据全等三角形的性质求得AO的长,再结合AC=9cm,即可求得结果.
∵△ABC≌△DCB
∴AO=DO=2cm
∵AC=9cm
∴OC=7cm.
考点:全等三角形的性质
点评:解题的关键是熟练掌握全等三角形的对应边相等,注意对应字母在对应位置上.
18.35?
【分析】
根据全等三角形对应角相等可得∠C=∠D,∠OBC=∠OAD,再根据三角形的内角和等于180°表示出∠OBC,然后利用四边形的内角和等于360°列方程求解即可.
【详解】
∴∠C=∠D,∠OBC=∠OAD,
∵∠O=65?,
∴∠OBC=180??65??∠C=115??∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360?,
∴65?+115??∠C+135?+115??∠C=360?,
解得∠C=35?.
【点睛】
此题考查了全等三角形的性质和四边形的内角和等于360°,熟练掌握这两个性质是解题的关键.
19.(1)70°;(2)6.
【分析】
(1)根据△ABF≌△CDE,可知∠B=∠D,进而利用外角性质求出∠EFC的度数即可;(2)由△ABF≌△CDE可知BF=DE,进而BE=DF,根据BD=10,EF=2即可求出BE=DF=4,进而求出BF的长即可.
【详解】
(1)∵△ABF≌△CDE,
∴∠B=∠D.
∵∠B=30°,
∴∠D=30°.
∵∠DCF=40°,
∴∠EFC=∠D+∠DCF=70°.
(2)∵△ABF≌△CDE,
∴BF=DE
.∵BF=BE+EF,DE=DF+EF,
∴BE=DF.
∵BD=10,EF=2,
∴BE+DF=BD-EF=8,
∴BE=DF=4,
∴BF=BE+EF=6.
【点睛】
本题考查全等三角形的性质,根据三角形全等找出对应边、对应角是解题关键.
20.(1)3;(2)①;②
【分析】
(1)根据全等三角形的性质得出,,即可得出答案;
(2)①根据三角形全等的性质得出,,根据三角形内角和定理求出,即可得到结论;
②根据三角形外角性质求出,根据三角形外角性质求出即可;
【详解】
(1),,,
,,
.
(2)①,
,.
,
,
.
②是的外角,
.
是的外角,
.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列说法中不正确的是(
)
A.能够完全重合的两个图形是全等图形
B.形状相同的两个图形是全等图形
C.大小不同的两个图形不是全等图形
D.形状、大小都相同的两个图形是全等图形
2.下列各组中的两个图形属于全等图形的是(
)
A.
B.
C.
D.
3.如图,ABC≌EFD,则BC与DF的关系是(
)
A.平行但不相等
B.相等但不平行
C.不平行也不相等
D.平行且相等
4.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是( )
A.6cm
B.5cm
C.7cm
D.无法确定
5.如图,△ABE≌△ACD,∠1=∠2,∠B=∠C,下列等式不一定正确的是(
)
A.AB=AC
B.∠BAD=∠CAE
C.BE=CD
D.AD=DE
6.一个三角形的三边长分别为2,5,x,另一个三角形的三边长分别为y,2,6,若这两个三角形全等,则x+y=( )
A.11
B.7
C.8
D.13
7.下列说法:(1)周长相等的两个三角形是全等三角形;(2)周长相等的两个圆是全等图形;(3)如果两个三角形是全等三角形,那么这两个三角形的面积相等;(4)所有的正方形是全等图形;(5)在中,当时,这个三角形是直角三角形.正确的有(
)
A.1个
B.2个
C.3个
D.4个
8.如图,将三角形ABC沿AB方向平移得到三角形DEF,AD=CH=2,EF=4,下列结论:①BH∥EF;②AD=BE;③∠A=∠EDF;④∠C=∠BHD;⑤阴影部分的面积为6.其中结论正确的序号是( )
A.①②③④⑤
B.②③④⑤
C.①②③⑤
D.①②④⑤
9.如图,,交于点O,有下列三个结论:①,②,③.则一定成立的有(
).
A.0个
B.1个
C.2个
D.3个
二、填空题
10.全等三角形的对应边_______,全等三角形的对应角_________.
11.若△ABC≌△DEF,∠A=70°,∠B=50°,点A的对应点是D,AB=DE,那么∠F的度数是____.
12.如图,已知,请写出图中一组相等的线段__________.
13.如图,两个三角形全等,则∠α等于__________.
14.如图,,且与是对应角,顶点C与顶点B对应,若,则__________.
15.三个全等三角形按如图的形式摆放,则_______________度.
16.如图,在平面直角坐标系中,的顶点坐标分别是,若点在x轴上,则点的坐标是___________.
17.如图,△ABC≌△DCB,A、B的对应顶点分别为点D、C,如果AB=7
cm,BC=12
cm,AC=9
cm,DO=2cm,那么OC的长是__cm.
三、解答题
18.如图,若△OAD≌△OBC,且∠O=65°,∠BEA=135°,求∠C的度数.
19.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
20.如图,已知,点E在AB上,DE与AC相交于点F.
(1)当,时,线段AE的长为________;
(2)已知,,
①求的度数;
②求的度数.
参考答案
1.B
【分析】
根据全等图形的定义:能够完全重合的两个图形是全等形,判断即可.
【详解】
解:A、能够完全重合的两个图形是全等形,正确,不合题意;
B、形状相同的两个图形是相似形,故此选项错误,符合题意;
C、大小不同的两个图形不是全等形,正确,不合题意;
D、形状、大小都相同的两个图形是全等形,正确,不合题意;
故选:B.
【点睛】
此题主要考查了全等图形的定义,正确利用全等图形的性质与定义分析是解题关键.
2.B
【分析】
根据全等图形的定义,逐一判断选项,即可.
【详解】
A.两个图形不能完全重合,不是全等图形,不符合题意,
B.两个图形能完全重合,是全等图形,符合题意,
C.两个图形不能完全重合,不是全等图形,不符合题意,
D.两个图形不能完全重合,不是全等图形,不符合题意,
故选B
【点睛】
本题主要考查全等图形的定义,熟练掌握“能完全重合的两个图形,是全等图形”是解题的关键.
3.D
【分析】
根据全等三角形的性质可得BC=FD,∠BCA=∠FDE,再由平行线的判定可推出BC∥FD,即可得出结论.
【详解】
解:∵△ABC≌△EFD,
∴BC=FD,∠BCA=∠FDE,
∴BC∥FD,
即BC与DF的关系是:平行且相等;
故选:D.
【点睛】
本题考查了全等三角形的性质、平行线的判定,掌握全等三角形的性质是解题的关键.
4.C
【分析】
根据全等三角形的性质计算即可;
【详解】
∵△ABC≌△ADE,
∴,
∵BC=7cm,
∴;
故答案选C.
【点睛】
本题主要考查了全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.
5.D
【分析】
由全等三角形的性质可求解.
【详解】
解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,AD=AE,BE=CD,∠BAE=∠CAD,
∴∠BAD=∠CAE
故选D.
【点睛】
本题考查了全等三角形的性质,灵活运用全等三角形的性质是本题的关键.
6.A
【分析】
根据全等三角形的基本性质求解即可.
【详解】
已知这两个三角形全等,则三组对应边应分别为2、5、6,所以x=6,y=5,则
x+y=6+5=11,故本题正确答案为A.
【点睛】
本题主要考查全等三角形的基本性质,掌握全等三角形的基本性质是解决本题的关键.
7.B
【分析】
根据全等的图形判定和性质及直角三角形的判定方法即可判断求解.
【详解】
解:(1)周长相等的两个三角形不一定是全等三角形,故(1)错误;
(2)周长相等的两个圆是全等图形,故(2)正确;
(3)如果两个三角形是全等三角形,那么这两个三角形的面积相等,故(3)正确;
(4)所有的正方形是相似图形,故(4)错误;
(5)在中,当时,
∵∠A+∠B+∠C=180°,
∴∠C+∠C+∠C=180°
∴∠C=°≠90°,
∴这个三角形不是直角三角形,故(5)错误,
故选B.
【点睛】
本题考查全等的图形判定和性质及直角三角形的判定方法,解题的关键是熟练掌握所学知识.
8.A
【分析】
根据平移的性质及全等三角形的性质判断即可.
【详解】
∵将△ABC沿AB方向平移得到△DEF,AD=CH=2,EF=4,
∴BC∥EF,AB=DE,
∴BH∥EF,①正确;
∴AB﹣DB=DE﹣DB,
∴AD=BE,②正确;
③∵将三角形ABC沿AB方向平移得到三角形DEF,
∴△ABC≌△DEF,
∴∠A=∠EDF,③正确;
∵BH∥EF,
∴∠BHD=∠F,
由平移性质可得:∠C=∠F,
∴∠C=∠BHD,④正确;
∵阴影部分的面积=△ABC的面积﹣△DBH的面积=6.⑤正确;
故选:A.
【点睛】
本题考查了全等三角形的判定与性质,直角三角形的面积公式和平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
9.D
【分析】
根据全等三角形的性质可判断①和②,再根据相似三角形的判定判断③即可.
【详解】
解:①∵,
∴∠BAC=∠DAE,
∴∠1+∠DAC=∠2+∠DAC,
∴∠1=∠2,故①成立;
②∵,
∴BC=DE,故②成立,
③∵,
∴AB=AD,AC=AE,
∴,又∠1=∠2,
∴,故③成立,
综上,一定成立的有①②③共3个,
故选:D.
【点睛】
本题考查全等三角形的性质、相似三角形的判定,熟练掌握全等三角形的性质和相似三角形的判定是解答的关键.
10.相等
相等
【详解】
略
11.60°
【分析】
根据全等三角形的对应角相等以及三角形的内角和是180°求解.
【详解】
∵△ABC≌△DEF,∠A=70°,∠B=50°,
∴∠F=∠C=180°﹣∠A﹣∠B=60°.
故答案为:60°.
【点睛】
本题考查了全等三角形的性质.
12.或或(答案不唯一)
【分析】
根据全等三角形的性质可得对应线段相等.
【详解】
解:∵,
∴,,.
故答案为:或或(答案不唯一).
【点睛】
本题考查了全等三角形的性质,对应边相等,能准确找到对应边是解题关键.
13.58°.
【分析】
直接利用全等三角形的性质得出∠α=58°.
【详解】
解:如图所示:∵两个三角形全等,
∴∠α=58°,
故答案为:58°.
【点睛】
本题考察全等三角形的性质,全等三角形的对应角相等.
14.
【分析】
先由“,且与是对应角,点C与点B是对应点”得出CD的对应边为BE,再利用全等三角形的性质,根据BE的长即可求解.
【详解】
∵,且与是对应角,点C与点B是对应点,
∴与是对应边,.
故答案为:.
【点睛】
本题主要考查的是全等三角形的性质,解题关键是观察图形,找出全等三角形的对应点.
15.180°
【分析】
如图所示,利用平角的定义结合三角形内角和性质以及全等三角形性质得出∠4+∠9+∠6=180°,∠5+∠7+∠8=180°,然后进一步求解即可.
【详解】
如图所示,由图形可得:
∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7==540°,
∵三个三角形全等,
∴∠4+∠9+∠6=180°,
∵∠5+∠7+∠8=180°,
∴540°?
180°?
180°=180°,
故答案为:180°.
【点睛】
本题主要考查了全等三角形性质以及三角形内角和性质,熟练掌握相关概念是解题关键.
16.(6,-4)
【分析】
根据全等三角形的性质和点的坐标得出OA=OA′=6,OB=A′B′=4,即可得出答案.
【详解】
解:∵A(-6,0),B(0,4),△OA′B′≌△OAB,
∴OA=OA′=6,OB=A′B′=4,
∴点B′的坐标是(6,-4),
故答案为:(6,-4).
【点睛】
本题考查了坐标与图形性质,全等三角形的性质的应用,解此题的关键是求出OA=OA′=6,OB=A′B′=4.
17.7.
【解析】
试题分析:先根据全等三角形的性质求得AO的长,再结合AC=9cm,即可求得结果.
∵△ABC≌△DCB
∴AO=DO=2cm
∵AC=9cm
∴OC=7cm.
考点:全等三角形的性质
点评:解题的关键是熟练掌握全等三角形的对应边相等,注意对应字母在对应位置上.
18.35?
【分析】
根据全等三角形对应角相等可得∠C=∠D,∠OBC=∠OAD,再根据三角形的内角和等于180°表示出∠OBC,然后利用四边形的内角和等于360°列方程求解即可.
【详解】
∴∠C=∠D,∠OBC=∠OAD,
∵∠O=65?,
∴∠OBC=180??65??∠C=115??∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360?,
∴65?+115??∠C+135?+115??∠C=360?,
解得∠C=35?.
【点睛】
此题考查了全等三角形的性质和四边形的内角和等于360°,熟练掌握这两个性质是解题的关键.
19.(1)70°;(2)6.
【分析】
(1)根据△ABF≌△CDE,可知∠B=∠D,进而利用外角性质求出∠EFC的度数即可;(2)由△ABF≌△CDE可知BF=DE,进而BE=DF,根据BD=10,EF=2即可求出BE=DF=4,进而求出BF的长即可.
【详解】
(1)∵△ABF≌△CDE,
∴∠B=∠D.
∵∠B=30°,
∴∠D=30°.
∵∠DCF=40°,
∴∠EFC=∠D+∠DCF=70°.
(2)∵△ABF≌△CDE,
∴BF=DE
.∵BF=BE+EF,DE=DF+EF,
∴BE=DF.
∵BD=10,EF=2,
∴BE+DF=BD-EF=8,
∴BE=DF=4,
∴BF=BE+EF=6.
【点睛】
本题考查全等三角形的性质,根据三角形全等找出对应边、对应角是解题关键.
20.(1)3;(2)①;②
【分析】
(1)根据全等三角形的性质得出,,即可得出答案;
(2)①根据三角形全等的性质得出,,根据三角形内角和定理求出,即可得到结论;
②根据三角形外角性质求出,根据三角形外角性质求出即可;
【详解】
(1),,,
,,
.
(2)①,
,.
,
,
.
②是的外角,
.
是的外角,
.
