北师大版数学五年级上册 数学好玩 第3课时 尝试与猜测 教案
文档属性
| 名称 | 北师大版数学五年级上册 数学好玩 第3课时 尝试与猜测 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 252.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 00:00:00 | ||
图片预览



文档简介
尝试与猜测
【学习内容】
p99—p100页
【学习目标】
1、学会用列表例举法解答“鸡兔同笼问题”,比较各种列举法的特点,并让学生体会怎样列举更简便。
?2、通过合作交流探索多种列表方法解决鸡兔同笼问题并学会用这种方法解决生活中类似的实际问题。
3、初步认识“鸡兔同笼”的数学趣题,了解与此有关的数学史,学习我国传统的数学文化。
?【学习重点】借助“鸡兔同笼”这个载体让学生经历列表、尝试和不断调整的过程,从中体会出解决问题的一般策略——假设列表法。
【学习难点】解决此类问题的调整策略既:在运用“跳跃列举”中的调整幅度的大小,和在使用“折中列举”后巧妙的运用“跳跃列举”。
一、看一看,自主学习列表法。
1、课件直接出示课题,师:同学们今天这节课我们要一起学习新课《尝试与猜测》。
2、课件出示学习目标,师:这节课的学习目标是全班齐读:①结合解决“鸡兔同笼”的问题,体验用列表例举法进行尝试与猜测的解题策略;
②了解尝试与猜测、列表策略还适用于哪些问题。
3、师:“鸡兔同笼”问题是我国古代数学名题之一,出自大约一千五百年前数学名著《孙子算经》下卷第31题
。(课件显示)
二、说一说,合作学习列表法。
全班交流:
1、淘气和笑笑用什么方法来进行尝试与猜测的?(列表法)
2、表格中的1和8、2和7、3和6、4和5是怎样尝试的?依据是什么?
3、表格中34是怎样得到的?
1×2+8×4=34(条)
板书:
—
=
2(条)
4、表格右侧一排(X
X
X
X
√)是什么意思?
5、从上往下看,你有什么发现?(课件显示:鸡兔的总只数是固定的,
每增加1只鸡,兔减少1只,腿就会减少2条。)
6、师:每增加2只鸡,兔减少2只,腿就会减少(4
)条。
每增加5只鸡,兔减少5只,腿就会减少(10)条。
7、书上的列表法是怎样假设的?是不是一定要一只一只的举例呢?
(设计意图:“鸡兔同笼”的问题,本课主要是让学生体验列表进行尝试与猜测的解题策略,让学生自主学习课本中淘气与笑笑的方法,重点是让学生知道怎样列表,用列表法来解决这类问题有什么规律等,为后面探究还可以怎样列表?怎样更快捷的列表起了很好的铺垫。)
三、做一做,动手体验列表法。
师:接下来就让我们一起来解决这个千年古题:(课件出示)今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
师:让我们像古人一样再读一读。
师:你读懂了什么?随着学生的回答课件出示:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
请同学们自主独立用列表法来解决下吧!(个别学生板演)
鸡有几只
兔有几只
腿有多少条
四、改一改,展示不同列表法。
请有不同列法的同学上台更正。
(设计意图:在全班交流中学生理解用列表法解决鸡兔问题,让学生自己试用解决千年古题,由于数字大,在学生进行逐一列表之后,部分学生必定会想到用跳跃列表法)
五、议一议,加深理解列表法。
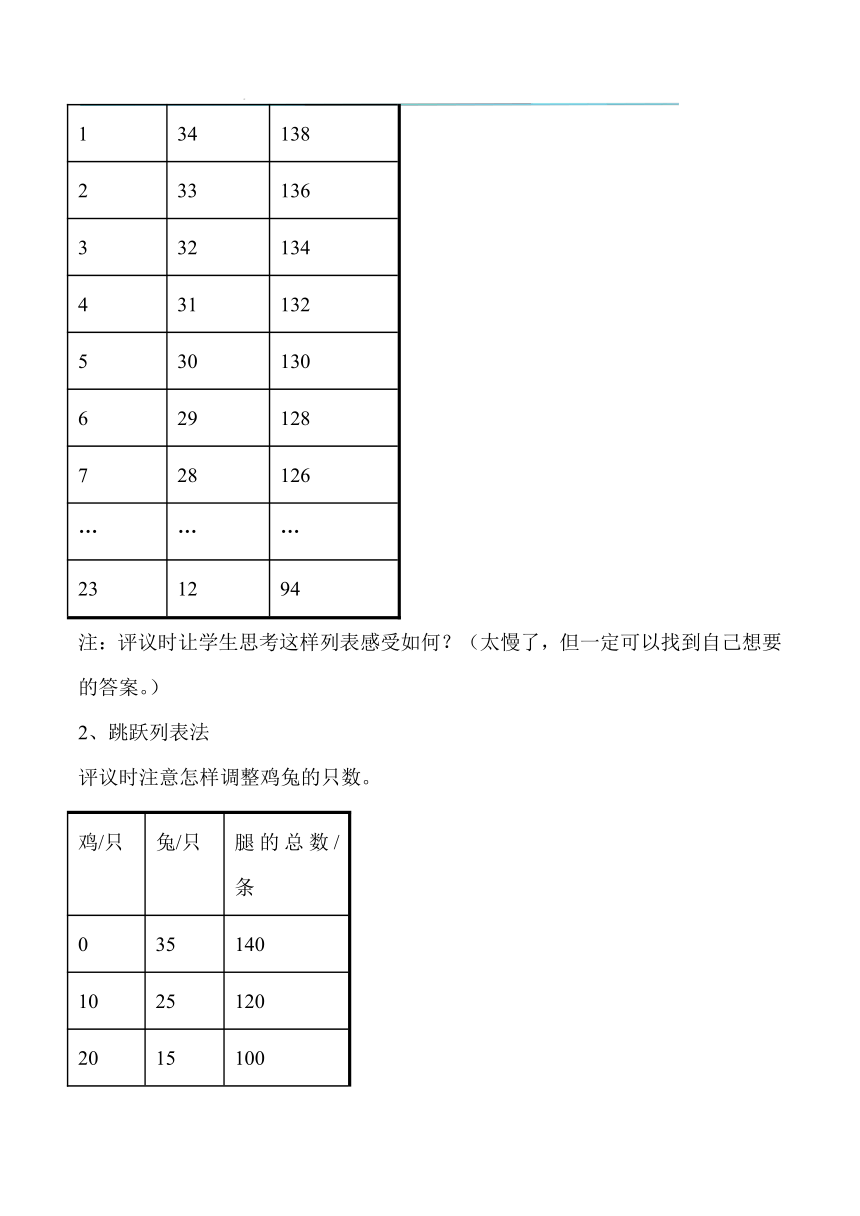
1、
逐一列表法
鸡/只
兔/只
腿的总数/条
1
34
138
2
33
136
3
32
134
4
31
132
5
30
130
6
29
128
7
28
126
…
…
…
23
12
94
注:评议时让学生思考这样列表感受如何?(太慢了,但一定可以找到自己想要的答案。)
2、跳跃列表法
评议时注意怎样调整鸡兔的只数。
鸡/只
兔/只
腿的总数/条
0
35
140
10
25
120
20
15
100
25
10
90
22
13
92
23
12
94
3、折中列表法
鸡/只
兔/只
腿的总数/条
17
18
106
20
15
100
22
13
96
23
12
94
师:三种列表法比较下,各有什么优点?哪种列表法更好?
4、师:老师这还有一种更快的列表法想看吗?
鸡/只
兔/只
腿的总数/条
17
18
106
23
12
94
师:你知道老师是怎样调整的?
生:12÷2=6(只)
鸡:
17+6=13(只)
兔:18-6=12(只)
师:为什么除以6呢?
生:因为每增加1只鸡,兔减少1只,腿就会减少2条。要调整12条腿,12里有几个2,就要调整几只。
小结:我们用列表法进行尝试时,还应该边例举边思考,这样才能更快的解决问题。
六、练一练,强化提升列表法。
1、师:你觉得“鸡兔同笼”问题是什么样的问题?
师:同学们,“鸡兔同笼”抓住数学的本质,这里的鸡不仅仅代表鸡,这里的兔也不仅仅代表兔。“鸡兔同笼”问题漂洋过海,传到日本等国,就变成了“龟鹤问题”,你认为“龟鹤问题”与“鸡兔同笼”有什么相似之处?
龟鹤同笼,有20头,54条腿,龟鹤各多少只?
鹤相当于
鸡
龟相当于
兔
2、停车场里的“鸡兔同笼”问题
停车场停着20辆车,有轿车和三轮车,已知有70个车轮,求三轮车有多少辆?汽车有多少辆?
三轮车相当于
鸡
轿车相当于
兔
3、存钱罐里的“鸡兔同笼”问题
乐乐的存钱罐里有1角和5角的硬币共27枚,价值5.1元,1角和5角的硬币各有多少枚?
1角相当于
鸡
5角相当于
兔
4、师:那就请同学解决一下存钱罐里的“鸡兔同笼”问题
吧!
乐乐的存钱罐里有1角和5角的硬币共27枚,价值5.1元,1角和5角的硬币各有多少枚?
1)学生独立完成。
2)汇报:你采用的是那种方法?为什么要选用这种列表方法?就这道题而言你认为用那种方法解决最好?
1角/枚
5角/枚
总价值/元
14
13
7.9
21
7
5.1
……
……
……
计算方式:
7.9-5.1=2.8(元
)
2.8
÷0.4=7(枚)
14+7=21(枚)
13-6=7(枚)
6、师小结:鸡兔同笼的各种解法除了列表法,鸡兔同笼的解法还有假设法、方程法、画图法、抬足法……
欣赏孙子巧解“鸡兔同笼”:砍足法。和画图法。
7、愿意告诉老师这节课你的学习收获吗?
8、结束语:最后黎老师送给大家两句话:认真观察就会有所发现,立于善于思考就会有所收获。我相信同学们只要敢于猜测与尝试、并且不断的实践验证、调整创新,任何问题都能迎刃而解。
这么多的腿?一定是兔子太多了
腿还多,兔子数还应减少。
比94少了,兔子
数应该在15和10
之间。
差不多了,
再调一点。
先假设鸡和兔的只数差不多。
106条比94条多了12条,可以……
【学习内容】
p99—p100页
【学习目标】
1、学会用列表例举法解答“鸡兔同笼问题”,比较各种列举法的特点,并让学生体会怎样列举更简便。
?2、通过合作交流探索多种列表方法解决鸡兔同笼问题并学会用这种方法解决生活中类似的实际问题。
3、初步认识“鸡兔同笼”的数学趣题,了解与此有关的数学史,学习我国传统的数学文化。
?【学习重点】借助“鸡兔同笼”这个载体让学生经历列表、尝试和不断调整的过程,从中体会出解决问题的一般策略——假设列表法。
【学习难点】解决此类问题的调整策略既:在运用“跳跃列举”中的调整幅度的大小,和在使用“折中列举”后巧妙的运用“跳跃列举”。
一、看一看,自主学习列表法。
1、课件直接出示课题,师:同学们今天这节课我们要一起学习新课《尝试与猜测》。
2、课件出示学习目标,师:这节课的学习目标是全班齐读:①结合解决“鸡兔同笼”的问题,体验用列表例举法进行尝试与猜测的解题策略;
②了解尝试与猜测、列表策略还适用于哪些问题。
3、师:“鸡兔同笼”问题是我国古代数学名题之一,出自大约一千五百年前数学名著《孙子算经》下卷第31题
。(课件显示)
二、说一说,合作学习列表法。
全班交流:
1、淘气和笑笑用什么方法来进行尝试与猜测的?(列表法)
2、表格中的1和8、2和7、3和6、4和5是怎样尝试的?依据是什么?
3、表格中34是怎样得到的?
1×2+8×4=34(条)
板书:
—
=
2(条)
4、表格右侧一排(X
X
X
X
√)是什么意思?
5、从上往下看,你有什么发现?(课件显示:鸡兔的总只数是固定的,
每增加1只鸡,兔减少1只,腿就会减少2条。)
6、师:每增加2只鸡,兔减少2只,腿就会减少(4
)条。
每增加5只鸡,兔减少5只,腿就会减少(10)条。
7、书上的列表法是怎样假设的?是不是一定要一只一只的举例呢?
(设计意图:“鸡兔同笼”的问题,本课主要是让学生体验列表进行尝试与猜测的解题策略,让学生自主学习课本中淘气与笑笑的方法,重点是让学生知道怎样列表,用列表法来解决这类问题有什么规律等,为后面探究还可以怎样列表?怎样更快捷的列表起了很好的铺垫。)
三、做一做,动手体验列表法。
师:接下来就让我们一起来解决这个千年古题:(课件出示)今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
师:让我们像古人一样再读一读。
师:你读懂了什么?随着学生的回答课件出示:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
请同学们自主独立用列表法来解决下吧!(个别学生板演)
鸡有几只
兔有几只
腿有多少条
四、改一改,展示不同列表法。
请有不同列法的同学上台更正。
(设计意图:在全班交流中学生理解用列表法解决鸡兔问题,让学生自己试用解决千年古题,由于数字大,在学生进行逐一列表之后,部分学生必定会想到用跳跃列表法)
五、议一议,加深理解列表法。
1、
逐一列表法
鸡/只
兔/只
腿的总数/条
1
34
138
2
33
136
3
32
134
4
31
132
5
30
130
6
29
128
7
28
126
…
…
…
23
12
94
注:评议时让学生思考这样列表感受如何?(太慢了,但一定可以找到自己想要的答案。)
2、跳跃列表法
评议时注意怎样调整鸡兔的只数。
鸡/只
兔/只
腿的总数/条
0
35
140
10
25
120
20
15
100
25
10
90
22
13
92
23
12
94
3、折中列表法
鸡/只
兔/只
腿的总数/条
17
18
106
20
15
100
22
13
96
23
12
94
师:三种列表法比较下,各有什么优点?哪种列表法更好?
4、师:老师这还有一种更快的列表法想看吗?
鸡/只
兔/只
腿的总数/条
17
18
106
23
12
94
师:你知道老师是怎样调整的?
生:12÷2=6(只)
鸡:
17+6=13(只)
兔:18-6=12(只)
师:为什么除以6呢?
生:因为每增加1只鸡,兔减少1只,腿就会减少2条。要调整12条腿,12里有几个2,就要调整几只。
小结:我们用列表法进行尝试时,还应该边例举边思考,这样才能更快的解决问题。
六、练一练,强化提升列表法。
1、师:你觉得“鸡兔同笼”问题是什么样的问题?
师:同学们,“鸡兔同笼”抓住数学的本质,这里的鸡不仅仅代表鸡,这里的兔也不仅仅代表兔。“鸡兔同笼”问题漂洋过海,传到日本等国,就变成了“龟鹤问题”,你认为“龟鹤问题”与“鸡兔同笼”有什么相似之处?
龟鹤同笼,有20头,54条腿,龟鹤各多少只?
鹤相当于
鸡
龟相当于
兔
2、停车场里的“鸡兔同笼”问题
停车场停着20辆车,有轿车和三轮车,已知有70个车轮,求三轮车有多少辆?汽车有多少辆?
三轮车相当于
鸡
轿车相当于
兔
3、存钱罐里的“鸡兔同笼”问题
乐乐的存钱罐里有1角和5角的硬币共27枚,价值5.1元,1角和5角的硬币各有多少枚?
1角相当于
鸡
5角相当于
兔
4、师:那就请同学解决一下存钱罐里的“鸡兔同笼”问题
吧!
乐乐的存钱罐里有1角和5角的硬币共27枚,价值5.1元,1角和5角的硬币各有多少枚?
1)学生独立完成。
2)汇报:你采用的是那种方法?为什么要选用这种列表方法?就这道题而言你认为用那种方法解决最好?
1角/枚
5角/枚
总价值/元
14
13
7.9
21
7
5.1
……
……
……
计算方式:
7.9-5.1=2.8(元
)
2.8
÷0.4=7(枚)
14+7=21(枚)
13-6=7(枚)
6、师小结:鸡兔同笼的各种解法除了列表法,鸡兔同笼的解法还有假设法、方程法、画图法、抬足法……
欣赏孙子巧解“鸡兔同笼”:砍足法。和画图法。
7、愿意告诉老师这节课你的学习收获吗?
8、结束语:最后黎老师送给大家两句话:认真观察就会有所发现,立于善于思考就会有所收获。我相信同学们只要敢于猜测与尝试、并且不断的实践验证、调整创新,任何问题都能迎刃而解。
这么多的腿?一定是兔子太多了
腿还多,兔子数还应减少。
比94少了,兔子
数应该在15和10
之间。
差不多了,
再调一点。
先假设鸡和兔的只数差不多。
106条比94条多了12条,可以……
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
