2021-2022学年华东师大版数学九年级上册23.1.2平行线分线段成比例 课后练习(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级上册23.1.2平行线分线段成比例 课后练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 635.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 14:03:38 | ||
图片预览
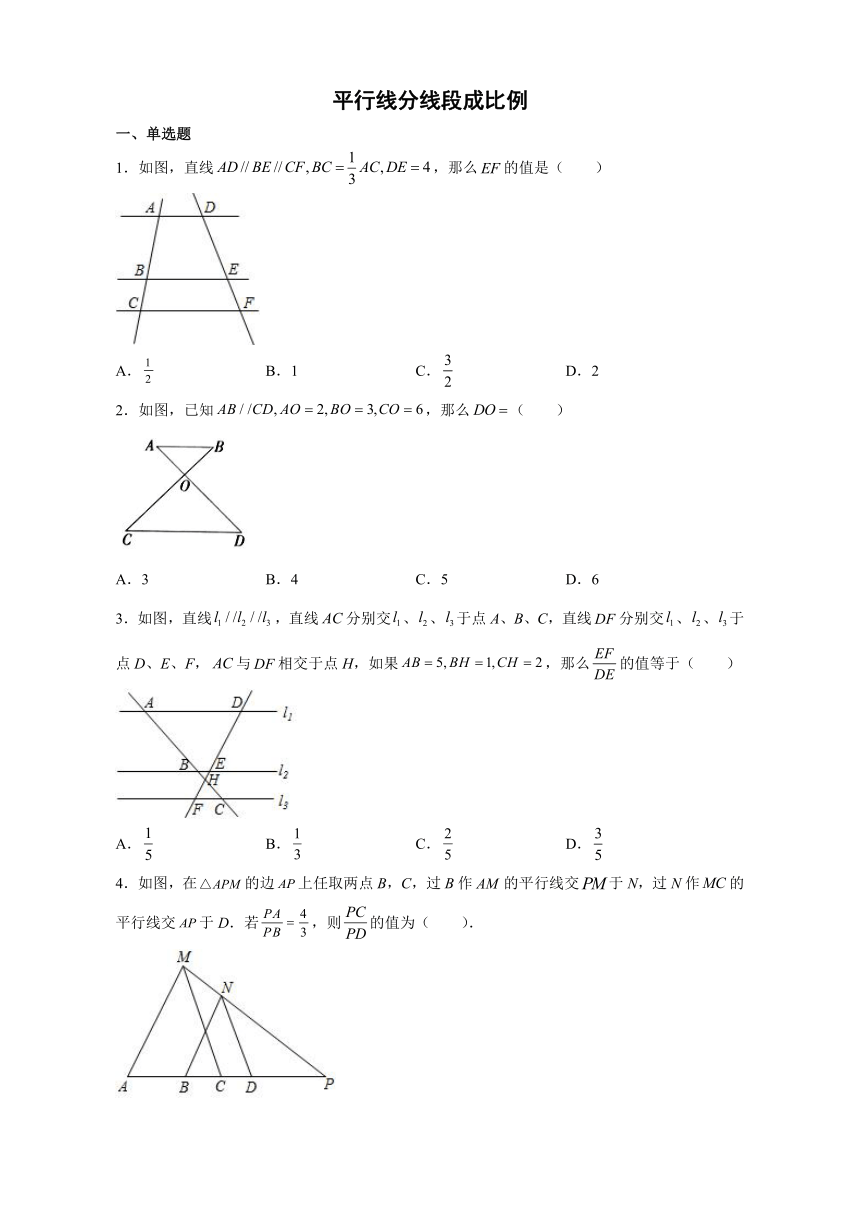


文档简介
平行线分线段成比例
一、单选题
1.如图,直线,那么的值是(
)
A.
B.1
C.
D.2
2.如图,已知,那么(
)
A.3
B.4
C.5
D.6
3.如图,直线,直线分别交、、于点A、B、C,直线分别交、、于点D、E、F,与相交于点H,如果,那么的值等于(
)
A.
B.
C.
D.
4.如图,在的边上任取两点B,C,过B作的平行线交于N,过N作的平行线交于D.若,则的值为(
).
A.
B.
C.2
D.3
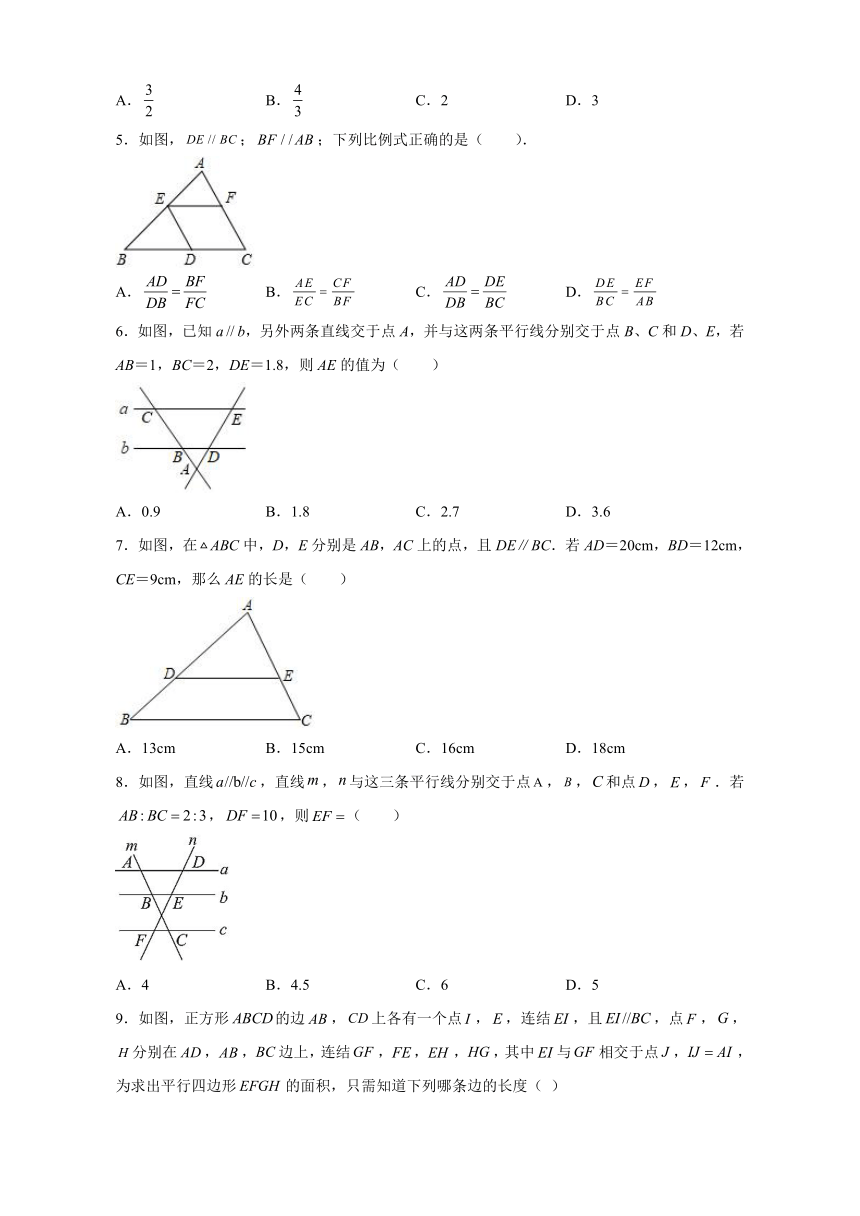
5.如图,;;下列比例式正确的是(
).
A.
B.
C.
D.
6.如图,已知ab,另外两条直线交于点A,并与这两条平行线分别交于点B、C和D、E,若AB=1,BC=2,DE=1.8,则AE的值为( )
A.0.9
B.1.8
C.2.7
D.3.6
7.如图,在ABC中,D,E分别是AB,AC上的点,且DE∥BC.若AD=20cm,BD=12cm,CE=9cm,那么AE的长是(
)
A.13cm
B.15cm
C.16cm
D.18cm
8.如图,直线,直线,与这三条平行线分别交于点,,和点,,.若,,则(
)
A.4
B.4.5
C.6
D.5
9.如图,正方形的边,上各有一个点,,连结,且,点,,分别在,,边上,连结,,,,其中与相交于点,,为求出平行四边形的面积,只需知道下列哪条边的长度(
)
A.
B.
C.
D.
10.如图:在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GEBD,且交AB于点E,GFAC,且交CD于点F,则下列结论一定正确的是(
)
A.
B.
C.
D.
11.如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论错误的是(
)
A.
B.
C.
D.
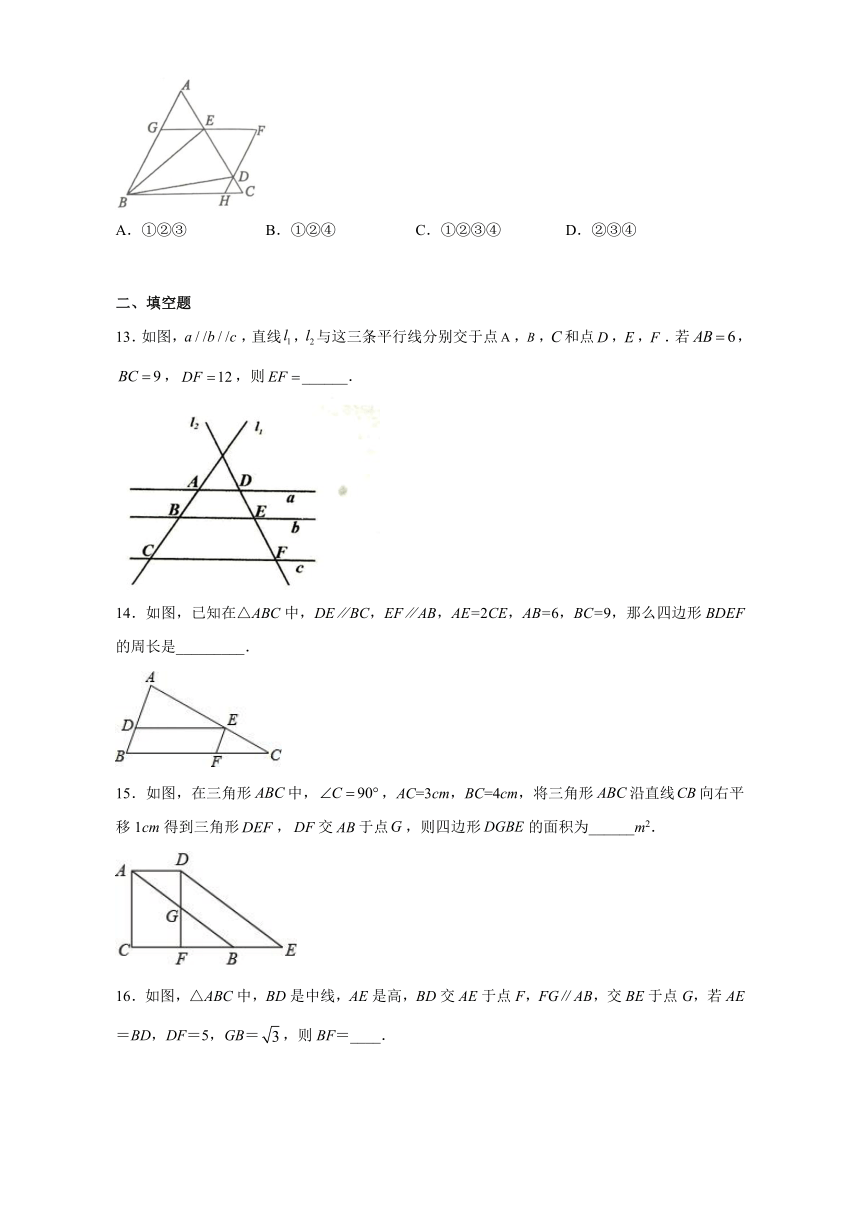
12.如图,是边长为1的等边三角形,D、E为线段AC上两动点,且,过点D、E分别作AB、BC的平行线相交于点F,分别交BC、AB于点H、G.现有以下结论:①;②当点D与点C重合时,;③;④当时,四边形BHFG为菱形,其中正确结论为(
)
A.①②③
B.①②④
C.①②③④
D.②③④
二、填空题
13.如图,,直线,与这三条平行线分别交于点,,和点,,.若,,,则______.
14.如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9,那么四边形BDEF的周长是_________.
15.如图,在三角形中,,AC=3cm,BC=4cm,将三角形沿直线向右平移1cm得到三角形,交于点,则四边形的面积为______m2.
16.如图,△ABC中,BD是中线,AE是高,BD交AE于点F,FG∥AB,交BE于点G,若AE=BD,DF=5,GB=,则BF=____.
17.如图,在正方形中,,连接,,点是的中点,连接、,点是上一点,且,过点作于点,连接,则的长为__________.
三、解答题
18.如图,已知,,求、的长.
19.如图,在△ABC中,点D,E分别在BC、AC上,BE平分ABC,DE∥BA,如果CE=24,AE=26,AB=45,求DE和CD的长.
20.如图,AD平分,过点D作于点M,的延长线于点N,且.
(1)求证:.
(2)若,求BD的长.
参考答案
1.D
解:∵,
∴,
∵,
∴,
∴AB+BC=3BC,
∴AB=2BC,
∴,
∵,
∴,
∴,
经检验符合题意.
故选择D.
2.B
解:∵AB∥CD,
∴;
∵AO=2,CO=6,BO=3,
∴,
解得:DO=4,
故选B.
3.D
解:∵,,∴,
∵,AB=5,
∴,
∴.
故选D.
4.B
解:∵AM∥BN,
∴,
又∵MC∥ND,
∴,
故选B.
5.A
解:∵DE∥BC,
∴,,
∵EF∥AB,
∴,,
∴即,
故选A.
6.C
解:∵ab,AB=1,BC=2,DE=1.8,
∴,
∴,
解得:AD=0.9,
∴AE=AD+DE=0.9+1.8=2.7,
故选:C.
7.B
解:∵DE∥BC,
∴,
∵AD=20cm,BD=12cm,CE=9cm,
∴,
∴AE=15cm,
故选:B.
8.C
解:∵DF=10,
∴ED=12﹣FE,
∵a∥b∥c,
∴=,即:,
解得:FE=6,
故选:C.
9.D
解:设
四边形ABCD为正方形
,
四边形EFGH是平行四边形
HG=EF,
,
在和中
,
同理可证明
S△BGH=S△DEF,S△AGF=S△CEH
即
S平行四边形EFGH=
故选D.
10.C
解:∵GEBD
∴,故A错误;
∵GFAC
∴,故B错误;
∵GEBD、GFAC,
∴,,
∴,故C正确;
∵
故D错误;
故选:C.
11.C
解:∵交GA于点E,
,,,,
所以,A,B,D正确,
故选:C.
12.B
解:如图1,
过A作AI⊥BC垂足为I
∵是边长为1的等边三角形
∴∠BAC=∠ABC=∠C=60°,CI=
∴AI=
∴S△ABC=,故①正确;
如图2,当D与C重合时
∵∠DBE=30°,是等边三角形
∴∠DBE=∠ABE=30°
∴DE=AE=
∵GE//BD
∴
∴BG=
∵GF//BD,BG//DF
∴HF=BG=,故②正确;
如图3,将△BCD绕B点逆时针旋转60°得到△ABN
∴∠1=∠2,∠5=∠6=60°,AN=CD,BD=BN
∵∠3=30°
∴∠2+∠4=∠1+∠4=30°
∴∠NBE=∠3=30°
又∵BD=BN,BE=BE
∴△NBE≌△DBE(SAS)
∴NE=DE
延长EA到P使AP=CD=AN
∵∠NAP=180°-60°-60°=60°
∴△ANP为等边三角形
∴∠P=60°,NP=AP=CD
如果AE+CD=DE成立,则PE=NE,需∠NEP=90°,但∠NEP不一定为90°,故③不成立;
如图1,当AE=CD时,
∵GE//BC
∴∠AGE=∠ABC=60°,∠GEA=∠C=60°
∴∠AGE=∠AEG=60°,
∴AG=AE
同理:CH=CD
∴AG=CH
∵BG//FH,GF//BH
∴四边形BHFG是平行四边形
∵BG=BH
∴四边形BHFG为菱形,故④正确.
故选B.
13.7.2
解:∵AD∥BE∥CF,
∴,即,
解得:EF=7.2,
故答案为:7.2.
14.16
解:
,
∵AB=6,BC=9,
,
∴
∵DE∥BC,EF∥AB,
∴,
四边形BDEF的周长是2+2+6+6=16;
故答案为:16.
15.
解:由平移的性质,则△ABC≌△DEF;
∴,
∴;
由平移的性质,则,AC∥DF,
∵AC=3cm,BC=4cm,
∴,
∵AC//DF,
∴
∴,即,
∴;
∴
=;
故答案为:.
16..
解:过点D作DH⊥BC于点H.
∵AE是高,
∴DH∥AE,
∵BD是中线,即D为AC中点,
∴H为BC中点,
∴DH为△CEA中位线,
∴DH=AE,
∵AE=BD,
∴DH=BD,
∴∠DBH=30°,
设BF=x,则BD=5+x,AE=5+x,
∴EF=x,BE=.
∵FG∥AB,
∴,
∴.
整理得x2+6x﹣20=0,
解得x1=,x2=(舍去).
∴BF=.
故答案为:.
17.
解:∵四边形ABCD是正方形,且AE=DE=1,
∴∠A=∠ABC=∠BCD=∠CDA=90°,AB=BC=CD=DA,AD∥BC,
∵AE=DE=1,
∴AB=BC=CD=DA=2,
过点F作FG⊥AD于G,FG交BC于H.
∵AD∥BC,FG⊥AD,
∴GH⊥BC,
∴四边形GHCD为矩形,
∴GH=CD,GD=HC,
∵FG∥CD,点F是CE的中点,
∴EG=DG=DE==HC,
GF=CD=1=FH,
∴BH=BC-HC=2-,
∵MF=2BM,
∴,
∵MN⊥BC,FH⊥AD,
∴MN∥FH,
∴,
∴BN=BH=,
∴NH=BH-BN=1,
∴NF=,
故答案为:.
18.,.
解:∵
∴,
∴,
∴,
∴,,
设,
∴,
解得.
∴.
19.,
解:∵DE∥BA,
即
∵DE∥BA,
∴∠ABE=∠DEB.
∵BE平分∠ABC,
∴∠ABE=∠DBE,
∴∠DBE=∠DEB,
∵DE∥BA,
即
20.(1)证明见解析;(2)6.
解:(1)∵AD平分,,,
∴,,
又∵,
∴,
∴
(2)∵
∴
又∵,
∴
∴是等腰直角三角形,
∴
∵
∴,
即有:.
一、单选题
1.如图,直线,那么的值是(
)
A.
B.1
C.
D.2
2.如图,已知,那么(
)
A.3
B.4
C.5
D.6
3.如图,直线,直线分别交、、于点A、B、C,直线分别交、、于点D、E、F,与相交于点H,如果,那么的值等于(
)
A.
B.
C.
D.
4.如图,在的边上任取两点B,C,过B作的平行线交于N,过N作的平行线交于D.若,则的值为(
).
A.
B.
C.2
D.3
5.如图,;;下列比例式正确的是(
).
A.
B.
C.
D.
6.如图,已知ab,另外两条直线交于点A,并与这两条平行线分别交于点B、C和D、E,若AB=1,BC=2,DE=1.8,则AE的值为( )
A.0.9
B.1.8
C.2.7
D.3.6
7.如图,在ABC中,D,E分别是AB,AC上的点,且DE∥BC.若AD=20cm,BD=12cm,CE=9cm,那么AE的长是(
)
A.13cm
B.15cm
C.16cm
D.18cm
8.如图,直线,直线,与这三条平行线分别交于点,,和点,,.若,,则(
)
A.4
B.4.5
C.6
D.5
9.如图,正方形的边,上各有一个点,,连结,且,点,,分别在,,边上,连结,,,,其中与相交于点,,为求出平行四边形的面积,只需知道下列哪条边的长度(
)
A.
B.
C.
D.
10.如图:在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GEBD,且交AB于点E,GFAC,且交CD于点F,则下列结论一定正确的是(
)
A.
B.
C.
D.
11.如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论错误的是(
)
A.
B.
C.
D.
12.如图,是边长为1的等边三角形,D、E为线段AC上两动点,且,过点D、E分别作AB、BC的平行线相交于点F,分别交BC、AB于点H、G.现有以下结论:①;②当点D与点C重合时,;③;④当时,四边形BHFG为菱形,其中正确结论为(
)
A.①②③
B.①②④
C.①②③④
D.②③④
二、填空题
13.如图,,直线,与这三条平行线分别交于点,,和点,,.若,,,则______.
14.如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9,那么四边形BDEF的周长是_________.
15.如图,在三角形中,,AC=3cm,BC=4cm,将三角形沿直线向右平移1cm得到三角形,交于点,则四边形的面积为______m2.
16.如图,△ABC中,BD是中线,AE是高,BD交AE于点F,FG∥AB,交BE于点G,若AE=BD,DF=5,GB=,则BF=____.
17.如图,在正方形中,,连接,,点是的中点,连接、,点是上一点,且,过点作于点,连接,则的长为__________.
三、解答题
18.如图,已知,,求、的长.
19.如图,在△ABC中,点D,E分别在BC、AC上,BE平分ABC,DE∥BA,如果CE=24,AE=26,AB=45,求DE和CD的长.
20.如图,AD平分,过点D作于点M,的延长线于点N,且.
(1)求证:.
(2)若,求BD的长.
参考答案
1.D
解:∵,
∴,
∵,
∴,
∴AB+BC=3BC,
∴AB=2BC,
∴,
∵,
∴,
∴,
经检验符合题意.
故选择D.
2.B
解:∵AB∥CD,
∴;
∵AO=2,CO=6,BO=3,
∴,
解得:DO=4,
故选B.
3.D
解:∵,,∴,
∵,AB=5,
∴,
∴.
故选D.
4.B
解:∵AM∥BN,
∴,
又∵MC∥ND,
∴,
故选B.
5.A
解:∵DE∥BC,
∴,,
∵EF∥AB,
∴,,
∴即,
故选A.
6.C
解:∵ab,AB=1,BC=2,DE=1.8,
∴,
∴,
解得:AD=0.9,
∴AE=AD+DE=0.9+1.8=2.7,
故选:C.
7.B
解:∵DE∥BC,
∴,
∵AD=20cm,BD=12cm,CE=9cm,
∴,
∴AE=15cm,
故选:B.
8.C
解:∵DF=10,
∴ED=12﹣FE,
∵a∥b∥c,
∴=,即:,
解得:FE=6,
故选:C.
9.D
解:设
四边形ABCD为正方形
,
四边形EFGH是平行四边形
HG=EF,
,
在和中
,
同理可证明
S△BGH=S△DEF,S△AGF=S△CEH
即
S平行四边形EFGH=
故选D.
10.C
解:∵GEBD
∴,故A错误;
∵GFAC
∴,故B错误;
∵GEBD、GFAC,
∴,,
∴,故C正确;
∵
故D错误;
故选:C.
11.C
解:∵交GA于点E,
,,,,
所以,A,B,D正确,
故选:C.
12.B
解:如图1,
过A作AI⊥BC垂足为I
∵是边长为1的等边三角形
∴∠BAC=∠ABC=∠C=60°,CI=
∴AI=
∴S△ABC=,故①正确;
如图2,当D与C重合时
∵∠DBE=30°,是等边三角形
∴∠DBE=∠ABE=30°
∴DE=AE=
∵GE//BD
∴
∴BG=
∵GF//BD,BG//DF
∴HF=BG=,故②正确;
如图3,将△BCD绕B点逆时针旋转60°得到△ABN
∴∠1=∠2,∠5=∠6=60°,AN=CD,BD=BN
∵∠3=30°
∴∠2+∠4=∠1+∠4=30°
∴∠NBE=∠3=30°
又∵BD=BN,BE=BE
∴△NBE≌△DBE(SAS)
∴NE=DE
延长EA到P使AP=CD=AN
∵∠NAP=180°-60°-60°=60°
∴△ANP为等边三角形
∴∠P=60°,NP=AP=CD
如果AE+CD=DE成立,则PE=NE,需∠NEP=90°,但∠NEP不一定为90°,故③不成立;
如图1,当AE=CD时,
∵GE//BC
∴∠AGE=∠ABC=60°,∠GEA=∠C=60°
∴∠AGE=∠AEG=60°,
∴AG=AE
同理:CH=CD
∴AG=CH
∵BG//FH,GF//BH
∴四边形BHFG是平行四边形
∵BG=BH
∴四边形BHFG为菱形,故④正确.
故选B.
13.7.2
解:∵AD∥BE∥CF,
∴,即,
解得:EF=7.2,
故答案为:7.2.
14.16
解:
,
∵AB=6,BC=9,
,
∴
∵DE∥BC,EF∥AB,
∴,
四边形BDEF的周长是2+2+6+6=16;
故答案为:16.
15.
解:由平移的性质,则△ABC≌△DEF;
∴,
∴;
由平移的性质,则,AC∥DF,
∵AC=3cm,BC=4cm,
∴,
∵AC//DF,
∴
∴,即,
∴;
∴
=;
故答案为:.
16..
解:过点D作DH⊥BC于点H.
∵AE是高,
∴DH∥AE,
∵BD是中线,即D为AC中点,
∴H为BC中点,
∴DH为△CEA中位线,
∴DH=AE,
∵AE=BD,
∴DH=BD,
∴∠DBH=30°,
设BF=x,则BD=5+x,AE=5+x,
∴EF=x,BE=.
∵FG∥AB,
∴,
∴.
整理得x2+6x﹣20=0,
解得x1=,x2=(舍去).
∴BF=.
故答案为:.
17.
解:∵四边形ABCD是正方形,且AE=DE=1,
∴∠A=∠ABC=∠BCD=∠CDA=90°,AB=BC=CD=DA,AD∥BC,
∵AE=DE=1,
∴AB=BC=CD=DA=2,
过点F作FG⊥AD于G,FG交BC于H.
∵AD∥BC,FG⊥AD,
∴GH⊥BC,
∴四边形GHCD为矩形,
∴GH=CD,GD=HC,
∵FG∥CD,点F是CE的中点,
∴EG=DG=DE==HC,
GF=CD=1=FH,
∴BH=BC-HC=2-,
∵MF=2BM,
∴,
∵MN⊥BC,FH⊥AD,
∴MN∥FH,
∴,
∴BN=BH=,
∴NH=BH-BN=1,
∴NF=,
故答案为:.
18.,.
解:∵
∴,
∴,
∴,
∴,,
设,
∴,
解得.
∴.
19.,
解:∵DE∥BA,
即
∵DE∥BA,
∴∠ABE=∠DEB.
∵BE平分∠ABC,
∴∠ABE=∠DBE,
∴∠DBE=∠DEB,
∵DE∥BA,
即
20.(1)证明见解析;(2)6.
解:(1)∵AD平分,,,
∴,,
又∵,
∴,
∴
(2)∵
∴
又∵,
∴
∴是等腰直角三角形,
∴
∵
∴,
即有:.
