3.2.1单调性与最大(小)值(第3课时)课件(共21张PPT)2021-2022学年高一上学期 人教A版(2019)数学必修第一册
文档属性
| 名称 | 3.2.1单调性与最大(小)值(第3课时)课件(共21张PPT)2021-2022学年高一上学期 人教A版(2019)数学必修第一册 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 10:35:53 | ||
图片预览








文档简介
(共21张PPT)
3.2
函数的基本性质
3.2.1单调性与最大(小)值
第3课时
回顾与引入
1.
什么是函数的单调性?什么是单调递增,单调递减,增函数、减函数?
2.理解函数的单调性时应把握好哪一些问题?
3.如何判定函数的单调性?
(1)图象法:
(2)定义法:
观察右图可以发现,二次函数f(x)=x2的图象有一个最低点(0,0),即?x∈R,都有f(x)≥f(0).
当一个函数的图象有最低点时,我们就说函数f(x)有最小值。
函数的的最大值和最小值与函数的单调性有密切的关系,通常,知道了函数的单调性就能很方便地找到函数的最值。
探究新知(一)
思考1:你能以f(x)=-x2的为例,说明函数f(x)最大值的含义吗?
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)?x?I,都有f(x)≤M;
(2)?x0?I,使得f(x0)=M.
那么,我们则称M是函数y=f(x)的最大值(maximum
value)
函数y=f(x)的最大值可用”ymax”来表示
从图象上看,函数f(x)=-x2最大的函数值为0,对应的点是图象的最高点(0,0)。
这其中有两层含义:
(1)0是f(x)=-x2的函数值,即0=f(0);
(2)0是f(x)=-x2函数值中最大的一个,即?x∈R,都有f(x)≤f(0).
函数的最大值
M大于或等于y=f(x)的任意函数值
M本身是y=f(x)的一个函数值
思考2:你能仿照函数最大值的
定义,给函数y=f(x)的最小值下定义吗?
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)?x?I,都有f(x)≥M;
(2)?x0?I,使得f(x0)=M.
那么,我们则称M是函数y=f(x)的最小值(minimum
value)
函数y=f(x)的最小值可用”ymin”来表示
函数的最小值
练习:
设函数f(x)的定义域为[-6,11],如何函数f(x)的在[-6,-2]上单调递减,在[-2,11]上单调递增,试画出f(x)的大致图象,从图象上可以发现f(2)是函数f(x)的一个__________.
x
O
-6
-2
11
f(2)
最大值
思考3:举例说明一个函数是否一定有最大值或最小值?
无最小值和最大值
有最小值,无最大值
有最小值,无最大值
(4)
y=2,x∈(1.2)
有最小值和最大值
∴烟花冲出后1.5秒是它爆裂的最佳时刻,这时距地面的高度为29
m.
例1.“菊花”烟花是最壮观的烟花之一.
制造时一般是期望在它达到最高点时爆裂.
如果烟花距地面的高度h(单位:
m)与时间t单位:
s)
之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?
例
析
作出函数h(t)=-4.9t2+14.7t+18的图象,如下图.
由图象知函数图象的顶点就是烟花上升的最高点。
顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
解:
由二次函数的知识可知,
对于h(t)=-4.9t2+14.7t+18有
解:
由二次的知识可知,
函数y=x2-2x-1的图象开口
其对称轴为
x=1
∴y=x2-2x-1的大致图象为
(1)
∵x∈[0,
3]
∴当x=1时,
ymin=12-2-1=-2
当x=3时,
ymax=32-2×3-1=2
(2)
∵x∈[2,
4]
∴当x=2时,
ymin=22-2×2-1=-1
当x=4时,
ymax=42-2×4-1=7
(3)
∵x∈[-2,
-1]
∴当x=-1时,
ymin=(-1)2-2×(-1)-1=2
当x=3时,
ymax=(-2)2-2×(-2)-1=7
例2.求定义在下列区间的函数y=x2-2x-1在的最大值和最小值.
(1)x∈[0,
3]
;
(2)
x∈(2,
4]
;
(3)
x∈[-2,
-1]
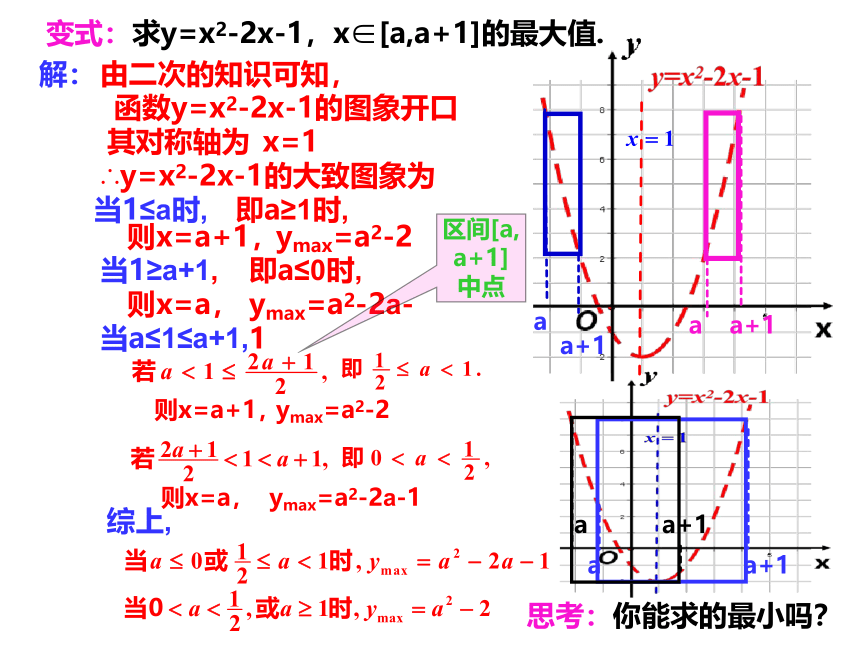
变式:求y=x2-2x-1,x∈[a,a+1]的最大值.
解:
由二次的知识可知,
函数y=x2-2x-1的图象开口
其对称轴为
x=1
∴y=x2-2x-1的大致图象为
当1≥a+1,
则x=a,
ymax=a2-2a-1
即a≤0时,
当1≤a时,
则x=a+1,
ymax=a2-2
a
a+1
a
a+1
当a≤1≤a+1,
a
a+1
则x=a+1,
ymax=a2-2
则x=a,
ymax=a2-2a-1
a
a+1
综上,
即a≥1时,
思考:你能求的最小吗?
区间[a,a+1]中点
直接利用函数图象求函数的最大(小)值主要有两种情况:
1.函数图象已知;
2.函数图象比较容易画出。
比如一些与一次函数,二次函数,反比例函数等有关的图象。
在利用二次函数的图象求它区间上的最值时,要特别注意抛物线的对称轴与区间端点的位置关系,若不确定,应进行分类讨论,一般分三种情况:对称轴在区间左,区间内和区间右。
实际上,在利用函数的图象求函数的最值有时也要结合函数的单调性。
函数最值的求法一
——
图象法
练
习
1.整个上午(8:00~12:00)天气越来越暖,中午时分(12:00~13:00)一场暴风雨使天气骤然凉爽了许多,过后,天气转暖,直到太阳落山(18:00)才又开始转凉。请画出这一天(8:00~20:00)气温关于时间的函数的大致图象,并说出所画函数的单调区间。
解:
函数的递增区间有:
[8,12],
[13,18];
函数的递减区间有:
[12,13],
[18,20]。
解:
2.求画出函数y=|x+1|-|1-x|的大致图象
,并求出函数的最大值和最小值。
当x<-1时,
y=-(x+1)-(1-x)
=-2
当-1≤x≤1时,
y=(x+1)-(1-x)
=2x
当x>1时,
y=(x+1)-[-(1-x)]
=2
∴
ymin=-2,
ymax=2
函数
y=|x+1|-|1-x|的定义域为R被-1和1分成了三段
由x+1=0和1-x=0分别得
x=-1和x=1别
综上,
其图象如右
x
y
-1
1
2
-2
o
3.在已知函数f(x)=-2x2+mx,在(-∞,-2]上递增,在[2,+∞)上递增,则m的值为________,f(x)在[-5,2]上的值域____________.
[-24,8]
-8
简析:
∵函数f(x)在(-∞,-2]上递增,在[2,+∞)上递减
y
x
O
-5
2
-2
?x1,
x2∈[2,6],
且x1由x1,
x2∈[2,6],
x1例
析
解:
x2-x1>0,(x1-1)(x2-1)>0
函数单调递减的性质可知,函数在区间[2,6]上的两个端点上分别取得最大值和最小值.
思考:此函数的图象容易画出吗?你能判定其单调性吗?
例4.求函数
的最小值。
例4.求函数
有最小值。
解:
单调性法是求函数的最大(小)值最主要的方法,在应用时要注意:
1.若函数在区间上具有单调性,则函数在区间端点处取得最值;
2.若函数在区间上不具有单调性,则应根据具体情况来求函数的最值。
如函数是先增后减,还是先减后增,函数在区间两端点处函数值的谁大谁小等。
实际上,在利用函数的单调性求最值时往往要结合函数的图象。
函数最值的求法二
——
单调性法
练习
解:
简析:
思路一:
思路二:
单调性法
不等式法
这种变形称为常数分离法
1.函数的最大(小)值的应满足哪两个条件?
其几何意义是怎样的?
小结
2.如何求一个函数的最大(小)值?
(2)图象法.
先画出函数的图象,再直接函数最值的几何意义利求函数的最大(小)值.
(1)单调性法.
先研究函数的单调性,再利用单调性的意义求函数的最大(小)值;
需要说明的是,在实际运用中,我们更多的是将这两种方法结合起来,即采用”单调性+图象”的方法。
(3)不等式法.
对于一些特殊的函数,也可以运用不等式的知识(如不等式的性质和基本不等式)来求其最值。
注意:
对于单调性不清楚的函数,不能直接把区间端点的函数值作为函数的最大(小)值
3.说说如何求一个二次函数在闭区间的最大(小)值?
首先明确二次函数图象的开口方向,对称轴,以及函数的单调性。
再找出图象在区间内的最高点,最低点。
若对称轴与区间端点的位置关系不确定,应进行分类讨论,一般分三种情况:对称轴在区间左,区间内和区间右。
4.本小节(3.2.1)的知识结构图?
单调性与最大(小)值
单调性
概念
图象特征
最大(小)值
判定
概念及几何意义
求法
作
业
1.教材P86习题3.2
第6,
7
10题
2.求函数f(x)=-4x2+4ax-4a-a2,x∈[0,1]的最大值.
布置作业
作业:课本39页A组第1、2、3题
3.2
函数的基本性质
3.2.1单调性与最大(小)值
第3课时
回顾与引入
1.
什么是函数的单调性?什么是单调递增,单调递减,增函数、减函数?
2.理解函数的单调性时应把握好哪一些问题?
3.如何判定函数的单调性?
(1)图象法:
(2)定义法:
观察右图可以发现,二次函数f(x)=x2的图象有一个最低点(0,0),即?x∈R,都有f(x)≥f(0).
当一个函数的图象有最低点时,我们就说函数f(x)有最小值。
函数的的最大值和最小值与函数的单调性有密切的关系,通常,知道了函数的单调性就能很方便地找到函数的最值。
探究新知(一)
思考1:你能以f(x)=-x2的为例,说明函数f(x)最大值的含义吗?
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)?x?I,都有f(x)≤M;
(2)?x0?I,使得f(x0)=M.
那么,我们则称M是函数y=f(x)的最大值(maximum
value)
函数y=f(x)的最大值可用”ymax”来表示
从图象上看,函数f(x)=-x2最大的函数值为0,对应的点是图象的最高点(0,0)。
这其中有两层含义:
(1)0是f(x)=-x2的函数值,即0=f(0);
(2)0是f(x)=-x2函数值中最大的一个,即?x∈R,都有f(x)≤f(0).
函数的最大值
M大于或等于y=f(x)的任意函数值
M本身是y=f(x)的一个函数值
思考2:你能仿照函数最大值的
定义,给函数y=f(x)的最小值下定义吗?
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)?x?I,都有f(x)≥M;
(2)?x0?I,使得f(x0)=M.
那么,我们则称M是函数y=f(x)的最小值(minimum
value)
函数y=f(x)的最小值可用”ymin”来表示
函数的最小值
练习:
设函数f(x)的定义域为[-6,11],如何函数f(x)的在[-6,-2]上单调递减,在[-2,11]上单调递增,试画出f(x)的大致图象,从图象上可以发现f(2)是函数f(x)的一个__________.
x
O
-6
-2
11
f(2)
最大值
思考3:举例说明一个函数是否一定有最大值或最小值?
无最小值和最大值
有最小值,无最大值
有最小值,无最大值
(4)
y=2,x∈(1.2)
有最小值和最大值
∴烟花冲出后1.5秒是它爆裂的最佳时刻,这时距地面的高度为29
m.
例1.“菊花”烟花是最壮观的烟花之一.
制造时一般是期望在它达到最高点时爆裂.
如果烟花距地面的高度h(单位:
m)与时间t单位:
s)
之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?
例
析
作出函数h(t)=-4.9t2+14.7t+18的图象,如下图.
由图象知函数图象的顶点就是烟花上升的最高点。
顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
解:
由二次函数的知识可知,
对于h(t)=-4.9t2+14.7t+18有
解:
由二次的知识可知,
函数y=x2-2x-1的图象开口
其对称轴为
x=1
∴y=x2-2x-1的大致图象为
(1)
∵x∈[0,
3]
∴当x=1时,
ymin=12-2-1=-2
当x=3时,
ymax=32-2×3-1=2
(2)
∵x∈[2,
4]
∴当x=2时,
ymin=22-2×2-1=-1
当x=4时,
ymax=42-2×4-1=7
(3)
∵x∈[-2,
-1]
∴当x=-1时,
ymin=(-1)2-2×(-1)-1=2
当x=3时,
ymax=(-2)2-2×(-2)-1=7
例2.求定义在下列区间的函数y=x2-2x-1在的最大值和最小值.
(1)x∈[0,
3]
;
(2)
x∈(2,
4]
;
(3)
x∈[-2,
-1]
变式:求y=x2-2x-1,x∈[a,a+1]的最大值.
解:
由二次的知识可知,
函数y=x2-2x-1的图象开口
其对称轴为
x=1
∴y=x2-2x-1的大致图象为
当1≥a+1,
则x=a,
ymax=a2-2a-1
即a≤0时,
当1≤a时,
则x=a+1,
ymax=a2-2
a
a+1
a
a+1
当a≤1≤a+1,
a
a+1
则x=a+1,
ymax=a2-2
则x=a,
ymax=a2-2a-1
a
a+1
综上,
即a≥1时,
思考:你能求的最小吗?
区间[a,a+1]中点
直接利用函数图象求函数的最大(小)值主要有两种情况:
1.函数图象已知;
2.函数图象比较容易画出。
比如一些与一次函数,二次函数,反比例函数等有关的图象。
在利用二次函数的图象求它区间上的最值时,要特别注意抛物线的对称轴与区间端点的位置关系,若不确定,应进行分类讨论,一般分三种情况:对称轴在区间左,区间内和区间右。
实际上,在利用函数的图象求函数的最值有时也要结合函数的单调性。
函数最值的求法一
——
图象法
练
习
1.整个上午(8:00~12:00)天气越来越暖,中午时分(12:00~13:00)一场暴风雨使天气骤然凉爽了许多,过后,天气转暖,直到太阳落山(18:00)才又开始转凉。请画出这一天(8:00~20:00)气温关于时间的函数的大致图象,并说出所画函数的单调区间。
解:
函数的递增区间有:
[8,12],
[13,18];
函数的递减区间有:
[12,13],
[18,20]。
解:
2.求画出函数y=|x+1|-|1-x|的大致图象
,并求出函数的最大值和最小值。
当x<-1时,
y=-(x+1)-(1-x)
=-2
当-1≤x≤1时,
y=(x+1)-(1-x)
=2x
当x>1时,
y=(x+1)-[-(1-x)]
=2
∴
ymin=-2,
ymax=2
函数
y=|x+1|-|1-x|的定义域为R被-1和1分成了三段
由x+1=0和1-x=0分别得
x=-1和x=1别
综上,
其图象如右
x
y
-1
1
2
-2
o
3.在已知函数f(x)=-2x2+mx,在(-∞,-2]上递增,在[2,+∞)上递增,则m的值为________,f(x)在[-5,2]上的值域____________.
[-24,8]
-8
简析:
∵函数f(x)在(-∞,-2]上递增,在[2,+∞)上递减
y
x
O
-5
2
-2
?x1,
x2∈[2,6],
且x1
x2∈[2,6],
x1
析
解:
x2-x1>0,(x1-1)(x2-1)>0
函数单调递减的性质可知,函数在区间[2,6]上的两个端点上分别取得最大值和最小值.
思考:此函数的图象容易画出吗?你能判定其单调性吗?
例4.求函数
的最小值。
例4.求函数
有最小值。
解:
单调性法是求函数的最大(小)值最主要的方法,在应用时要注意:
1.若函数在区间上具有单调性,则函数在区间端点处取得最值;
2.若函数在区间上不具有单调性,则应根据具体情况来求函数的最值。
如函数是先增后减,还是先减后增,函数在区间两端点处函数值的谁大谁小等。
实际上,在利用函数的单调性求最值时往往要结合函数的图象。
函数最值的求法二
——
单调性法
练习
解:
简析:
思路一:
思路二:
单调性法
不等式法
这种变形称为常数分离法
1.函数的最大(小)值的应满足哪两个条件?
其几何意义是怎样的?
小结
2.如何求一个函数的最大(小)值?
(2)图象法.
先画出函数的图象,再直接函数最值的几何意义利求函数的最大(小)值.
(1)单调性法.
先研究函数的单调性,再利用单调性的意义求函数的最大(小)值;
需要说明的是,在实际运用中,我们更多的是将这两种方法结合起来,即采用”单调性+图象”的方法。
(3)不等式法.
对于一些特殊的函数,也可以运用不等式的知识(如不等式的性质和基本不等式)来求其最值。
注意:
对于单调性不清楚的函数,不能直接把区间端点的函数值作为函数的最大(小)值
3.说说如何求一个二次函数在闭区间的最大(小)值?
首先明确二次函数图象的开口方向,对称轴,以及函数的单调性。
再找出图象在区间内的最高点,最低点。
若对称轴与区间端点的位置关系不确定,应进行分类讨论,一般分三种情况:对称轴在区间左,区间内和区间右。
4.本小节(3.2.1)的知识结构图?
单调性与最大(小)值
单调性
概念
图象特征
最大(小)值
判定
概念及几何意义
求法
作
业
1.教材P86习题3.2
第6,
7
10题
2.求函数f(x)=-4x2+4ax-4a-a2,x∈[0,1]的最大值.
布置作业
作业:课本39页A组第1、2、3题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
