3.2.1单调性与最大(小)值(第1课时) 课件(共23张PPT) 2021-2022学年高一上学期 人教A版(2019)数学必修第一册
文档属性
| 名称 | 3.2.1单调性与最大(小)值(第1课时) 课件(共23张PPT) 2021-2022学年高一上学期 人教A版(2019)数学必修第一册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
3.2
函数的基本性质
3.2.1单调性与最大(小)值
第1课时
前面我们学习了函数的定义及表示方法,知道函数描述了客观世界中变量之间的一种对应关系,即函数是描述事物变化规律的数学模型,这样我们就可以通过研究函数的性质获得对客观世界中事物变化规律的认识,比如,通过研究函数值随自变量值的变化规律,就可以得到函数所刻画的现实问题的变化规律。
那么,什么是函数的性质呢?
简单的说,函数的性质就是“变化中的规律性,变化中的不变性”。
因此,我们研究函数性质,就是要学会在运动变化中发现规律。
你还记得函数表示法中图象法的特点吗?
①函数图象能直观形象地表示出函数的变化趋势;
②用图象表示函数有利于研究函数的某些性质。
因此要研究函数的性质,我们可以首先从函数图象入手。
引入
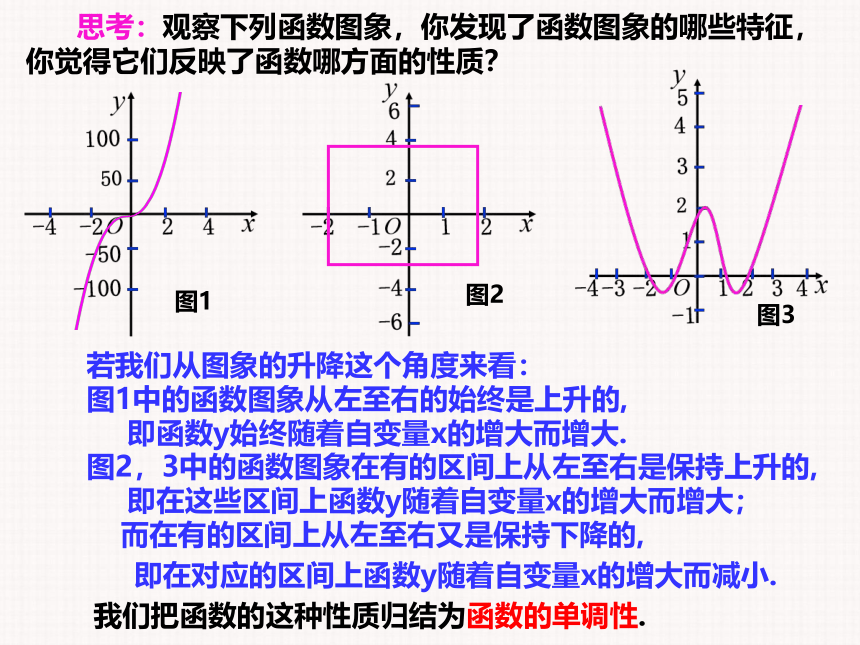
思考:观察下列函数图象,你发现了函数图象的哪些特征,你觉得它们反映了函数哪方面的性质?
若我们从图象的升降这个角度来看:
图1
图2
图3
图1中的函数图象从左至右的始终是上升的,
即函数y始终随着自变量x的增大而增大.
图2,3中的函数图象在有的区间上从左至右是保持上升的,
即在这些区间上函数y随着自变量x的增大而增大;
而在有的区间上从左至右又是保持下降的,
即在对应的区间上函数y随着自变量x的增大而减小.
我们把函数的这种性质归结为函数的单调性.
x
O
y
1
1
2
4
-1
-2
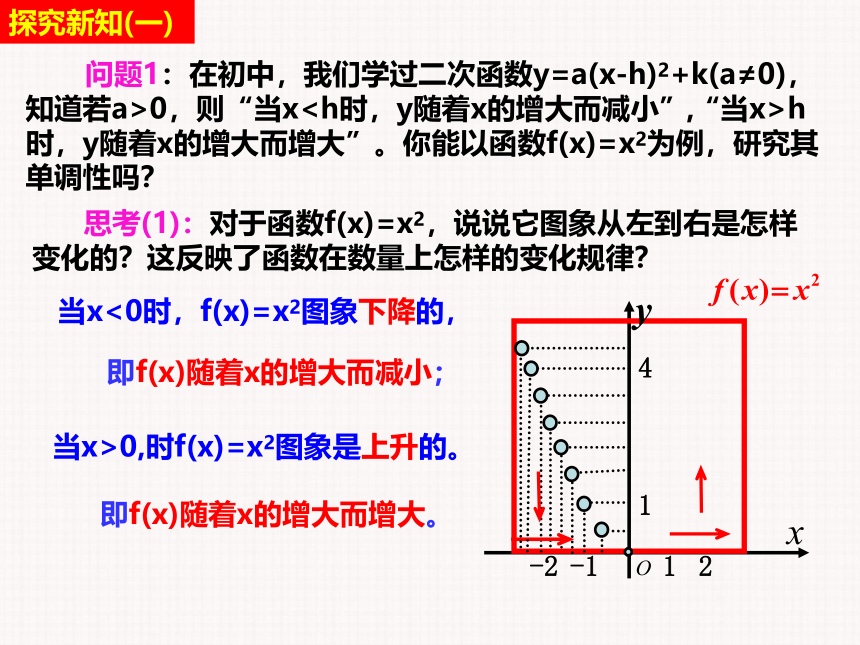
当x<0时,f(x)=x2图象下降的,
当x>0,时f(x)=x2图象是上升的。
探究新知(一)
问题1:在初中,我们学过二次函数y=a(x-h)2+k(a≠0),知道若a>0,则“当xh时,y随着x的增大而增大”。你能以函数f(x)=x2为例,研究其单调性吗?
即f(x)随着x的增大而减小;
即f(x)随着x的增大而增大。
思考(1):对于函数f(x)=x2,说说它图象从左到右是怎样变化的?这反映了函数在数量上怎样的变化规律?
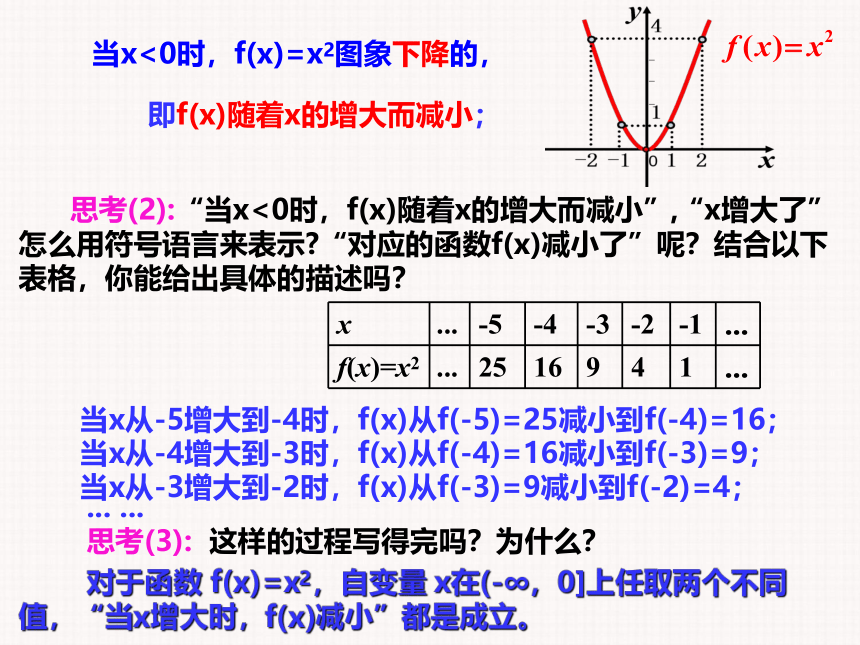
当x<0时,f(x)=x2图象下降的,
思考(2):“当x<0时,f(x)随着x的增大而减小”,“x增大了”怎么用符号语言来表示?“对应的函数f(x)减小了”呢?结合以下表格,你能给出具体的描述吗?
x
...
-5
-4
-3
-2
-1
...
f(x)=x2
...
25
16
9
4
1
...
当x从-5增大到-4时,f(x)从f(-5)=25减小到f(-4)=16;
即f(x)随着x的增大而减小;
当x从-4增大到-3时,f(x)从f(-4)=16减小到f(-3)=9;
当x从-3增大到-2时,f(x)从f(-3)=9减小到f(-2)=4;
...
...
思考(3):
这样的过程写得完吗?为什么?
对于函数
f(x)=x2,自变量
x在(-∞,0]上任取两个不同值,“当x增大时,f(x)减小”都是成立。
y
x
O
x2
x1
即当x<0时,
只要x1f(x2)
思考(4):
如何表述这种任意性?你能写出更严格的表达吗?
在(-∞,0]上任取
x1、x2
,只要x1f(x2),
这时我们说函数f(x)在(-∞,0]上是单调递减的。
思考(5):
对于函数f(x)=x2,你能模仿以上的方法,给出“在区间[0,+∞)上,f(x)随着x的增大而增大”的符号语言刻画吗?
在[0,+∞)上任取
x1、x2
,只要x1这时我们说函数f(x)在[0,+∞)上是单调递增的。
练习
仿照上述方法,用严格的符号语言刻画函数f(x)=|x|和y=-x2各自的单调性。
对于函数f(x)=|x|:
在(-∞,0]上,图象从左至右下降;
f(x)随着x的增大而减小;
任取
x1、x2
∈(-∞,0],当x1f(x2),
即函数f(x)在(-∞,0]上是单调递减的。
同理,任取
x1、x2
∈[0,+∞),当x1即函数f(x)在(-∞,0]上是单调递增的。
对于函数f(x)=-x2:
在(-∞,0]上,图象从左至右上升;
f(x)随着x的增大而增大;
任取
x1、x2
∈[0,+∞),当x1同理,任取
x1、x2
∈(-∞,0],当x1f(x2),即函数f(x)在(-∞,0]上是单调递减的。
单调递减和减函数
单调递增和增函数
函数的单调性
返回
问题2:(1)设A是区间D上的自变量的某些值组成的集合,而且?x1,x2∈A,当x1不能.
例如对于函数f(x)=|x|,
取区间D=(-4,4),
集合A={-1,2,3}.
则?x1,x2∈{-1,2,3},当x1但f(x)=|x|在(-4,4)上并不单调递增.
又如对于函数f(x)=-x2,
取区间D=(-10,10),
集合A=(-10,0).
则?x1,x2∈(-10,0),当x1但f(x)=x2在(-10,10)上并不单调递增。
函数的单调性是对定义域I上的某个区间D而言的,自变量在整个区间D上的取值x1和x2(x1≠x2)具有任意性。不能用自变量在区间D内某两个值来或者区间D一部分内的任意两个值x1,x2来代替。
探究新知(二)
(2)函数的单调性是对定义域上的某个区间而言的,你能举出在整个定义域内单调递增的函数吗?在定义域内的某些区间单调而在另一些区间上单调递减的函数吗?
函数f(x)=x+1在整个定义域R上单调递增,即是增函数。
函数f(x)=x2-2x在(-∞,1)单调递增,
在(1,+∞)单调递减。
y
x
O
增函数、减函数是针对的是函数的整个定义域,是函数的整体性质,而函数的单调性是对定义域下的某个区间,是函数的局部性质。
一个函数在定义域下的某个区间具有单调性,但在整个定义上不一定具有单调性。
y
x
O
它在(-∞,0)上单调递减,
在(0,+∞)上单调递减
但在定义域(-∞,0)∪(0,+∞)上不单调单调递减,即不是减函数。
一个函数在区间A和B上都具有相同的单调性,但在A∪B上不一定有这种单调性,即单调区间不能简单合并。
(4)函数单调区间的端点是取还是不取?
单调性反映的是函数f(x)随自变量x的增大而增大或减小的性质,在单个点上谈单调性没有意义。
因此,一般地,对于图象连续不断的函数,若其定义域含区间的端点,则单调区间可以取端点,也可不取不取端点。
理解函数的单调性时应把好的几个些问题
(1)函数的单调性是对定义域I上的某个区间D而言的,自变量在整个区间D上的取值x1和x2(x1≠x2)具有任意性。不能用自变量在区间D内某两个值来或者在区间D内一部分内的任意两个值x1,x2来代替。
(2)单调区间不能简单合并。一个函数在区间A和B上都具有相同的单调性,但在A∪B上不一定有这种单调性。
(3)一个函数在定义域下的某个区间具有单调性,但在整个定义上不一定具有单调性。
(4)增函数、减函数是针对的是函数的整个定义域,是函数的整体性质,而函数的单调性是对定义域下的某个区间,是函数的局部性质。
(5)一般地,对于图象连续不断的函数,若其定义域含区间的端点,则单调区间可以取端点,也可以不取端点。
单调性反映的是函数f(x)随自变量x的增大而增大或减小的性质,在单个点上谈单调性没有意义
返回
练习
请根据右图描述某装配线的生产效率与生产线上工人人数间的关系.
在一定范围内,生产效率随着工人人数的增加而提高.
当工人人数达到某个数量时,生产效率达到最大值.
当工人人数超过这个数量时,生产效率随着工人人数的增加却越来越低。
例
析
可以采取作差法,其一般步骤为:
(1)作差;
(2)变形;
目的:便于判定差的符号
常用的方法:因式分解、配方、通分、分子有理化等
(3)定号;
当差的符号不确定时,一般需要分类讨论
(4)作结论。
根据当差的正负与实数大小关系的基本事实作出结论
确定取值区间
取值
比较大小
作出结论
用定义法研究函数单调性的一般步骤
①确定取值区间D:
定义域或定义域下的某个区间
②取值:
任取x1,x2∈D,且x1③比较大小:
一般情况下,用作差法来比较f(x1)和f(x2)的大小
④作结论:
根据单调性的定义作出结论.
返回
练习
确定取值区间
取值
比较大小
作出结论
例
析
x
O
x
O
练习
1.
什么是函数的单调性?什么是单调递增,单调递减,增函数、减函数?
小结
2.理解函数的单调性时应把握好哪一些问题?
3.通过本节的学习,你认为可如何判定函数的单调性?
(1)图象法(直观判断);
(2)定义法(严格推导)。
4.通过本节的学习,你对函数性质的研究方法有什么体会?
具体函数→图象特征(定性刻画)
→数量刻画(定量刻画)
→数学符号语言
→抽象出单调性的一般定义
→判定具体函数的单调性。
作
业
教材P86习题3.2
第1,
2,
3题
布置作业
作业:课本39页A组第1、2、3题
3.2
函数的基本性质
3.2.1单调性与最大(小)值
第1课时
前面我们学习了函数的定义及表示方法,知道函数描述了客观世界中变量之间的一种对应关系,即函数是描述事物变化规律的数学模型,这样我们就可以通过研究函数的性质获得对客观世界中事物变化规律的认识,比如,通过研究函数值随自变量值的变化规律,就可以得到函数所刻画的现实问题的变化规律。
那么,什么是函数的性质呢?
简单的说,函数的性质就是“变化中的规律性,变化中的不变性”。
因此,我们研究函数性质,就是要学会在运动变化中发现规律。
你还记得函数表示法中图象法的特点吗?
①函数图象能直观形象地表示出函数的变化趋势;
②用图象表示函数有利于研究函数的某些性质。
因此要研究函数的性质,我们可以首先从函数图象入手。
引入
思考:观察下列函数图象,你发现了函数图象的哪些特征,你觉得它们反映了函数哪方面的性质?
若我们从图象的升降这个角度来看:
图1
图2
图3
图1中的函数图象从左至右的始终是上升的,
即函数y始终随着自变量x的增大而增大.
图2,3中的函数图象在有的区间上从左至右是保持上升的,
即在这些区间上函数y随着自变量x的增大而增大;
而在有的区间上从左至右又是保持下降的,
即在对应的区间上函数y随着自变量x的增大而减小.
我们把函数的这种性质归结为函数的单调性.
x
O
y
1
1
2
4
-1
-2
当x<0时,f(x)=x2图象下降的,
当x>0,时f(x)=x2图象是上升的。
探究新知(一)
问题1:在初中,我们学过二次函数y=a(x-h)2+k(a≠0),知道若a>0,则“当x
即f(x)随着x的增大而减小;
即f(x)随着x的增大而增大。
思考(1):对于函数f(x)=x2,说说它图象从左到右是怎样变化的?这反映了函数在数量上怎样的变化规律?
当x<0时,f(x)=x2图象下降的,
思考(2):“当x<0时,f(x)随着x的增大而减小”,“x增大了”怎么用符号语言来表示?“对应的函数f(x)减小了”呢?结合以下表格,你能给出具体的描述吗?
x
...
-5
-4
-3
-2
-1
...
f(x)=x2
...
25
16
9
4
1
...
当x从-5增大到-4时,f(x)从f(-5)=25减小到f(-4)=16;
即f(x)随着x的增大而减小;
当x从-4增大到-3时,f(x)从f(-4)=16减小到f(-3)=9;
当x从-3增大到-2时,f(x)从f(-3)=9减小到f(-2)=4;
...
...
思考(3):
这样的过程写得完吗?为什么?
对于函数
f(x)=x2,自变量
x在(-∞,0]上任取两个不同值,“当x增大时,f(x)减小”都是成立。
y
x
O
x2
x1
即当x<0时,
只要x1
思考(4):
如何表述这种任意性?你能写出更严格的表达吗?
在(-∞,0]上任取
x1、x2
,只要x1
这时我们说函数f(x)在(-∞,0]上是单调递减的。
思考(5):
对于函数f(x)=x2,你能模仿以上的方法,给出“在区间[0,+∞)上,f(x)随着x的增大而增大”的符号语言刻画吗?
在[0,+∞)上任取
x1、x2
,只要x1
练习
仿照上述方法,用严格的符号语言刻画函数f(x)=|x|和y=-x2各自的单调性。
对于函数f(x)=|x|:
在(-∞,0]上,图象从左至右下降;
f(x)随着x的增大而减小;
任取
x1、x2
∈(-∞,0],当x1
即函数f(x)在(-∞,0]上是单调递减的。
同理,任取
x1、x2
∈[0,+∞),当x1
对于函数f(x)=-x2:
在(-∞,0]上,图象从左至右上升;
f(x)随着x的增大而增大;
任取
x1、x2
∈[0,+∞),当x1
x1、x2
∈(-∞,0],当x1
单调递减和减函数
单调递增和增函数
函数的单调性
返回
问题2:(1)设A是区间D上的自变量的某些值组成的集合,而且?x1,x2∈A,当x1
例如对于函数f(x)=|x|,
取区间D=(-4,4),
集合A={-1,2,3}.
则?x1,x2∈{-1,2,3},当x1
又如对于函数f(x)=-x2,
取区间D=(-10,10),
集合A=(-10,0).
则?x1,x2∈(-10,0),当x1
函数的单调性是对定义域I上的某个区间D而言的,自变量在整个区间D上的取值x1和x2(x1≠x2)具有任意性。不能用自变量在区间D内某两个值来或者区间D一部分内的任意两个值x1,x2来代替。
探究新知(二)
(2)函数的单调性是对定义域上的某个区间而言的,你能举出在整个定义域内单调递增的函数吗?在定义域内的某些区间单调而在另一些区间上单调递减的函数吗?
函数f(x)=x+1在整个定义域R上单调递增,即是增函数。
函数f(x)=x2-2x在(-∞,1)单调递增,
在(1,+∞)单调递减。
y
x
O
增函数、减函数是针对的是函数的整个定义域,是函数的整体性质,而函数的单调性是对定义域下的某个区间,是函数的局部性质。
一个函数在定义域下的某个区间具有单调性,但在整个定义上不一定具有单调性。
y
x
O
它在(-∞,0)上单调递减,
在(0,+∞)上单调递减
但在定义域(-∞,0)∪(0,+∞)上不单调单调递减,即不是减函数。
一个函数在区间A和B上都具有相同的单调性,但在A∪B上不一定有这种单调性,即单调区间不能简单合并。
(4)函数单调区间的端点是取还是不取?
单调性反映的是函数f(x)随自变量x的增大而增大或减小的性质,在单个点上谈单调性没有意义。
因此,一般地,对于图象连续不断的函数,若其定义域含区间的端点,则单调区间可以取端点,也可不取不取端点。
理解函数的单调性时应把好的几个些问题
(1)函数的单调性是对定义域I上的某个区间D而言的,自变量在整个区间D上的取值x1和x2(x1≠x2)具有任意性。不能用自变量在区间D内某两个值来或者在区间D内一部分内的任意两个值x1,x2来代替。
(2)单调区间不能简单合并。一个函数在区间A和B上都具有相同的单调性,但在A∪B上不一定有这种单调性。
(3)一个函数在定义域下的某个区间具有单调性,但在整个定义上不一定具有单调性。
(4)增函数、减函数是针对的是函数的整个定义域,是函数的整体性质,而函数的单调性是对定义域下的某个区间,是函数的局部性质。
(5)一般地,对于图象连续不断的函数,若其定义域含区间的端点,则单调区间可以取端点,也可以不取端点。
单调性反映的是函数f(x)随自变量x的增大而增大或减小的性质,在单个点上谈单调性没有意义
返回
练习
请根据右图描述某装配线的生产效率与生产线上工人人数间的关系.
在一定范围内,生产效率随着工人人数的增加而提高.
当工人人数达到某个数量时,生产效率达到最大值.
当工人人数超过这个数量时,生产效率随着工人人数的增加却越来越低。
例
析
可以采取作差法,其一般步骤为:
(1)作差;
(2)变形;
目的:便于判定差的符号
常用的方法:因式分解、配方、通分、分子有理化等
(3)定号;
当差的符号不确定时,一般需要分类讨论
(4)作结论。
根据当差的正负与实数大小关系的基本事实作出结论
确定取值区间
取值
比较大小
作出结论
用定义法研究函数单调性的一般步骤
①确定取值区间D:
定义域或定义域下的某个区间
②取值:
任取x1,x2∈D,且x1
一般情况下,用作差法来比较f(x1)和f(x2)的大小
④作结论:
根据单调性的定义作出结论.
返回
练习
确定取值区间
取值
比较大小
作出结论
例
析
x
O
x
O
练习
1.
什么是函数的单调性?什么是单调递增,单调递减,增函数、减函数?
小结
2.理解函数的单调性时应把握好哪一些问题?
3.通过本节的学习,你认为可如何判定函数的单调性?
(1)图象法(直观判断);
(2)定义法(严格推导)。
4.通过本节的学习,你对函数性质的研究方法有什么体会?
具体函数→图象特征(定性刻画)
→数量刻画(定量刻画)
→数学符号语言
→抽象出单调性的一般定义
→判定具体函数的单调性。
作
业
教材P86习题3.2
第1,
2,
3题
布置作业
作业:课本39页A组第1、2、3题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
