人教版数学12.1全等三角形课件(20张ppt)
文档属性
| 名称 | 人教版数学12.1全等三角形课件(20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 14:07:24 | ||
图片预览







文档简介
(共20张PPT)
12.1
全等三角形
教学目标
1.知道什么是全等形、全等三角形及全等三角形的对应元素;
2.知道全等三角形的性质,能用符号正确地表示两个三角形全等;
3.能熟练找出两个全等三角形的对应角、对应边.
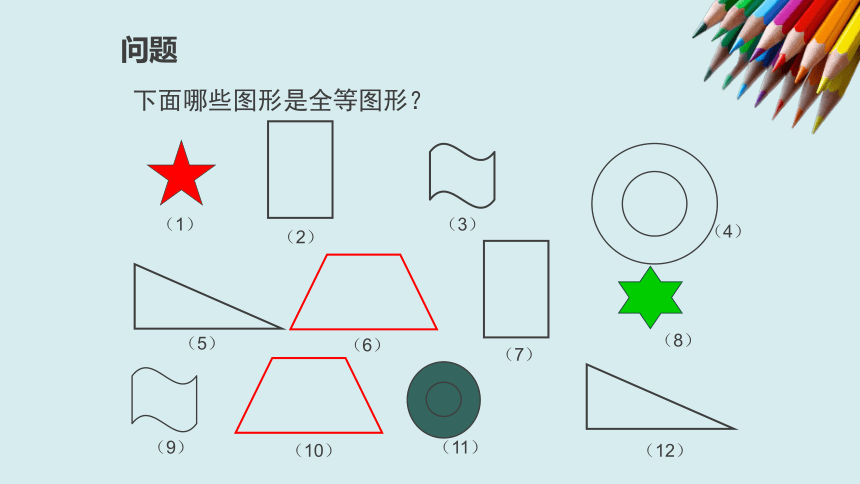
下面哪些图形是全等图形?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
问题
E
D
F
E
D
F
全等三角形的定义及性质
A
B
C
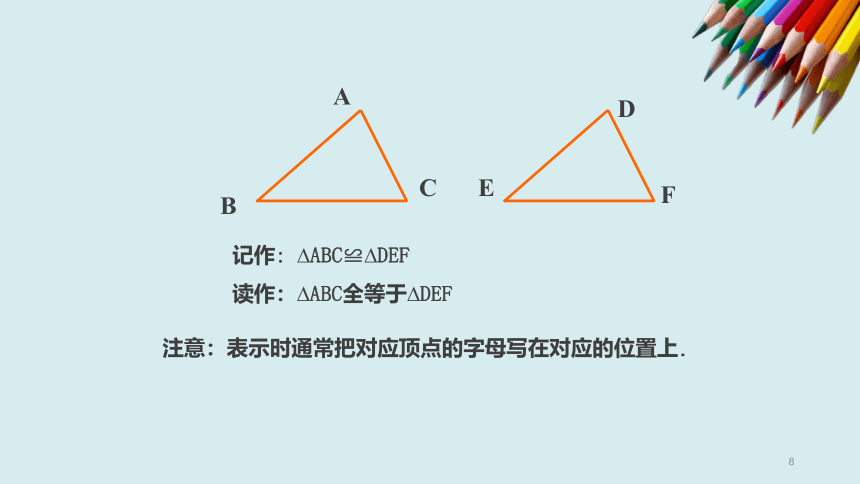
像上图一样,把△ABC叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.
把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.
例1.如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
3
4
找一找下列全等图形的对应元素?
A
B
C
D
F
A
B
C
E
D
F
∵△ABC≌△DEF(已知),
∴AB=DE,
AC=DF,BC=EF(全等三角形对
应边相等),
∠A=∠D,
∠B=∠E,
∠C=∠F(全等三角形对应角相等).
全等的性质
全等三角形的对应边相等;
全等三角形的对应角相等.
∵△ABC≌△FDE
∴A
B=F
D,A
C=F
E,B
C=D
E(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
试一试:
如图,△ABC与△ADC全等,请用数学符号表示出
这两个三角形全等,并写出相等的边和角.
解:△ABC≌△ADC;
相等的边为:AB=AD,AC=AC,BC=DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
4.如图,△ABC≌△BAD,如果AB=5cm,
BD=
4cm,AD=6cm,那么BC的长是
(
)
A.6cm
B.5cm
C.4cm
D.无法确定
5.在上题中,∠CAB的对应角是
(
)
A.∠DAB
B.∠DBA
C.∠DBC
D.∠CAD
A
O
C
D
B
A
B
6.如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
7.如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N,
∠F和∠M,
∠EGF和∠NHM.
(2)求线段NM及HG的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
解:∵
△EFG≌△NMH,
∴NM=EF=2.1cm,
EG=NH=3.3cm.
∴HG=EG
–EH=3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明:
∵
△EFG≌△NMH,
∴
∠E=∠N.
∴
EF∥NM.
1.全等(三角形)形的概念;
2.全等三角形的性质;
3.识别全等三角形的对应边、对应角.
课堂小结
12.1
全等三角形
教学目标
1.知道什么是全等形、全等三角形及全等三角形的对应元素;
2.知道全等三角形的性质,能用符号正确地表示两个三角形全等;
3.能熟练找出两个全等三角形的对应角、对应边.
下面哪些图形是全等图形?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
问题
E
D
F
E
D
F
全等三角形的定义及性质
A
B
C
像上图一样,把△ABC叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.
把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.
例1.如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
3
4
找一找下列全等图形的对应元素?
A
B
C
D
F
A
B
C
E
D
F
∵△ABC≌△DEF(已知),
∴AB=DE,
AC=DF,BC=EF(全等三角形对
应边相等),
∠A=∠D,
∠B=∠E,
∠C=∠F(全等三角形对应角相等).
全等的性质
全等三角形的对应边相等;
全等三角形的对应角相等.
∵△ABC≌△FDE
∴A
B=F
D,A
C=F
E,B
C=D
E(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
试一试:
如图,△ABC与△ADC全等,请用数学符号表示出
这两个三角形全等,并写出相等的边和角.
解:△ABC≌△ADC;
相等的边为:AB=AD,AC=AC,BC=DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
4.如图,△ABC≌△BAD,如果AB=5cm,
BD=
4cm,AD=6cm,那么BC的长是
(
)
A.6cm
B.5cm
C.4cm
D.无法确定
5.在上题中,∠CAB的对应角是
(
)
A.∠DAB
B.∠DBA
C.∠DBC
D.∠CAD
A
O
C
D
B
A
B
6.如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
7.如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N,
∠F和∠M,
∠EGF和∠NHM.
(2)求线段NM及HG的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
解:∵
△EFG≌△NMH,
∴NM=EF=2.1cm,
EG=NH=3.3cm.
∴HG=EG
–EH=3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明:
∵
△EFG≌△NMH,
∴
∠E=∠N.
∴
EF∥NM.
1.全等(三角形)形的概念;
2.全等三角形的性质;
3.识别全等三角形的对应边、对应角.
课堂小结
